Open Journal of Applied Sciences
Vol.05 No.08(2015), Article ID:58734,8 pages
10.4236/ojapps.2015.58043
A Dynamical Model to Analyze the Influence of Sliding Friction on Motion on a Curve―An Analytical Method*
Prahlad Kulkarni
Department of Mechanical Engineering, R V College of Engineering, Bangalore, India
Email: Prahlad321pk@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 July 2015; accepted 9 August 2015; published 12 August 2015
ABSTRACT
To demonstrate the influence of sliding friction of motion on a curve, a circular path is considered for simplicity on which a person slides from the highest point to the lowest point. A slide which represents a quadrant of radius 5 m and a person of mass 60 kg are considered for comparison in this paper. A Differential equation for motion considering the fact that the normal force depends both on the sin component of weight and also on the tangential velocity, is established and is solved using integrating factor method, and the motion is analysed for different surface roughness of the slide and is compared using superimposed graphs, also the limiting value of friction coefficient at which the person just exits the slide is determined. The correction factor for exit velocity with friction as compared with the exit velocity for zero friction is determined. The fraction of energy lost to friction at the exit is evaluated. The Variation of normal force with the position of the person on the slide is plotted for different surface roughness of the slide, and the position on the slide where the normal force or the force experienced by the person is maximum, is determined and hence its maximum value is evaluated for different surface roughness. For simplicity, a point contact between the body and the slide is considered.
Keywords:
Sliding Friction, Surface Roughness, Integrating Factor Method, Correction Factor, Critical Coefficient of Friction, Exit Velocity

1. Introduction
Friction put in simple words is the resistance to motion because of the contact between the body and the supporting surface. It is basically classified into two types―static and dynamic friction, static friction acts between two bodies with no relative motion with respect to each other whereas dynamic friction acts between two bodies with a relative motion with respect to each other, several attempts have been made to understand the general working of friction [1] [2] , and the dynamics of sliding friction [3] - [5] also have attempted to measure the coefficient of friction on a curved surface [6] but however, this paper concentrates on the effect of sliding friction of motion on a circular surface by choosing different values for the coefficient of friction as the initial condition. Friction force is obtained by multiplying friction coefficient and normal force acting perpendicular to the rough surface, in most cases, the normal force is either a constant or a simple function of weight, and the analysis is mostly done for motion on a straight path, but when motion on a curve-circular surface (as discussed in this paper) is considered, the analysis becomes complicated as the normal force depends both on the sin component of weight (thus it depends on the angle of inclination with horizontal) and also on the tangential velocity (which produces centrifugal force acting normally on the slide-body interface), thus it is a complex function which varies with two parameters (q, v), for which a differential equation for motion is established and solved, considering all the relevant factors.
2. Methodology
Ø First a slide which represents a quadrant of radius 5 m (for simplicity) is assumed on which the person of mass m = 60 kg slides from the top(q = 0) to the exit or the end of the slide (q = 90 degree) and the differential equation for motion is established and is solved using integrating factor method to get the variation of tangential velocity (v) with the position (q) on the slide
Ø Exit velocity(the velocity at which the person exits the slide) is determined as a function of friction coefficient (u) and is compared with the exit velocity for zero friction and a term called ‘the correction factor’ is defined which accounts for the change in exit velocity due to the presence of friction ,and another term called “critical coefficient of friction” is defined which is a limiting value of friction coefficient beyond which the person ceases to exit or come out of the slide
Ø Motion is analyzed for different surface roughness (different values of u) of the slide and a superimposed graph of v vs q is plotted to clearly show the effects of different surface roughness on the velocity profile
Ø The variation of the normal force on the person with his position on the slide is plotted and the position where the normal force is maximum and hence its value is determined for different surface roughness values of the slide
Ø Percentage of energy lost to friction is determined as a function of coefficient of friction u and a graph is plotted between the two
3. Analysis
By referring to Figure 1 consider a person sliding down a circular slide (a quadrant in this case) of radius R and the coefficient of friction between the person and the slide is u
Figure 1. Free Body Diagram (FBD).
m = mass of the person (60 kg)
q = angle of inclination with the horizontal
N = normal force
f = frictional force
u = coefficient of friction
g = acceleration due to gravity (9.81 m/s2)
v = absolute velocity of the person
R = Radius of curvature of the slide (5 m)
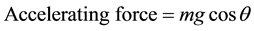 (1)
(1)
Retarding force = friction force = 
N = fn (cos component of weight, centrifugal force)
 (2)
(2)
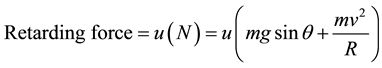 (3)
(3)
From FBD, by equilibrium of forces
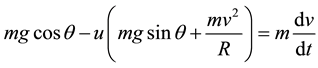 (4)
(4)
But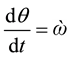 , thus
, thus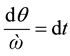 , ὼ = angular velocity
, ὼ = angular velocity
But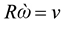 , thus,
, thus,
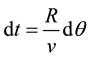 Substituting
Substituting 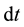 in Equation (1) we get:
in Equation (1) we get:
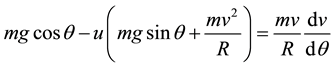
Multiplying by R and dividing by m we get:
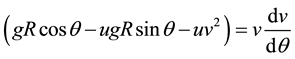
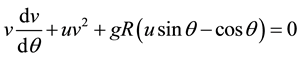 (5)
(5)
Thus Equation (5) represents the differential equation of motion on the slide
Now if we put u = 0 the equation becomes
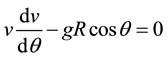
which represents the motion without friction which upon solving gives 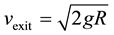 thus the differential equation obtained (5) is correct.
thus the differential equation obtained (5) is correct.
Solution:
The Equation (5) represents non-linear single order ordinary differential equation:
To solve put v2 = z
Differentiating w.r.t q,
Thus substituting in Equation (1) we get:

Now this type of differential equation can be solved by integrating factor method:
Integrating factor
Thus the solution will be:
But z = v2 thus substituting:

Now exit velocity is obtained by setting q = 90˚ or π/2 rad:

Now exit velocity without friction can be obtained by setting u=0
Thus 
Thus to consider friction effects, a correction factor f is to be multiplied,

Fraction of Energy lost to friction:


Determination of maximum normal force on the person and the location on the track (qn) where it occurs:

Now to find the maximum value of N differential of N, w r t q s
Now to find the maximum value of N differential of N, w r t q should be zero
Thus
Thus by solving the following equation:
For different values of u, different positions (qn) values for which the normal force is maximum are obtained
4. Results and Discussion
4.1. vexit vs u
Considering a case where R = 5 m, exit velocity vs u graph is plotted.
It can be inferred from Figure 2 that exit velocity rapidly decreases with increase in friction coefficient u, when u = 0, vexit = 9.9 m/s 
which gives:
After solving uc is obtained as 0.60259, thus for all practical purposes, the person comes out only if the roughness combination of his clothing and the slide surface produces a friction coefficient of less than 0.60259 (for all u < uc) A table below lists the values of exit velocity for different values of u (R = 5 m) it is to be noted that uc does not depend on any initial condition and is a characteristic of the geometry under consideration (circular surface in this case) hence uc for a circular surface is found to be 0.60259 Table 1 lists out exit velocity values for different values of the coefficient of friction u.
4.2. v vs θ
This gives the variation of absolute velocity of the person with his angular position (q) on the slide, the curves are plotted for different values of friction coefficient u of the slide surface and the graphs are compared by: superimposing
It can be inferred from the Figure 3 that as coefficient of friction u increases, the curve shifts downwards and at u = uc (critical coefficient of friction) the curve touches the x axis thus vexit will become zero and it will remain zero (the person will not come out) for all values of u > uc.
Figure 2. Variation of vexit with u.
Table 1. vexit vs u.
4.3. Variation of Normal Force with Ө
It can be inferred from Figure 4 that as coefficient of friction u between the person and the slide increases the normal force reduces as the curves shift down for higher values of u and the normal force is minimum for u = uc (critical value). Table 2 lists out the values of Nmax for different values of u and the angle at which it occurs.
4.4. F vs u
Figure 5 shows the variation of fraction of energy (F) lost at exit with friction coefficient u.
Table 3 lists out the F values (%) vs coefficient of friction (u).
Figure 3. Velocity v vs angle traversed.
Figure 4. Normal force (N) vs angle traversed.
Table 2. Tabulatıon of Nmax and qN for different u values (For mass of the person M = 60 Kg).
Figure 5. Fraction of energy lost (F) vs friction coefficient (u).
Table 3. List of F (%) values vs u.
5. Conclusion
Although this paper does not dwell into inner working of kinetic friction at the interface or molecular level, it attempts to quantify the effects of sliding friction on motion on a curve, a circular path considered in this paper, thus a dynamical model is developed to understand the motion of the person on the slide by deriving a differential equation which represents the motion, then the equation is solved by an analytical method to obtain the exact variation of velocity with time, the exit velocity is compared with different surface roughness and is compared with exit velocity for zero friction. The variation of normal force with the position on the slide is determined and is compared with different roughness, the critical coefficient of friction is determined and its implications are stated, however, the analysis can be extended to any other non-linear geometry like parabola or an exponential function.
Applications
Even though a detailed analysis is not shown in this paper, the model can be used to optimize the flight evacuation system which at present consists of a straight slide but instead if it were to be made like a circular then the motion of the passengers can be controlled and optimized by choosing a roughness value such that it lies within a close range of the critical coefficient of friction uc such that the passengers can be made to slow down and stop exactly at the end of the slide to avoid injuries caused by tripping and falling due to loss of control.
Cite this paper
PrahladKulkarni, (2015) A Dynamical Model to Analyze the Influence of Sliding Friction on Motion on a Curve—An Analytical Method. Open Journal of Applied Sciences,05,434-442. doi: 10.4236/ojapps.2015.58043
References
- 1. Curnier, A. (1984) A Theory of Friction. International Journal of Solid Structures, 20, 637-647.
- 2. Jellet, J.H. (1872) A Treatise on the Theory of Friction. Hodges Foster & Co., Leuven.
- 3. Al-Bender, F., Lampaert, V. and Swevers, J. (2002) Modelling of Dry Sliding Friction Dynamics: From Heuristic Models to Physically Motivated Models and Back. Chaos—An Interdisciplinary Journal of Nonlinear Science, 14, 446-460.
- 4. Berger, E.J. (2002) Friction Modelling for Dynamic System Simulation. Applied Mechanics Reviews, 55.
- 5. Goyal, S. (1989) Planar Sliding of a Rigid Body with Dry Friction: Limit Surfaces and Dynamics of Motion. A Dissertation Presented to the Faculty of Graduate School of Cornell University in Partial Requirements for the Degree of Doctor of Philosophy.
- 6. Wu, C.L., Yang, L.F. and He, Y.L. (2013) On the Measurement of Friction Coefficient at the Curved Surface in Metal Forming. Applied Mechanics and Materials, 446-447, 1134-1137.
NOTES
*This paper is partly based on a presentation in Proceedings of 24th IRF International Conference, 3rd May 2015, Chennai, India.

































