ABSTRACT

Pneumatic artificial muscles (PAMs) have the highest power to weight and power to volume ratios of any actuator. Therefore, they can be used not only in rehabilitation engineering, but also as actuators in robots, including industrial and therapy robots. Because PAMs have highly nonlinear and time-varying behavior associated with gas compression and the nonlinear elasticity of bladder containers, achieving excellent tracking performance using classical controllers is difficult. An adaptive self-tuning fuzzy controller (ASTFC) including adaptive fuzzy sliding mode control (AFSMC) and functional approximation (FA) was developed in this study for overcoming the aforementioned problems. The FA technique was used to release the model-based requirements and the update laws for the coefficients of the Fourier series function parameters were derived using a Lyapunov function to guarantee control system stability. The experimental results verified that the proposed approach can achieve excellent control performance despite external disturbance.

Keywords:

Adaptive Self-Tuning Fuzzy Control, Pneumatic Artificial Muscles, Functional Approximation, Lyapunov Function

1. Introduction

Rehabilitation machine provides joint loading to assist patients in recovering extremity functions in cases of traumatic brain injury, bone injury, amputation, or spinal cord injury with causes such as traffic accidents and cerebral apoplexy that affect extremity activity. Rehabilitation robots can assist patients in recovering extremity functions by means of continuous passive motion (CPM). Traditionally, physical therapy for functional rehabilitation is administered by medical therapists on a person-to-person basis. However, recently many automatic rehabilitation devices have been applied in physical therapy programs. Rehabilitation robots are typically driven by electric motors, which are typically rigid. Consequently, actuators can generate discomfort or pain when interfacing with humans. Hence, current electro-mechanical actuation systems should be replaced to ensure adaptability, conformity and safety. An adequate actuator for a rehabilitation device must provide safety and physically adjustable compliance. Additionally, it must ensure soft contact with the patient, similar to human muscles. It has been suggested that pneumatic artificial muscles (PAMs) can contribute to creating more comfortable devices for interfacing with human limb segments.

A submissive PAM consists of a cylinder of flexible rubber surrounded by a braided mesh shell. When the rubber bladder expands because of an increase in air pressure, the diameter of the combined shell and bladder assembly expands in the radial direction and the muscle retracts in the axial direction. A PAM behaves in a manner similar to a muscle on an animal skeleton, and a PAM has many advantages such as a high power to weight ratio [1] , high power to volume ratio [2] , low maintenance expense, no mechanical wear, low cost, cleanliness, high reliability, flexibility, and effective compliance for human use. As mentioned previously, it is suitable for use in rehabilitation engineering, medical nursing, and user-friendly therapeutic robots. In a recent report, PAMs were widely applied to the state-of-art rehabilitation machine. Xie and Jamwal [3] developed an iterative fuzzy controller to obtain excellent tracking performance for various trajectories with a rehabilitation robot driven by pneumatic muscle actuators. Anh [4] proposed a gain scheduling MIMO neural PID controller to obtain favorable angle tracking performance compared with a conventional PID controller for a 2-axes PAM robot under various loads. Lilly and Yang [5] applied a sliding mode controller to a planar arm actuated by two PMA groups; simulation results were consistent with theoretical findings for two different masses. Ahn and Anh [6] also developed an inverse double nonlinear autoregressive model with exogenous control based on the Takagi- Sugeno model applied in a PAM robot. A novel control structure based on a Takagi-Sugeno model [7] was proposed to track the desired trajectories, and simulation results illustrated the efficiency of the proposed approach for the new rehabilitation device.

The soft rehabilitation machine actuated by PAMs is highly nonlinear in behavior, model uncertainty and external disturbance. It is difficult to estimate an accurate dynamic model for model-based controller design. Hence, an adaptive self-tuning fuzzy controller which integrated adaptive fuzzy sliding mode control and functional approximation can be designed to solve these problems. Since the robustness is the best advantage of a sliding-mode control, it has been widely used to control model uncertainty and external disturbance. However, the traditional sliding-mode control has the model-based requirement for controller design. Though the fuzzy controller has been widely used in engineering applications, the fuzzy controller needs a time-consuming trial- and-error process and lacks the analysis for the stability and robustness problem. Thus, some researchers [8] - [10] developed the fuzzy sliding-mode control that combines the advantages of the sliding-mode control and fuzzy logic control.

Hence, the FA technique was adopted to release the model-based requirements and was used to design a sliding-mode controller for different nonlinear systems containing model uncertainties. In addition, the FA technique is used to expand and capture the system dynamic model and uncertainties by using finite linear combinations of basic functions with unknown constant weighting vectors. The update laws for weighting vectors of the functional approximation can be derived and the stability of the proposed controller is proven using the Lyapunov stability theorem. The experimental results verified that the proposed approach can be applied in the PAM system.

The remainder of this paper is organized as follows. In Section 2, the dynamic model is derived. In Section 3, the adaptive self-tuning fuzzy controller is presented. In Section 4, the experimental setup is described. Experimental results for output tracking are shown in Section 5. Finally, conclusions are drawn in Section 6.

2. System Dynamic Mode

Consider the single joint manipulator shown in Figure 1, which is indicative of the forces exerted by two PAMs. The variables and are control signals for generating and of each proportional valve. The relation between the control signal fed into any pressure proportional valve and the resultant pressure p is linear according to the static characteristics of the pressure proportional valve. The rotating torque is generated by the difference in pressure between the two opposing PAMs. That is, when as in Figure 1, the torque exerted on the joint is coun-

ter clock wise and the rotation of the joint is also counterclockwise. Therefore, the desired input pressure and for each PAM is generated using the following equation:

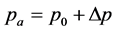(1)

where 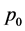is a nominal constant PAM pressure input, and 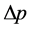is the control pressure input with an arbitrary function of time. Subscripts a and b denote the amount of inflation and deflation on the respective side. Hence, the dynamics of the system in Figure 1 can be described as

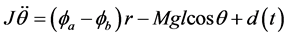(2)

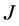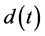where is the moment of inertia of the mass, is the total torque, is the external disturbance torque and 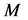is the mass. The total forces exerted by PAMs on the mass [11] are

(3)

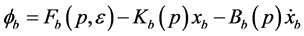(4)

where 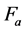and 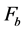can be expressed [12] as:

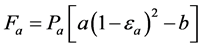(5)

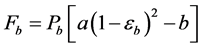(6)

Substituting (3) and (4) into (2) yields

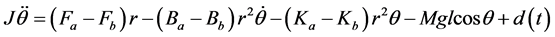(7)

where, ,

.

where is the initial muscle length.

Subsequently,

(8)

(9)

Substituting (8) and (9) into (7) obtains

(10)

Let, ,

and

Equation (10) can be rewritten as:

(11)

Equation (11) can be simplified as the following second-order model:

(12)

where x is the state vector, is a control gain, is a control signal, and is a an unknown time-varying function with an unknown variation bound. However, the bound of the unknown function can be estimated, in other word, , where and are known bound. The is defined as follows:

(13)

where is the nominal value and is a bounded uncertainty value.

(14)

Establishing an accurate dynamic model for model-based controller design is difficult because the system dynamics have nonlinear time-varying behavior with unknown uncertainty bounds. In this study, the functional approximation technique was employed to approximate this unknown function for releasing the model requirement.

3. Control Strategies

3.1. Fuzzy Sliding Mode Controller

The fuzzy sliding-mode controller (FSMC), shown functionally in Figure 2, is associated with a fuzzy logic control (FLC) structure, and a fuzzy slide surface to reduce the fuzzy rule number.

In many fuzzy logic control systems, the fuzzy rule table depends on error and error rate that complicate the fuzzy inference rules and the membership functions. In this study, a fuzzy sliding surface was introduced as a replacement, reducing the number of fuzzy sets and fuzzy inference rules. The fuzzy sliding surface

that combined error e and error rate on the phase plane could then be defined as

(15)

where is a positive constant. Therefore, the sliding surface variable s gradually converge to zero, and the sliding surface reaching condition is based on the Lyapunov theorem.

The sliding surface can be divided into 13 sections according to the membership function sets of . The membership function set for the control signal u is defined as. Therefore, the 13 × 13 fuzzy rule table with error e and error rate in the fuzzy logic control can be simplified as the 1 × 13 fuzzy rule table by using a fuzzy sliding surface as shown, in Figure 3.

The membership functions of fuzzy input and output variables, and the fuzzy rules of FSMC are shown in Figure 3. Hence, the control signal is derived from the fuzzy inference decision and defuzzification operation

(16)

where m is the number of rules and is the weight of the corresponding rule which has been activated. is the weight of each singleton fuzzy rules for constituting the control input u. is the consequent parameter which can be set to zero initially and then adjusted by an adaptive rule. The adaptive rule is derived from the Lyapunov stability analysis. This adaptive rule can eliminate the trial-and-error process for finding appropriate fuzzy rules in fuzzy control implementation.

3.2. Functional Approximation Technique

If a piecewise continuous time-varying function satisfies the Dirchlet condition, it can be transformed into a generalized Fourier series expansion within a time interval:

(17)

where, , and are the Fourier coefficients and is the frequency of the sinusoidal function. Define

(18)

(19)

Subsequently, (17) can be rewritten as

(20)

In finite term, (20) can be expressed as follows:

(21)

where is the approximation error. When n is large enough, can be approximated as follows:

(22)

Hence, the unknown time-varying function in (12) can be approximated by a linear combination of finite orthogonal basis functions to arbitrarily prescribed accuracy as long as n is large enough:

(23)

where is an orthogonal basis function vector and a weighting coefficient vector. If the number of the basis functions is large enough, (23) can be described as the following approximation form:

(24)

where is a orthogonal basis function vector and is a weighting coefficient vector. This FA (24) can be used to represent an unknown function with uncertainty. The time-varying is a known function the is an unknown regulating constant. A proper Lyapunov function can be selected to determine the update laws for these unknown constant based on Lyapunov stability theory.

3.3. Adaptive Self-Tuning Fuzzy Controller

The system control block diagram of the soft rehabilitation machineactuated by PAMs is shown in Figure 4. The sliding surface of this second-order system can be defined as

(25)

where the positive parameter s implies the convergent rate of on the sliding surface. The time derivative of s can be derived as

(26)

Substituting (12) into (26) yields

(27)

In order to achieve the sliding surface reaching condition and establish the approximation error compensation, the control law can be designed as:

(28)

where is the FA value of. The positive constant is a design parameter for achieving an appropriate robustness.

(29)

where and are assumed to be unknown bounded piecewise continuous functions and satisfy the Dirichlet conditions. Then, they can be expressed by the FA technique as follows

(30)

(31)

where are weighting vectors and is a vector of a basis Fourier series function. Hence, (29) can be rewritten as

(32)

where

(33)

To prove the stability of the control system and determine the update laws for vectors and, a Lyapunov function candidate is chosen as

(34)

where is a symmetric positive definite matrix. By taking the time derivative of the Lyapunov function candidate, the following can be obtained:

(35)

Because, (35) can be rewritten as

(36)

The update laws for and are chosen as

(37)

(38)

Therefore, (36) can be further rewritten as

(40)

To cover the uncertainty of the unknown function and establish an appropriate robustness, the parameter can be specified as

(41)

where and are the maximum values of and u, respectively. Subsequently, (39) results in

(42)

The control system stability can be guaranteed using the update laws (37) and (38). Equation (37) is the update law of the functional approximation coefficients. Equation (38) is the adjusting rule of the AFSMC fuzzy parameters. Based on Barbarlet’s lemma [13] the convergence of the system output error can be guaranteed using the control law u(t), (28).

4. Experimental Setup

The single joint rehabilitation machine actuated by PAMs is shown in Figure 5 which is used to simulate the arm’s motion. The experimental layout is shown in Figure 6 and the specifications are listed in Table 1. The maximum deformation of a PAM is 20% of its nominal length. Thus, the rotary range of angle extends from −40˚ to 40˚. The hardware includes an IBM-compatible personal computer, which calculates the control signal and controls a pressure proportional valve through a D/A card. Joint angles are detected by rotary potentiometers, the air pressure of each PAM is measured by pressure transducers, and the measurements are then fed back to the computer through an A/D card.

5. Experimental Studies

Reciprocated motion of rehabilitation machine can help patients for recovering extremity function. Therefore, to investigate output tracking performance, the proposed controller and fuzzy sliding-mode conroller associated with fixed fuzzy rules and scaling factors were implemented on an Intel Pentium 1.8 GHz PC, with a sampling time of 1 ms. The control software was coded in C++ programming language. The fixed fuzzy rules of the FSMC are presented in Figure 3. The parameters, , were chosen, because these were the optimal values obtained by trial-and-error.

Following control parameters are chosen for the ASTFC. The sliding surface parameter is chosen as 400. The robustness parameter can be estimated based on (40). It is selected as 100.The nominal value of the control gain was selected as 18000, whereas the weighting coefficients of the approximation series were updated at each sample step. In addition, it was found that the variation of the control gain is less than 20% of its nominal value. In other words, the following inequalities hold: and. In order to improve the control law chattering behaviour, the function in (28) is replaced by the saturation function sat with a boundary layer thickness. The weighting matrix of the Fourier series function coefficients is set as a small constant matrix to increase the converging speed. The first 12 terms of the Fourier series functions are chosen as the FA basis functions.

5.1. Sinusoidal Wave Response

Figure 7 shows the output sinusoidal wave response obtained using the ASTFC and the FSMC. As shown in Figure 7, the actual joint angle trajectory is close to the reference trajectory. The peak-peak error is defined as:

(42)

where is the input wave peak value, and is the output wave peak value. The maximum peak-peak error and phase lag are listed in Table 2. The tracking errors are shown in Figure 8, indicating that the tracking errors of both controllers are considerably close without external disturbance or loading.

5.2. Sinusoidal Wave Response under External Disturbance Torque

To investigate the robustness and adaptation of the ASTFC, an external disturbance signal as shown in Figure 9 are applied in the joint. The output tracking response obtained using the ASTFC and the FSMC is shown in Figure 10. The peak-peak error and phase lag are listed in Table 3. The tracking errors are shown in Figure 11. The peak-peak errors of the ASTFC are still maintained within 1.1%. The results indicate that the ASTFC can overcome external disturbance to achieve excellent tracking performance.

6. Conclusion

Designing a model-based controller for a soft rehabilitation machine actuated by PAMs is highly difficult be-

cause the system has parameter uncertainties, highly nonlinear properties, and time-varying behavior. An ASTFC was developed and successfully used to control the system. The stability of the ASTFC is guaranteed by means of the Lyapunov theorem. The experimental results show that the ASTFC can be applied effectively to achieve excellent tracking performance despite external disturbance.

Cite this paper

Ming‐Kun Chang, (2015) Adaptive Self‐Tuning Fuzzy Controller for a Soft Rehabilitation Machine Actuated by Pneumatic Artificial Muscles. Open Journal of Applied Sciences,05,199-211. doi: 10.4236/ojapps.2015.55020

References