Open Journal of Applied Sciences
Vol.05 No.02(2015), Article ID:53987,11 pages
10.4236/ojapps.2015.52006
Development of a Methodology to Evaluate Projects Using Dynamic Traffic Assignment Models
Pankaj Maheshwari, Alexander Paz
Transportation Research Center, University of Nevada, Las Vegas, USA
Email: maheshwa@unlv.nevada.edu, apaz@unlv.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 January 2015; accepted 9 February 2015; published 12 February 2015
ABSTRACT
The identification and selection of performance measures play an important role in any decision making process. Additionally, millions of dollars are spent on appropriate planning and identification of prospective projects for improvements. As a result, current practitioners spend a lot of time and money in prioritizing their limited resources. This research proposes two tasks: 1) estimation of performance measures using a simulation based on dynamic traffic assignment model, and 2) development of a methodology to evaluate multiple projects based on benefit-cost analysis. The model, DynusT, is used for the Las Vegas roadway network during the morning peak time period. A comparative analysis of the results from proposed methodology with existing California Benefit-Cost (Cal-B/C) models is presented. The results indicate that the new methodology provides an accurate benefit-cost ratio of the projects. In addition, it signifies that the existing Cal-B/C models underestimate the benefits associated with the prospective project improvements. The major contribution of this research is the simultaneous estimation of the performance measures and development of a methodology to evaluate multiple projects. This is helpful to decision makers to rank and prioritize future projects in a cost-effective manner. Planning and operational policies for the transportation systems can be developed based on the gained insights from this study.
Keywords:
Performance Measures, Travel Demand Models, Dynamic Traffic Assignment, Benefit-Cost Analysis, California Benefit-Cost Models

1. Introduction
The identification and selection of performance measures play an important role in any decision making pro- cess. This helps the policy makers to allocate appropriate resources for prospective future improvements and evaluate projects. A myriad of literature is available that captures multiple performance measures within the Transportation, Activity and Environmental systems [1] -[4] . These systems are interdependent and changes in one system directly affect the other. For example, continuous increase in vehicular traffic as a result of economic development results in increased fuel consumption, and that ultimately leads to increased CO2 emissions and air pollutants. These emissions have a huge impact on the human health, environment and the society, and are difficult to estimate in monetary terms. Some of the performance measures that can be estimated include crashes, emissions (greenhouse gases and air pollutants), fuel consumption, vehicle operating costs, travel time reliability, etc. The following literature presents state of the art models, techniques and applications used by researchers to estimate performance measures for transportation zones/corridors/networks and applied in different scenarios and alternatives.
There are primarily two type of models to assess effects on traffic safety; accident-risk-based models (ARBM), and accident prediction models (APM). ARBMs are descriptive models based on traffic accident and exposure data whereas APMs are based on available data to quantify the relationship between accidents and traffic characteristics (speed or flow). The ARBM assumes that the individual probability of being involved in a crash increases linearly with exposure. Lord [5] described the non-linear relationship between crashes and exposure. As a result, safety research primarily focused on APM [6] [7] . Basic APM used power function of the flow with geometric parameters for links [8] as well as intersections [9] . In addition, some models are based on traffic characteristics such as hourly volumes, speeds, densities and volume-capacity (v/c) ratios [10] .
Researchers have used simulation models or Travel Demand Models (TDM) to estimate emissions and fuel consumption. There are basically two types of emission models―average-speed based and instantaneous-speed based. Ahn and Rakha [11] illustrated the development of microscopic energy and emission models for eight light duty vehicles using nonlinear multiple regression and neural network techniques. The study indicated that fuel consumption and emissions are more sensitive to the level of vehicle acceleration as compared to the vehicle speed. Rakha et al. [12] and Ahn and Rakha [13] used instantaneous speed and acceleration based emissions model VT-micro and combined with Dynamic Traffic Assignment (DTA) model INTEGRATION to estimate emissions. Coelho et al. [14] formulated three instantaneous speed based functions to estimate emissions and integrated them with a SIDTA traffic model for roundabout analysis. Mensink and Cosemans [15] used the output from microscopic model PARAMICS to estimate emissions based on speed and acceleration. Paz et al. [16] analyzed a DTA model DynusT and the average-speed based emission model EMFAC to estimate emissions and fuel consumption for truck alternatives in the Las Vegas region. Their study was robust and was based on average hourly volume on any link in the network. However, using average hourly volumes may lead to slightly misleading calculations. Bai et al. [17] used the mesoscopic DTA model Dynasmart-P and EMFAC to estimate emissions for trip based as well as link based traffic data. Lin et al. [18] integrated DTA models with MOVES for project level emissions analysis.
Considering the level of resolution used to model network traffic flows, modeling approaches can be categorized as macroscopic, microscopic, or mesoscopic. Normally, macroscopic approaches involve static traffic assignment models that enable the estimation of flow patterns on a regional scale but without any temporal resolution. These types of models use macroscopic traffic flow relationships to determine link travel times based on link flows. The TDM aggregates the origin-destination (OD) matrices across all modes before the traffic assignment step. As a result, the model cannot differentiate between truck and car assignments. Hence, the TDM cannot be directly used to conduct the desired analysis. In addition, the implementation of a multiclass assignment using a TDM framework requires addressing algorithmic and computational issues. The primary difference between single class and multiclass models is that the travel cost functions for the latter are non-symmetric and non-separable, hence convex optimization techniques are not applicable [19] . In addition, TDM models cannot capture key dynamic characteristics such as congestion propagation (e.g., spillback/spillover).
In contrast, microscopic models enable the explicit modeling of individual vehicles as well as temporal variations in traffic flow in the order of 0.1 to 1.0 seconds. In addition, they illustrate detailed traffic characteristics, such as lane changing behavior, acceleration/deceleration, and queuing related phenomena like spillback/spil- lover. However, this type of modeling requires a substantial amount of computational time and data collection efforts. As a result, it is very difficult and expensive to develop them for large-scale systems.
To overcome some of these limitations, many emerging planning strategies such as congestion pricing and the operational deployment of information provision services require modeling approaches that enable a greater level of detail than macroscopic models and with a much larger geographical scope than microscopic models. Mesoscopic models combine micro and macro level capabilities and incorporate many time-dependent traffic flow characteristics, such as spillback/spillover on a regional-level scale. The DTA models load individual vehicles into the network and solve a traffic assignment problem considering the operational characteristics of vehicles. Hence, this study requires a DTA capability that considers multiples classes of vehicles in terms of their routing strategies and behavior including trucks and regular passenger cars.
There are differences in calculating performance measures using static vs dynamic approaches. Kockelman et al. [20] developed a framework in her “Project Evaluation Toolkit” for estimating many performance metrics, but using a static modeling approach. Iida [21] reviewed the basic concepts for road network reliability analysis and highlights the drawbacks of static traffic assignment. Jha et al. [22] highlighted emergency evacuation planning with microscopic traffic simulation and clearly suggested that static models are not appropriate for evacuation scenarios. Paz et al. [16] used DTA model, DynusT, to compute multiple performance measures and performed a benefit-cost analysis for truck alternatives in Las Vegas region. The aforementioned literature suggests that the DTA model provides the capability to estimate traffic characteristics in an accurate manner as compared to static approaches. As a result, this research proposes a DTA simulation model to estimate the relevant performance measures (travel time, crashes, emissions, fuel consumption and vehicle operating costs) for Las Vegas roadway network. The objective of this research is to simultaneously estimate multiple performance measures and provide a methodology to prioritize and rank projects. A benefit-cost analysis methodology is developed to evaluate the prospective projects and the results are compared with other methodologies such as California Benefit-Cost (Cal-B/C) models.
The paper is organized as follows. The simulation-assignment model, DynusT, and the estimation of performance measures are discussed in Section 2. Experiments are conducted in Section 3 to calculate the benefit-cost ratios for certain projects. Results and analysis are discussed in Section 4. Conclusions and recommendations are presented in Section 5.
2. Methodology
This section describes the modeling and analysis approach. A simulation-based dynamic traffic assignment technique is used to estimate traffic flow related characteristics. Different models are used to estimate multiple performance measures based on the traffic flow characteristics. Section 2.1 discusses the network modeling approach and Section 2.2 discusses the procedure to estimate performance measures.
2.1. Network Modeling
The simulation based DTA model used in this research is DynusT [23] . The input required by DynusT includes: network characteristics, origin and destination locations, signal control settings, and the time-dependent OD demand. The network characteristics include the number of lanes, link length, saturation flow rates, and speed limits; and were extracted from the existing TDM. The existing TDM for the Las Vegas Roadway Network was provided by the Regional Transportation Commission of Southern Nevada. The TDM also provided present demand for year 2012 and projected demand for years 2013, 2020, and 2030, based on the current and estimated socio-economic characteristics in the region. The actual signal settings were provided by the Freeway and Arterial System of Transportation of Las Vegas, Nevada. The signal settings for new signals and future conditions were estimated. This estimation typically is expensive and time consuming; therefore, to simplify the process as well as represent likely future conditions, all intersections were modeled as actuated control. A total of 791 signalized intersections were modeled for the Las Vegas roadway network.
Two separate OD demand matrices were imported from the TDM, one for passenger cars and one for trucks. The Las Vegas roadway network includes a total of 1646 Traffic Analysis Zones. The morning peak-period (6 AM to 9 AM) was modeled using the corresponding three-hour demand that was distributed for every 15-minute time interval. Hence, a total of twelve demand matrices were used to dynamically load the vehicles into the network. Considering the demand profile, it was determined that aggregation of demand was feasible and convenient for computational performance. After aggregation, the number of zones was reduced from 1646 to 696 and the entire model was consistently updated to reflect zoning changes. Based on the input files, the DTA model was used to determine the average network traffic flow pattern for a morning peak-period of a weekday. To measure the difference between the model results and the real-world, calibration was performed and simulated link counts were compared to actual link counts. Several iterations of calibration were conducted until at least 85% of the link counts were within 15% error region, as specified by the Federal Highway Administration Traffic Analysis Volume Toolbox III [24] .
2.2. Estimation of Performance Measures
This section provides a methodology to estimate the performance measures based on the output from DTA model. In addition, the monetary value (in dollars) associated with corresponding performance measure is also discussed. The inclusion of dollar value will help the decision makers in evaluating the projects for safety improvements. Also, this will benefit in allocating appropriate resources for overall system performance. The estimated performance measures include: Travel Time, Crashes, Emissions, Fuel Consumption and Vehicle Operating Costs.
2.2.1. Travel Time
Travel time for a network link is obtained directly from the DTA model. The peak hour volume is extracted based on hourly volumes. As a result, appropriate daily and yearly factors are used to convert it into annual travel time. A wage rate of $20/hour is recommended to compute the corresponding monetary costs associated with travel time.
2.2.2. Crashes
Safety estimations are computed using the ITS Deployment Analysis Systems methodology, developed by the Intelligent Transportation Systems (ITS) Joint Program Office of the US Department of Transportation [25] . This methodology relates volume-capacity ratios to average crash rates. Crash rates for the year 2012 were obtained from Nevada Traffic Crashes Report [26] . The IDAS default crash rates are multiplied by factor to reflect the characteristics of the Las Vegas roadway network. Hourly volume is obtained from the DTA model. Capacity is the product of the saturation flow rate and the number of lanes. Volume to capacity (v/c) ratios is computed to determine the appropriate crash rates. The number of crashes is estimated for three types: fatal, injury, and property damage only (PDO). The estimated number of crashes (in million VMT) in a network link for a specific crash type is given by Equation (1).
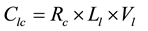 (1)
(1)
where,
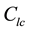 : Crashes for link l for crash type c;
: Crashes for link l for crash type c;
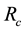 : Crash rate for crash type c (fatal, injury and PDO) in million VMT;
: Crash rate for crash type c (fatal, injury and PDO) in million VMT;
 : Link length for link l;
: Link length for link l;
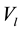 : Number of vehicles on link l (hourly).
: Number of vehicles on link l (hourly).
The total number of crashes is equal to the summation over the entire network of the number of crashes in each link. Comparison between estimated and actual crashes [27] suggested that actual fatal crashes were almost 87 percent higher and injury and PDO crashes were 50 - 60 percent higher than the estimated values. Hence, calibration factors were used to adequately estimate future crashes. To estimate the corresponding monetary cost, the number of crashes in each type is multiplied by cost factors [28] as shown in Equation (2).
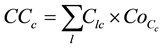 (2)
(2)
where,
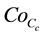 : Cost factor of crashes for crash type c;
: Cost factor of crashes for crash type c;
 : Cost of crashes for crash type c over the network.
: Cost of crashes for crash type c over the network.
2.2.3. Emissions
Emissions play a very important role in the evaluation of transportation alternatives because they are directly related to human health and the environment. Major pollutants from vehicles include carbon monoxide, volatile organic compounds, oxides of nitrogen, oxides of sulfur, carbon dioxide and particulate matter (PM10). This study uses Emission Rates (ER) in gm/mile provided by the California Air Resource Board [29] and based on the EMFAC 2011 model. These rates are dependent on link speeds determined using the DTA model. The actual speed of any vehicle type is obtained by dividing the distance travelled with the time taken to cross that link. The estimated emissions for each link in the network are given by Equation (3).
 (3)
(3)
where,
 : Emission rate of vehicle type v for vehicle I during time interval k;
: Emission rate of vehicle type v for vehicle I during time interval k;
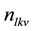 : Number of vehicles for vehicle type v on link l during time interval k;
: Number of vehicles for vehicle type v on link l during time interval k;
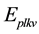 : Emission for pollutant p of vehicle type v on link l during time interval k (ton).
: Emission for pollutant p of vehicle type v on link l during time interval k (ton).
The emissions cost for each of the pollutants is obtained using Benefit/Cost models (Cal-B/C models) developed by the California Department of Transportation. It is assumed that the emissions cost in the Las Vegas Valley is the same as the cost in the Los Angeles/South Coast region. The monetary value of emissions (dollar/ton) in 2011 is based on the Cal-B/C models [28] . Thus, the emissions costs for each pollutant are given by Equation (4).
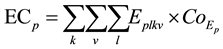 (4)
(4)
where,
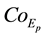 : Cost factor of emissions for pollutant type p;
: Cost factor of emissions for pollutant type p;
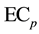 : Cost of emissions for pollutant type p over the network for entire simulation.
: Cost of emissions for pollutant type p over the network for entire simulation.
2.2.4. Fuel Consumption
Fuel consumption plays a vital role in the evaluation of investment of transportation projects. Fuel consumption rates (FC) (in gallons/mile), is obtained by EMFAC 2011 model. These rates are a function of link speeds that are obtained for each vehicle type using the simulation-based methodology. Fuel consumption for each link in the network is given by the Equation (5).
 (5)
(5)
where,



Based on the 2011 gas rates, gas cost for autos is assumed as $3/gallon and diesel cost for trucks is assumed as $3.4/gallon. Equation (6) shows the fuel consumption costs for any link in the network.

where,


2.2.5. Vehicle Operating Costs
Vehicle operating costs (VOC) depends on vehicle usage. Components that constitute VOC include fuel, oils, tires, maintenance, repairs, and mileage-dependent depreciation [30] . VOCs plays a vital role in the evaluation of investment of transportation projects because they include fuel and oils which is directly related to energy consumption and the environment. In this study, medium auto and truck costs were used to estimate VOC using Equation (7). Average VOC rates were obtained from Sinha and Labi [30] and are reported in cents/vehicle mile.

where,



The performance measures for years 2012, 2013, 2020, and 2030 is obtained from post processing the DynusT output and converted to monetary values as discussed in Section 2.2. It is assumed that the growth in between the years is linear and an inflation adjusted rate is used to calculate the respective benefits. Finally, all the benefits for future years are converted to present year using discount rate of 7% and added up to obtain total benefits. Similarly, the costs (right of way, construction, maintenance etc.) associated with a particular project is identified and converted to present value using the discount rate to obtain costs. As a result, the benefit-cost ratio is identified for the project. The entire analysis is coded and converted into an Interface. This interface is modular and the user defines the analysis year. The interface is flexible and it can estimate the performance measures based on link, corridor, zone, or a network depending on the specified time interval. For multiple alternatives, a zone is selected for each alternative and then the interface is run for that particular scenario to check the differences from the base case. The interface doesn’t have the capability to generate results for comparing multiple alternatives simultaneously.
Ideally, for transportation performance management, two types of economic analysis are performed. The first systematic means of comparing highway investments is called life-cycle cost analysis (LCCA) [31] . This me- thod applies the discount rate to the life cycle costs of alternatives and obtains the desired outcome based on the least cost. Additionally, LCCA is used where the benefits of the possible project alternatives are basically identical. The second means of evaluating the alternatives is benefit-cost analysis, which considers life-cycle benefits as well as life-cycle costs. Benefit-cost analysis reveals the alternative that maximizes the net benefits from allocation of available resources [31] . This research uses the benefit-cost analysis technique to evaluate the prospective projects.
3. Experimental Set-Up
This section discusses two techniques to obtain the benefit-cost ratio for projects in Las Vegas metropolitan area. The first one is the traditional Cal-B/C model [28] used predominately for the analysis of large scale networks as well as corridors. It is a PC-based spreadsheet model developed by the California’s economic analysis branch and consultants. It uses the TDMs that tend to be static and do not represent the dynamic nature of traffic that is available from simulation tools. Cal-B/C can be used to analyze many types of highway construction and operational improvement projects, as well as some Intelligent Transportation System (ITS) and transit projects. This tool has been widely used in the industry to evaluate multiple projects and alternatives. The second one is the proposed benefit-cost methodology developed using the performance measures derived from DTA models, such as DynusT. The performance measures are obtained bypost-processing the DynusT output and estimated for the Las Vegas roadway network. In addition, similar monetary values of time, emissions, crashes, fuel consumption, and vehicle operating costs are taken for both the techniques.
3.1. California Benefit-Cost Model
The California Department of Transportation uses Cal-B/C to conduct investment analyses of projects proposed for the State Transportation Improvement Program, the State Highway Operations and Protection Program, and other ad hoc analyses requiring benefit-cost analysis. Cal-B/C is a spreadsheet-based tool that can prepare analyses of highway, transit, and passenger rail projects. The model uses input data defining the type, scope, and cost of projects. The model calculates life-cycle costs, net present values, benefit-cost ratios, internal rates of return, payback periods, annual benefits, and life-cycle benefits [28] .
The benefit-cost analysis on three federally funded projects sponsored by the Nevada Department of Transportation (NDOT) was performed using Cal-B/C models. The analyses were formed from existing project reports and NDOT databases that contained project data. The benefit-cost analyses were performed using Cal-B/C with parameter and rate adjustments based on local conditions for Nevada. The following performance measures were considered in the evaluation of benefits and costs.
・ Travel Time Savings
・ Accident Reductions
・ Vehicle Operating Costs
・ Vehicle Emission Reductions
・ Pavement Roughness
・ Project Capital Costs
・ Project Operation & Maintenance Costs
These analyses all use a 20-year horizon to enable comparisons among each other. The analyses use a real discount rate of 7% as recommended by the Office of Management and Budget (OMB) Circular A-94 [32] .
3.2. Proposed Benefit-Cost Methodology
The proposed methodology uses the output obtained after running DynusT through the entire network. For analysis, a zone is selected near the proposed project. Figure 1(a) shows the selected zone with purple colored


Figure 1. (a) An example of zone selection within NEXTA; (b) An interface to estimate performance measures.
boundaries for one of the projects in Network EXplorer for Traffic Analysis (NEXTA). NEXTA is an interface used to facilitate the preparation, post-processing, and analysis of simulation-based dynamic traffic assignment datasets. The benefit-cost methodology uses an interface as shown in Figure 1(b). The interface calculates the performance measures based on techniques discussed in Section 2.2. The user inputs the start time/end time of the simulation, and the analysis year. Later, the button “Compute” is hit and the performance measures such as crashes, emissions, fuel consumption, vehicle operating costs, and travel time are displayed as shown in Figure 1(b). Finally, they are all converted to costs and ultimately combined to obtain the total costs for the selected zone.
Once improvements to the project are made, DynusT is run again to obtain a new set of output. The same zone is selected again and using the previous input data, the process is repeated to estimate the total costs. Finally, the net benefit of the project is the difference in total costs before and after the improvements. The net cost is the cost involved in project improvement/construction.
For any project, Figure 2(a) demonstrates the trend of performance measures with time on a 20-year time ho-


Figure 2. (a) Trend of travel time with time; (b) Percent distribution of costs based on individual performance measures.
rizon with a discount rate of 7%. The x axis represents the years whereas y axis represents total travel time in billions of hours. Figure 2(b) is obtained by clicking any column in Figure 2(a) and shows the percent distribution of the costs (in millions) based on individual performance measure.
4. Results and Analysis
The comparative analysis of the results of the benefit-cost ratio obtained from the proposed model and the Cal-B/C models is shown in Table 1. Project 1 is a new bridge construction project; Project 2 denotes a new bypass/interchange whereas Project 3 represents a pavement rehabilitation type of project. Ideally, from a decision maker’s perspective, projects are prioritized by their net present value of benefit-cost ratios. The higher the ratio, the more important is the project. For Cal-B/C model, the priorities are in following order: Project 1 > Project 3 > Project 2 whereas for proposed model, the priorities are as follows: Project 3 > Project 1 > Project 2. In addition, the analysis shows that the benefit-cost ratio for Project 1 has the minimum variance for the two techniques.
Figure 3(a) shows the benefit-cost analysis for the three projects based on the proposed methodology. The x axis indicates the type of project and the y axis represents the associated dollar amount in millions. The benefits associated with each project are compared with the base case and the difference is shown on positive y axis. The cost associated with the project is considered as negative and is shown on negative y axis. The benefit-cost ratio is obtained by dividing the total benefits with the total costs. Figure 3(b) shows the percent distribution of total benefits based on individual performance measures such as travel time, emissions, fuel consumption, crashes, and vehicle operating costs. As evident, travel time is a significant contributor of benefits for bridge and bypass projects. This is due to the capacity improvements resulting from construction of a new bridge or a bypass. For pavement project, the major contributors of benefits are travel time, fuel consumption and vehicle operating costs. This is clearly the result of resurfacing the pavement and its associated benefits. Smooth pavement helps in maintaining high speed resulting in improved travel time, better fuel efficiency and decrease in vehicle maintenance costs.
The results from Table 1 indicated that existing Cal-B/C models underestimate the benefits associated with the project. The proposed methodology provides an accurate benefit-cost ratio with respect to magnitude. The source of the differences is due to the differences in methodology (DTA vs TDM) as well as input data (volume and speed data). DTA typically constrains the v/c ratio to 1, while most TDMs have fewer constraints. The maximum v/c parameter in Cal-B/C models is 1.56 to obtain 5 MPH speed estimates for a free-flow speed of 70 mph [28] . In addition, the computation of travel time in both the models is a major factor in increased benefits for the proposed model as compared to Cal-B/C models. The proposed model uses the actual travel time for any vehicle based on the real travel speed whereas the Cal-B/C model uses average speed of the vehicles for analysis. The results also substantiate the use of DTA models for evaluating projects in a cost-effective manner.
5. Conclusions and Recommendations
Existing state of the art techniques concentrated primarily on estimation of performance measures using static approaches. However, to accurately estimate the traffic flow characteristics, dynamic models were predominately used by researchers. This research proposed a comprehensive methodology to estimate performance measures using DTA models and evaluate projects. The evaluation was done using the benefit-cost analysis techniques. Numerical experiments were conducted to evaluate three projects in Las Vegas Metropolitan area. A
Table 1. Summary of the results of benefit-cost analysis for multiple projects.


Figure 3. (a) Benefit-cost analysis for projects based on proposed methodology; (b) Percent distribution of benefits based on individual performance measures.
comparative analysis with the existing Cal-B/C models revealed that the proposed methodology provides an accurate benefit-cost ratio. In addition, the results also indicated that Cal-B/C models underestimate the benefits associated with the projects. The experiments showed that the proposed methodology is robust and it provides a suitable technique for decision makers to rank and prioritize projects. Planning and operational policies for the Transportation systems can be developed based on the gained insights from this study.
The major contribution of this research work is the simultaneous estimation of the performance measures and development of a methodology to evaluate multiple projects. However, there are certain limitations associated with this research. The comparative analyses presented here are for three projects, and certainly more projects could be added to provide deeper understanding of the differences among the benefit-cost ratio results. In addition, the interface presented in the proposed methodology can be improved further to generate results for comparing multiple alternatives simultaneously. Future work will attempt to address the above limitations.
References
- Jeon, C.M., Amekudzi, A.A. and Guensler, R.L. (2010) Evaluating Plan Alternatives for Transportation System Sustainability: Atlanta Metropolitan Region. International Journal of Sustainable Transportation, 4, 227-247. http://dx.doi.org/ 10.1080/15568310902940209
- Litman, T. (2007) Developing Indicators for Comprehensive and Sustainable Transport Planning. Transportation Research Record: Journal of the Transportation Research Board, 2017, 10-15. http://dx.doi.org/ 10.3141/2017-02
- Paz, A., Maheshwari, P., Kachroo, P. and Ahmad, S. (2013) Estimation of Performance Indices for the Planning of Sustainable Transportation Systems. Advances in Fuzzy Systems, 2013, Article ID: 601468. http://dx.doi.org/10.1155/2013/601468
- Maheshwari, P., Khaddar, R., Kachroo, P. and Paz, A. (2014) Dynamic Modeling of Performance Indices for the Planning of Sustainable Transportation Systems. Networks and Spatial Economics. http://dx.doi.org/10.1007/s11067-014-9238-6
- Lord, D. (2002) Issues Related to the Application of Accident Prediction Models for the Computation of Accident Risk on Transportation Networks. Transportation Research Record: Journal of the Transportation Research Board, 1784, 17-26.
- Lord, D. (2002) Application of Accident Prediction Models for Computation of Accident Risk on Transportation Networks. Transportation Research Record, 1784, 17-26. http://dx.doi.org/10.3141/1784-03
- Sawalha, Z. and Sayed, T. (2005) Transferability of Accident Prediction Models. Safety Science, 44, 209-219. http://dx.doi.org/10.1016/j.ssci.2005.09.001
- Greibe, P. (2003) Accident Prediction Models for Urban Roads. Accident Analysis & Prevention, 35, 273-285. http://dx.doi.org/10.1016/S0001-4575(02)00005-2
- Lord, D. and Persaud, B.N. (2004) Estimating the Safety Performance of Urban Road Transportation Networks. Accident Analysis and Prevention, 36, 609-620. http://dx/doi.org/10.1016/S0001-4575(03)00069-1
- Lord, D., Manar, A. and Vizioli, A. (2005) Modeling Crash-Flow-Density and Crash-Flow-V/C Ratio Relationships for Rural and Urban Freeway Segments. Accident Analysis and Prevention, 37, 185-199.
- Ahn, K. and Rakha, H. (2002) Estimating Vehicle Fuel Consumption and Emissions Based on Instantaneous Speed and Acceleration Levels. Journal of Transportation Engineering, 128, 182-190. http://dx.doi.org/10.1061/(ASCE)0733-947X(2002)128:2(182)
- Rakha, H., Ahn, K. and Trani, A. (2004) Development of VT-Micro Model for Estimating Hot Stabilized Light Duty Vehicle and Truck Emissions. Transportation Research Part D: Transport and Environment, 9, 49-74. http://dx.doi.org/10.1016/S1361-9209(03)00054-3
- Rakha, H. and Ahn, K. (2004) Integration Modeling Framework for Estimating Mobile Source Emissions. Journal of Transportation Engineering, 130, 183-193. http://dx.doi.org/10.1061/(ASCE)0733-947X(2004)130:2(183)
- Coelho, M.C., Farias, T.L. and Rouphial, N.M. (2006) Effect of Roundabout Operations on Pollutant Emissions. Transportation Research Part D: Transport and Environment, 11, 333-343. http://dx.doi.org/10.1016/j.trd.2006.06.005
- Mensink, C. and Cosemans, G. (2008) From Traffic Flow Simulations to Pollutant Concentrations in Street Canyons and Backyards. Environmental Modeling & Software, 23, 288-295. http://dx.doi.org/10.1016/j.envsoft.2007.06.005
- Paz, A., Veeramisti, N. and Maheshwari, P. (2011) Life-Cycle Benefit-Cost Analysis of Alternatives for Accommodating Heavy Truck Traffic in the Las Vegas Roadway Network. 13th TRB National Transportation Planning Applications Conference, Reno, May 8-12.
- Bai, S., Chiu, Y.C. and Niemeier, D.A. (2007) A Comparative Analysis of Using Trip-Based versus Link-Based Traffic Data for Regional Mobile Source Emissions Estimation. Atmospheric Environment, 41, 7512-7523. http://dx.doi.org/10.1016/j.atmosenv.2007.05.051
- Lin, J., Chiu, Y.C., Vallamsundar, S. and Bai, S. (2011) Integration of MOVES and Dynamic Traffic Assignment Models for Fine-Grained Transportation and Air Quality Analyses. Proceedings of the IEEE Integrated and Sustainable Transportation System, Vienna, June 29-July 1, 176-181.
- Patriksson, M. (2003) Algorithms for Computing Traffic Equilibria. Networks and Spatial Economics, 4, 23-38. http://dx.doi.org/10.1023/B:NETS.0000015654.56554.31
- Kockelman, K., Fagnant, D., Nichols, B. and Boyles, S. (2012) User’s Guide for PET: Project Evaluation Toolkit. A Sketch-Planning Toolkit for Evaluating Highway Transportation Projects. University of Texas at Austin, Austin.
- Iida, Y. (1999) Basic Concepts and Future Directions of Road Network Reliability Analysis. Journal of Advanced Transportation, 33, 125-134. http://dx.doi.org/10.1002/atr.5670330203
- Jha, M., Moore, K. and Pashaie, B. (2004) Emergency Evacuation Planning with Microscopic Traffic Simulation. Transportation Research Record, 1886, 40-48.
- Chiu, Y-C., Nava, E., Zheng, H. and Bustillos, B. (2010) DynusT User’s Manual.
- FHWA (2004) Traffic Analysis Toolbox Volume III: Guidelines for Applying Traffic Microsimulation Modeling Software. FHWA-HRT-04-040. US Department of Transportation, Washington DC.
- Cambridge Systematics Inc (2014) Intelligent Deployment Analysis Systems. Appendix B: IDAS Default Values. http://idas.camsys.com/documentation.htm
- NDOT (2010) Nevada Traffic Crash Report. Nevada Department of Transportation. http://www.nevadadot.com/uploadedFiles/NDOT/About_NDOT/NDOT_Divisions/Planning/Safety_Engineering/2010_Nevada_Traffic_Crashes.pdf
- NHTSA (2010) Fatality Analysis Reporting System. National Highway Traffic Safety Administration. http://www-fars.nhtsa.dot.gov/Main/index.aspx
- CALTRANS (2012) California Life-Cycle Benefit/Cost Analysis Model (Cal-B/C). California Department of Transportation. Cal-B/C Technical Supplement to User’s Guide, Vol. 3. http://www.dot.ca.gov/hq/tpp/offices/eab/LCBC_Analysis_Model.html
- CARB (2013) California Air Resources Board. EMFAC 2011. www.arb.ca.gov/msei/emfac2011-ldv-users-guide-final.pdf
- Sinha, K.C. and Labi, S. (2007) Transportation Decision Making: Principles of Project Evaluation and Programming. John Wiley and Sons, Inc., Hoboken. http://dx.doi.org/10.1002/9780470168073
- US Department of Transportation, Federal Highway Administration (2013) Economic Analysis Primer. http://www.fhwa.dot.gov/infrastructure/asstmgmt/primer05.cfm
- Office of Management and Budget (OMB) (1992) Circular A-94―Guidelines and Discount Rates for Benefit-Cost Analysis of Federal Programs.


