Open Journal of Applied Sciences
Vol.04 No.07(2014), Article ID:46863,24 pages
10.4236/ojapps.2014.47038
The Effect of Relative Humidity on Continental Average Aerosols
Bello Idrith Tijjani1, Aliyu Aliyu2, Fatima Sha’aibu3
1Department of Physics, Bayero University, Kano, Nigeria
2Department of Science Laboratory Technology, School of Technology, Kano State Polytechnic, Kano, Nigeria
3Girl’s Science and Technical College, Kano, Nigeria
Email: idrith@yahoo.com, idrithtijjani@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 April 2014; revised 28 May 2014; accepted 5 June 2014
ABSTRACT
In this paper, the authors extracted and investigated the effect of relative humidity (RH) on some microphysical and optical properties of continental polluted aerosols from OPAC (Optical Properties of Aerosols and Clouds) at the spectral range of 0.25 μm to 2.5 μm and eight relative humidities (0%, 50%, 70%, 80%, 90%, 95%, 98%, and 99%). The microphysical properties extracted were radii, volume, number and mass mix ratios as functions of RH while the optical properties were optical depth, extinction, scattering and absorption coefficients single scattering albedo, refractive indices and asymmetric parameters also at eight RHs. Using the microphysical properties, effective hygroscopic growth factors and effective radii of the mixtures were determined while using optical properties we determined the enhancement parameters, effective refractive indices and angstrom coefficients. Using the effective hygroscopic growth, we determined the dependence of the effective hygroscopicity parameter as a function of RH, while using enhancement parameters; we determined the effect of humidification factor on RH and wavelengths. The effective hygroscopic growth and enhancement parameters were then parameterized using some models to determine the effective hygroscopicity parameter, bulk hygroscopicity and humidification factors. We observed that the data fitted the models very well. The effective radii decrease with the increase in RH while the effective hygroscopic growth increases with the increase in RH, and this is in line with the increase in angstrom parameters, and this shows increase in mode size with the increase in RH. The angstrom coefficients show that the mixture has a bimodal type of distribution with the dominance of fine mode particles.
Keywords:
Microphysical Properties, Optical Properties, Hygroscopic Growth, Parametrization, Enhancement Parameters, Angstrom Coefficients, Effective Refractive Indices

1. Introduction
Aerosol particles in the atmosphere which comprised both soluble and insoluble aerosols, affect the earth’s radiation balance in both direct and indirect ways [1] . The direct effect is influenced by the hygroscopicity of the aerosol particles, while the indirect is the tendency for cloud formation and resulting cloud properties all due to changes in Relative humidity. The direct effect causes the scattering and absorption of short-wave solar and long-wave thermal radiation by the aerosol particulates. These changes in relative humidity modify the micro-physical (e.g., shape and size modification), chemical compositions (e.g. heterogeneous chemical reactions) and optical properties of not only the hygroscopic aerosol mixtures but also mixtures containing some contribution of non-hygroscopic aerosols like for example organic carbon or black carbon [2] [3] . Atmospheric aerosols undergo heterogeneous chemistry as they are transported through the atmosphere. These reactions cause Chemical Modification of the Atmosphere as well as Chemical Modification of the Airborne Mineral Dust Particles. These reactions have global implications. Changes in particle size and phase with relative humidity modify heterogeneous atmospheric chemistry, cloud and fog formation processes, and visibility [4] -[6] . Key factors in determining whether a particular aerosol has a net positive (heating) or negative (cooling) direct radiative forcing influence on the Earth’s radiation budget include the spatial distribution of the aerosol, its physical state and associated optical properties Haywood and Boucher [7] , which also depend on the hygroscopicity of the aerosol [8] . Hygroscopic properties of aerosol particles can be determined by their physical and chemical characteristics [9] [10] .
Atmospheric aerosols are normally either externally or internally mixtures of particles with different chemical compounds such as soots, sulphates, nitrates, organic carbons and mineral dusts [4] . The ratio between their fractions as well as their content of soluble material determines the hygroscopic growth of the overall aerosol. The state of mixing of these components is crucial for understanding the role of aerosol particles in the atmosphere. In recent years, much attention has been paid to the mixing state of soot in aerosols [11] -[16] , and this influences the optical properties and climate effects of aerosols.
On a global basis, sulfates, nitrates and chlorides that have the largest concentrations as inorganic aerosols saltscontribute the largest to the mass budget of fine atmospheric particles [17] -[19] . These aerosols are hygroscopic by nature, so as such most of their microphysical and subsequently their optical properties would be strongly influenced by the ambient relative humidity (RH). Based on recent studies, the effect of sulfate particles on the annual-average global direct radiative forcing, arising from the fluctuation of atmospheric particles between aqueous and solid state, is estimated up to as much as 24% [20] -[22] .
In hygroscopicity modelling, the Kohler Equation is often used to describe both the hygroscopic growth and the activation of aerosol particles to cloud droplets, based on the aerosol’s physicochemical properties [22] . Recently, several single-parameter schemes have been proposed to simplify the Kohler Equation. Hygroscopicity parameters such as κ and ρion have been defined as proxies of chemical composition to represent aerosol hygroscopic growth as well as the ability of aerosol particles to become cloud condensation nuclei (CCN) [24] [25] . From reviews of some observational data, Andreae and Rosenfeld [26] suggested that continental and marine aerosols on average tend to cluster into relatively narrow ranges of effective hygroscopicity (continental κ = 0.3 ± 0.1; marine κ = 0.7 ± 0.2). Some recent field studies also supported this view, although some show systematic deviations for certain regions and conditions. For example, Gunthe et al. [27] reported a characteristic value of κ = 0.15 for pristine tropical rainforest aerosols in central Amazonia, which are largely composed on secondary organic matter. Some researchers, for example Rissler et al. [5] and Tijjani et al., [28] overviewed several models which describe the aerosol hygroscopicity and the CCN activation, and discovered that the hygroscopicity parameter (κ) for the Kohler model is not always a constant with respect to RH, most especially for the range of RH above 90%.
The main parameter used to characterize the hygroscopicity of the aerosol particles based on some microphysical properties is the aerosol hygroscopic growth factor gf(RH), which is defined as the ratio of the particle diameter at any RH to the particle diameter at RH = 0% [4] [29] . The effects of hygroscopicity on the optical properties are described by the enhancement factors f(RH, l) of the optical parameters, which are defined as the ratio between values of the optical parameters at a given RH, and those in dry conditions (RH = 0).
The aim of this study is to determine the effects of RH and wavelength on the globally averaged direct aerosol radiative forcing, the effective hygroscopic growth and enhancement factors for continental average aerosols from the data extracted from OPAC. One and two variables parameterizations models will be perform to determine the relationship of the particles’ hygroscopic growth and enhancement parameters with the RH. Angstrom coefficients are used to determine the particles’ type and the changes in the mode size and type distributions as a result of the changes in RHs.
2. Methodology
The models extracted from OPAC are given in Table 1.
Where water soluble components, consist of scattering aerosols, that are hygroscopic in nature, such as sulfates and nitrates present in anthropogenic pollution, while water insoluble and soot are considered not soluble in water and therefore the particles are assumed not to grow with increasing relative humidity.
The globally averaged direct aerosol Radiative forcing, ∆FR, for absorbing aerosols was calculated using the Equation derived by Chylek and Wong [31]
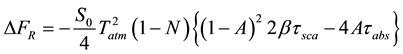 (1)
(1)
where S0 is a solar constant, Tatm is the transmittance of the atmosphere above the aerosol layer, N is the fraction of the sky covered by clouds, A is the albedo of underlying surface, β is the upscattering fraction of radiation scattered by aerosol into the atmosphere while τsca and τabs are the aerosol layer scattering and absorptions optical thickness respectively. The above expression gives the radiative forcing due to the change of reflectance of the earth-aerosol system. The upscattering fraction is calculated using an approximate relation [32]
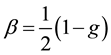 (2)
(2)
where g is the asymmetric parameter. The global averaged albedo A = 0.22 over land and A = 0.06 over the ocean with 80% of aerosols being over the land; solar constant of 1370 Wm−2, the atmospheric transmittance is taken to be Tatm = 0.79 [33] and cloudness N = 0.6.
The aerosol’s hygroscopic growth factor gf(RH), [4] [34] is defined as:
 (3)
(3)
where RH is taken for seven values 50%, 70%, 80%, 90%, 95%, 98% and 99%.
But since atmospheric aerosols consist of more and less hygroscopic sub fractions so the information on the hygroscopicity modes was merged into an “over-all” or “bulk” hygroscopic growth factor of the mixture, gfmix(RH), representative for the entire particle population as:
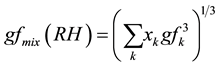 (4)
(4)
The effective or volume equivalent radius of the mixture was determined using the relation
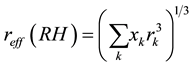 (5)
(5)
where the summation is performed over all compounds present in the particles and xk represent their respective volume fractions, using the Zdanovskii-Stokes-Robinson relation [35] -[38] . Solute-solute interactions are neglected
Table 1. Compositions of aerosols types at 0% RH [30] .
in this model and volume additivity is also assumed. The model assumes spherical particles, ideal mixing (i.e. no volume change upon mixing) and independent water uptake of the organic and inorganic components.
It can also be computed using the xk as the corresponding number fractions [39] -[45] and mass fractions [41] -[45] , but some discovered that volume fractions [41] -[46] .
The RH dependence of gfmix(RH) can be parameterized in a good approximation by a one-parameter equation, proposed e.g. by Petters and Kreidenweis [24] as:
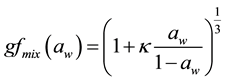 (6)
(6)
Here, aw is the water activity, which can be replaced by the relative humidity RH, if the Kelvin effect is negligible, as for particles with sizes more relevant for light scattering and absorption. The coefficient κ is a simple measure of the particle’s hygroscopicity and captures all solute properties (Raoult effect), that is, it is for the ensemble of the particle which can be defined in terms of the sum of its components. In an ensemble of aerosol particles, the hygroscopicity of each particle can be described by an “effective” hygroscopicity parameter κ [24] [47] . Here “effective” means that the parameter accounts not only for the reduction of water activity by the solute but also for surface tension effects [27] [48] [49] . It also scales the volume of water associated with a unit volume of dry particle [24] and depends on the molar volume and the activity coefficients of the dissolved compounds [50] . The κ value derived a particle of a given composition may vary, depending upon the size molar mass, the activity and RH it is derived at.
For atmospheric aerosols, the range of κ typically varies from as low as ∼0.01 for some combustion aerosol particles up to ∼1 for sea-salt particles [24] [26] [51] [52] .
The following sub-divisions at 85% RH were made by Swietlicki et al., [4] and Liu et al., [53] ; as: nearly-hydrophobic particles (NH): k <= 0.10 (gfmix <= 1.21), less-hygroscopic particles (LH): k = 0.10 − 0.20 (gfmix =1.21 − 1.37); more-hygroscopic particles (MH): k > 0.20 (gfmix > 1.37).
Making κ as the subject of the Equation (6), we get
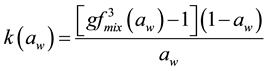 (7)
(7)
Humidograms of the ambient aerosols obtained in various atmospheric conditions showed that gfmix(RH) could as well be fitted well with a γ-law [54] -[58] as
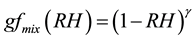 (8)
(8)
Making g as the subject of Equation (8) we get
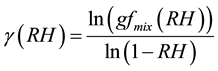 (9)
(9)
The bulk hygroscopicity factor B under subsaturation RH conditions was determined using the relation:
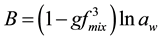 (10)
(10)
where aw is the water activity, which can be replaced by the RH as explained before.
The impact of hygroscopic growth on the optical properties of aerosols is usually described by the enhancement factor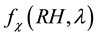 :
:
 (11)
(11)
where in our study RHref was 0%, and RH was taken for seven values of 50%, 70%, 80%, 90%, 95%, 98% and 99%.
In general, the relationship between 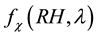 and RH is nonlinear [59] . In this paper, we determine the empirical relations between the enhancement parameter and RH [60] as:
and RH is nonlinear [59] . In this paper, we determine the empirical relations between the enhancement parameter and RH [60] as:
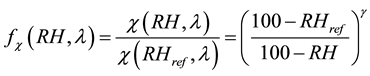 (12)
(12)
The g known as the humidification factor represents the dependence of aerosol optical properties on RH, which results from the changes in the particles sizes and refractive indices upon humidification. The use of g has the advantage of describing the hygroscopic behavior of aerosols in a linear manner over a broad range of RH values; it also implies that particles are deliquesced [61] , a reasonable assumption for this data set due to the high ambient relative humidity during the field study. The g parameter is dimensionless, and it increases with increasing particle water uptake.
Making g as the subject of Equation (12) and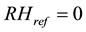 , we get
, we get

From previous studies, typical values of γ for ambient aerosol ranged between 0.1 and 1.5 [62] [63] .
Two parameters empirical relation was also used [59] [64] as;

Equations (12) and (14) are verified at wavelengths 0.25, 0.45, 0.55, 0.70, 1.25, and 2.50 µm.
To determine the effect of particles distributions as a result of change in RH, the angstrom exponent was determined using the spectral behavior of the aerosol optical depth, with the wavelength of light (λ) was expressed as inverse power law [65] :

The angstrom exponent was obtained as a coefficient of the following regression,

However Equation (16) was determined as non-linear (that is the angstrom exponent itself varies with wavelength), and a more precise empirical relationship between the optical depth and wavelength was obtained with a 2nd-order polynomial [41] -[45] [66] -[76] as:

and then we proposed the cubic relation to determine the type of mode distribution [41] -[45] as:

where β, α, α1, α2, α3 are constants that were determined using regression analysis with SPSS16.0. forwondows.
We also determined the exponential dependence of the aerosol optical thickness on relative humidity as done by Jeong et al. [59] as;

where A and B are constants determined using regression analysis with SPSS 16.0 and was computed at wavelengths 0.25, 1.25 and 2.50 mm.
We finally determine the effect of hygroscopic growth on the effective refractive indices of the mixed aerosols using the following formula [77] :

The relation between dielectrics and refractive indices is

We also used another mixing rule formula that has been used in the several widely employed databases of aerosol optical properties [30] [78] -[81] as:

where fi and εi are the volume fraction and dielectric constant of the ith component and ε0 is the dielectric constant of the host material. For the case of Lorentz-Lorentz [82] [83] , the host material is taken to be vacuum, ε0 = 1.
We then proposed the fi to be mass mix ratios and number mix ratios, to determine the advantage of one over the other.
The computations of Equations (20), (21) and (22) were done using the complex functions of Microsoft Excel 2010.
3. Results and Discussions
From Figure 1, it can be seen that the RF(warming) increases with the increase in wavelength but decreases with the increase in RH. The nature of the decrease in warming at shorter wavelengths signifies the dominance of fine mode particles.
From Table 2, it can be observe that there are increases in gfmix and reff, decreases in B and k while g fluctuates with the increase in RH.
The results of the parameterizations by one parameter of Equations (6) and (8) using number mix ratio are:
k = 0.0773, R2 = 0.9470 using Equation (6).
𝛾 = −0.1459, R2 = 0.9988 using Equation (8).
From the observations of R2, it can be seen that the data fitted the equations very well.
From Table 3, it can be observe that there are increases in gfmix and, decreases in, reff, B and k while g fluctuates with the increase in RH.
The results of the parameterizations by one parameter of Equations (6) and (8) using volume mix ratio are:
k = 0.1569, R2 = 0.9620 using Equation (6).
𝛾 = −0.1972, R2 = 0.9997 using Equation (8).
From the observations of R2, it can be seen that the data fitted the Equations very well.
From Table 4, it can be observe that there are increases in gfmix, decreases in, reff B and k while g fluctuates with the increase in RH.
Figure 1. A graph of radiative forcing against wavelengths.
Table 2. The table of hygroscopic growth factors, effective radii, B (bulk hygroscopicity), k (hygroscopicity) and g (Humidification factor), of the aerosols using number mix ratio.
Table 3. The table of hygroscopic growth factors, effective radii, B (bulk hygroscopicity), k (hygroscopicity) and g (Humidification factor), of the aerosols using volume mix ratio.
Table 4. The table of hygroscopic growth factors, effective radii, B (bulk hygroscopicity), k (hygroscopicity) and g (Humidification factor), of the aerosols using mass mix ratio.
The results of the parameterizations by one parameter of Equations (6) and (8) using mass mix ratios are:
k = 0.1487, R2 = 0.9674 using Equation (6).
𝛾 = −0.1910, R2 = 0.9991 using Equation (8).
From the observations of R2, it can be seen that the data fitted the Equations very well.
From Figure 2, it can be observed that all the gfmix have non-linear relation with RH as confirmed by our simulation using Equations (6) and (8). It can also be observe that from the figure that the plots for volume is the highest followed by mass and the number mix ratio has the least. These observations are also confirmed from our simulated results with the coefficient k being highest for volume and the least for number, and the exponent g being highest in magnitude in volume and values having least using number mix ratios.
From Figure 3, the plots of reff against RH show non-linear relation. It can also be observed that the plot for number mix ratio has the least reff but the problem with it is that it is increasing with RH, and this is contrary to the behavior of our radiative forcing which shows the dominance of fine mode particles. However, the plots for volume and mass decrease with the increase in RH and these reflect the behavior of the radiative forcing in Figure 1.
From Figure 4, it can be seen that all the plots have non-linear relation with RH. From the figure it can be observe that the plot for number has the least value but because of the size and hygroscopic nature of water soluble compared to that of soot, it can be concluded that number mix ratio cannot be useful. For the figure it can be seen that volume has the highest B followed by the mass and this shows that volume representation can be the best.
Figure 2. A graph of gfmix against RH using number, volume and mass mix ratios using the data from Tables 2-4.
Figure 3. A graph of effective radii against RH using number, volume and mass mix ratios using the data from Tables 2-4.
Figure 5 is almost similar to Figure 4, though the maximum of hygroscopicity is higher than that of Bulk. As stated in Figure 4, and also compare with the results of our simulations of Equation (6), it can be stated that volume mix ratio can be a better parameter for the analysis of the hygroscopic nature of the aerosols.
From Figure 6, it can be seen that all the plots have non-linear relation with the increase in RH. It can also be observe that g for number mix ratio has the least value in magnitude while it has the highest magnitude using volume mix ratio.
From Figure 7, it can be observe that the optical depth follows a relatively smooth decrease with wavelength for all RHs and can be approximated with power law wavelength dependence. It is evident from the figures that there is relatively strong wavelength dependence of optical depth at shorter wavelengths that gradually decreases towards longer wavelengths irrespective of the RH, attributing to the dominance of fine over coarse particles.
Figure 4. A graph of B (bulk hygroscopicity) against RH using number, volume and mass mix ratiosusing the data from Tables 2-4.
Figure 5. A graph of k (hygroscopicity) against RH using number, volume and mass mix ratios using the data from Tables 2-4.
The presence of a higher concentration of the fine-mode particles which are selective scatters enhance the irradiance scattering in shorter wavelength only while the coarse-mode particles provide similar contributions to the optical depth at both wavelengths [84] . It also shows that hygroscopic growth has more effect on fine particles than coarse particles.
The data that were used in plotting Figure 7 were applied to Equation (18), at the wavelengths of 0.25, 1.25 and 2.50 μm. The results obtained are as follows:
At λ = 0.25, A = 0.1408, B = 1.5013, R2 = 0.7070.
At λ = 1.25 μ, A = 0.0170, B = 1.7296, R2 = 0.6127.
At λ = 2.50 μ, A = 0.0063, B = 1.1916, R2 = 0.5085.
The relation between optical depth and RH shows decrease in R2 but the exponent B fluctuates with the
Figure 6. A graph of g against RH using number, volume and mass mix ratios using the data from Tables 2-4.
Figure 7. A graph of optical depth against wavelengths.
increase in wavelength. This signifies the dominance of fine mode particles that are more related at smaller wavelengths.
From Table 5, it can be observed that from the linear part a increases with the increase in RH, though at the delinquent points (95% to 99%) it decreases with the increase in RH, and this signifies the increase in the dominance of fine particles over coarse particles. The sign of a2 (which signifies the curvature) together with the increase as the RH increases reflects the increase in the dominance of small particles as a result of the sedimentation of coarse mode particles with the increase in RH. The cubic part signifies mode distributions as bi-modal with the dominance of fine mode particles.
Figure 8 show that the enhancement factors increase with the increase in RH and wavelengths in almost non- linear form. The most interesting phenomena is the visible range window (0.4 - 0.7 µm) and the near-infrared (0.7 - 1.0) where the enhancement is higher with the increase in RH. This shows that at this spectral range, most of the solar radiation passes through to the surface and enables solar radiation to “deliver” the bulk of its energy to the surface (for use in climate processes).
Table 5. The results of the angstrom coefficients for optical depth using Equations (16), (17) and (18) at the respective relative humidities using regression analysis with SPSS16 for windows.
Figure 8. A graph of enhancement parameter for optical depth against wavelengths.
The data that were used in plotting Figure 8 were applied for the parametrisations of Equations (12) and (14), at the wavelengths of 0.25, 0.45, 0.55, 0.70, 1.25 and 2.50 μm. The results obtained are as follows:
For a single parameter using Equation (12):
At λ = 0.25 μ, γ = 0.3817, R2 = 0.9994.
At λ = 0.45 μ, γ = 0.4199, R2 = 0.9988.
At λ = 0.55 μ, γ = 0.4315, R2 = 0.9983.
At λ = 0.70 μ, γ = 0.4429, R2 = 0.9976.
At λ = 1.25 μ, γ = 0.4287, R2 = 0.9914.
At λ = 2.50 μ, γ = 0.2897, R2 = 0.9592.
For two parameters using Equation (14):
At λ = 0.25 μ, a = 0.9369, b = −0.3740, R2 = 0.9980.
At λ = 0.45 μ, a = 1.0922, b = −0.4318, R2 = 0.9960.
At λ = 0.55 μ, a = 1.1449, b = −0.4506, R2 = 0.9954.
At λ = 0.70 μ, a = 1.2028, b = −0.4701, R2 = 0.9947.
At λ = 1.25 μ, a = 1.4716, b = −0.4878, R2 = 0.9891.
At λ = 2.50 μ, a = 2.1339, b = −0.3798, R2 = 0.9642.
For one parameter, the exponent g increases as the wavelength is increased from ultra violet to solar spectral window and has maximum value at 0.7 mm but at the near infrared it decreases with the increase in wavelengths.
For two parameters, the exponent b increases as the wavelength is increased from uv to near infrared region and attained maximum at 1.25 mm.
From Figure 9 it can be observe that g is dependent on the spectral interval. For example, at the spectral interval of near ultra-violet and visible region (0.25 to 0.70 m) g increases with the increase in wavelength as the RH increases. But at the near infrared (0.70 to 2.50 m) it decreases with wavelength but fluctuates with the increase in RH. This shows the dominance of fine mode particles that absorbed more water at the spectral interval of 0.25 to 0.70 mm, while coarse mode particles at the spectral interval of 0.7 to 2.50 their absorption of water decreases with the increase in wavelengths.
From Figure 10, it can be observe that the plots are similar to those of Figure 7. The only difference is that the plots for optical depths are higher than the plots of extinction coefficients.
The data that were used in plotting Figure 10 were applied to Equation (19), at the wavelengths of 0.25, 1.25 and 2.50 μm. The results obtained are as follows:
At λ = 0.25, A = 0.0614, B = 1.6963, R2 = 0.7347.
At λ = 1.25 μ, A = 0.0077, B = 1.9007, R2 = 0.6340.
At λ = 2.50 μ, A = 0.0032, B = 1.2592, R2 = 0.5151.
The relation between extinction coefficients and RH shows decrease in R2 but the exponent B fluctuates with the increase in wavelength. This signifies the dominance of fine mode particles that are more active at shorter wavelengths.
From Table 6, it can be observed that the behaviors of the coefficients with RH are almost similar to those of Table 5.
From the plots of Figure 11, it can be observe that they are similar to those of Figure 8. The main difference between the plots of the two figures is that the enhancements for the extinction coefficients are higher than those of optical depths.
The data that were used in plotting Figure 11 were applied for the parametrisations of Equations (12) and (14), at the wavelengths of 0.25, 0.45, 0.55, 0.70, 1.25 and 2.50 μm. The results obtained are as follows:
For a single parameter using Equation (12).

Figure 9. A graph of g against wavelength using Equation (13).

Figure 10. A graph of extinction coefficients against wavelengths.
Table 6. The results of the angstrom coefficients for extinction coefficient using Equations (16), (17) and (18) at the respective relative humidities using regression analysis with SPSS16 for windows.
At λ = 0.25 μ, γ = 0.4342, R2 = 0.9988.
At λ = 0.45 μ, γ = 0.4765, R2 = 0.9994.
At λ = 0.55 μ, γ = 0.4885, R2 = 0.9994.
At λ = 0.70 μ, γ = 0.5013, R2 = 0.9991.
At λ = 1.25 μ, γ = 0.4739, R2 = 0.9949.
At λ = 2.50 μ, γ = 0.3069, R2 = 0.9629.
For two parameters using Equation (14).
At λ = 0.25 μ, a = 0.8219, b = −0.4090, R2 = 0.9989.
At λ = 0.45 μ, a = 0.9556, b = −0.4698, R2 = 0.9977.
At λ = 0.55 μ, a = 0.9956, b = −0.4879, R2 = 0.9974.
At λ = 0.70 μ, a = 1.0606, b = −0.5108, R2 = 0.9966.
At λ = 1.25 μ, a = 1.3389, b = −0.5216, R2 = 0.9922.
At λ = 2.50 μ, a = 2.0788, b = −0.3982, R2 = 0.9671.
For one parameter, the exponent g increases as the wavelength is increased J from ultra violet to solar spectral

Figure 11. A graph of enhancement parameter for extinction coefficients against wavelengths.
window and has maximum value at 0.7 mm but at the near infrared it decreases with the increase in wavelengths. For two parameters, the exponent b increases as the wavelength is increased from uv to near infrared region and attained maximum at 1.25 mm.
From Figure 12, by comparing the plots in Figure 9, with those of Figure 12, it can be observe that they are similar. The main difference between them is that the g for the extinctions with RH are higher than those of optical depth.
From Figure 13, by comparing the nature of the plots in Figure 13, with those of Figure 7 and Figure 10, it can be observe that they are similar. The main difference between them and Figure 13 is that the plots in Figure 13 have lower values compared with the other two.
From Figure 14, it can be observe that the plots are similar to those in Figure 8 and Figure 11. The main difference between them is that, the plots in Figure 14 have higher values than the other two.
Figure 15 shows that absorption is barely dependent of hygroscopic growth at smaller wavelengths but increases very slightly as the wavelengths increase. This shows that the absorptions of coarse particles are more dependent in RH than the fine particles. The plots can be approximated by power law.
Figure 16 shows that the enhancement parameter increases with the increase in wavelengths and this implies increase with the increases of the particle size as observed in Figure 15. Enhancement factor as a function of RH shows a nonlinear relation.
From Figure 17 it can be observe that increase in RH cause smaller particles to scatter more in the forward but decreasesthe forward scattering for bigger particles.
From Figure 18, it can be seen that hygroscopic growth enhances more scattering than absorption, and that is why the single scattering albedo is increasing with the increase in RH. Its relation with wavelengths shows that at the near ultraviolet region it increases with the increase in wavelength but at visible to near infrared regions it decreases with the increase in wavelengths. This is in line with our observation in Figure 16 that larger particles absorb light more at larger wavelengths.
Figure 19 shows that effective refractive indices decrease with the increase in RH.
With respect to wavelengths, at 0% RH at the visible spectral wavelength, the plots are constant with the increase in wavelengths. This shows the dominance of fine spherical particles, but as the RH increases, the plots at this spectral range became dependent with wavelengths and this shows that hygroscopic growth can cause the spherical particle to become non-spherical. This shows that increase in RH causes the particles to be more non-spherical with wavelengths.

Figure 12. A graph of g for extinction against wavelengths.

Figure 13. A graph of scattering coefficients against wavelengths.
From Figure 20, the behavior of the effective imaginary refractive indices with wavelengths shows the dominance of non-spherical particles. It also shows decrease in refractive indices as a result of the increase in hygroscopic growth. As the RH increases the relation between the imaginary effective refractive indices and wavelength become more linear.
From Figure 21, by comparison, it can be observed that Figure 21 and Figure 19 are similar, but the values of the plots for Figure 19 are a bit higher than those of Figure 21.
From Figure 22, by comparison, it can be observed that Figure 20 and Figure 22 are similar, but the plots in Figure 22 are a bit higher than those of Figure 20.
4. Conclusions
Comparing the three types of gfmix obtained, it can be seen that using volume and mass mix ratios gave better

Figure 14. A graph of scattering enhancement against wavelengths.

Figure 15. A graph of absorption coefficients against wavelengths.
representations of the mixture. These also imply that optical effects of atmospheric aerosols are also more closely related to their volume than their number [85] [86] . The modeling shows that increase in RH causes decrease in the effective radii, and this is what caused the optical depth and extinction, and scattering coefficients to have higher values at smaller wavelengths with the increase in RH [3] . The relations of these optical properties with RH are such that at the deliquescence point (95% to 99%) this growth with higher humidities increases substantially, making this process strongly nonlinear with relative humidity [3] [87] [88] . This shows that hygroscopic growth in smaller particles reveals an immense potential of light scattering enhancement in the forward scattering [89] while in larger particles it causes increase in the backward scattering at high humidities and the potential for being highly effective cloud condensation nuclei. It also shows that the mixture is internally mixed for smaller particles because of the increase in forward scattering as a result of the hygroscopic growth [79] and the increase in absorption despite decrease in effective imaginary refractive indices.
Despite the excellent relation shown for k and g using Equations (6) and (8), but by observing their values

Figure 16. A graph of absorption enhancement against wavelengths.

Figure 17. A graph of Asymmetric parameter against wavelengths.
using Equations (7) and (9) in Tables 2-4, it can be observed that the values of these parameters in Equation (6) and (8) could seriously underestimate those of Equation (7) and (8) most especially at lower RHs. We discovered that the exponents of the Equations (7) and (9) can be dependent on RH as shown in Tables 2-4 and also as determined by Rissler et al. [5] , but because of the excellent relation between gfmix and RH using Equations (6) and (8), the coefficient and the exponent can be constant, because it shows that the overestimation and overestimation can be negligible. The modeling of gfmix with Equations (6) and (8) show excellent relation because of the values of R2, and all converge to 1 as the RH or aw approach 0. The values of R2 for Equation (6) is always less than that of Equation (8), and this may be attributed to the kelvin effect of Equation (6) which was neglected.
From the modeling of the enhancement parameters using Equations (12) and (14), it can be observe that there is a very excellent relation. However, based on convergence the convergence behavior of the two models as RH

Figure 18. A graph of single scattering albedo against wavelengths.

Figure 19. A plot of real effective refractive indices against wavelength using Equation (20).
approaches 0, it can be seen that Equation (12) is better, because at this limit it approaches 1, which is what it is supposed to be.
Jeong et al. [59] demonstrated an exponential dependence of the aerosol optical thickness on relative humidity. The behavior of exponential relation between optical depth and extinction coefficients with RH shows that it is sensitive to the change in the effective radii. This is because it shows that for smaller particles, the relation is better at shorter wavelengths.
The increase in the angstrom constant and curvature with RH is in line with the decrease in the effective radii with the increase in RH. As the RH increases the value of α also continue to increase until at 95% RH when it started decreasing and continued to decrease, which implies that as from 95% RH the particles are becoming quite large in size, because of swelling of water vapor and aging processes. As a consequence of such a non-uniform increase, the Ångström coefficient also becomes a function of RH. The observed variations in

Figure 20. A plot of imaginary effective refractive indices against wavelength using Equation (20).

Figure 21. A plot of real effective refractive indices against wavelength using Equation (22).
angstrom coefficients can be explained by changes in the effective radii of the mixture resulting from changes in RH: the larger the number of small aerosol particles, the smaller the effective radius and the larger the angstrom coefficient. A greater content of small aerosol particles causes the effective radius to decrease and the angstrom coefficient to increase. An increase in RH influences the size of hygroscopic particles and, consequently, the effective radius of an aerosol mixture. Therefore, it can be concluded that, increase in hygroscopic growth as a result in the increase in RH in continental average aerosols causes decrease in the effective radii and this caused increase in optical depth, scattering and extinction coefficients more at lower wavelengths and this finally caused increase in the mode size distributions in the form of increasing angstrom coefficients.
Finally, the data fitted our models very well and can be used to extrapolate the hygroscopic growth at any RH

Figure 22. A plot of imaginary effective refractive indices against wavelength using Equation (22).
and enhancement parameters at any RH and wavelengths. The importance of determining gfmix(RH) as a function of RH and volume fractions, mass fractions and number fractions, and enhancement parameters as a function of RH and wavelengths can be potentially important because it can be used for efficiently representing aerosols-water interactions in global models.
About the two formulas used for the computations of the effective refractive indices, it can be concluded that they are the same, because they gave almost similar plots at the same computational platform, that is, they display the same information.
References
- Solomon, S., Qin, D., Manning, M., Alley, R.B., Berntsen, T., Bindoff, N.L., Chen, Z., Chidthaisong, A., Gregory, J.M., Hegerl, G.C., Heimann, M., Hewitson, B., Hoskins, B.J., Joos, F., Jouzel, J., Kattsov, V., Lohmann, U., Matsuno, T., Molina, M., Nicholls, N., Overpeck, J., Raga, G., Ramaswamy, V., Ren, J., Rusticucci, M., Somerville, R., Stocker, T.F., Whetton, P., Wood, R.A. and Wratt, D. (2007) Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change―Technical Summary. Cambridge University Press, Cambridge, 19-92.
- McFiggans, G., Artaxo, P., Baltensperger, U., Coe, H., Facchini, M.C., Feingold, G., Fuzzi, S., Gysel, M., Laaksonen, A., Lohmann, U., Mentel, T.F., Murphy, D.M., O’Dowd, C.D., Snider, J.R. and Weingartner, E. (2006) The Effect of Physical and Chemical Aerosol Properties on Warm Cloud Droplet Activation. Atmospheric Chemistry and Physics, 6, 2593-2649. http://www.atmos-chem-phys.net/6/2593/2006/ http://dx.doi.org/10.5194/acp-6-2593-2006
- Kuśmierczyk-Michulec, J. (2009) Ångström Coefficient as an Indicator of the Atmospheric Aerosol Type for a Well- Mixed Atmospheric Boundary Layer: Part 1: Model Development. Oceanologia, 51, 5-38. http://dx.doi.org/10.5697/oc.51-1.005
- Swietlicki, E., Hansson, H.C., Hämeri, K., Svenningsson, B., Massling, A., McFiggans, G., McMurry, P.H., Petäjä, T., Tunved, P., Gysel, M., Topping, D., Weingartner, E., Baltensperger, U., Rissler, J., Wiedensohler, A. and Kulmala, M. (2008) Hygroscopic Properties of Submicrometer Atmospheric Aerosol Particles Measured with H-TDMA Instruments in Various Environments: A Review. Tellus B, 60, 432-469. http://dx.doi.org/10.3402/tellusb.v60i3.16936
- Rissler, J., Svenningsson, B., Fors, E.O., Bilde, M. and Swietlicki, E. (2010) An Evaluation and Comparison of Cloud Condensation Nucleus Activity Models: Predicting Particle Critical Saturation from Growth at Subsaturation. Journal of Geophysical Research: Atmospheres, 115, Published Online. http://dx.doi.org/10.1029/2010JD014391
- Cheng, Y.F., Wiedensohler, A., Eichler, H., Heintzenberg, J., Tesche, M., Ansmann, A., Wendisch, M., Su, H., Althausen, D., Herrmann, H., Gnauk, T., Brüggemann, E., Hu, M. and Zhang, Y.H. (2008) Relative Humidity Dependen- ce of Aerosol Optical Properties and Direct Radiative Forcing in the Surface Boundary Layer at Xinken in Pearl River Delta of China: An Observation Based Numerical Study. Atmospheric Environment, 42, 6373-6397. http://dx.doi.org/10.1016/j.atmosenv.2008.04.009
- Haywood, J.M. and Boucher, O. (2000) Estimates of the Direct and Indirect Radiative Forcing Due to Tropospheric Aerosols: A Review. Reviews of Geophysics, 38, 513-543. http://dx.doi.org/10.1029/1999RG000078
- Tang, I.N., Tridico, A.C. and Fung, K.H. (1997) Thermodynamic and Optical Properties of Sea Salt Aerosols. Journal of Geophysical Research: Atmospheres, 102, 23269-23275.
- Topping, D.O., McFiggans, G.B. and Coe, H. (2005) A Curved Multi-Component Aerosol Hygroscopicity Model Framework: Part 1-Inorganic Compounds. Atmospheric Chemistry and Physics, 5, 1205-1222. http://dx.doi.org/10.5194/acp-5-1205-2005
- Topping, D.O., McFiggans, G.B. and Coe, H. (2005) A Curved Multicomponent Aerosol Hygroscopicity Model Framework: Part 2-Including Organic Compounds. Atmospheric Chemistry and Physics, 5, 1223-1242. http://dx.doi.org/10.5194/acp-5-1223-2005
- Jacobson, M.Z. (2001) Strong Radiative Heating Due to the Mixing State of Black Carbon in Atmospheric Aerosols. Nature, 409, 695-697. http://dx.doi.org/10.1038/35055518
- Moffet, R.C. and Prather, K.A. (2009) In-Situ Measurements of the Mixing State and Optical Properties of Soot with Implications for Radiative Forcing Estimates. Proceedings of the National Academy of Sciences of the United States of America, 106, 11872-11877. http://dx.doi.org/10.1073/pnas.0900040106
- Riemer, N., West, M., Zaveri, R.A. and Easter, R.C. (2009) Simulating the Evolution of Soot Mixing State with a Particle-Resolved Aerosol Model. Journal of Geophysical Research: Atmospheres, 114, Published Online. http://dx.doi.org/10.1029/2008JD011073
- Riemer, N., West, M., Zaveri, R. and Easter, R. (2010) Estimating Black Carbon Aging Time-Scales with a Particle- Resolved Aerosol Model. Journal of Aerosol Science, 41, 143-158. http://dx.doi.org/10.1016/j.jaerosci.2009.08.009
- Zhang, R., Khalizov, A. F., Pagels, J., Zhang, D., Xue, H. and McMurry, P.H. (2008) Variability in Morphology, Hygroscopicity, and Optical Properties of Soot Aerosols during Atmospheric Processing. Proceedings of the National Academy of Sciences of the United States of America, 105, 10291-10296. http://dx.doi.org/10.1073/pnas.0804860105
- Oshima, N., Koike, M., Zhang, Y., Kondo, Y., Moteki, N., Takegawa, N. and Miyazaki, Y. (2009) Aging of Black Car- bon in Outflow from Anthropogenic Sources Using a Mixing State Resolved Model: Model Development and Evaluation. Journal of Geophysical Research: Atmospheres, 114, Published Online. http://dx.doi.org/10.1029/2008JD010680
- IPCC (2007) Climate Change 2007: The Scientific Basis. In: Solomon, S., Ding, Y., Griggs, D.G., Noguer, M., Vanderlinden, P.G., Dai, X., Maskell, K. and Johnson, C.A., Eds., Contribution of Working Group I to the 4th Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge.
- Li, W.F, Bai, Z.P., Liu, A.X., Chen, J. and Chen, L. (2009) Characteristics of Major PM2.5 Components during Winter in Tianjin, China. Aerosol and Air Quality Research, 9, 105-119. http://dx.doi.org/10.4209/2008.11.0054
- Shen, Z.X., Cao, J.J, Tong, Z., Liu, S.X., Reddy, L.S.S., Han, Y.M, Zhang, T. and Zhou, J. (2009) Chemical Characteristics of Submicron Particles in Winter in Xi’an. Aerosol and Air Quality Research, 9, 80-93. http://dx.doi.org/10.4209/aaqr.2008.10.0050
- Martin, S.T., Hung, H.M., Park, R.J., Jacob, D.J., Spurr, R.J.D., Chance, K.V. and Chin, M. (2004) Effects of the Phy- sical State of Tropospheric Ammonium-Sulfate-Nitrate Particles on Global Aerosol Direct Radiative Forcing. Atmospheric Chemistry and Physics, 4, 183-214.
- Wang, J., Hoffmann, A.A., Park, R.J., Jacob, D.J. and Martin, S.T. (2008) Global Distribution of Solid and Aqueous Sulfate Aerosols: Effect of the Hysteresis of Particle Phase Transitions. Journal of Geophysical Research: Atmospheres, 113, Published Online. http://dx.doi.org/10.1029/2007JD009367
- Wang, J., Jacob, D.J. and Martin S.T. (2008) Sensitivity of Sulfate Direct Climate Forcing to the Hysteresis of Particle Phase Transitions. Journal of Geophysical Research: Atmospheres, 113, Published Online. http://dx.doi.org/10.1029/2007JD009368
- Köhler, H. (1936) The Nucleus in and Growth of Hygroscopic Droplets. Transactions of the Faraday Society, 32, 1152-1161. http://dx.doi.org/10.1039/tf9363201152
- Petters, M.D. and Kreidenweis, S.M. (2007) A Single Parameter Representation of Hygroscopic Growth and Cloud Condensation Nucleus Activity. Atmospheric Chemistry and Physics, 7, 1961-1971. http://dx.doi.org/10.5194/acp-7-1961-2007
- Wex, H., Hennig, T., Salma, I., Ocskay, R., Kiselev, A., Henning, S., Massling, A., Wiedensohler, A. and Stratmann, F. (2007) Hygroscopic Growth and Measured and Modeled Critical Super-Saturations of an Atmospheric HULIS Sample. Geophysical Research Letters, 34, Published Online. http://dx.doi.org/10.1029/2006GL028260
- Andreae, M.O. and Rosenfeld, D. (2008) Aerosol-Cloud-Precipitation Interactions, Part 1, The Nature and Sources of Cloud-Active Aerosols. Earth-Science Reviews, 89, 13-41. http://dx.doi.org/10.1016/j.earscirev.2008.03.001
- Gunthe, S.S., King, S.M., Rose, D., Chen, Q., Roldin, P., Farmer, D.K., Jimenez, J.L., Artaxo, P., Andreae, M.O., Martin, S.T. and Pöschl, U. (2009) Cloud Condensation Nuclei in Pristine Tropical Rainforest Air of Amazonia: Size-Re- solved Measurements and Modeling of Atmospheric Aerosol Composition and CCN Activity. Atmospheric Chemistry and Physics, 9, 7551-7575. http://dx.doi.org/10.5194/acp-9-7551-2009
- Tijjani, B.I., Aliyu, A. and Shuaibu, F. (2013) The Effect of Relative Humidity on Continental Polluted Aerosols. FJNAS (Fire Journal of Natural and Applied Sciences), 1, 116-138.
- Kammermann, L., Gysel, M., Weingartner, E. and Baltensperger, U. (2010) 13-Month Climatology of the Aerosol Hygroscopicity at the Free Tropospheric Site Jungfraujoch (3580 m a.s.l.). Atmospheric Chemistry and Physics, 10, 10717-10732. http://dx.doi.org/10.5194/acp-10-10717-2010
- Hess, M., Koepke, P. and Schult, I. (1998) Optical Properties of Aerosols and Clouds: The Software Package OPAC. Bulletin of the American Meteorological Society, 79, 831-844.
- Chylek, P. and Wong, J. (1995) Effect of Absorbing Aerosols on Global Radiation Budget. Geophysical Research Letters, 22, 929-931.
- Segan, C. and Pollack, J. (1967) Anisotropic Non-Conservative Scattering and the Clouds of Venus. Journal of Geophysical Research, 72, 469-477. http://dx.doi.org/10.1029/JZ072i002p00469
- Penner, J.E., Dickinson, R.E. and O’Neil, C.A. (1992) Effects of Aerosol from Biomass Burning on the Global Radiation Budget. Science, 256, 1432-1434. http://dx.doi.org/10.1126/science.256.5062.1432
- Randles, C.A., Russell, L.M. and Ramaswamy, V. (2004) Hygroscopic and Optical Properties of Organic Sea Salt Ae- rosol and Consequences for Climate Forcing. Geophysical Research Letters, 31, Published Online. http://dx.doi.org/10.1029/2004GL020628
- Sjogren, S., Gysel, M., Weingartner, E., Baltensperger, U., Cubi-son, M.J., Coe, H., Zardini, A.A., Marcolli, C., Krieger, U.K. and Peter, T.( 2007) Hygroscopic Growth and Water Uptake Kinetics of Two-Phase Aerosol Particles Consis- ting of Ammonium Sulfate, Adipic and Humic acid Mixtures. Journal of Aerosol Science, 38, 157-171. http://dx.doi.org/10.1016/j.jaerosci.2006.11.005
- Stokes, R.H. and Robinson, R.A. (1966) Interactions in Aqueous Nonelectrolyte Solutions. I. Solute-Solvent Equilibria. The Journal of Physical Chemistry, 70, 2126-2130. http://dx.doi.org/10.1021/j100879a010
- Meyer, N.K., Duplissy, J., Gysel, M., Metzger, A., Dommen, J., Weingartner, E., Alfarra, M.R., Prevot, A.S.H., Fle- tcher, C., Good, N., McFiggans, G., Jonsson, A.M., Hallquist, M., Baltensperger, U. and Ristovski, Z.D. (2009) Analysis of the Hygroscopic and Volatile Properties of Ammonium Sulphate Seeded and Unseeded SOA Particles. Atmospheric Chemistry and Physics, 9, 721-732. http://dx.doi.org/10.5194/acp-9-721-2009
- Stock, M., Cheng, Y.F., Birmili, W., Massling, A., Wehner, B., Muller, T., Leinert, S., Kalivitis, N., Mihalopoulos, N. and Wiedensohler, A. (2011) Hygroscopic Properties of Atmospheric Aerosol Particles over the Eastern Mediterranean: Implications for Regional Direct Radiative Forcing under Clean and Polluted Conditions. Atmospheric Chemistry and Physics, 11, 4251-4271. http://www.atmos-chem-phys.net/11/4251/2011/ http://dx.doi.org/10.5194/acp-11-4251-2011
- Duplissy J., DeCarlo, P.F., Dommen, J., Alfarra, M.R., Metzger, A., Barmpadimos, I., Prevot, A.S.H., Weingartner, E., Tritscher, T., Gysel, M., Aiken, A.C., Jimenez, J.L., Canagaratna, M.R., Worsnop, D.R., Collins, D.R., Tomlinson, J. and Baltensperger, U. (2011) Relating Hygroscopicity and Composition of Organic Aerosol Particulate Matter. Atmos- pheric Chemistry and Physics, 11, 1155-1165. http://www.atmos-chem-phys.net/11/1155/2011/ http://dx.doi.org/10.5194/acp-11-1155-2011
- Meier, J., Wehner, B., Massling, A., Birmili, W., Nowak, A., Gnauk, T., Bruggemann, E., Herrmann, H., Min, H. and Wiedensohler, A. (2009) Hygroscopic Growth of Urban Aerosol Particles in Beijing (China) during Wintertime: A Comparison of Three Experimental Methods. Atmospheric Chemistry and Physics, 9, 6865-6880. http://www.atmos-chem-phys.net/9/6865/2009/ http://dx.doi.org/10.5194/acp-9-6865-2009
- Tijjani, B.I. and Uba, S. (2013) The Effect of Hygroscopic Growth on Urban Aerosols. The International Institute for Science, Technology and Education (IISTE), 25, 58-75.
- Tijjani, B.I. and Uba, S. (2013) The Effect of Hygroscopic Growth on Desert Aerosols. Advances in Applied Science Research, 4, 465-478.
- Tijjani, B.I. (2013) The Effect of Soot and Water Soluble on the Hygroscopicity of Urban Aerosols. Advances in Physics Theories and Applications, 26, 52-72.
- Tijjani, B.I. (2013) The Effect of Water Solubles on the Hygroscopicity of Urban Aerosols. International Journal of Computational Engineering Research (IJCER), 03, 45-60.
- Tijjani, B.I., Aliyu, A. and Shuaibu, F. (2013) The Effect of Hygroscopic Growth on Continental Aerosols. Open Jour- nal of Applied Sciences, 3, 381-392. http://dx.doi.org/10.4236/ojapps.2013.36048
- Sheridan, P.J., Delene, D.J. and Ogren, J.A. (2001) Four Years of Continuous Surface Aerosol Measurements from the Department of Energy’s Atmospheric Radiation Measurement Program Southern Great Plains Cloud and Radiation Testbedsite. Journal of Geophysical Research: Atmospheres, 106, 20735-20747. http://dx.doi.org/10.1029/2001JD000785
- Sullivan, R.C., Moore, M.J.K., Petters, M.D., Kreidenweis, S.M., Roberts, G.C. and Prather, K.A. (2009) Effect of Chemical Mixing State on the Hygroscopicity and Cloud Nucleation Properties of Calcium Mineral Dust Particles. At- mospheric Chemistry and Physics, 9, 3303-3316. http://dx.doi.org/10.5194/acp-9-3303-2009
- Rose, D., Gunthe, S.S., Mikhailov, E., Frank, G.P., Dusek, U., Andreae, M.O. and Pöschl, U. (2008) Calibration and Measurement Uncertainties of a Continuous-Flow Cloud Condensation Nuclei Counter (DMT-CCNC): CCN Activation of Ammonium Sulfate and Sodium Chloride Aerosol Particles in Theory and Experiment. Atmospheric Chemistry and Physics, 8, 1153-1179. http://dx.doi.org/10.5194/acp-8-1153-2008
- Poschl, U., Rose, D. and Andreae, M.O. (2009) Climatologies of Cloud-Related Aerosols―Part 2: Particle Hygroscopicity and Cloud Condensation Nuclei Activity. In: Heintzenberg, J. and Charlson, R.J., Eds., Clouds in the Perturbed Climate System, MIT Press, Cambridge, 58-72.
- Christensen, S.I. and Petters, M.D. (2012) The Role of Temperature in Cloud Droplet Activation. The Journal of Physical Chemistry A, 116, 9706-9717. http://dx.doi.org/10.1021/jp3064454
- Niedermeier, D., Wex, H., Voigtländer, J., Stratmann, F., Bruggemann, E., Kiselev, A., Henk, H. and Heintzenberg, J. (2008) LACIS-Measurements and Parameterization of Sea-Salt Particle Hygroscopic Growth and Activation. Atmospheric Chemistry and Physics, 8, 579-590. http://dx.doi.org/10.5194/acp-8-579-2008
- Petters, M.D., Wex, H., Carrico, C.M., Hallbauer, E., Massling, A., McMeeking, G.R., Poulain, L., Wu, Z., Kreidenweis, S.M. and Stratmann, F. (2009) Towards Closing the Gap between Hygroscopic Growth and Activation for Secondary Organic Aerosol: Part 2 Theoretical Approaches. Atmospheric Chemistry and Physics, 9, 3999-4009. http://dx.doi.org/10.5194/acp-9-3999-2009
- Liu P.F., Zhao, C.S., Gobel, T., Hallbauer, E., Nowak, A., Ran, L., Xu, W.Y., Deng, Z.Z., Ma, N., Mildenberger, K., Henning, S., Stratmann, F. and Wiedensohler, A. (2011) Hygroscopic Proper Ties of Aerosol Particles at High Relative Humidity and Their Diurnal Variations in the North China Plain. Atmospheric Chemistry Physics Discussion, 11, 2991- 3040. http://dx.doi.org/10.5194/acpd-11-2991-2011
- Swietlicki, E., Zhou, J.C., Covert, D.S., Hameri, K., Busch, B., Vakeva, M., Dusek, U., Berg, O.H., Wiedensohler, A., Aalto, P., Mäkelä, J., Martinsson, B.G., Papaspiropoulos, G., Mentes, B., Frank, G. and Stratmann, F. (2000) Hygroscopic Properties of Aerosol Particles in the North-Eastern Atlantic during ACE-2. Tellus B, 52, 201-227. http://dx.doi.org/10.1034/j.1600-0889.2000.00036.x
- Birmili, W., Nowak, A., Schwirn, K., Lehmann, K., et al. (2004) A New Method to Accurately Relate Dry and Humidified Number Size Distributions of Atmospheric Aerosols. Journal of Aerosol Science, 1, 15-16.
- Kasten, F. (1969) Visibility Forecast in the Phase of Pre-Condensation. Tellus A, 21, 631-635.
- Gysel, M., McFiggans, G.B. and Coe, H. (2009) Inversion of Tandem Differential Mobility Analyser (TDMA) Measurements. Journal of Aerosol Science, 40, 134-151. http://dx.doi.org/10.1016/j.jaerosci.2008.07.013
- Putaud, J.P. (2012) Interactive Comment on “Aerosol Hygroscopicity at IspraEMEP-GAW Station” by M. Adam et al. Atmospheric Chemistry Physics Discussion, 12, C1316-C1322.
- Jeong, M.J., Li, Z., Andrews, E. and Tsay, S.C. (2007) Effect of Aerosol Humidification on the Column Aerosol Optical Thickness over the Atmospheric Radiation Measurement Southern Great Plains Site. Journal of Geophysical Research: Atmospheres, 112, Published Online. http://dx.doi.org/10.1029/2006JD007176
- Doherty,S.J., Quinn, P.K., Jefferson, A., Carrico, C.M., Anderson, T.L. and Hegg, D. (2005) A Comparison and Summary of Aerosol Optical Properties as Observed in Situ from Aircraft, Ship, and Land during ACE-Asia. Journal of Geophysical Research: Atmospheres, 110, Published Online. http://dx.doi.org/10.1029/2004JD004964
- Quinn, P.K., Bates, T.S., Baynard, T., Clarke, A.D., Onasch, T.B., et al. (2005) Impact of Particulate Organic Matter on the Relative Humidity Dependence of Light Scattering: A Simplified Parameterization. Geophysical Research Letters, 32, Published Online. http://dx.doi.org/10.1029/2005GL024322
- Gassó, S., Hegg, D.A., Covert, D.S., Collins, D., Noone, K.J., et al. (2000) Influence of Humidity on the Aerosol Scattering Coefficient and Its Effect on the Upwelling Radiance during ACE-2. Tellus B, 52, 546-567.
- Clarke, A., McNaughton, C., Kapustin, V., Shinozuka, Y., Howell, S., et al. (2007) Biomass Burning and Pollution Aerosol over North America: Organic Components and Their Influence on Spectral Optical Properties and Humidification Response. Journal of Geophysical Research: Atmospheres, 112, Published Online. http://dx.doi.org/10.1029/2006JD007777
- Hänel, G. (1976) The Properties of Atmospheric Aerosol Particles as Functions of Relative Humidity at Thermodyna- mic Equilibrium with Surrounding Moist Air. Advances in Geophysics, 19, 73-188. http://dx.doi.org/10.1016/S0065-2687(08)60142-9
- Ångström, A. (1961) Techniques of Determining the Turbidity of the Atmosphere. Tellus A, 13, 214-223. http://dx.doi.org/10.1111/j.2153-3490.1961.tb00078.x
- King, M.D. and Byrne, D.M. (1976) A Method for Inferring Total Ozone Content from Spectral Variation of Total Op- tical Depth Obtained with a Solar Radiometer. Journal of the Atmospheric Sciences, 33, 2242-2251. http://dx.doi.org/10.1175/1520-0469(1976)033<2242:AMFITO>2.0.CO;2
- Eck, T.F., Holben, B.N., Reid, J.S., Dubovic, O., Smirnov, A., O’Neil, N.T., Slutsker, I. and Kinne, S. (1999) Wavelength Dependence of the Optical Depth of Biomass Burning, Urban, and Desert Dust Aerosols. Journal of Geophysical Research: Atmospheres, 104, 31333-31349.
- Eck, T.F., Holben, B.N., Dubovic, O., Smirnov, A., Slutsker, I., Lobert, J.M., and Ramanathan, V. (2001) Column-In- tegrated Aerosol Optical Properties over the Maldives during the Northeast Monsoon for 1998-2000. Journal of Geophysical Research: Atmospheres, 106, 28555-28566.
- Eck, T.F., Holben, B.N., Ward, D.E., Dubovic, O., Reid, J.S., Smirnov, A., Mukelabai, M.M., Hsu, N.C., O’ Neil, N.T. and Slutsker, I. (2001) Characterization of the Optical Properties of Biomass Burning Aerosols in Zambia during the 1997 ZIBBEE Field Campaign. Journal of Geophysical Research: Atmospheres, 106, 3425-3448. http://dx.doi.org/10.1029/2000JD900555
- Kaufman, Y.J. (1993) Aerosol Optical Thickness and Atmospheric Path Radiance. Journal of Geophysical Research: Atmospheres, 98, 2677-2992. http://dx.doi.org/10.1029/92JD02427
- O’Neill, N.T., Dubovic, O. and Eck, T.F. (2001) Modified Ångström Exponent for the Characterization of Submicrometer Aerosols. Applied Optics, 40, 2368-2375. http://dx.doi.org/10.1364/AO.40.002368
- O’Neill, N.T., Eck, T.F., Smirnov, A., Holben, B.N. and Thulasiraman, S. (2003) Spectral Discrimination of Coarse and Fine Mode Optical Depth. Journal of Geophysical Research: Atmospheres, 198, Published Online.
- Pedros, R., Martinez-Lozano, J.A., Utrillas, M.P., Gómez-Amo, J.L. and Tena, F. (2003) Column-Integrated Aerosol, Optical Properties from Ground-Based Spectro-Radiometer Measurements at Barrax (Spain) during the Digital Airborne Imaging Spectrometer Experiment (DAISEX) Campaigns. Journal of Geophysical Research: Atmospheres, 108, Published Online. http://dx.doi.org/10.1029/2002JD003331
- Kaskaoutis, D.G. and Kambezidis, H.D. (2006) Investigation into the Wavelength Dependence of the Aerosol Optical Depth in the Athens Area. Quarterly Journal of the Royal Meteorological Society, 132, 2217-2234. http://dx.doi.org/10.1256/qj.05.183
- Schmid, B., Hegg, D.A., Wang, J., Bates, D., Redemann, J., Russell, P.B., Livingston, J.M., Jonsson, H.H., Welton, E.J., Seinfeld, J.H., Flagan, R.C., Covert, D.S., Dubovik, O. and Jefferson, A. (2003) Column Closure Studies of Lower Tropospheric Aerosol and Water Vapor during ACE-Asia Using Airborne Sun Photometer and Airborne in Situ and Ship-Based Lidar Measurements. Journal of Geophysical Research: Atmospheres, 108, Published Online. http://dx.doi.org/10.1029/2002JD003361
- Martinez-Lozano, J.A., Utrillas, M.P., Tena, F., Pedros, R., Canada, J., Bosca, J.V. and Lorente, J. (2001) Aerosol Op- tical Characteristics from Summer Campaign in an Urban Coastal Mediterranean Area. IEEE Transactions on Geo- science and Remote Sensing, 39, 1573-1585. http://dx.doi.org/10.1109/36.934089
- Aspens, D.E. (1982) Local-Field Effect and Effective Medium Theory: A Microscopic Perspective. American Association of Physics Teachers, 50, 704-709. http://dx.doi.org/10.1119/1.12734
- Heller, W. (1945) The Determination of Refractive Index of Colloidal Particles by Means of a New Mixture Rule or from Measurements of Light Scattering. Physical Review, 68, 5-10. http://dx.doi.org/10.1103/PhysRev.68.5
- Wang, J. and Martin S.T. (2007) Satellite Characterization of Urban Aerosols: Importance of Including Hygroscopicity and Mixing State in the Retrieval Algorithms. Journal of Geophysical Research: Atmospheres, 112, Published Online. http://dx.doi.org/10.1029/2006JD008078
- Shettle, E.P. and Fenn, R.W. (1979) Models for the Aerosols of the Lower Atmosphere and the Effects of Humidity Variations on Their Optical Properties. Rep. No. AFGL-TR-79-0214, ERP No. 676, Air Force Geophys. Lab., Optical Phys. Div., Hanscom Air Force Base, Mass.
- d’Almeida, G.A., Koepke, P. and Shettle, E.P. (1991) Atmospheric Aerosols: Global Climatology and Radiative Characteristics. A. Deepak, Hampton, 561 pp.
- Lorentz, H.A. (1880) Ueber die Beziehungzwischen der Fortpflanzungsgeschwindigkeit des Lichtes und der Körperdichte. Annalen der Physik, 245, 641-665. http://dx.doi.org/10.1002/andp.18802450406
- Lorenz, L. (1880) Ueber die Refractionconstante. Annual Review of Physical Chemistry, 11, 70-103.
- Schuster, G.L., Dubovik, O. and Holben, B.N. (2006) Angstrom Exponent and Bimodal Aerosol Size Distributions. Journal of Geophysical Research: Atmospheres, 111, Published Online. http://dx.doi.org/10.1029/2005JD006328
- Whitby, K. (1978) The Physical Characteristics of Sulfur Aerosols. Atmospheric Environment, 12, 135-159. http://dx.doi.org/10.1016/0004-6981(78)90196-8
- Seinfeld, J.H. and Pandis, S.N. (1998) Atmospheric Chemistry and Physics. Wiley-Inter-Science Publication, Hoboken.
- Fitzgerald, J.W. (1975) Approximation Formulas for the Equilibrium Size of an Aerosol Particle as a Function of Its Dry Size and Composition and Ambient Relative Humidity. Journal of Applied Meteorology, 14, 1044-1049 http://dx.doi.org/10.1175/1520-0450(1975)014<1044:AFFTES>2.0.CO;2
- Tang, I.N. (1996) Chemical and Size Effects of Hygroscopic Aerosols on Light Scattering Coefficients. Journal of Geophysical Research: Atmospheres, 101, 19245-19250. http://dx.doi.org/10.1029/96JD03003
- Liou, K.N. (2002) An Introduction to Atmospheric Radiation. Elsevier, New York, 583 p.










