Open Journal of Applied Sciences
Vol.3 No.2(2013), Article ID:33286,5 pages DOI:10.4236/ojapps.2013.32023
Modelling Absorption Capacity Performance of Hygienic Product
Textile Engineering Laboratory, Monastir University, Monastir, Tunisia
Email: soumaessayeb@yahoo.fr
Copyright © 2013 Soumaya Sayeb et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 3, 2013; revised February 4, 2013; accepted February 12, 2013
Keywords: Model; Absorption Capacity; Hygienic Product; Superabsorbent
ABSTRACT
The performance prediction of hygienic products can be a major advantage for manufacturers. Among the interesting performances to be expected, we find the absorption capacity. This is a parameter governed by the composition of the absorbent core, particularly the fibrous component and the characteristics of the superabsorbent polymer (SAP). Thus, various theoretical models have been established to predict the absorption capacity. All these models have taken into account the nature of the fibrous support and the ratio of superabsorbent polymer. Certainly, other factors, less obvious in their modelling, are involved in determining the performance such as the homogeneity of the mixture formed by the fluff and SAP, the distribution of polymer particles in the entire structure, the porous structure, the shape of the capillary, the nature of the nonwoven webs used, etc. Various theoretical models are proposed here to describe the absorption capacity and we will outline the model which best describes this performance. The experimental test results are discussed to verify if the theoretical model selected can be confirmed.
1. Introduction
Hygienic products have as main component an absorbent core that contains cellulosic fibers from wood pulp (fluff) in which super absorbent particles are spread. The ability of the final product to absorb rapidly and to transport the liquid through the absorbent core is an important requirement. Thus absorbency has been always regarded as one of the most important features desired by consumers in disposable diapers [1-3].
Absorptive capacity is largely determined by the storage capacity and the structure parameters. However, the rate of diffusion of the liquid is influenced by the structure permeability and the capillary shape. The liquid movement in any fibrous structure is influenced by its porosity. The shape of the pores in the fiber structure depends significantly on the type of fiber and the assembly method [4-7]. Based on these findings, Hsieh [5] assumed that the absorption capacity is the ratio between the mass of the liquid absorbed and structure weight before absorption.
Absorption capacity can be considered as:
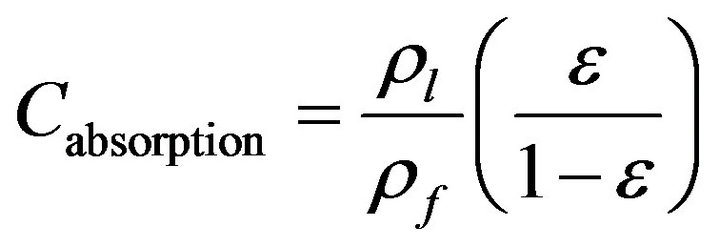 (1)
(1)
where ⍴l is the liquid density, ⍴f is the fiber density and ε is the porosity of the structure.
Nevertheless, Gupta et al. [7] consider the absorption capacity as the sum of the amount of liquid held within the pores and the amount diffused and held within the structure of the fibers. Absorption capacity can be expressed by the following equation:
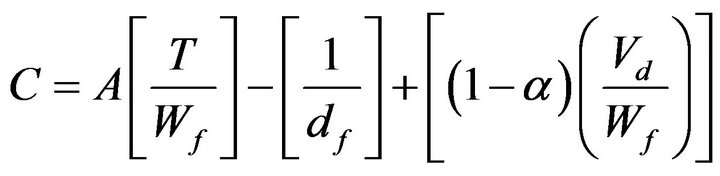 (2)
(2)
with:
C: the absorption capacity of the structure (in cm3/g)A: area structure (cm2)T: thickness of the structure (in cm)Wf: dry fiber weight (in g)df: fiber density (g/cm3)α: the ratio of the increase in volume of a fiber upon wetting to the volume of the liquid diffused into fiber.
Vd: amount of liquid diffused into the structure of the fibers (in cm3).
In this equation (Equation (2)), it was found that the second term is negligible compared to the first. The third term is nearly zero assuming that a fiber swells strictly by exchanging fiber volume with liquid volume. The most important factor in this Equation (2) is therefore the thickness structure [8]. Any factors that affect structure thickness will affect the absorbent capacity. The expression of absorptive capacity is reduced to:
 (3)
(3)
However, the liquid movement in the porous structure is influenced by the capillary forces which in turn are governed by the properties of the liquid (surface tension, viscosity, and density), the fiber surface wetting characteristics, and the geometric configuration of the porous structure [5,9].
Since, it is convenient to divide the mechanism of liquid absorption by a porous structure into 3 basic categories: acquisition, retention and distribution. First, the liquid should be quickly acquired before it is transferred to other parts of the absorbent core. Therefore, sufficient void volume is required for efficient liquid acquisition. Combining super absorbent polymer (SAP) particles with fiber results is an increase of the void volume. Dutkiewicz [4] has established a model expressing the change in the void volume 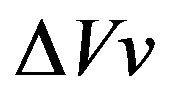 in the absorbent structure:
in the absorbent structure:
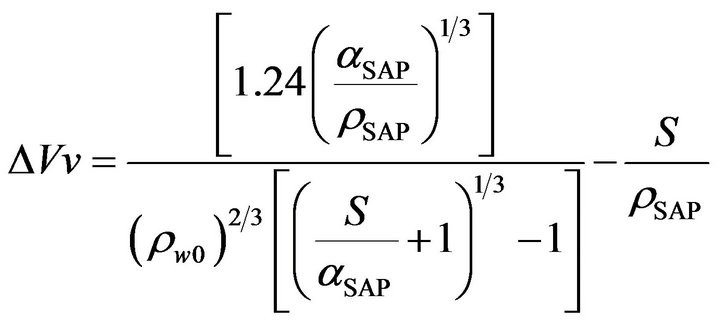 (4)
(4)
with:
αSAP: SAP ratio in the structure (%)ρSAP: SAP density (g/cm3)ρw0: the initial density of the structure (g/cm3)S is saturation of the structure (mL/g).
Equation 4 illustrates many factors that can permit the prediction of the maximum absorption capacity which is the saturation of the absorbent core. In fact it is based on précised parameters referring to the SAP (ρSAP and αSAP) and to the fibrous material (ρw0).
To verify the theoretical model shown above and to decide if this model corresponds to real absorption phenomenon, we made experimental measurements.
2. Materiel and Methods
2.1. Material Charcteristics
This work used bleached soft wood fibre from STORA fluff LKC (mean length 2.7 mm), HySorb B7160 super absorbent polymer based on sodium acrylate (BASF), commercial fibre of viscose (1.7 dtex) and acrylic (1.3 dtex).
2.2. Experiments
Total absorption capacity were realised according to STN2: 117/87 standards for total absorbency measurement. The liquid test used is a 0.9% NaCl solution.
The absorption capacity measures the liquid quantity remained associated to the material after a time of impregnation and draining.
Figure 1 shows the model of the absorbent structure that has been developed. For these structures, we proceeded to the determination of the maximum absorption capacity. The maximum of absorption capacity determine the saturation of the structure.
To demonstrate the previously described model (Equation (4)), we perform two sets of tests. For both sets of tests, all parameters (ρSAP, αSAP and ρw0) will be varied. For first set, density will be varied by changing the total compression of the structure. In second one, it is varied by changing the nature of the fibers used.
3. Results and Discussion
3.1. SAP Ratio and Absorbent Structure Density Variation
For these tests, we will vary the super absorbent polymer ratio and the density of the absorbent structure. The last parameter will be varied by changing the compression of the structure i.e. the structure thickness.
We conducted a series of 18 tests where the ratio of super absorbent polymer is varied according to 6 levels and the compression according to 3 levels. Table 1 shows the values corresponding to each level.
Figure 1. Model of the absorbent structure tested.
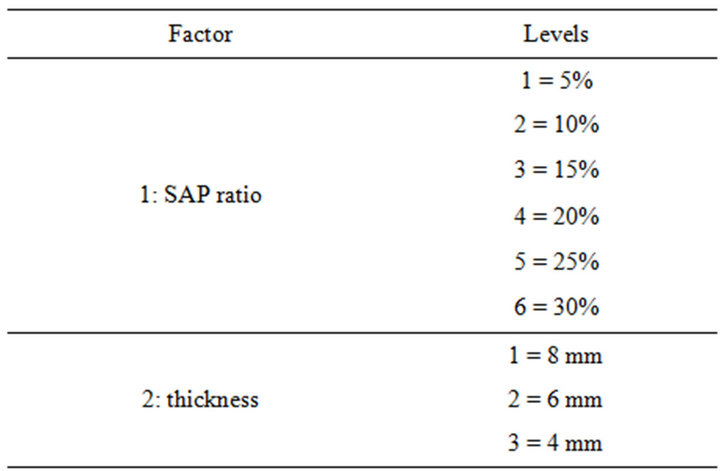
Table 1. Levels factor.
The 18 tests were conducted by combining different levels of each factor. Table 2 shows the distribution of tests according to the previously established levels.
Once the saturation of the various samples was determined, we proceeded to calculate the variation of the void volume. The obtained results are shown in Figure 2. It illustrates the variation of void volume as a function of SAP ratio and thus for different levels of compression that has been fixed.
These curves reveal the effect of compression on the void volume within the porous structure. An increase in compression causes a considerable decrease in interstitial space between fibers. It also reduces the size of capillaries and thus a decline of the structure porosity, which explains the observed results.
Moreover, we note that for different levels of compression, the fibrous structure shows an increase in the interstitial space due to the augmentation in SAP ratio. Then we note that this volume is practically constant even after the increase in SAP ratio. However, with varying levels of compression, different structures reach an equal maximum of void volume.
This behaviour suggests also that the SAP particles swell considerably and generate a decrease of the permeability of the absorbent core and thus resulting in a
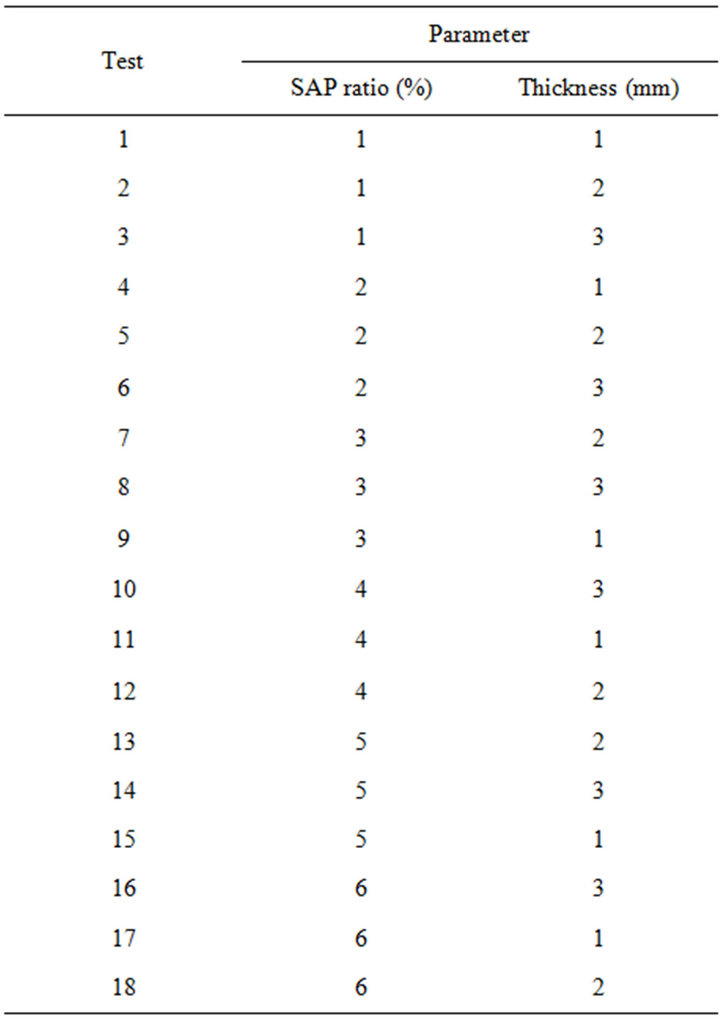
Table 2. Tests plan.
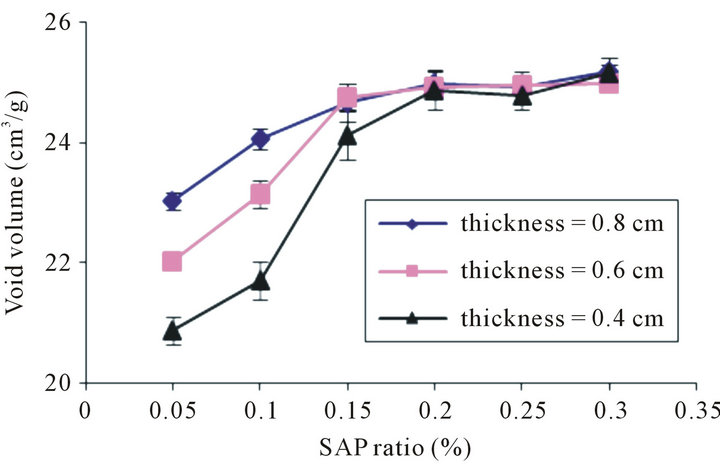
Figure 2. Variation of void volume in absorbent structure in function of thickness.
reduction in the void volume. Consequently, the fibrous structure limits its absorption.
Therefore, structure saturation occurs beyond a certain threshold of SAP ratio. This threshold value inhibits any absorption or liquid diffusion through the absorbent structure.
3.2. Fiber Structure Variation
During these experiments, we proceeded to the variation of the structure density by changing the nature of the fibrous support. SAP ratio is also varied.
The experimental procedure adopted is as follows: for different SAP ratios, we inserted viscose and acrylic fiber in to the mixture of fluff. As result, density structure (ρw0) and SAP ratio (αSAP) are varied.
Here, the experiments were carried out in two stages. The first corresponds to structure prepared with an absorbent core made of mixtures of fluff + (viscose or acrylic) fiber which are realized according to a fixed ratio 80% fluff + 20% (viscose or acrylic). Obviously, to determine the saturation of the absorbent core, SAP ratio is varied.
The second stage will be conducted as follows: we fixed the SAP ratio (αSAP = constant = 25%) and we varied the mixture ratios constituting the fibrous support. It is to find the fibrous structure that offers best distribution of void volume which leads to improved acquisition and consequently allows less saturation of the absorbent core.
Results are described in Figure 3. The curves illustrate the variation of void volume within the different structures realized with SAP ratio increase.
We notice that the SAP ratio increase results in void volume augmentation within the absorbent core until reaching a certain threshold of SAP. Indeed, the curves start with an initial growth phase for which any increase in SAP ratio generates a rise in the void volume, then these curves show a phase of stabilization where void volume remains unchanged.
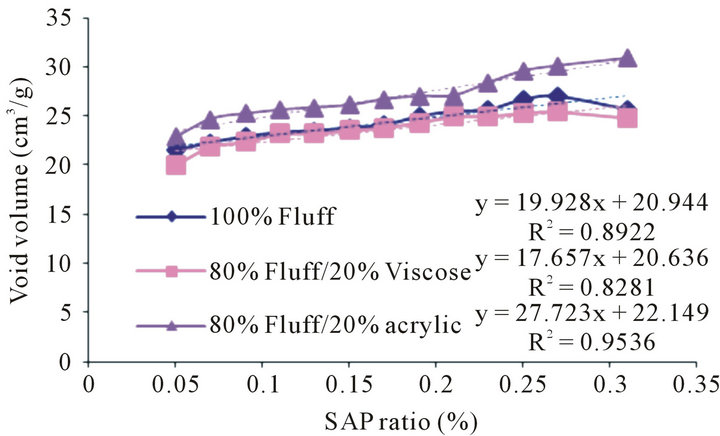
Figure 3. Variation of void volume in absorbent structure in function of fiber composition of the absorbent structure.
However, we observe that the fibrous structure, which provides better void volume while increasing SAP ratio, consists of a mixture of fluff + acrylic. The structure that provides the minimum of void volume is made by a fibrous core containing fluff + viscose.
Indeed, we confirm that adding acrylic fiber to fluff diminishes the contact between the swollen SAP particles and inhibits the occurrence of the phenomenon of gel blocking resulting from the decrease in void volume within the absorbent core. This points out the importance of physical structure: acrylic which is more resilient than fluff is not prone to clotting in wet state, indeed and due to this property, physical structure is kept after wet deformation [10]. Consequently the distribution of liquid is improved.
When we fixed SAP ratio (αSAP = constant = 25%) and vary mixtures ratio, we obtain Figure 4.
Figure 4 shows that fixing the SAP ratio results in a maximum of void volume in both structures consisting of a mixture 80% fluff + 20% (acrylic or viscose). As mentioned, this ratio provides a better arrangement of SAP particles within the absorbent core and consequently larger voids volume that promotes better absorption. Nevertheless, acrylic fiber improves absorption as compared to viscose due to the ability of acrylic to form the physical structure more resilient and stable in the wet state.
4. Conclusions
Different models describing the absorption capacity performance within a fibrous structure are presented. The key parameters needed to predict this performance are: the superabsorbent polymer ratio, the structure compression, and the fiber support properties. Indeed, these parameters affect the performances: super absorbent polymer and fibrous support permit the absorption of the liquid, pore volume presented in the structure assure the acquisition of liquid.
We selected a model that describes the variation of void volume in the structure during liquid absorption: it
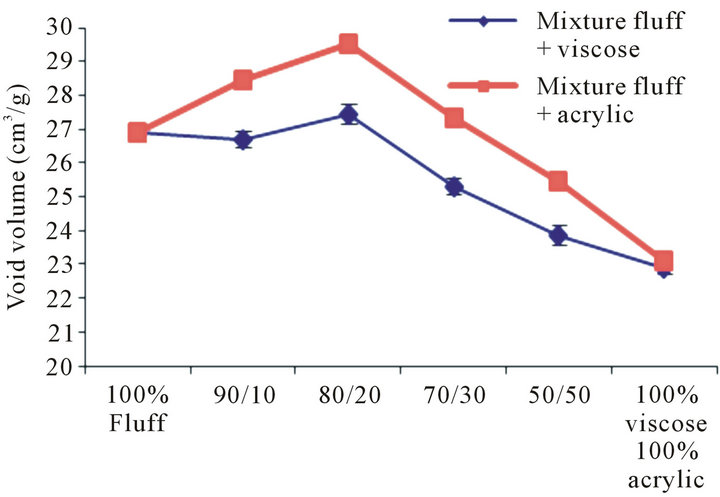
Figure 4. Variation of void volume in absorbent structure in function of fiber mixture ratios (αSAP = 25%).
illustrates the changes that occur in the structure due to the swelling of the superabsorbent polymer particles. Through the experiments carried out in this study, we tried to verify the theoretical model and to decide if this model corresponds to real absorption phenomenon.
The investigated tests revealed a high correlation between the experimental tests conducted and the results described by the model. Thus, for a structure containing fixed super absorbent ratio, the incorporation of synthetic fibers such us acrylic can significantly improve the behaviour of the fiber structure and therefore the absorption. The gel blocking occurrence is largely limited.
REFERENCES
- R. Saminathan and B. W. Steven, “Modern Diaper Technology,” Tappi Journal, Vol. 79, No. 6, 1996, pp. 173- 177.
- EDANA, “Absorbent Hygiene Products, Training Course: Baby Diapers, Sanitary Protection and Adult Incontinence,” European Disposables and Nonwovens Association, Vol. 1, 1997, pp. 25-35,42-51.
- P. Wiertz, “Sustainability Report 2007-2008: Absorbent hygiene Products,” 2011. http://www.edana.org/docs/default-source/default-document-library/sustainability-report-absorbent-hygiene-products-2007-2008.pdf?sfvrsn=2
- J. Dutkiewicz, “Some Abvances in Nonwovens Structures for Absorbency, Confort and Aesthetics,” Autex Research Journal, Vol. 2, No. 3, 2002, pp. 153-165.
- B. S. Gupta and C. J. Hong, “Changes in Web Dimensions during Fluid Uptake and the Impact on Absorbency,” Tappi Journal, Vol. 77, No. 12, 1994, pp. 181- 188.
- L. Darry, “Nonwovens Containing Immobilized Super Absorbent Polymer Particles,” International Nonwovens Journal, Vol. 12, No. 3, 2003, pp. 35-39.
- M. G. Kamath and A. Dahiya, “Absorption Properties,” 2004. http://www.engr.utk.edu/mse/Textiles/Absorption.htm
- Y. L. Hsieh, “Liquid Transport in Fabric Structures,” Textile Research Journal, Vol. 65, No. 5, 1995, pp. 299- 307. doi:10.1177/004051759506500508
- A. Patnaik, R. S. Rengasamy, et al., “Wetting and Wicking in Fibrous Materials,” Textile Progress, Vol. 38, No. 1, 2006, pp. 1-9. doi:10.1533/jotp.2006.38.1.1
- C. Rosinskaya, “Effect of Synthetic Fibres on Absorption Properties of Pads,” International Nonwovens Journal, Vol. 11, No. 2, 2002, pp. 11-17.

