Received 21 March 2016; accepted 30 May 2016; published 2 June 2016

ABSTRACT

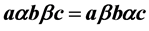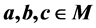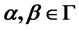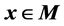Let M be a 2-torsion free semiprime G-ring with involution satisfying the condition that (and). In this paper, we will prove that if a non-zero Jordan G^*-derivation d on M satisfies for all and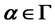, then.

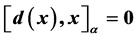Keywords:

G-Ring M with Involution, Jordan G^*-Derivation, Commutative G-Ring

1. Introduction

The notion of G-ring was introduced as a generalized extension of the concept on classical ring. From its first appearance, the extensions and the generalizations of various important results in the theory of classical rings to the theory of G-rings have attracted a wider attention as an emerging field of research to enrich the world of algebra. A good number of prominent mathematicians have worked on this interesting area of research to develop many basic characterizations of G-rings. Nobusawa [1] first introduced the notion of a G-ring and showed that G-rings are more general than rings. Barnes [2] slightly weakened the conditions in the definition of G-ring in the sense of Nobusawa. Barnes [2] , Luh [3] , Kyuno [4] , Hoque and Pual [5] - [7] , Ceven [8] , Dey et al. [9] [10] , Vukman [11] and others obtained a large number of important basic properties of G-rings in various ways and developed more remarkable results of G-rings. We start with the following necessary introductory definitions.

Let M and G be additive abelian groups. If there exists an additive mapping 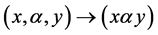of 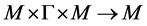which satisfies the conditions:

1),

2),

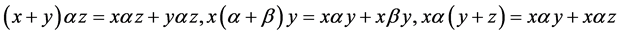3)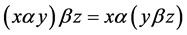, then M is called a G-ring [2] . Every ring M is a G-ring with M = G. However a G- ring need not be a ring. Let M be a G-ring. Then M is said to be prime if 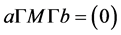with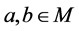, implies 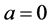or and semiprime if with implies. Furthermore, M is said to be a commutative G-ring if for all and. Moreover, the set is called the center of the G-ring M. If M is a G-ring, then is known as the commutator of x and y with respect to, where and. We make the following basic commutator identities:

(1)

(2)

for all and. Now, we consider the following assumption:

A......., for all and.

According to assumption (A), the above commutator identities reduce to and, which we will extensively used.

During the past few decades, many authors have studied derivations in the context of prime and semiprime rings and G-rings with involution [11] - [14] . The notion of derivation and Jordan derivation on a G-ring were defined by [15] . Let M be G-ring. An additive mapping is called a derivation if for all and. An additive mapping is called a Jordan derivation if for all and.

Definition 1 [16] . An additive mapping on a G-ring M is called an involution if and for all and. A G-ring M equipped with an involution is called a G-ring M with involution.

Definition 2. An element x in a G-ring M with involution is said to be hermitian if and skew-hermi- tian if. The sets of all hermitian and skew-hermitian elements of M will be denoted by and, respectively.

Example 1. Let F be a field, and be a set of all diagonal matrices of order 2, with respect to the usual operation of addition and multiplication on matrices and the involution * on be defined by

with, then we get and.

Definition 3. An additive mapping is called a -derivation if for all and.

To further clarify the idea of -derivation, we give the following example.

Example 2. Let R be a commutative ring with characteristic of R equal 2. Define and, then M and are abelian groups under addition of matrices and M is a G-ring under multiplication of matrices.

Define a mapping by.

To show that d is a -derivation, let

, ,

then

Now,

since, this implies that then . Hence, d is a -derivation.

Definition 4. An additive mapping is called Jordan -derivation if for all and.

Every -derivation is a Jordan -derivation, but the converse in general is not true as shown by the following example

Example 3. Let M be a G-ring with involution and let such that and for all and, but for some such that.

Define a mapping by for all and. To show that d is a Jordan -derivation, we have on the one hand that

(3)

for all and. On the other hand,

(4)

for all and. If we compare Equations ((3), (4)), we get

then after reduction we get that d is a Jordan -derivation. Now to show that d is not a -derivation, we have on the one hand that

(5)

for all and. On the other hand

(6)

for all and. If we compare Equations ((5), (6)), we get

then after reduction we get that d is not a -derivation.

In this paper we will prove that if a non-zero Jordan -derivation d of a 2-torsion free semiprime G-ring M with involution satisfies for all and, then.

2. The Relation between Jordan G^*-Derivation and on Semiprime G-Ring M with Involution

To prove our main results we need the following lemmas.

Lemma 1. Let M be a 2-torsion free semiprime G-ring with involution and be a Jordan - derivation which satisfies for all and, then for all and.

Proof. We have

(7)

for all and. Putting for x in (7), we get

(8)

for all and. Therefore,

for all and. Setting in the above relation, we get

(9)

for all and, because of

(10)

for all and. According to (9) and (10), we get

(11)

for all and. Then from relation (11)

for all and. Since, then, and hence from the above relation

for all and. Therefore,

for all and. Then by using assumption (A), we obtain

(12)

for all and. And

(13)

for all and. Then from (13),

for all and. Since, then from the above relation

hence by using assumption (A), we obtain

(14)

for all and. Therefore,

(15)

for all and. Then from relation (15),

for all and. By using relation (15) and assumption (A), we get

(16)

for all and. Since M is 2-torsion free, we get

(17)

for all and. Right multiplication of (17) by and using assumption (A), we get

(18)

for all and. By semiprimeness of M, we have

(19)

for all and. Left multiplication of (19) by z yields

(20)

for all and. By semiprimeness of M again, we get for all and. W

Lemma 2 Let M be a 2-torsion free semiprime G-ring with involution and be a Jordan - derivation which satisfies for all and, then for all and.

Proof. Putting for x in (7),

for all and. By using Lemma (1), we get

(21)

for all and. Replacing x by and y by yields

(22)

for all and. Setting, we get

(23)

for all and. But

(24)

for all and. So then from (23) and (24), we get

for all and. Hence,

for all and. Since, then, hence from the above relation,

(25)

for all and. Therefore,

(26)

for all and. Since, we obtain

(27)

for all and. Then from relation (27),

for all and. By using relation (27) again,

(28)

for all and. Since M is 2-torsion free, we get

(29)

for all and. Right multiplication by z yields

(30)

for all and. By semiprimeness of M, we therefore get for all and. W

Remark 1 [17] . A G-ring M is called a simple G-ring if and its ideals are 0 and M.

Remark 2. Let M be a 2-torsion free simple G-ring with involution, then every can be uniquely represented in the form where and.

Proof. Define, , since 2M is an ideal of M and M is simple, it implies that. So for every, makes sense and so we can write

Now

hence

and

hence

Therefore

hence. Let, then and, so and. Therefore which implies that, so. Thus. Hence implies that where and. W

Theorem 1. Let M be a 2-torsion free semiprime G-ring with involution and be a Jordan - derivation which satisfies for all and and or for all, and, then for all and.

Proof. Assume that for all, and. By using Lemma (1), we have

(31)

for all and. For, putting for h in (31) yields

for all and. By using relation (31), we obtain

(32)

for all and. Since for all, then replace by in (32), to get

(33)

for all, and. By using Lemma (2), we have

(34)

for all and. According to relations (33) and (34), we get

for all and. By using Lemma (2), we get

(35)

for all and. Then from relation (35),

for all, and. Therefore since, we obtain

(36)

for all, and. Hence,

(37)

for all, and. Therefore,

for all, and. Then by using (37), we get

(38)

for all, and. Since M is 2-torsion free, we get

(39)

for all, and. Right multiplication of relation (39) by z yields

(40)

for all, and. By semiprimeness of M, we get

(41)

for all, and. Putting s for x and h for y in relation (21), we get

(42)

for all, and. Comparing relations (41) and (42), we get

(43)

for all, and. Since for all, then from relation (43), we obtain

(44)

for all, and. Then

(45)

for all, and. Since for all, and, then from relation (45), we get

(46)

for all, and. Hence

(47)

for all, and. Then from relation (47),

for all, and. Then by using (47), we get

(48)

for all, and. Since M is 2-torsion free, we get

(49)

for all, and. Right multiplication of the relation (49) by z we get

(50)

for all, and. By semiprimeness of M, we get

(51)

for all, and. To prove, since M is 2-torsion free, we only show

(52)

for all and. By using Remark 2, we have for all and that for all and. Therefore

for all, and. Hence

(53)

for all, and. By using Lemma (1), Lemma (2) and relation (41), (51), we get

Now assume for all, and. Since for all, then we get

(54)

for all, and. Then from relation (54), we obtain

(55)

for all, and. Since for all, and, then from relation (55), we get

(56)

for all, and. Hence

(57)

for all, and. Then from relation (57),

for all, and. Then by using relation (57) we get

(58)

for all, and. Since M is 2-torsion free, we get

(59)

for all, and. Right multiplication of relation (59) by z yields

(60)

for all, and. By semiprimeness of M, we get

(61)

for all, and. Comparing relations (42) and (61), we get

(62)

for all, and. Since for all, then from (62), we obtain

(63)

for all, and. Then,

(64)

for all, and. Since for all, and, then from relation (64), we get

(65)

for all, and. Hence

(66)

for all, and. Then from relation (66)

for all, and. Then by using (66) we get

(67)

for all, and. Since M is 2-torsion free, we get

(68)

for all, and. Right multiplication of relation (68) by z yields

(69)

for all, and. By semiprimeness of M, we get

(70)

for all, and. Therefore, by using Lemma (1), Lemma (2) and relation (61), (70), we get a similar result as the first assumption for all and, and hence the proof of the theorem is complete. W

Acknowledgements

This work is supported by the School of Mathematical Sciences, Universiti Sains Malaysia under the Short-term Grant 304/PMATHS/6313171.

Cite this paper

Ali Kareem,Hajar Sulaiman,Abdul-Rahman Hameed Majeed, (2016) Jordan Γ*-Derivation on Semiprime Γ-Ring M with Involution. Advances in Linear Algebra & Matrix Theory,06,40-50. doi: 10.4236/alamt.2016.62006

References