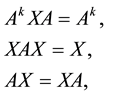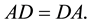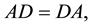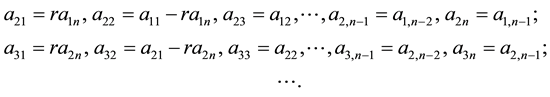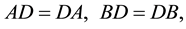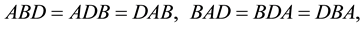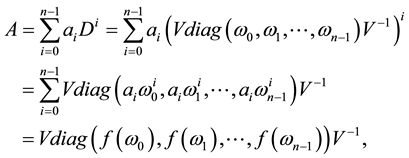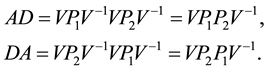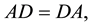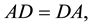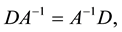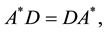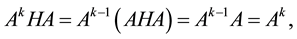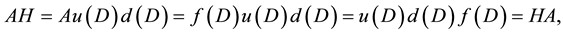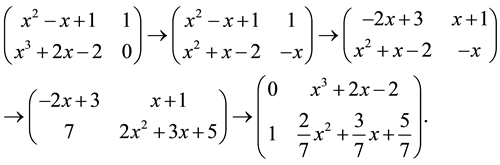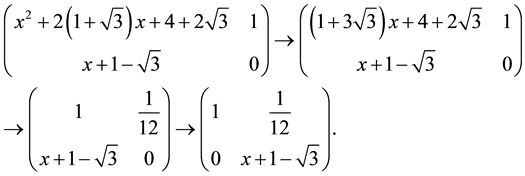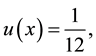Advances in Linear Algebra & Matrix Theory
Vol.05 No.02(2015), Article ID:57509,7 pages
10.4236/alamt.2015.52006
The Discriminance for FLDcircr Matrices and the Fast Algorithm of Their Inverse and Generalized Inverse
Xue Pan, Mei Qin
College of Science, University of Shanghai for Science and Technology, Shanghai, China
Email: xiaoxuehe1126@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 May 2015; accepted 23 June 2015; published 29 June 2015
ABSTRACT
This paper presents a new type of circulant matrices. We call it the first and the last difference r-circulant matrix (FLDcircr matrix). We can verify that the linear operation, the matrix product and the inverse matrix of this type of matrices are still FLDcircr matrices. By constructing the basic FLDcircr matrix, we give the discriminance for FLDcircr matrices and the fast algorithm of the inverse and generalized inverse of the FLDcircr matrices.
Keywords:
FLDcircr Matrix, Discriminance, Diagonalization, Inverse, Generalized Inverse

1. Introduction
Circulant matrix plays an important role in the matrix theory, its special structure and properties have been widely used in applied mathematics, physics, modern engineering, and so on [1] -[6] . There have been many new circulant matrices come fordward [7] -[12] . In this paper we will firstly put forward the concept of the FLDcircr matrix and the basic FLDcircr matrix. The sum, the difference, the product, the inverse and the adjoint matrix of this type of matrices are still FLDcircr matrices. Then, we will give five discriminance for FLDcircr matrix by constructing the basic FLDcircr matrix. At last, we will discuss the fast algorithm of the inverse and generalized inverse of the FLDcircr matrix and give the numerical example. In this paper, we just study the square matrices in complex field.
2. Definition of the FLDcircr Matrix
Definition 2.1 For a square matrix A of order n, if its form is
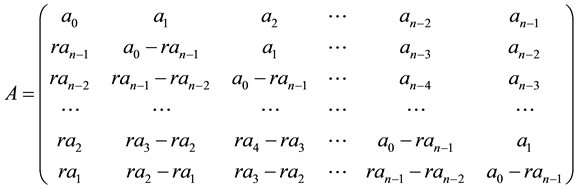 ,
,
We call it the FLDcircr matrix, and denote shortly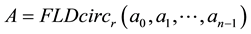 .
.
Definition 2.2 Let D is the basic FLDcircr matrix of order n, that is
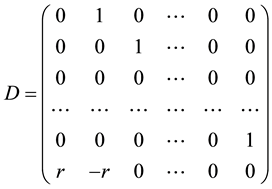 .
.
We obtain 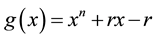 is the characteristic polynomial of D,
is the characteristic polynomial of D, 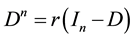 , we specify
, we specify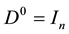 .
.
From the definition of FLDcircr matrix, we can prove the following proposition.
Proposition 2.3 If A and B are FLDcircr matrices, then A + B, A − B and kA are both FLDcircr matrices, for any k belongs to the complex field.
Definition 2.4 Let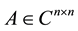 ,the index of A is the least nonnegative integer k such that
,the index of A is the least nonnegative integer k such that , we note it as
, we note it as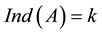 . If A is nonsingular, then
. If A is nonsingular, then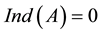 ; if A is singular, then
; if A is singular, then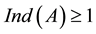 .
.
Definition 2.5 Let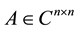 , if there is
, if there is 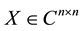 which satisfies
which satisfies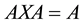 ,
, 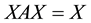 at the same time, we named X as the reflexive generalize inverse of A, we note it as
at the same time, we named X as the reflexive generalize inverse of A, we note it as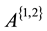 .
.
Definition 2.6 Let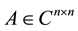
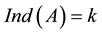
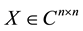
Then we denote X as the Drazin inverse of A, note it as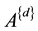
Lemma 2.7 If polynomial matrix 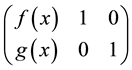
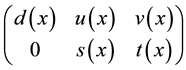
tary row transformation, then we have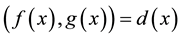
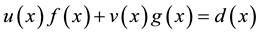
3. The Discriminance of the FLDcircr Matrix
Theorem 3.1 A is an FLDcircr matrix if and only if A is of the following form
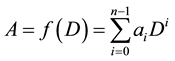
For some polynomial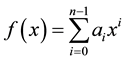
Proof. By the Definition 2.1 and Definition 2.2, we get this result.
Theorem 3.2 A is an FLDcircr matrix if and only if AD = DA, D is the basic FLDcircr matrix.
Proof. 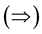

Due to
It follows that
We obtain
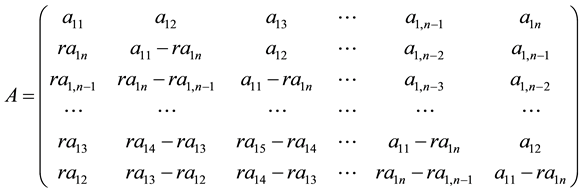
So A is an FLDcircr matrix.
Corollary 3.3 If A and B are both FLDcircr matrices, then AB and BA are FLDcircr matrices. Furthermore, we get AB = BA.
Proof. Since A and B are FLDcircr matrices, by the Theorem 3.2, we get
Hence
Then, AB and BA are both FLDcircr matrices.
From Theorem 3.1, we have
4. The Diagonalization of the FLDcircr Matrix
First, we consider the diagonalization of the basic FLDcircr matrix D.
For the characteristic polynomial 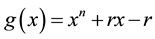
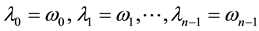
Let
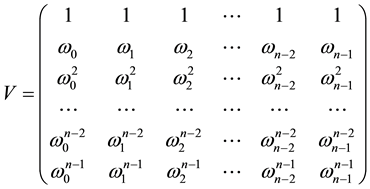
Obviously, 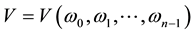
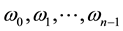
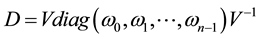
Next, we study the diagonalization of general FLDcircr matrix A.
From Theorem 3.1 and Equation (2), we obtain
The eigenvalues of A are
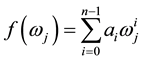
Theorem 4.1 A is an FLDcircr matrix if and only if 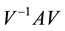
Proof. 
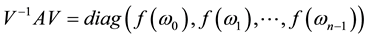
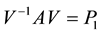
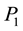
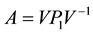
Let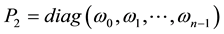
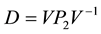
Thus
For 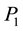
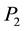
hence, A is an FLDcircr matrix.
Theorem 4.2 A is a nonsingular FLDcircr matrix if and only if the eigenvalues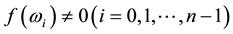
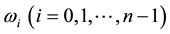
Proof. 
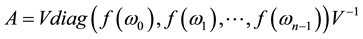
where 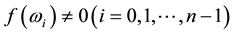
So
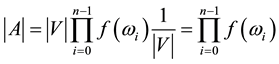
Hence, if A is a nonsingular FLDcircr matrix, we have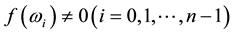
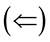
Then
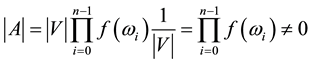
So A is nonsingular.
5. The Fast Algorithm of the Inverse and Generalized Inverse of the FLDcircr Matrix
Theorem 5.1 If A is a nonsingular matrix, then A is an FLDcircr matrix if and only if 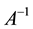
Proof. 
Hence
That is to say 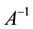
Corollary 5.2 If A is a nonsingular FLDcircr matrix, then 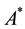
Proof. For A is an FLDcircr matrix, we have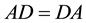
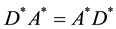
Due to
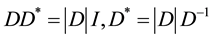
Thus
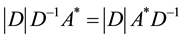
Hence
Then 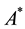
Theorem 5.3 If A is an FLDcircr matrix, then A is nonsingular if and only if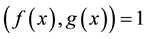
Proof. If A is a nonsingular FLDcircr matrix, from Theorem 4.2, we have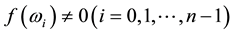
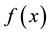
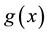
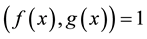
Otherwise, if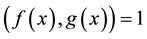
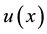
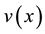
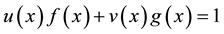
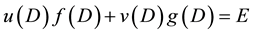
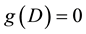
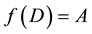
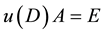

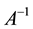
Corollary 5.4 If A is a nonsingular FLDcircr matrix, there exits
Corollary 5.5 A is a singular FLDcircr matrix, there exists an FLDcircr matrix H that satisfies 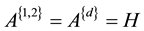
Proof. For A is singular, we get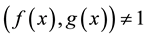
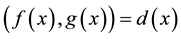
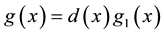
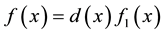
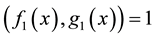
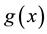
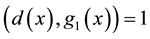
Hence, there exist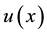
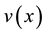

Equation (3) both sides multiplied by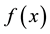
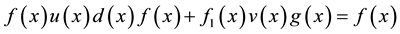
For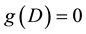
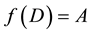
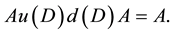
Equation (3) both sides multiplied by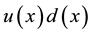
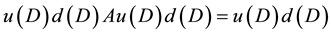
If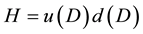
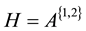
Due to
Hence
From Lemma 2.7 and the proof of Theorem 5.3, Corollary 5.5, we can get the fast algorithm of the inverse and generalized inverse of the FLDcircr matrix. The general steps are as follows:
Step 1 get the greatest common factor 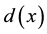
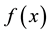
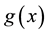
Step 2 If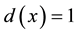
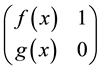
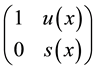
row transformation, then
Step 3 If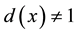
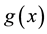
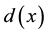
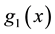
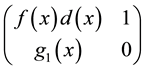
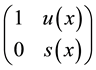
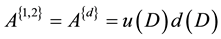
Example 5.1 If the 3 order matrix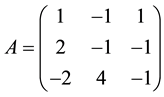
singular, solving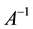
From Definition 2.1 we get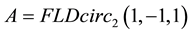

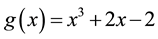
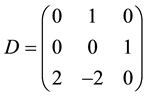
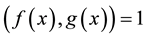
After a series of elementary row transformation of the following polynomial matrix, we obtain
So
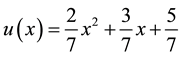
Therefore
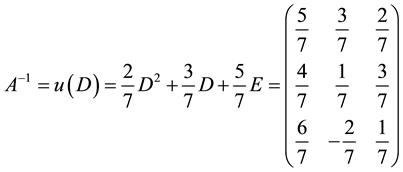
That is
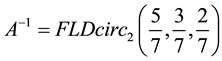
Example 5.2 If the 3 order matrix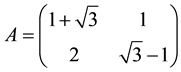
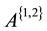
From Definition 2.1 we have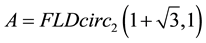
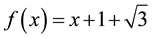
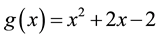

Then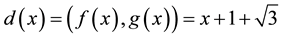
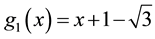
From Step 3, we get
Then
So
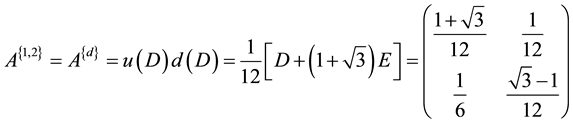
That is
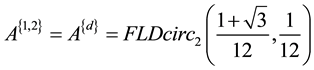
Acknowledgements
The authors are grateful to the anonymous referees for their review comments and suggestions that help to improve the original manuscript.
References
- Searle, S.R. (1979) On Inverting Circulant Matrices. Linear Algebra and Its Applications, 25, 77-89. http://dx.doi.org/10.1016/0024-3795(79)90007-7
- Tolomei, P.B. and Torres, L.M. (2013) On the First Chvátal Closure of the Set Covering Polyhedron Related to Circulant Matrices. Electronic Notes in Discrete Mathematics, 44, 377-383. http://dx.doi.org/10.1016/j.endm.2013.10.059
- Bozkurt, D. and Tam, T.-Y. (2012) Determinants and Inverses of Circulant Matrices with Jacobsthal and Jacobsthal-Lucas Numbers. Applied Mathematics and Computation, 219, 544-551. http://dx.doi.org/10.1016/j.amc.2012.06.039
- Wu, A.-G., Zeng, X.L., Duan, G.-R. and Wu, W.-J. (2010) Iterative Solutions to the Extended Sylvester-Conjugate Matrix Equations. Applied Mathematics and Computation, 217, 130-142. http://dx.doi.org/10.1016/j.amc.2010.05.029
- Shen, S.Q. and Cen, J.M. (2010) On the Bounds for the Norms of r-Circulant Matrices with the Fibonacci and Lucas Numbers. Applied Mathematics and Computation, 216, 2891-2897. http://dx.doi.org/10.1016/j.amc.2010.03.140
- Zellini, P. (1979) On Some Properties of Circulant Matrices. Linear Algebra and Its Applications, 26, 31-43. http://dx.doi.org/10.1016/0024-3795(79)90170-8
- Davis, P.J. (1994) Circulant Matrices. 2nd Edition, Chelsea Publishing, New York.
- Xu, Q.-Z., Li, H.-Q. and Jiang, Z.-L. (2005) An Algorithm for Finding the Minimal Polynomial of Fls r-Circulant Matrix. Journal of Mathematics (PRC), 25, 599-604.
- He, C.Y. and Wang, X.Y. (2014) The Discriminance for a Special Class of Circulant Matrices and Their Diagonalization. Applied Mathematics and Computation, 238, 7-12. http://dx.doi.org/10.1016/j.amc.2014.04.007
- Zhou, J.W. and Jiang, Z.L. (2014) The Spectral Norms of g-Circulant Matrices with Classical Fibonacci and Lucas Numbers Entries. Applied Mathematics and Computation, 233, 582-587. http://dx.doi.org/10.1016/j.amc.2014.02.020
- Bell, C.L. (1981) Generalized Inverses of Circulant and Generalized Circulant Matrices. Linear Algebra and Its Applications, 39, 133-142. http://dx.doi.org/10.1016/0024-3795(81)90297-4
- Jiang, Z.-J. and Xu, Z.-B. (2005) Efficient Algorithm for Finding the Inverse and the Group Inverse of FLSr-Circulant Matrix. Journal of Applied Mathematics and Computing, 18, 45-57. http://dx.doi.org/10.1007/BF02936555