Received 10 October 2014; revised 10 November 2014; accepted 8 December 2014

ABSTRACT

In this paper, it is proved that every nonlinear Jordan triple derivation on triangular algebra is an additive derivation.

Keywords:

Nonlinear Jordan Triple Derivations, Triangular Algebras, Derivation

1. Introduction

Let 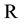be a commutative ring with identity and 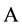be an 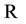-algebra. A linear map 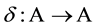is called a derivation if 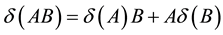for all 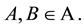Additive (linear) derivations are very important maps both in theory and applications, and were studied intensively. More generally, we say that 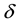is a Jordan

triple derivation if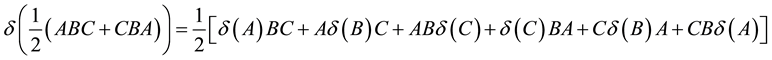

for all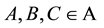. If the linearity in the definition is not required, the corresponding map is said to be a nonlinear Jordan triple derivation. It should be remarked that there are several definitions of linear Jordan derivations and all of them are equivalent as long as the algebra 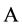is 2-torsion free. We refer the reader to [1] for more details and related topics. But one can ask whether the equivalence is also true on the condition of nonlinear, and we are still unable to answer this question.

The structures of derivations, Jordan derivations and Jordan triple derivations were systematically studied. Herstein [2] proved that any Jordan derivation from a 2-torsion free prime ring into itself is a derivation, and the famous result of Brešar ( [1] , Theorem 4.3) states that every Jordan triple derivation from a 2-torsion free semi- prime ring into itself is a derivation. For other results, see [3] - [9] and the references therein.

Let 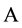and 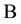be two unital algebras over a commutative ring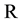, and let 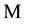be a unital 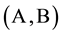-bi- module, which is faithful as a left 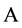-bimodule, that is, for and a right -bimodule,

that is, for. Recall the algebra

under the usual matrix addition and formal matrix multiplication is called a triangular algebra [10] . Recently, Zhang [11] characterized that any Jordan derivation on a triangular algebra is a derivation. In this paper we present result corresponding to [11] (Theorem 2.1) for non-linear Jordan triple derivations (there is no linear or additive assumption) on an important algebra: triangular algebra.

As a notational convenience, we will adopt the traditional representations. Let us write, and for the identity matrix of the triangular algebra.

2. The Main Results

In this note, our main result is the following theorem.

Theorem 2.1. Let and be unital algebras over a 2-torsion free commutative ring, and be a unital -bimodule, which is faithful as a left -bimodule and a right -bimodule. Let be the triangular algebra; if is a nonlinear Jordan triple derivation on, is an additive derivation.

Lemma 2.1. If is a nonlinear Jordan triple derivation on an upper triangular algebra generated by with.

Proof. It follows from the fact that, which implies that Thus we have from the fact that that where

Now define for each Clearly, is also a nonlinear Jordan triple deri- vation from into itself. It follows from Lemma 2.1 that

Lemma 2.2.

Proof. Clearly,

Lemma 2.3.

Proof. Firstly, we prove that It is clear that

which implies that

Let Since

we get

Let and thus

Similarly, one can check that

Lemma 2.4.

Proof. For any it follows from Lemma 2.3 that

This implies that Since

is a faithful left -module, we have that

It follows from, we have Similarly, we can get that

Lemma 2.5. For any, we have

(1), (2),

(3), (4).

Proof. (1) For any it follows from Lemma 2.3 and 2.4; we have

(2) is proved similarly.

(3) For any by Lemma 2.5 (1), we get that

(1)

On the other hand,

This and Equation (1) imply that

Since is a faithful left -module and, we get that is

Similarly, (4) is true for all.

Lemma 2.6. and.

Proof. Let, it follows from Lemma 2.2 and 2.4, we have that

that is,

For any it follows from Lemma 2.5 (1), we have

(2)

On the other hand,

This and Equation (2) imply that Since is a faithful left -mo-

dule; hence

Similarly, let, for any then

On the other hand,

Therefore, we get that is

So

Therefor combining Lemma 2.3, we have

that is,

.

Similarly, (2) is true for all.

Lemma 2.7.

Proof. For any,

Thus,

Lemma 2.8. For any we have

Proof. For any from Lemma 2.3 and 2.6, we have

Lemma 2.9. is additive on and respectively.

Proof. For any by Lemma 2.5 (1), we have

(3)

on the other hand, from Lemma 2.5 (1) and 2.8, we get that

This and Equation (3) imply that

Since is a faithful left -module and, we have that that is

Similarly, we can also get the additivity of on

Lemma 2.10. is additivity.

Proof. For any write where Then Lemma 2.7-2.9 are all used in seeing the equation

Lemma 2.11. for all.

Proof. For any let where Now we have that by Lemma 2.5 (1)-(4), Lemma 2.7 and 2.8

On the other hand, it follows from Lemma 2.3, 2.7; we get that

It is clear that for all

Proof of Theorem 2.1. From the above lemmas, we have proved that is an additive derivation on. Since for each, by a simple calculation, we see that is also an additive derivation. The proof is completed.

Acknowledgements

The author would like to thank the editors and the referees for their valuable advice and kind helps.

References