Computational Molecular Bioscience
Vol.2 No.3(2012), Article ID:22492,9 pages DOI:10.4236/cmb.2012.23008
Modeling Structures and Spectra of Fluorescent Proteins in the Coordinate-Locking Cluster Approach: Application to the Photoswitchable Protein asFP595
1Advanced Biomedical Computing Center, Information Systems Program, SAIC-Frederick Inc., Frederick National Laboratory for Cancer Research, Frederick, USA
2Chemistry Department, M.V. Lomonosov Moscow State University, Moscow, Russian Federation
3N.M. Emanuel Institute of Biochemical Physics, Russian Academy of Sciences, Moscow, Russian Federation
Email: *topoli@mail.nih.gov
Received July 19, 2012; revised August 20, 2012; accepted August 28, 2012
Keywords: Chromophore-Containing Pockets; Coordinate-Locking Scheme; ZINDO; Photoswitchable Fluorescent Proteins; asFP595
ABSTRACT
An interest in the fluorescent protein asFP595 is due to unexplained puzzles in its photophysical behavior. We report the results of calculations of structures, absorption, and emission bands in asFP595 by considering model molecular clusters in the coordinate-locking scheme. Both trans and cis conformations of the anionic chromophore are considered. Equilibrium geometry coordinates on the ground potential energy surface were optimized in the density functional theory approaches by considering both largeand reduced-size clusters. The cluster size was reduced to locate positions of the minimum energy points on the excited-state potential surface by using the configuration interaction singles approach. Vertical excitation energies and oscillator strengths were computed by using the ZINDO method. We show that consideration of large clusters mimicking the protein-containing pocket is an essential issue to calculate positions of absorption and emission bands with the accuracy compatible to experiments.
1. Introduction
Knowledge of a detailed picture of the events occurring in the chromophore-containing domains of photosensing proteins at atomic resolution is important for a rational design of novel fluorescent proteins with improved properties. Modern molecular modeling tools including quantum chemistry methods are of considerable value in this research contributing considerably to this field [1-30]. When performing such simulations, questions of accuracy and speed of calculations are the important issues for quick prediction of spectral bands in mutated proteins, which is a typical request from experimentalists. At one extreme, elaborate approaches based on quantum mechanics-molecular mechanics (QM/MM) optimization of geometry coordinates in the chromophore-containing domains, followed by expensive ab initio calculations of excitation energies (e.g., by using versions of configuretion interaction (CI) and perturbation theory-based methods, CASPT2 and MCQDPT2), are described in the literature [4,10,13,14,20,22,27,30-32]. The significance of these approaches is highly recognized; however, time and computational resources are quite demanding for these approaches to be routinely applied to a series of calculations. At another extreme, multiple attempts to apply inexpensive TD DFT [33] and ZINDO [34] methods to evaluate vertical excitation energies for model systems composed of the chromophore and small fractions of the environmental molecular groups of protein have often resulted in uncertain conclusions. Since the first calculations for the DsRed protein [1], in which the authors demonstrated that ZINDO provided reasonable estimates for absorption bands, and TD DFT was highly inferior to ZINDO, the progress along this line has been fairly slow.
In this work we demonstrate that higher accuracy in ZINDO-based calculations may be achieved by considering fairly large molecular clusters mimicking chromophore-containing domains of proteins with a careful optimization of geometry coordinates by using the coordinate-locking scheme. The latter is widely applied in a related field, i.e., in simulations of enzymatic reactions [35]. In this approach, a model molecular system has been constructed, as taken from the protein matrix, and certain atomic coordinates at the periphery of the model are fixed, as in the reference moieties, such as crystal or other reliable structures, upon optimization of geometry coordinates. For the systems with carefully optimized geometry parameters, ZINDO has been found to be very efficient in computing bands in optical spectra. As shown in our previous applications for several classes of fluorescent proteins [19,21,24], such a strategy in fact leads to accurate results that are comparable to the experimenttal values. In this work we show that an elaborate selection of model clusters in the coordinate-locking scheme and an application of fairly inexpensive quantum chemistry methods allow us to calculate bands both in the absorption and in the emission spectra of proteins. Such clusters can be designed when starting from the coordinates of heavy atoms of relevant structures deposited to the Protein Data Bank (PDB). After the addition of hydrogen atoms, a model system can be equilibrated by using classical molecular dynamics (MD) simulations, followed by geometry optimization using the QM/MM technique with a relatively small quantum subsystem. These preliminary steps allow one to achieve general relaxation of atomic coordinates in the chromophore-conining domain. The final treatment of a large cluster alows one to describe interaction of the chromophore with an extended environment at the exclusive quantum level and to eliminate ambiguous effects of the QM/MM boundary.
Colored protein asFP595, a natural protein from Anemonia sulcata, and its Ala143Gly variant called kindling fluorescent protein (KFP) [36-44], are important members of the GFP family. Upon light illumination at low intensities, asFP595 and KFP are weakly fluorescent with a very low quantum yield. However, high-intensity irradiation with green light leads to a nonlinear dependence of the fluorescence intensity on excitation energy and to a drastic increase of the quantum yield. Such kindling is reversible, since upon blue light illumination or in the dark, the proteins return to the initial nonfluorescent state. The reversible photoswitching is highly attractive for developments in optical microscopy much below the diffraction limit. Also, KFP is considered a convenient acceptor partner in the Förster resonance energy transfer (FRET) pair with brightly fluorescent red protein TagRFP. Employing FRET between these two proteins connected by an appropriate peptide linker opens new perspectives for monitoring biological and physiological mechanisms and for creating novel diagnostic tools [45, 46].
Beyond promising practical applications, studies of asFP595 are of considerable importance, due to challenging puzzles in its photophysical behavior. The reasons for increased red fluorescence of the initially non-fluorescent species upon intense green light illumination are not yet fully understood. The current working hypothesis relates the photoswitching phenomenon in asFP595 and KFP to the light-induced tran-cis isomerization of the chromophore inside the protein matrix. In spite of certain evidence provided in favor of this viewpoint by the crystal structures of asFP595 and KFP [39-41], especially in the work of Andresen et al. [40], no direct proof has been found to demonstrate such a trans-cis isomerization route in the protein environment. The MD-created movie in ref. [40] for the trans-cis transformations may be considered as a nice visualization but not as a strong argument. Even more intriguing is a recent demonstration of protein kindling in the experiments in solutions by varying pH [25]. Namely, it has been demonstrated that at physiological pH the KFP variant is still a weakly fluorescent species; however, the intensity of fluorescence is considerably increasing upon shifting pH to alkaline values. Tentative mechanisms of pH-induced kindling were discussed in ref. [25] which did not exclude increase of population of proteins with the cis-isomer of the chromophore.
Apparently, there is a strong need to provide a detailed picture of the photo-induced processes in asFP595 and KFP at atomic resolution, starting from structural and spectral properties. Reliable theoretical estimates for the emission spectrum are still unknown, and no firm assignment of the observed peak at 595 nm to a specific chromophore isomer has yet been made. We show that the computed band position both in absorption and in emission correlate well with experimentally observed band maxima what provides a solid support to the so far tentative assignments of the spectral bands.
2. Models and Computational Protocol
The model clusters mimicking the chromophore containing pocket were prepared as follows. The crystal structure PDB 2A50 [40] of the wild-type asFP595 with the trans-anionic chromophore served as an initial source of coordinates of heavy atoms. After addition of hydrogen atoms assuming a generally accepted protonation scheme for polar amino acid residues Arg, Lys (positively charged), and Asp, Glu (negatively charged), the geometry coordinates were optimized by using the flexible effective fragment potential QM/MM method [47,48]. The QM subsystem described at the restricted Hartree-Fock method with the 6-31G basis set level was composed of Chro, Arg92, Ser158, His197, and Glu215. The MM subsystem was described with the AMBER force field parameters. This level of theoretical approach is suitable for preliminary geometry optimization on the ground state potential surface, but apparently is not sufficient for quantitative predictions, first of all, because of small basis set and absence of correlation contributions. On the other hand, we needed QM/MM minimization as a preliminary step before cluster calculations in order to prepare a better relaxed all-atom model initiated by the coordinates of heavy atoms only in the crystal structure. We examined the superposition of the QM/MM optimized and crystal (PDB 2A50) structures (Figure 1) and found that theoretical coordinates of backbone atoms were well reproduced in simulations. QM/MM calculations were performed by using the modified version of the GAMESS(US) package [49].
Next, we manually selected 20 amino acid residues completely surrounding the chromophore, as well as nine crystallography-resolved water molecules to form a model cluster, as shown in Figure 2. By such selection, first of all, we intended to form a closed shell around the chromophore, and secondly, to maintain the hydrogen
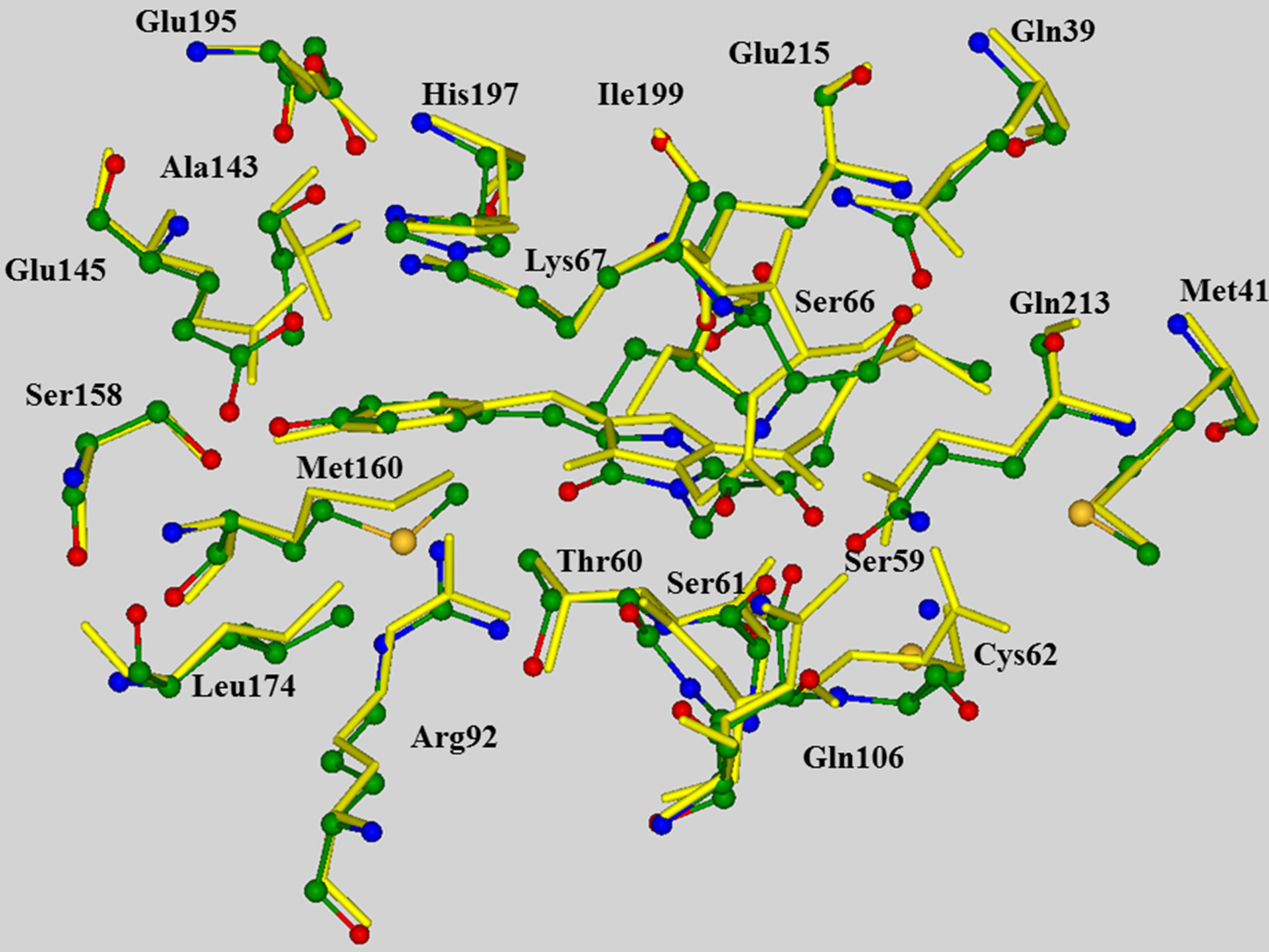
Figure 1. Superposition of the QM/MM optimized chromophore-containing domain of asFP595 (multicolored balls and sticks for heavy atoms) and the corresponding fragment of the crystal structure PDB 2A50 (yellow sticks), showing that the computed positions of peripheral backbone atoms correlate well with the crystal sites. In all figures, carbon atoms are shown in green, oxygen in red, nitrogen in blue.
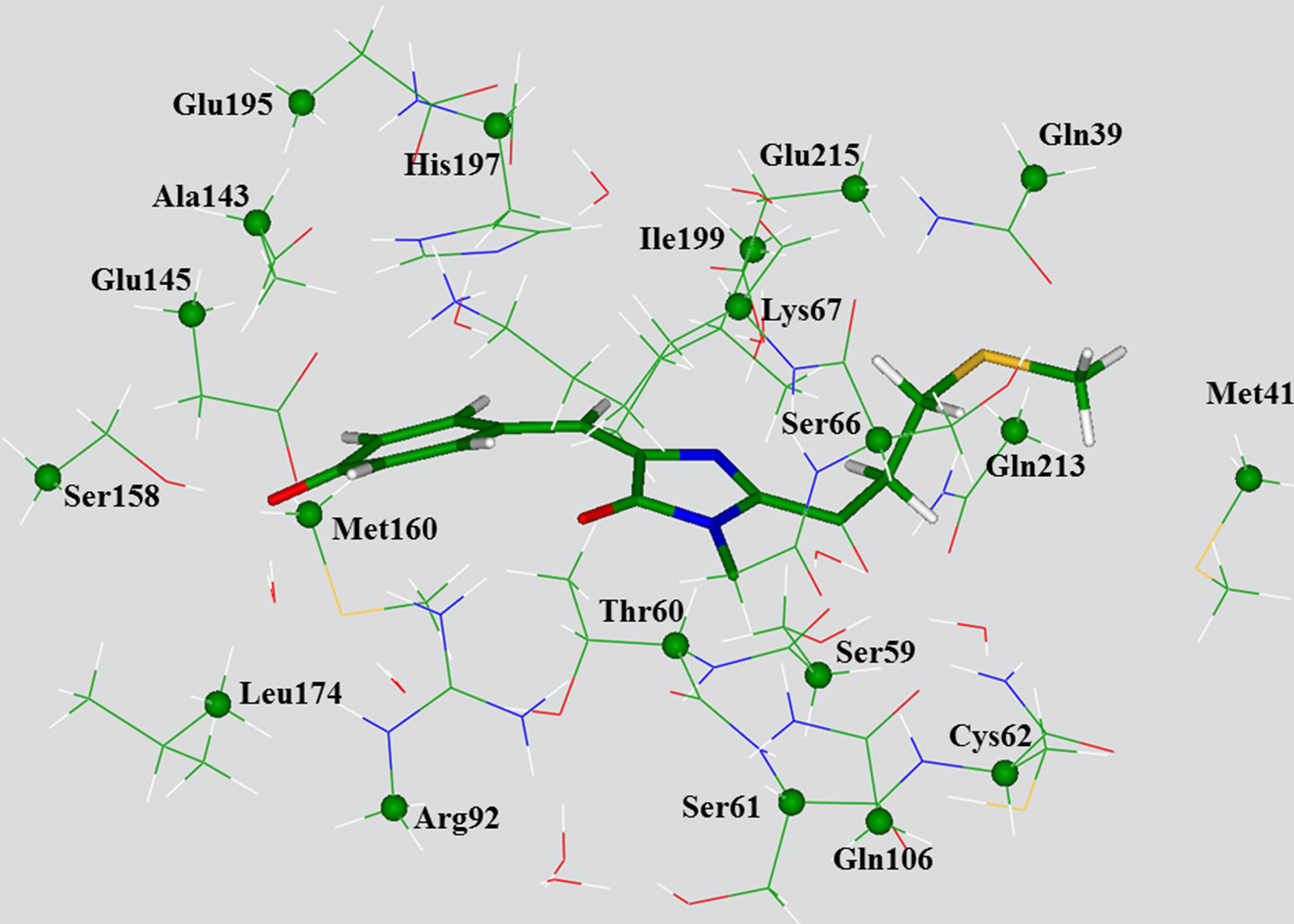
Figure 2. View of the large model cluster with the transanionic chromophore used for calculations of absorption bands. The chromophore molecule is shown by sticks. The carbon atoms whose coordinates have been kept frozen in optimization of ground state geometry parameters as in QMM/MM (crystal) are specified by balls.
bon network around the chromophore. In total, the system included 308 atoms for the case of anionic chromophore. In Figure 1, the selected carbon atoms whose coordinates were kept frozen in subsequent geometry optimizations were indicated by colored balls. We used the B3LYP/6-31G(d) approximation of the density functional theory (DFT) methodology to find equilibrium coordinates for the ground state. These coordinates were used to compute vertical excitation energies by using the ZINDO method. Model clusters with the chromophore in the cis form were constructed manually, and their coordinates were re-optimized in the same DFT approximation.
As we see below, the position of absorption bands of the protein is well reproduced for the clusters of such size. However, in order to make a feasible location of energy minima on the excited state potential surface by using the configuration interaction with singles (CIS) method with a subsequent estimation of the emission bands, we had to reduce the number of atoms included in calculations. Reduction of the cluster size was performed manually in such a way that the hydrogen bond network spanning the chromophore and the immediate residues should be substantially conserved with respect to the large clusters. Finally, the 214-atomic cluster (for the case of the trans-anionic chromophore) was designed. Figure 3 illustrates the corresponding model system and shows explicitly which of the peripheral carbon atoms coordinates were kept frozen as in the large cluster (Figure 1) upon optimization of internal coordinates, both in the ground state by using B3LYP/6-31G(d) and in the first excited singlet state by using CIS/6-31G(d).
DFT, CIS and ZINDO calculations were performed by
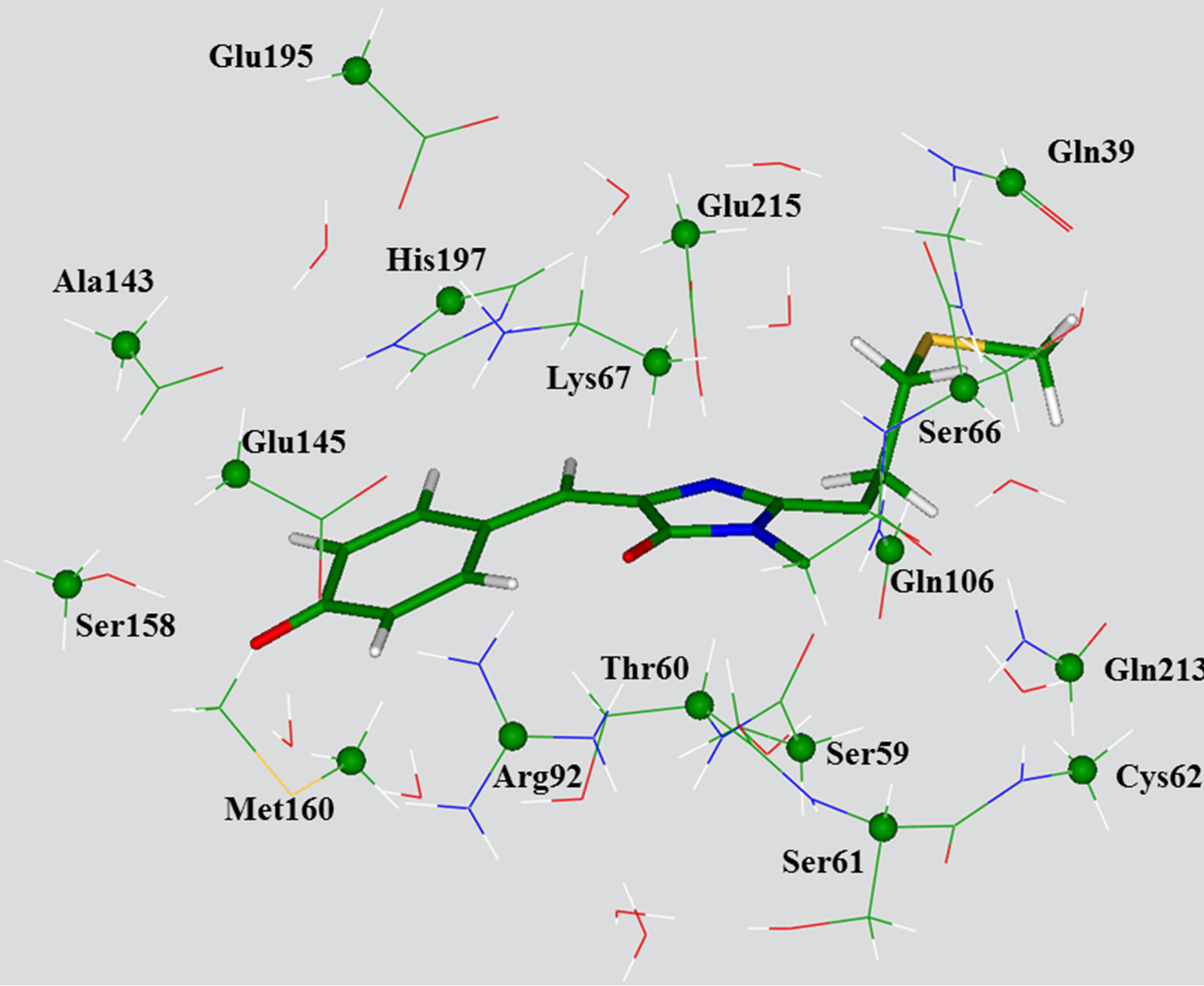
Figure 3. View of the reduced model cluster with the transanionic chromophore used for calculations of absorption and emission bands. The chromophore molecule is shown by sticks. The carbon atoms whose coordinates have been kept frozen in optimization of ground state geometry parameters, as in the large cluster, are specified by balls.
using Gaussian03 [50].
3. Results
Firstly, we briefly mention the results of calculations performed for the anionic gas-phase chromophore species (2-acetyl-4-(p-hydroxybenzylidene)-1-methyl-5-imidazolone) shown in Figure 4. Equilibrium geometry coordinates of these molecules were obtained in the B3LYP/6- 31 + G(d,p) approximation by using slightly more extended basis sets than those (6-31G(d)) used for the molecular clusters.
The ZINDO results for the absorption band maxima of the isolated chromophores are 556 nm (or 2.23 eV) for the trans isomer and 569 nm (or 2.18 eV) for the cis isomer. Previous calculations of the vertical excitation energies for the asFP595 chromophore in vacuo [5,6,13-15] in fact show a diversity of results, the most reliable of which [13,14] systematically predict the excitation energy of the cis isomer somewhat lower (about 0.09 - 0.15 eV) than that of the trans isomer. In this respect, the present ZINDO//DFT results are consistent with the higherlevel approaches.
Emission band maxima of the isolated chromophores were evaluated as the vertical energy differences between S0 and S1 states at the geometry coordinates optimized in the first excited state S1 by using the CIS/6-31+G(d,p) procedure. We obtained 565 nm (2.19 eV) for the trans isomer and 578 nm (2.14 eV) for the cis isomer. These ZINDO results illustrate a trend showing that the cis form of the chromophore that the CIS vertical energy differences between two electronic states were strongly overestimated; however, ZINDO at the CIS optimized geometry parameters performed well.
Figure 5 illustrates arrangements of the key residues around the chromophore in the trans-configuration (toppanel) and in the cis-configuration (bottom panel), ac
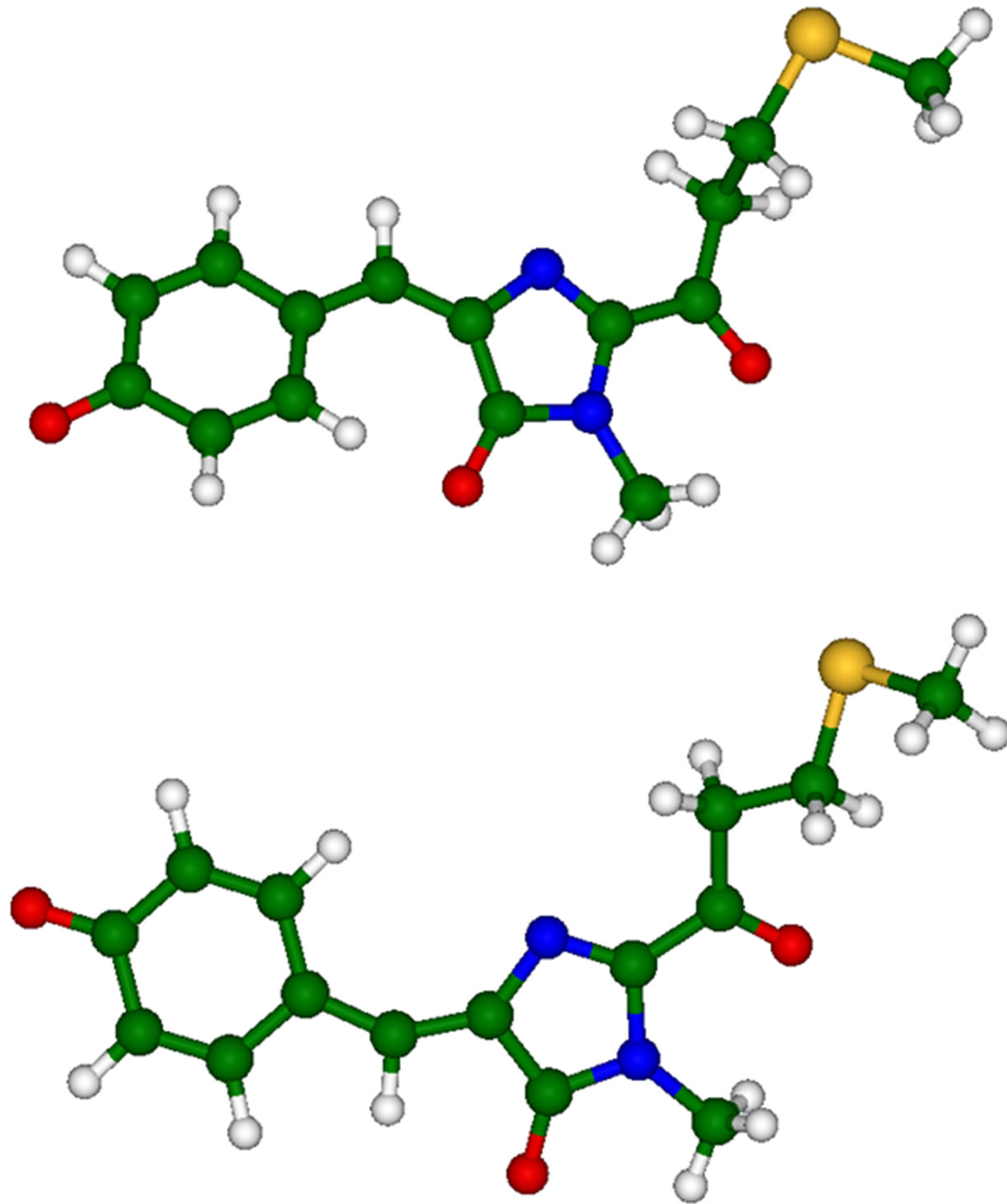
Figure 4. Chromophore molecules of asFP595 in trans (top panel) and cis (bottom panel) anionic forms.
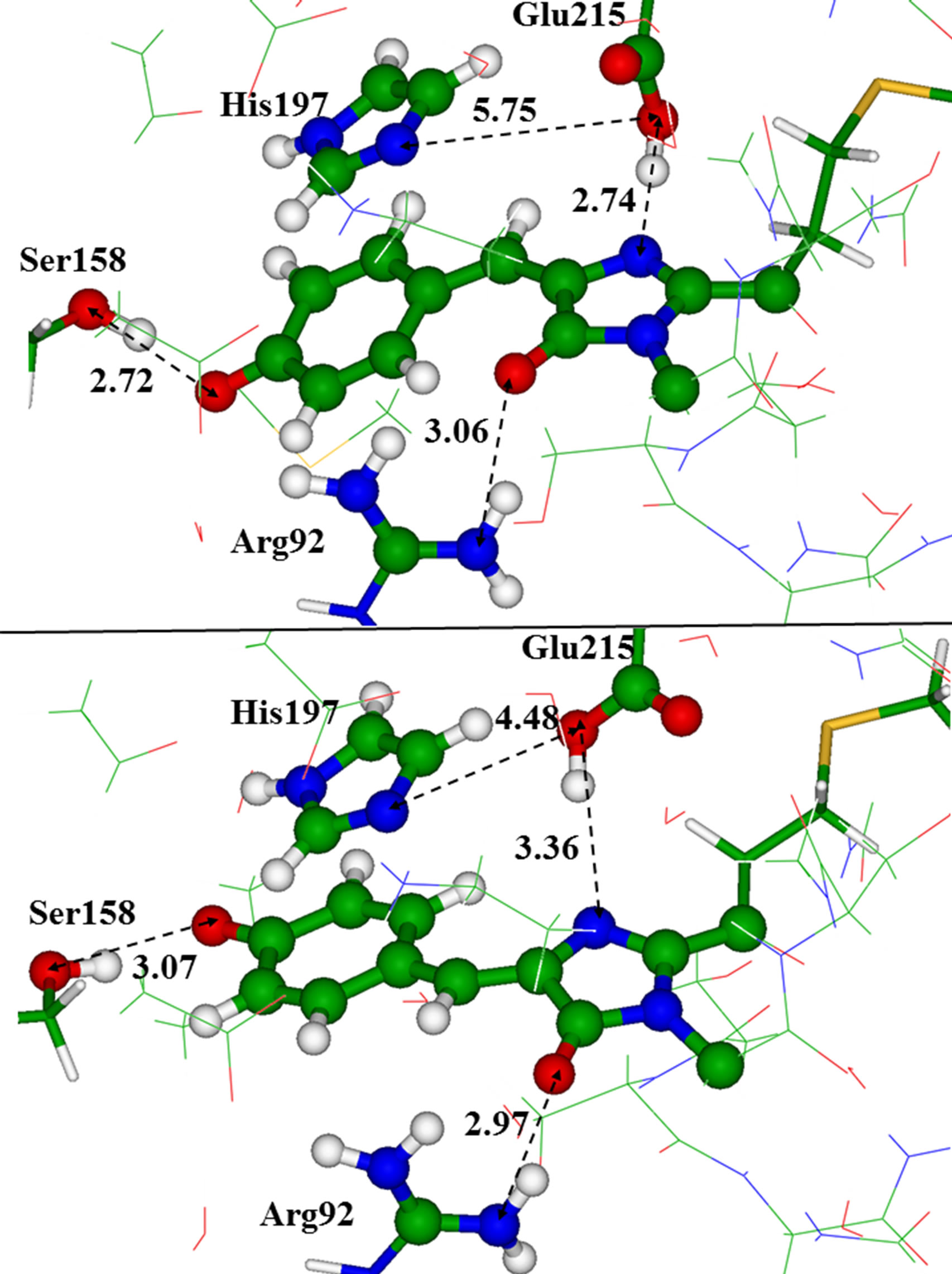
Figure 5. The chromophore in the trans (top panel) and in the cis (bottom panel) conformations inside the model clusters. Distances are given in angstroms.
cording to the results obtained for the reduced clusters. Apparently, the most noticeable difference between structures with these two chromophore conformers is in orientation of the Glu215 side chain with respect to the chromophore and to the His197 side chain. For the latter, we assume the neutral (deprotonated) state.
The most intense transitions in the absorption and emission spectra occur between S0 and S1 states associated with the predominant π - π* electron distributions over the chromophore. We collected in Table 1" target="_self"> Table 1 the results of calculations of the wavelengths, oscillator strengths and corresponding energy differences for the vertical transitions in the model clusters. The second and third rows contain the values obtained in the ZINDO//DFT approximation. An assignment of the observed band in the absorption spectrum at 568 nm to the protein conformation with the trans-anionic chromophore is assumed in experimental studies [37,38,40,42,43]. The computationally obtained value at 572 nm perfectly matches such an assignment,although our result for the system with the cis isomer (570 nm) also does not contradict observations.
When comparing the results obtained for large clusters and reduced clusters, we noted that reduction of the model system worsens an agreement between computed and experimental values if the ZINDO//DFT approach is employed.

Table 1. Calculated wavelengths, oscillator strengths (values in the parentheses) and energy differences for the vertical transitions corresponding to the absorption and emission bands in asFP595.
In the last row of Table 1, we presented the suggested interpolations for the cluster size, assuming that the errors in computing vertical excitation energies due to reduction of a model cluster do not change considerably along potential surfaces. Comparing data in the second row, we deduced that such errors due to reduction of the cluster for the absorption bands are 0.07 eV (2.23 - 2.16) for systems with the trans isomer and 0.09 eV (2.26 - 2.17) for the cis isomer. If such corrections are applied for the emission bands, we arrived at the values shown in the last row of Table 1. The simulated wavelength in the emission spectrum of a large cluster modeling the protein with the cis anionic chromophore, 599 nm, perfectly matches the observed band at 595 nm. Therefore, this work reports data for both known bands in optical spectra of asFP595 (568 nm in absorption and 595 nm in emission) calculated almost precisely, thus providing a firm assignment of these bands to specific protein conformations: trans anionic chromophore for 568 nm and cis anionic chromophore for 595 nm.
We also examined whether certain variations in the model clusters could affect computed band positions in absorption spectra. Each variation assumed re-optimization of geometry coordinates in the coordinate-locking scheme, followed by ZINDO calculations. There are several versions of the asFP595 protein crystallographic structures available in the protein data bank. For the purposes mentioned above we used crystal structure PDB 2A52 [40] characterized by cis anionic chromophore and mutation of Ser158 by Val. The last mutation did not cause any significant changes in the excitation energies for the S0 - S1 transition. The extensively debated issue for this protein is the protonation state of the His197 side chain. We found that its protonation worsened an agreement between theory and experiment for absorption bands. The value for the absorption band for the cluster with the protonated His197 (557 nm) was shifted by 12 nm to the red side with respect to the value obtained for the cluster with neutral His197 (569 nm). Moreover, the position of the imidazole ring of His197 almost coplanar to the phenolic ring of the chromophore, as observed in the crystal structure, is much better reproduced in cluster calculations with the neutral His197. All these considerations allow us to conclude that His197 in the asFP595 should be in the neutral form.
As illustrated in Figure 5 there is more space between Glu215 and the chromophore in the domain with the cis anionic chromophore due to a week hydrogen bond between Glu215 and the chromophore. This space may be occupied by single water molecule close to Glu215. We found two conformations of the large model cluster, corresponding to two minima on the ground-state potential energy surface. These minimum energy structures differed by the hydrogen bond patterns; namely, the side chain of Glu215 could form a hydrogen bond with the chromophore (as shown in Figure 5), or that with a water molecule capable to fit the cavity. Absence of a hydrogen bond between Glu215 and the chromophore due to direct interaction of Glu215 with the water molecule led to a small red shift in the absorption band by 5 nm.
4. Discussion
It is important to compare the results described in this work with previous computational data aiming to simulate absorption bands for the same protein. Beyond several contributions in which only the chromophore molecule in the gas-phase was simulated, two groups reported vertical excitation energies from the ground state for the chromophore-containing domains of asFP595 or KFP. Grigorenko et al. [8,9] performed QM/MM optimization of geometry parameters of the model system composed of more than 2,000 atoms when starting from the coordinates of heavy atoms from the structure PDBID: 1XMZ [39] of KFP. The entire chromophore unit and the side chains of the neighboring His197 (in the protonated state), Glu215, and Arg92 amino acids were assigned to the 50- atomic subsystem comprising the QM part treated at the RHF/6-31G(d) level. The MM subsystem was represented by a set of small effective fragments [47,48]. Interactions between the fragments were modeled by using AMBER force field parameters. Both conformations of the protein with the trans and cis anionic chromophore were optimized in QM/MM calculations. Vertical excitation energies were computed for the quantum subsystem (chromophore, His197, and Glu215) by using TD DFT in the B3LYP/6-31 + G(d) approximation. In another paperSchäfer et al. [11] modeled absorption bands in the asFP595 protein by using the following computational protocol. Geometry optimization of the ground state geometry parameters was performed when starting from the crystal structure PDB 2A50 [40]. The model systems were relaxed by using classical molecular dynamics simulations and brief QM/MM (HF/3-21G(d), ONIOM) minimizations by assigning only the chromophore to the QM subsystem; then the ZINDO and TD DFT methods were used to estimate the vertical excitation energies. In these calculations, the chromophore and the side chains of the nearby residues Lys67, Arg92, Glu145, Ser158, His197 (in the protonated state), and Glu215 were included in quantum calculations. It was concluded that TD DFT values were not reliable, although the values were qualitatively consistent with ZINDO results.
We collected the results of all three computational papers for the absorption bands in asFP595/KFP in Table 2 which should be compared to the experimental absorption band maximum in asFP595 at 568 nm and in KFP (the Ala143Gly mutant of asFP595) at 575 nm [37]. Apparently, differences in the structures (Ala stands at the 143 position in asFP595, but Gly in KFP) do not seriously affect the position of the absorption band. According to our estimates as mentioned above, protonation of the His 197 side chain, as assumed in previous research [8,9,11], also does not affect the strongly computed position of the absorption band, compared to the unprotonated status of His197 (as used in this work). Therefore, it is reasonable to assume that the results of all three papers presented in Table 2 refer to the similar model system.
These results illustrate the tendencies noted in the literature: ZINDO performs better than TD DFT for systems of comparable size (cf. line 2 and lines 3,4). Comparison of two bottom lines show that the more extended quantum system is selected for ZINDO calculations, the results are better: the size of the quantum part in ref. [11] was considerably smaller than in the present work. Discrepancies of 0.2 - 0.3 eV (or about 50 nm) between experimental and computed absorption bands are typical when ZINDO is used for small quantum model systems. In this respect, we mention the recent paper devoted to studies of the mKate fluorescent protein [51], in which the chromophore and a couple of the nearest residues were included in ZINDO calculations, following QM/MM optimization of the ground state geometry coordinates; the errors in absorption band maxima were of exactly the same order (≈60 nm).

Table 2. Calculated wavelengths and energy differences for the vertical transitions corresponding to the absorption bands in asFP595/KFP.
We believe that in our work we have found an adequate size of model clusters that allowed us to approach very closely to the experimental data. We mention that the same computational strategy, which is using large molecular clusters in the coordinate-locking scheme, can be applied to simulate structure and spectra of asFP595 with the neutral form of the chromophore. These calculations, performed to provide interpretation of another series of experiments with this protein, followed the same computational protocol, i.e., selection of the appropriate protein structure, its refinement in molecular dynamics and preliminary QM/MM simulations, creation of a large molecular cluster, DFT optimization of geometry parameters in the coordinate-locking scheme, followed by ZINDO calculations. These results are published elsewhere (ref. [52]); however, for the goals of this work, it is worth reporting that an agreement between the experimental absorption band maximum (445 nm) [37] and computed excitation wavelength (437 nm) is also excellent. However, when acknowledging success of the present studies we have to admit that a careful examination of results are required at every ZINDO application since the reasons for such accuracy are not perfectly clear.
For the first time, the computational approach reports the emission band in asFP595 with an accuracy comparable to experimental studies. We can firmly assign fluorescence in asFP595 to the protein conformation with the anionic chromophore. Consideration of zwitterionic structures sometimes assumed in asFP595/KFP photophysics [11] should be dismissed. Although the values 584 nm for emission from the trans chromophore and 599 nm for emission from the cis chromophore (see Table 1) are not firmly distinguishable, the latter model system (with the cis anionic chromophore) is closer to the experimental band at 595 nm. Therefore, we obtained some indication that the protein conformation with the cis anionic chromophore is responsible for fluorescence; thus, the working hypothesis on the trans-cis chromophore isomerization gains some support in this work.
5. Conclusion
We performed calculations of the structures and optical bands in the photoswitchable fluorescent protein asFP595 in its most important conformations. The use of large molecular clusters mimicking the chromophore containing domain, careful DFT-based and CIS-based geometry optimization within the coordinate-locking scheme, as well as the application of ZINDO technique, which is particularly suitable for organic chromophores, are responsible for the accuracy compatible to experimental values when computing optical spectra. Correspondence of the computed band position in absorption for the conformation with the trans-anionic chromophore at 572 nm and in emission for the conformation with the cis-anionic chromophore at 599 nm with the experimentally observed band maxima (568 nm and 595 nm, respectively) provides a solid support to the so far tentative assignments of the spectral bands and to involvement of the trans-cis chromophore isomerization in this protein upon kindling.
6. Acknowledgements
We thank the staff and administration of the Advanced Biomedical Computing Center for their support of this project. We thank Dr. Brian Luke for very helpful comments. This project has been funded in whole or in part with federal funds from the National Cancer Institute, National Institutes of Health, under contract number HHSN261200800001E. The content of this publication does not necessarily reflect the views or policies of the Department of Health and Human Services, nor does mention of trade names, commercial products, or organization imply endorsement by the US government. This work is partly supported by the Russian Foundation for Basic Research (project 10-03-00085) and the Program of Molecular and Cell Biology from the Russian Academy of Sciences.
REFERENCES
- L. A. Gross, G. S. Baird, R. C. Hoffman, K. K. Baldridge and R. Y. Tsien, “The Structure of the Chromophore within DsRed, a Red Fluorescent Protein from Coral,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 97, No. 22, 2000, pp. 11990-11995. doi:10.1073/pnas.97.22.11990
- M. Zimmer, “Green Fluorescent Protein (GFP): Applications, Structure, and Related Photophysical Behavior,” Chemical Reviews, Vol. 102, No. 3, 2002, pp. 759-782. doi:10.1021/cr010142r
- T. Laino, R. Nifosì and V. Tozzini, “Relationship between Structure and Optical Properties in Green Fluorescent Proteins: A Quantum Mechanical Study of the Chromophore Environment,” Chemical Physics, Vol. 298, No. 1-3, 2004, pp. 17-28. doi:10.1016/j.chemphys.2003.10.040
- A. Sinicropi, T. Andruniow, N. Ferre, R. Basosi and M. Olivucci, “Properties of the Emitting State of the Green Fluorescent Protein Resolved at the CASPT2//CASSCF/ CHARMM Level,” Journal of the American Chemical Society, Vol. 127, No. 33, 2005, pp. 11534-11535. doi:10.1021/ja045269n
- P. Amat, G. Granucci, F. Buda, M. Persico and V. Tozzini, “The Chromophore of asFP595: A Theoretical Study,” The Journal of Physical Chemistry B, Vol. 110, No. 18, 2006, pp. 9348-9353. doi:10.1021/jp057071a
- M. Sun, “Excited State Properties of the Chromophore of the asFP595 Chromoprotein: 2D and 3D Theoretical Analyses,” International Journal of Quantum Chemistry, Vol. 106, No. 4, 2006, pp. 1020-1026. doi:10.1002/qua.20815
- A. V. Nemukhin, I. A. Topol and S. K. Burt, “Electronic Excitations of the Chromophore from the Fluorescent Protein asFP595 in Solutions,” Journal of Chemical Theory and Computation, Vol. 2, No. 2, 2006, pp. 292-299. doi:10.1021/ct050243n
- B. Grigorenko, A. Savitsky, I. Topol, S. Burt and A. Nemukhin, “Ground-State Structures and Vertical Excitations for the Kindling Fluorescent Protein asFP595,” The Journal of Physical Chemistry B, Vol. 110, No. 37, 2006, pp. 18635-18640. doi:10.1021/jp060124j
- B. Grigorenko, A. Savitsky, I. Topol, S. Burt and A. Nemukhin, “Trans and Cis Chromophore Structures in the Kindling Fluorescent Protein asFP595,” Chemical Physics Letters, Vol. 424, No.1-3, 2006, pp.184-188.
- J.-Y. Hasegawa, K. Fujimoto, B. Swerts, T. Miyahara and H. Nakatsuji, “Excited States of GFP Chromophore and Active Site Studied by the SAC-CI Method: Effect of Protein—Environment and Mutations,” Journal of Computational Chemistry, Vol. 28, No. 15, 2007, pp. 2443- 2452. doi:10.1002/jcc.20667
- L. V. Schäfer, G. Groenhof, A. R. Klingen, G. M. Ullmann, M. Boggio-Pasqua, M. A. Robb and H. Grubmüller, “Photoswitching of the Fluorescent Protein asFP595: Mechanism, Proton Pathways, and Absorption Spectra,” Angewandte Chemie, Vol.119, No. 4, 2007, pp. 536-542.
- L. V. Schäfer, G. Groenhof, M. Boggio-Pasqua, M. A. Robb and H. Grubmüller, “Chromophore Protonation State Controls Photoswitching of the Fluoroprotein asFP595,” PLOS Computational Biology Vol. 4, No. 3, 2008, p. e1000034. doi:10.1371/journal.pcbi.1000034
- S. Olsen and S. C. Smith, “Bond Selection in the Photoisomerization Reaction of Anionic Green Fluorescent Protein and Kindling Fluorescent Protein Chromophore Models,” Journal of the American Chemical Society, Vol. 130, No. 27, 2008, pp. 8677-8689. doi:10.1021/ja078193e
- K. B. Bravaya, A. V. Bochenkova, A. A. Granovsky, A. P. Savitsky and A. V. Nemukhin, “Modeling Photoabsorption of the asFP595 Chromophore,” The Journal of Physical Chemistry A, Vol. 112, No. 37, 2008, pp. 8804-8810. doi:10.1021/jp804183w
- A. V. Nemukhin, I. A. Topol, B. L. Grigorenko, A. P. Savitsky and J. R. Collins, “Conformation Dependence of pKa’s of the Chromophores from the Purple asFP595 and Yellow zFP538 Fluorescent Proteins,” Journal of Molecular Structure: THEOCHEM, Vol. 863, No. 1-3, 2008, pp. 39-43. doi:10.1016/j.theochem.2008.05.014
- P. J. Tonge and S. R. Meech, “Excited State Dynamics in the Green Fluorescent Protein,” Journal of Photochemistry and Photobiology A Chemistry, Vol. 205, No. 1, 2009, pp. 1-11.
- A. M. Virshup, C. Punwong, T. V. Pogorelov, B. A. Lindquist, C. Ko and T. J. Martinez, “Photodynamics in Complex Environments: Ab Initio Multiple Spawning Quantum Mechanical/Molecular Mechanical Dynamics,” The Journal of Physical Chemistry B, Vol. 113, No. 11, 2009, pp. 3280-3291. doi:10.1021/jp8073464
- A. V. Nemukhin, B. L. Grigorenko and A. P. Savitsky, “Computer Modeling of the Structure and Spectra of Fluorescent Proteins,” Acta Naturae, Vol. 1, No. 2, 2009, pp. 33-43.
- I. A. Topol, J. Collins, I. Polyakov, B. L. Grigorenko and A. V. Nemukhin, “On Photoabsorption of the Neutral Form of the Green Fluorescent Protein Chromophore,” Biophysical Chemistry, Vol. 145, No. 1, 2009, pp. 1-6. doi:10.1016/j.bpc.2009.08.002
- C. Filippi, M. Zaccheddu and F. Buda, “Absorption Spectrum of the Green Fluorescent Protein Chromophore: A Difficult Case for Ab Initio Methods?” Journal of Chemical Theory and Computation, Vol. 5, No. 8, 2009, pp. 2074- 2087. doi:10.1021/ct900227j
- I. Topol, J. Collins and A. Nemukhin, “Modeling Spectral Tuning in Monomeric Teal Fluorescent Protein mTFP1,” Biophysical Chemistry, Vol. 149, No. 3, 2010, pp. 78-82. doi:10.1016/j.bpc.2010.04.002
- S. Olsen, K. Lamothe and T. J. Martinez, “Protonic Gating of Excited-State Twisting and Charge Localization in GFP Chromophores: A Mechanistic Hypothesis for Reversible Photoswitching,” Journal of the American Chemical Society, Vol. 132, No. 4, 2010, pp. 1192-1193. doi:10.1021/ja907447k
- Y.-W. Hsiao, E. Sanchez-Garcia, M. Doerr and W. Thiel, “Quantum Refinement of Protein Structures: Implementation and Application to the Red Fluorescent Protein DsRed. M1,” The Journal of Physical Chemistry B, Vol. 114, No. 46, 2010, pp. 15413-15423. doi:10.1021/jp108095n
- I. Topol, J. Collins, A. Savitsky and A. Nemukhin, “Computational Strategy for Tuning Spectral Properties of Red Fluorescent Proteins,” Biophysical Chemistry, Vol. 158, No. 2-3, 2011, pp. 91-95. doi:10.1016/j.bpc.2011.05.016
- A. L. Rusanov, V. A. Mironov, A. S. Goryashenko, B. L. Grigorenko, A. V. Nemukhin and A. P. Savitsky, “Conformational Partitioning in pH-Induced Fluorescence of the Kindling Fluorescent Protein (KFP) ,” The Journal of Physical Chemistry B, Vol. 115, No. 29, 2011, pp. 9195- 9201. doi:10.1021/jp1094245
- I. Shelaev, V. Mironov, A. Rusanov, F. Gostev, A. Bochenkova, O. Sarkisov, A. Nemukhin and A. Savitsky, “The Origin of Radiationless Conversion of the Excited State in the Kindling Fluorescent Protein (KFP): Femtosecond Studies and Quantum Modeling,” Laser Physics Letters, Vol. 8, No. 6, 2011, pp. 469-474. doi:10.1002/lapl.201010145
- C. Filippi, F. Buda, L. Guidoni and A. Sinicropi, “Bathochromic Shift in Green Fluorescent Protein: A Puzzle for QM/MM Approaches,” Journal of Chemical Theory and Computation, Vol. 8, No. 1, 2011, pp. 112- 124. doi:10.1021/ct200704k
- G. Cui, Z. Lan and W. Thiel, “Intramolecular Hydrogen Bonding Plays a Crucial Role in the Photophysics and Photochemistry of the GFP Chromophore,” Journal of the American Chemical Society, Vol. 134, No. 3, 2012, pp. 1662-1672. doi:10.1021/ja208496s
- M. Wanko, P. García-Risueño and A. Rubio, “Excited States of the Green Fluorescent Protein Chromophore: Performance of Ab Initio and Semi-Empirical Methods,” Physica Status Solidi (b), Vol. 249, 2012, pp. 392-400. doi:10.1002/pssb.201100536
- K. B. Bravaya, B. L. Grigorenko, A. V. Nemukhin and A. I. Krylov, “Quantum Chemistry behind Bioimaging: Insights from Ab Initio Studies of Fluorescent Proteins and Their Chromophores,” Accounts of Chemical Research, Vol. 45, No. 2, 2012, pp. 265-275. doi:10.1021/ar2001556
- A. K. Das, J.-Y. Hasegawa, T. Miyahara, M. Ehara and H. Nakatsuji, “Electronic Excitations of the Green Fluorescent Protein Chromophore in Its Protonation States: SAC/ SAC-CI Study,” Journal of Computational Chemistry, Vol. 24, No. 12, 2003, pp. 1421-1431.
- K. B. Bravaya, A. V. Bochenkova, A. A. Granovsky and A. V. Nemukhin, “Modeling of the Structure and ElecTronic Spectra of Green Fluorescent Protein Chromophore,” Russian Journal of Physical Chemistry B, Focus on Physics, Vol. 2, No. 5, 2008, pp. 671-675. doi:10.1134/S1990793108050023
- M. A. L. Marques and E. K. U. Gross, “Time-Dependent Density Functional Theory,” Annual Review of Physical Chemistry, Vol. 55, 2004, pp. 427-455.
- M. C. Zerner, K. B. Lipkowitz, and D. B. Boyd, “Semi Empirical Molecular Orbital Methods,” Reviews in Computational Chemistry, Vol. 2, 1991, pp. 313-366. doi:10.1002/9780470125793.ch8
- P. E. M. Siegbahn and F. Himo,“The Quantum Chemical Cluster Approach for Modeling Enzyme Reactions,” Wiley Interdisciplinary Reviews: Computational Molecular Science, Vol. 1, No. 3, 2011, pp. 323-336. doi:10.1002/wcms.13
- K. A. Lukyanov, A. F. Fradkov, N. G. Gurskaya, M. V. Matz, Y. A. Labas, A. P. Savitsky, M. L. Markelov, A. G. Zaraisky, X. Zhao, Y. Fang, W. Tan and S. A. Lukyanov, “Natural Animal Coloration Can Be Determined by a Nonfluorescent Green Fluorescent Protein Homolog,” The Journal of Biological Chemistry, Vol. 275, No. 34, 2000, pp. 25879-25882. doi:10.1074/jbc.C000338200
- D. M. Chudakov, V. V. Belousov, A. G. Zaraisky, V. L. Novoselov, D. B. Staroverov, D. B. Zorov, S. A. Lukyanov and K. A. Lukyanov, “Kindling Fluorescent Proteins for Precise in Vivo Photolabeling,” Nature Biotechnology, Vol. 21, No. 2, 2003, pp. 191-194. doi:10.1038/nbt778
- D. M. Chudakov, A. V. Feofanov, N. N. Mudrik, S. Lukyanov and K. A. Lukyanov, “Chromophore Environment Provides Clue to Kindling Fluorescent Protein Riddle,” The Journal of Biological Chemistry, Vol. 278, No. 9, 2003, pp. 7215-7219. doi:10.1074/jbc.M211988200
- M. L. Quillin, D. M. Anstrom, X. Shu, S. O’Leary, K. Kallio, D. M. Chudakov and S. Remington, “Kindling Fluorescent Protein from Anemonia sulcata: Dark-State Structure at 1.38 Å Resolution,” Biochemistry, Vol. 44, No. 15, 2005, pp. 5774-5787. doi:10.1021/bi047644u
- M. Andresen, M. C. Wahl, A. C. Stiel, F. Gräter, L. V. Schäfer, S. Trowitzsch, G. Weber, C. Eggeling, H. Grubmüller, S. W. Hell and S. Jakobs, “Structure and Mechanism of the Reversible Photoswitch of a Fluorescent Protein,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 102, No. 37, 2005, pp. 13070-13074. doi:10.1073/pnas.0502772102
- P. G. Wilmann, J. Petersen, R. J. Devenish, M. Prescott and J. Rossjohn, “Variations on the GFP Chromophore: A Polypeptide Fragmentation within the Chromophore Revealed in the 2.1-Å Crystal Structure of a Nonfluorescent Chromoprotein from Anemonia sulcata,” The Journal of Biological Chemistry, Vol. 280, No. 4, 2005, pp. 2401- 2404. doi:10.1074/jbc.C400484200
- T. A. Schüttrigkeit, T. von Feilitzsch, C. K. Kompa, K. A. Lukyanov, A. P. Savitsky, A. A. Voityuk and M. E. Michel-Beyerle, “Femtosecond Study of Superlinear Light Induced Fluorescence Increase of the Coral Protein asFP595,” Chemical Physics, Vol. 323, No. 2-3, 2006, pp. 149-160. doi:10.1016/j.chemphys.2005.09.039
- J. Nathan Henderson and S. J. Remington, “The Kindling Fluorescent Protein: A Transient Photoswitchable Marker,” Physiology, Vol. 21, No. 3, 2006, pp. 162-170.
- Y. A. Tretyakova, A. A. Pakhomov and V. I. Martynov, “Chromophore Structure of the Kindling Fluorescent Pro tein asFP595 from Anemonia sulcata,” Journal of the American Chemical Society, Vol. 129, No. 25, 2007, pp. 7748- 7749. doi:10.1021/ja071992c
- A. L. Rusanov, T. V. Ivashina, L. M. Vinokurov, I. I. Fiks, A. G. Orlova , I. V. Turchin, I. G. Meerovich and V. V. Zherdeva, A. P. Savitsky, “Lifetime Imaging of FRET between Red Fluorescent Proteins,” Journal of Biophotonics, Vol. 3, No. 12, 2010, pp. 774-783. doi:10.1002/jbio.201000065
- A. P. Savitsky, A. L. Rusanov, V. V. Zherdeva, T. V. Gorodnicheva, M. G. Khrenova and A. V. Nemukhin, “FLIMFRET Imaging of Caspase-3 Activity in Live Cells Using Pair of Red Fluorescent Proteins,” Theranostics, Vol. 2, No. 2, 2012, pp. 215-226. doi:10.7150/thno.3885
- B. L. Grigorenko, A. V. Nemukhin, I. A. Topol and S. K. Burt, “Modeling of Biomolecular Systems with the Quantum Mechanical and Molecular Mechanical Method Based on the Effective Fragment Potential Technique: Proposal of Flexible Fragments,” The Journal of Physical Chemistry A, Vol. 106, No. 44, 2002, pp. 10663-10672. doi:10.1021/jp026464w
- A. V. Nemukhin, B. L. Grigorenko, I. A. Topol and S. K. Burt, “Flexible Effective Fragment QM/MM Method: Validation through the Challenging Tests,” Journal of Computational Chemistry, Vol. 24, No. 12, 2003, pp. 1410-1420. doi:10.1002/jcc.10309
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr., “General Atomic and Molecular Electronic Structure System,” Journal of Computational Chemistry, Vol. 14, No. 11, 1993, pp. 1347-1363. doi:10.1002/jcc.540141112
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. G. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. AlLaham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, “Gaussian 03, Revision C.02,” Gaussian, Inc., Wallingford, 2004.
- Q. Wang, L. J. Byrnes, B. Shui, U. F. Röhrig, A. Singh, D. M. Chudakov, S. Lukyanov, W. R. Zipfel, M. I. Kotlikoff and H. Sondermann, “Molecular Mechanism of a GreenShifted, pH-Dependent Red Fluorescent Protein mKate Variant,” PLOS ONE, Vol. 6, No. 8, 2011, p. e23513. doi:10.1371/journal.pone.0023513
- I. Topol, J. Collins, A. Savitsky and A. Nemukhin, “Modeling Absorption of the Kindling Fluorescent Protein with the Neutral Form of the Chromophore,” International Journal of Quantum Chemistry, Vol. 112, No. 17, 2012, pp. 2947-2951. doi:10.1002/qua.24134
NOTES
*Corresponding author.

