American Journal of Analytical Chemistry
Vol.08 No.01(2017), Article ID:73282,16 pages
10.4236/ajac.2017.81003
The Thermal Decomposition of Ammonium Meta-Vanadate under Restricted Flow Conditions
Lori R. Brock, Jeff W. Keister, Michelle France, Nathan Fierro, Thomas C. DeVore
Department of Chemistry, James Madison University, Harrisonburg, VA, USA

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 2, 2016; Accepted: January 1, 2017; Published: January 4, 2017
ABSTRACT
The products obtained during the thermal decomposition of ammonium meta-vanadate depend on the configuration of the container, the mass of the sample, the heating rate and the composition of the carrier gas. The decomposition in an uncapped container produced (NH4)2V4O11, NH4V3O8, and V2O5 as the apparent stable products while the products in a capped container were NH4V3O8, and V2Ox where x was between 4 and 5. These differences are attributed to the different amounts of the evolved gases in the cell. EGA-FTIR clearly established that the reduced final product in the capped cell resulted from a reaction between NH3 and the V2O5 formed during the decomposition. A pre-equilibrium kinetics model where the rate of the reverse reaction depends on the partial pressure of the gaseous products in the cell could explain the different reaction intermediates. This model provides a possible explanation for the different apparent activation energies that have been reported for the thermal decomposition of other compounds where a reversible step could occur in the decomposition mechanism.
Keywords:
Ammonium Meta-Vanadate, Thermal Decomposition, Kinetics, Activation Energy

1. Introduction
Simple reactions are those where one solid compound decomposes to form a second solid compound plus one or more gaseous compound in one step. The goal of kinetics investigations
A(s) ó B(s) + C(g) (1)
is to establish the activation energy, the A factor, and a mechanistic expression for the decomposition usually denoted as i(α) and g(α). This set of parameters is often called “the kinetic triplet.” [1] - [17] . There has been considerable debate about the best method for obtaining the kinetic triplet [1] - [17] . In an effort to mitigate these problems, several “new” approaches have been presented for obtaining the kinetic triplet during the past 15 years to obtain more reliable data as shown by [8] - [17] and the references therein. Often, these new methods have established that the “simple decompositions” occur through several mechanistic steps. The ICTAC committee has critically evaluated these approaches and has made several recommendations for obtaining and analyzing thermal analysis data [16] [17] . The model free methods were determined to be valuable methods for identifying multiple step processes and they recommended using it in combination with model fitting approaches to determine the kinetic parameters. They also recommended using at least two different sample sizes and two different heating hates to determine if the Arrhenius parameters determined are independent of the experimental conditions.
One example where different values for the activation energy, different intermediates, and different final products have been reported is illustrated by the thermal decomposition of ammonium meta-vanadate (AMV) reported in Table 1 [18] - [24] . Since the thermal decomposition of AMV is a convenient source of
Table 1. Observed reaction orders, stable products, activation energies (E), and temperature ranges for the thermal decomposition of NH4VO3 under various experimental conditions.
vanadium processing, it has been investigated under many different sets of experimental conditions [18] - [24] . As shown in Table 1, different experimental conditions produce different results [18] - [24] . In 1992, Maciejewski showed that the mass of the solid reactant, the surrounding atmosphere, the carrier gas flow rate, the heating rate, and chemical interactions between the gaseous and the solid products changed the apparent kinetic parameters observed for this reaction [18] . Both Wunjun et al. [23] and Biedunkiewicz et al. [24] reported that increasing the heating rate or the sample size decreased the resolution of the first two transitions hindering the model free analyses. No clear explanations for these observations have been presented. Wahlbeck has presented a possible explanation for the apparent disparities related to the carrier gas flow when he showed TGA data can be analyzed with the transpiration theory used in the Ruff experiment. Since the mass of the carrier gas and the flow rate are included in these equations, the differences in the apparent activation energies caused by these parameters could be explained using this approach [25] . However, the results that he presented assume an equilibrium process and give ΔH not E for the reaction. This contrasts dramatically with the usual assumption that the solid state thermal decomposition occurred far from equilibrium and that the reverse reactions can be ignored during the analysis [1] - [18] [26] . Biedunkiewicz et al. [24] have presented evidence for chemical reactions between the surrounding atmosphere and the solid residue that will obviously change the products observed. Differing rates of these gas surface reactions are also a possible explanation for the different activation energies reported in Table 1. Slowing the rate of transport of the gaseous products would allow more time for secondary reactions to occur and could provide an easy way to check for possible gas surface reactions. The thermal decomposition of AMV has been investigated under restricted flow conditions to try to determine if these secondary reactions are the cause of the different results for the decomposition of AMV presented in Table 1. Isothermal and non-isothermal thermal gravimetric (TG) methods using capped and uncapped cells were used to measure the dynamics for the thermal decomposition of AMV. Evolved gas analysis-FTIR (EGA-FTIR) under vacuum in a closed IR cell was done to look for evidence of secondary reactions. This manuscript presents the results of this investigation.
2. Experimental
Thermal gravimetric analysis (TGA) data were obtained using a Mettler-Toledo SDTA851e in flowing nitrogen (purge rates were set at 150 mL∙min−1 and the protection flow rate was 50 mL∙min−1). Both isothermal and non-isothermal methods were used to investigate the dynamics of the AMV decomposition. Non-isothermal investigations were done using heating rates ranging from 1 to 40 degrees per minute. Ten (10) mg samples of Fischer Purified AMV powder were placed in the 70 μl alumina crucibles available from Mettler-Toledo for all experiments reported here. Experiments were done with and without the alumina caps that come with these cells to vary the rate of transport of the gaseous products from the cell.
Evolved gas analysis-Fourier transform infrared (EGA-FTIR) was done using a home built apparatus that has been described in detail previously [26] [27] [28] and is shown schematically in Figure 1. The IR cell was constructed by using rubber O-rings to attach KBr windows to opposing ends of a MDC four-way cross vacuum flange to form the optical path. One of the remaining ends was connected to the vacuum line through a stainless steel valve that can be closed to isolate the cell from the vacuum. The remaining end of the flange was attached to the sample cell constructed from a 25 cm long piece of 9 mm glass tubing that had been sealed on one end. The furnace assembly was made by wrapping a 12 mm OD quartz tube with nichrome heating wire and covering the wire with thermal insulation. A BK Precision High Current DC Regulated Power Supply provided power to the furnace. Both isothermal and non-isothermal heating are possible with this apparatus.
The IR cell was placed in the sample chamber of a Nicholet Magna 750 FTIR. The spectrometer was set to collect one spectrum (2 scans) from 4000 to 400 cm−1 with 4 cm−1 resolution every 2 seconds for the 60 minute duration of the experiment. Spectral assignments were made by comparing the observed spectrum to spectra stored in the Nicholet-Aldrich spectral library. Integrated intensities of the selected bands were used to determine the relative amounts of products produced during each step of the reaction. The integrated intensities can be used to determine the extent of reaction (α) using Equation (2). In Equation (2), It is the intensity at time t and Imax is the intensity when all of the compound has reacted.
Figure 1. Schematic of the IR cell used to do EGA-FTIA.
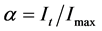 (2)
(2)
3. Results and Discussion
3.1. EGA-FTIR
The EGA-FTIR using a dynamic vacuum indicated that ammonia and water were lost throughout the decomposition (see Figure 2). If the ammonia were allowed to remain in contact with the V2O5 at temperatures above 470 K, the absorbance of the ammonia bands decreased and IR bands arising from N2O were observed (see Figure 2 and Figure 3). XRD of the residue also indicated that
Figure 2. The IR spectra observed as NH4VO3 thermally decomposed in the IR cell isolated from vacuum. The identity of the IR bands and the decomposition temperatures are given in the figure.
Figure 3. EGA-FTIR profiles for the loss of NH3 from NH4VO3 in the cell isolated from vacuum. The profile for the formation of N2O from the reaction between NH3 and V2O5 is also shown.
reduced vanadium oxide had formed as the V2O5 and NH3 reacted. This explains why VO2 was produced in an NH3 atmosphere and supports the conclusions reached by Biedunkiewicz et al. [24] that the exotherm at 630 K during the decomposition of AMV in dry air is from the oxidation of a reduced vanadium residue. This provides clear evidence that a secondary reaction between the decomposition products can affect the apparent reaction mechanism. Kinetic analysis based upon only mass loss data under the normal assumption that only one decomposition reaction is occurring would give different results as the rate of transport of the gaseous products from the reaction region change. In this case, the secondary reaction produces a larger mass loss than the ideal mass loss from the thermal decomposition of AMV in inert atmospheres.
As shown in Figure three, the ammonia appeared to be lost in two steps under these conditions. Since the oxidation of occurs during the second decomposition step, the kinetics for the initial reaction was the only one investigated in detail. Analysis using the EGA data for this reaction (assumed to be (3)) was determined by monitoring the amount of ammonia in the cell and using Equation (2) to monitor the extent of reaction.
3NH4VO3 → NH4V3O8 + 2 NH3 + H2O (3)
After 50 minutes, the temperature was rapidly increased to determine the absorbance of the ammonia when the sample had completely decomposed as shown in Figure 4. Analyses were done for α < 0.3 in this investigation. Analysis was done following the procedures typically used for TGA data [29] [30] . As shown in Figure 5, the first order rate equation fit the data well. The Arrhenius constants determined by repeating the experiment at several temperatures were 125 ± 10 kJ∙mol−1 and 2 × 1011 s−1 for E and A respectively (see Figure 6). The activation energy determined is within experimental error of the values reported in vacuum
Figure 4. An EGA profile of the amount of NH3 collected in the closed evacuated IR cell from the thermal decomposition of NH4VO3 at 425 K. The rapid intensity increase at 50 minutes resulted from rapidly heating the NH4VO3 to totally decompose the compound.
Figure 5. Model fit of the rate data given in Figure 3. The ln(1-A/AMAX) indicates first order kinetics. The rate constant is given by the slope.
Figure 6. Arrhenius plot determined for the thermal decomposition of NH4VO3 a under static atmosphere of the reaction products using the rate constants determined from the method illustrated in Figure 5.
(129 kJ∙mol−1) and in air (131 kJ∙mol−1), but is somewhat less than the values in nitrogen and argon reported previously for the formation of NH4V3O8 [18] - [24] . Most of the previous investigations indicated that the reaction followed the AE-2 mechanism. While the AE-2 mechanism did fit this data reasonable well, first order was better for the limited range of alpha investigated.
3.2. TGA
As shown in Figure 7, TGA obtained for the thermal decomposition of NH4VO3 using an uncapped and a capped cell under identical nitrogen flows, sample sizes and heating rates were clearly different. The results are summarized in Table 2. The decomposition in an uncapped cell produced an intermediate, (NH4)2V4O11, that was not observed in the capped cellor the EGA experiments. NH4V3O8 was formed under both sets of conditions. Both results are consistent with the Raman spectroscopic investigation of AMV reported by Twu et al. [31] and many of the previous investigations summarized in Table 1. The final products were also different with more total mass loss observed in the capped cell. Both Biedunkiewicz et al. [24] and Wanjun et al. [25] reported a similar finding from increasing the heating rate. The first two transitions that are clearly separated at a heating rate of 2 K/min are barely resolved at rates of 10 K/min. Wanjun et al. [25] also reported that a similar finding as the sample size increased. All of these differences could be from differences in the transport rate of the gaseous products from the cell since faster heating rates and larger sample sizes are also expected to have a higher vapor pressure of the gaseous product in the cell. The
Figure 7. The TGA and DTG profiles observed for the thermal decomposition of NH4VO3 using capped and uncapped 70 μl alumina cells using non-isothermal conditions. All other experimental variables were the same.
Table 2. The percent mass losses observed for the thermal decomposition of NH4VO3 under open and closed cell conditions. Data were averaged for heating rates of 5 and 10 degrees per minute under 50 ml/min of nitrogen carrier gas.
different final products result from the reaction between V2O5 and NH3 as observed in the EGA-FTIR experiments. Slowing the rate of transport by using a capped cell allows the gases to remain in the cell allowing time for the secondary reactions to occur. The failure to observe (NH4)2V4O11 in the capped cell, the static atmosphere EGA experiments, or when the heating rate or sample size increased suggest that the formation of this compound was inhibited by the presence of gaseous products in the cell.
Several methods for determining the reaction kinetics from TGA data using both isothermal and non-isothermal methods have been developed [1] - [24] . The isoconversion activation energies determined using the Sterik method for the “first step” in the decomposition assuming that NH4V3O8 was the only product are presented in Figure 8. The measurements in capped and uncapped cells produced similar results. The values determined in an uncapped cell decreased from 156 kJ/mole to 133 kJ/mol as the extent of reaction (α) goes from 0.05 to approximately 0.7. At α = 0.7, the apparent activation energy increased to approximately 200 kJ/mol. The apparent activation energy in the capped cell was approximately constant at 133 kJ/mol for 0.15 < α < 0.7. After α = 0.7 it increased to a value of 147 kJ/mol. The rapid increase is a clear indication that there was a change in the mechanism. This is not surprising since (NH4)2V4O11 was probably produced initially even though it was not observed in all of the TG’s. The trend observed for α < 0.7 for the uncapped cell is similar to the trend in the isoconversion values for step 1 reported by Wanjun et al. [23] The smaller values found here (133 kJ/mol compared to 150 kJ/mol) results from not adjusting the alpha values to give a (NH4)2V4O11 as the product. The decreasing trend is an indication that the reaction is reversible and that the amount of gaseous product in the cell increases as the reaction proceeds producing a lower effective activation energy [16] .
The isothermal curves obtained for 60 minute decompositions for AMV decompositions between 400 K and 475 K in capped and uncapped cells are shown
Figure 8. The activation energies for the “first peak” of the thermal decomposition of NH4VO3 from an uncapped and a capped cell using the Sterik method.
in Figure 9 and Figure 10. As with the non-isothermal data, decompositions in the uncapped cell clearly indicated (NH4)2V4O11 at all temperatures. The capped cell decompositions also indicated this compound at 450 K, but gave no indication of it at higher temperatures. Consistent with most of the previous results, the best model fit for this data was found to be Avarami-Erofe’ev equation with n = 2 as shown in Figure 11. The activation energy determined for the initial peak using this approach was ~125 kJ/mol for the uncapped cells and ~115 kJ/mol for the capped cells. Both are consistent with the EGA results and in fair agreement with the model free results presented above.
Figure 9. Constant temperature mass loss profiles for the thermal decomposition of NH4VO3 from an uncapped cell. The decomposition temperatures are given in the figure.
Figure 10. Constant temperature mass loss profiles for the thermal decomposition of NH4VO3 from a capped cell. The decomposition temperatures are given in the figure.
Figure 11. Examples of the best fit of the constant temperature data (T = 435 K) for the thermal decomposition of NH4VO3 from an open cell using the Avarami-Erofe’ev equation with n = 2.
3.3. Alternative Kinetic Analysis
Although the activation energies determined for all of these approaches were similar, there was no obvious way to explain the different intermediates observed, the different kinetic models needed to fit each different type of experiment, and the varying activation energies indicated by the model free analysis. While it is reasonable to assume that more than one reaction was occurring and that the contribution made by each was changing as the reaction progressed, neither the model free model nor the model fitting offer insight into the chemical processes that are producing these changes. An alternative model, based upon the pre-equilibrium model used for gas phase kinetics was developed and tested to determine if it could be used to explain this data. In it, the reaction was assumed to proceed through an intermediate in equilibrium with the starting material following a reaction sequence such as:
AMV → I + NH3 (4)
NH3 + I → AMV (5)
I → P + NH3 + H2O (6)
where I is an unspecified intermediate and P is the product of that step of the reaction. Assuming that (4) follows first order kinetics and (5) is proportional to I (assumed to be proportional to α) and the pressure of NH3 in the cell, the change in mass is related to the extent of reaction by
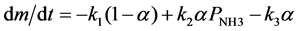 (7)
(7)
In a closed cell at equilibrium, PNH3 would depend on α, so it is reasonable to assume that PNH3 is also proportional to α under the restricted flow conditions used here. If so,
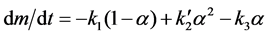 (8)
(8)
where 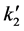 also contains the relationship between PNH3 and α.
also contains the relationship between PNH3 and α.
The fit for the open cell data at 430 K for the formation of (NH4)2V4O11 obtained using this model is shown in Figure 12. The rate constants obtained were k1 = 0.0148 mg/min, 

Figure 12. Least squares fit of the data for the isothermal decomposition of NH4VO3 from an open cell at 430 K determined using the pre-equilibrium model. The rate constants determined were k1 = 0.0148 mg/min, k2 = 0.0732 mg/min, and k3 = 0.0780 mg/min.
Figure 13. Arrhenius plots for rate constants determined for the thermal decomposition of NH4VO3 using the pre-equilibrium model. The activation energies determined were E1 ~ 170 kJ/mol, E2~ 45 kJ/mol, E3 ~ 85 kJ/mol.
fitting methods and is in reasonable agreement with the capped cell model free value. The value for the forward step is consistent with the larger values reported reflecting the conditions where the maximum mass lost id expected. While this analysis was done under conditions where P was (NH4)2V4O11 and the intermediate was not specified, it is clear that it could be extended to include multiple reversible reactions. Products under one set of conditions could become intermediates when the conditions change as seems to be the case for (NH4)2V4O11.
4. Conclusions
The dynamics observed for the thermal decomposition of ammonium metavanadate depend upon the rate of transport of the gaseous products away from the reaction zone. The different products observed for factors such as cell design, sample size and packing, and the type and flow rate of the carrier gas most likely result from this effect. It is likely that the difference in reaction dynamics reported for other reversible reactions (see [1] - [18] ) could result from a similar effect. It is relatively easy to determine if the gaseous products are affecting the reaction dynamics by changing the sample size, the heating rate, or the cell configuration as recommended by the ICTAC Kinetics Committee [16] [17] . These recommendations should be followed if a complete understanding of the reaction dynamics is desired.
A pre-equilibrium model that incorporated an unspecified intermediate fit the mass loss data reasonably well and provides an explanation for the different intermediates that have been reported for the decomposition of AMV. When the gaseous products are rapidly removed from the cell, the rate of the reverse reaction is slow since its rate likely involves the intermediate and at least one of the gaseous products. If the relative rate of formation of the intermediate becomes faster than its rate of destruction, its concentration can increase to observable levels. When the rate of the reverse reaction is relatively fast, its concentration is below the detection limit and it is not observed. This model also provides a possible explanation for variable activation energies if the concentration of the gaseous products changes as the reaction proceeds. This would change the measured rate of mass loss. Since heating rate influences the rate of mass transfer from the cell, the apparent activation energy determined would change. For an equilibrium process this effect usually produces a decreasing apparent activation energy as the extent of reaction increases [16] .
It is probably overly optimistic to assume that either the correct mechanism or the activation energies for the fundamental reactions have been determined exactly. Although the first order pre-equilibrium model used provided a reasonable fit to the data, other models such as one of the diffusion mechanism may be more appropriate since vapor transport obviously plays a role in the mechanism. However, what is clear from this investigation is that the reaction between the vapor species and the condensed phase affects the observed products and dynamics for the decomposition of AMV. This reaction proceeds through a multi-step mechanism that could have several intermediates. By simply placing a cap on the cell the dynamics changed enough to produce different apparent stable intermediates. It is likely that gas surface reactions contribute to other simple thermal decomposition mechanisms and the possibility of the reverse reaction contributing to the mechanism should not be dismissed without evidence that it is reasonable to do so. Although it may not be necessary to understand every aspect of the dynamics to apply this process to device manufacturing, these results show that assuming measurements made under one set of conditions will work for all sets of conditions could produce unexpected results.
Acknowledgements
The authors wish to thank the National Science Foundation (NSF-REUCHE- 0097448, NSF-REU-CHE-0097449, NSF-REU-CHE-0353807 and NSF-REU- CHE-1461175) and the US Department of Defense ASSURE program, grant #0353773 for partial support of this project and NSF-CHE-0076685 for providing the funds needed to purchase the Mettler Toledo TGA.
Cite this paper
Brock, L.R., Keister, J.W., France, M., Fierro, N. and DeVore, T.C. (2017) The Thermal Decomposition of Ammonium Meta-Vanadate under Restricted Flow Conditions. American Journal of Ana- lytical Chemistry, 8, 35-50. http://dx.doi.org/10.4236/ajac.2017.81003
References
- 1. Brown, M.E. (1997) Steps in a Minefield: Some Kinetic Aspects of Thermal Analysis. Journal of Thermal Analysis, 49, 17-32.
https://doi.org/10.1007/bf01987418 - 2. Galwey, A.K. and Brown, M.E. (2000) Solid-State Decompositions—Stagnation or Progress? Journal of Thermal Analysis, 60, 863-877.
https://doi.org/10.1023/A:1010107724523 - 3. Sewry, J.D. and Brown, M.E. (2002) “Model-Free” Kinetic Analysis? Thermochimica Acta, 390, 217-225.
https://doi.org/10.1016/S0040-6031(02)00083-7 - 4. Opfermann, J.R., Kaisersberger, E. and Flammersheim, H.J. (2002) Model-Free Analysis of Thermoanalytical Data-Advantages and Limitations. Thermochimica Acta, 391, 119-127.
https://doi.org/10.1016/S0040-6031(02)00169-7 - 5. Khawam, A. and Flanagan, D.R. (2005) Role of Isoconversional Methods in Varying Activation Energies of Solid-State Kinetics: I. Isothermal Kinetic Studies. Thermochimica Acta, 429, 93-101.
https://doi.org/10.1016/j.tca.2004.11.030 - 6. Khawam, A. and Flanagan, D.R. (2005) Role of Isoconversional Methods in Varying Activation Energies of Solid-State Kinetics: II. Nonisothermal Kinetic Studies. Thermochimica Acta, 429, 101-112.
https://doi.org/10.1016/j.tca.2005.05.015 - 7. Galwey, A.K. (2003) What Is Meant by the Term “Variable Activation Energy” When Applied in the Kinetic Analyses of Solid State Decompositions (Crystolysis Reactions)? Thermochimica Acta, 397, 249-268.
https://doi.org/10.1016/S0040-6031(02)00271-X - 8. Zhou, D. and Grant, D.J. (2004) Model Dependence of the Activation Energy Derived from Non-Isothermal Kinetic Data. The Journal of Physical Chemistry A, 108, 4239-4246.
https://doi.org/10.1021/jp037917f - 9. Khawam, A. and Flanagan, D.R. (2005) Complementary Use of Model-Free and Modelistic Methods in the Analysis of Solid-State Kinetics. The Journal of Physical Chemistry B, 109, 10073-10080.
https://doi.org/10.1021/jp050589u - 10. Chen, H., Liu, N. and Fan, W. (2006) A New Method to Explain the Model Dependence of Apparent Activation Energy Derived from a Single Nonisothermal Dynamic Curve, Polymer. Degradation and Stability, 92, 1726-1730.
https://doi.org/10.1016/j.polymdegradstab.2005.12.007 - 11. Khawam, A. and Flanagan, D.R. (2006) Solid-State Kinetic Models: Basics and Mathematical Fundamentals. The Journal of Physical Chemistry B, 110, 17315-17328.
https://doi.org/10.1021/jp062746a - 12. Tan, G., Tang, D., Mu, T., Xu, C., Wang, D. and Wang, Q. (2014) The Validity on Nonleaner Isocoversional Method in the Kinetic Analysis of Calcium Carbonate Decomposition under Isothermal and Non-Isothermal Conditions. Thermochimica Acta, 585, 21-24.
https://doi.org/10.1016/j.tca.2014.03.041 - 13. Burnham, A.K. (2014) Obtaining Reliable Phenomenological Chemical Kinetic Models for Real-World Applications. Thermochimica Acta, 597, 35-40.
https://doi.org/10.1016/j.tca.2014.10.006 - 14. Sestak, J. (2015) The Quandary Aspects of Non-Isothermal Kinetics beyond the ICTAC Kinetic Committee Recommendations. Thermochimica Acta, 611, 26-35.
https://doi.org/10.1016/j.tca.2015.04.026 - 15. Mianowski, A. and Urbanczyk, W. (2016) Thermal Dissociation in Terms of the Second Law of Chemical Thermodynamics. Journal of Thermal Analysis and Calorimetry, 126, 863-870.
- 16. Vyazovkin, S., Burnham, A.K., Criado, J.M., Pérez-Maqueda, L.A., Popescu, C. and Sbirrazzuoli, N. (2011) ICTAC Kinetics Committee Recommendations for Performing Kinetic Computations on Thermal Analysis Data. Thermochimica Acta, 520, 1-19.
https://doi.org/10.1016/j.tca.2011.03.034 - 17. Vyazovkin, S., Chrissafis, K., Di Lorenzo, M.L., Koga, N.M., Pijolat, M., Roduit, B., Sbirrazzuoli, N. and Suñol, J.J. (2014) ICTAC Kinetics Committee Recommendations for Collecting Experimental Thermal Analysis Data for Kinetic Computations. Thermochimica Acta, 590, 1-23.
https://doi.org/10.1016/j.tca.2014.05.036 - 18. Maciejewski, M. (1992) Somewhere between Fiction and Reality—The Usefulness of Kinetic Data of Solid-State Reactions. Journal of Thermal Analysis, 38, 51-70.
https://doi.org/10.1007/BF02109108 - 19. Brown, M.E. and Stewart, B.V. (1970) The Thermal Decomposition of Ammonium Metavanadate, I—The Stoichiometry of the Decomposition. Journal of Thermal Analysis, 2, 287-299.
https://doi.org/10.1007/BF01911410 - 20. Brown, M.E., Glasser, L. and Stewart, B.V. (1972) The Thermal Decomposition of Ammonium Metavanadate II—The Kinetics and Mechanism of the Decomposition. Journal of Thermal Analysis, 6, 529-541.
https://doi.org/10.1007/BF01911558 - 21. Brown, M.E., Glasser, L. and Stewart, B.V. (1973) The Thermal Decomposition of Ammonium Metavanadate, III—A Structural View of the Decomposition Mechanism. Journal of Thermal Analysis, 7, 125-137.
https://doi.org/10.1007/BF01911632 - 22. Askar, M.H., Girgis, B.S. and Khilla, M.A. (1989) Activation Energy of the Thermal Decomposition of Ammonium Metavanadate. A Thermogravimetric Study. Journal of Thermal Analysis, 35, 1315-1324.
https://doi.org/10.1007/BF01912907 - 23. Wanjun, T., Yuwen, L., Xi, L. and Cunxin, W. (2004) Kinetic Studies of the Calcination of Ammonium Metavanadate by Thermal Methods. Industrial & Engineering Chemistry Research, 43, 2054-2058.
https://doi.org/10.1021/ie030418g - 24. Biedunkiewicz, A., Gabreil, U. and Figiel, P. (2012) Investigations on NH4VO3 Thermal Decomposition in Dry Air. Journal of Thermal Analysis and Calorimetry, 108, 965-970.
https://doi.org/10.1007/s10973-011-2149-6 - 25. Wahlbeck, P.G. (1992) TGA Experimental Data-Analysis Provided by Transpiration Theory. Thermochimica Acta, 197, 469-478.
https://doi.org/10.1016/0040-6031(92)85048-Z - 26. Pokol, G. (2000) Thermodynamic Driving Force in the Kinetic Evaluation of Thermoanalytical Curves. Journal of Thermal Analysis and Calorimetry, 60, 879-886.
https://doi.org/10.1023/A:1010159708593 - 27. DeVore, T.C. and Gallaher, T.N. (1984) Infrared Spectroscopic Investigation of the Reaction between SOCl2 and NO2. Inorganic Chemistry, 23, 3506-3509.
https://doi.org/10.1021/ic00190a014 - 28. Rhoten, M.C. and DeVore, T.C. (1997) Evolved Gas Analysis Investigation of the Reaction between Tris(2,4-Pentanedionato) Aluminum and Water Vapor in Chemical Vapor Deposition Processes to Produce Alumina. Chemistry of Materials, 9, 1757-1764.
https://doi.org/10.1021/cm960504p - 29. Crouch, M.A. and DeVore, T.C. (1996) Reaction between Bis(2,4-Pentanedio- nato)lead(II) and Water Vapor: A Thermodynamic Study. Chemistry of Materials, 8, 32-36.
https://doi.org/10.1021/cm950262d - 30. Brown, M.E. (1988) Introduction to Thermal Analysis. Chapman and Hall, New York.
https://doi.org/10.1007/978-94-009-1219-9 - 31. Twu, J., Shih, C.-F., Guo, I.-H. and Chen, K.-H. (1997) Raman Spectroscopic Studies of the Thermal Decomposition Mechanism of Ammonium Metavanadate. Journal of Materials Chemistry, 7, 2273-2277.
https://doi.org/10.1039/a702968c
















