Modeling and Numerical Simulation of Material Science
Vol.06 No.02(2016), Article ID:66181,13 pages
10.4236/mnsms.2016.62004
Constitutive Modelling of Elastomeric Seal Material under Compressive Loading
Ismail J. Abubakar, Peter Myler, Erping Zhou
School of Engineering, University of Bolton, Bolton, UK
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 January 2016; accepted 26 April 2016; published 29 April 2016
ABSTRACT
Elastomers are used in numerous engineering applications such as sealing components, it is therefore important to devise a method that can accurately predict elastomers’ response to load. Many applications that employ the use of these materials subject them to a nonlinear large strain; therefore the simple Hooke’s law is not sufficient to describe their material behaviour. This paper presents an approach to obtain material properties of elastomer under compression loading, based on hyperelastic strain formulation, through experimental test and finite element modelling. The paper focuses on the isotropic incompressible behaviour exhibited by elastomers, and obtains strain energy functions that satisfy the characteristic properties of a hyperelastic model. Data obtained from compression test on a nitrile rubber (NBR) specimen were used as material input into ABAQUS®―a finite element analysis software. A least square fitting technique was used to determine the coefficients of various stable hyperelastic models, based on Drucker’s stability criteria within the software. The strain energy functions obtained concentrate on material parameters which are related to physical quantities of the material molecular network they are subjected to in practical application. The approach benefits from mathematical simplicity, and possesses the property of the deformation mode dependency. Furthermore, a model validation procedure using a step-by-step method for parameters estimation is explained. The work herein is a nonlinear finite element modelling process that leads to an optimal solution and can be employed not only for elastomeric seals, but also for similar engineering assets.
Keywords:
Elastomer, Hyperelasticity, Elastomer Seal, Finite Element Modelling

1. Introduction
Elastomers are very unique visco-hyperelastic materials capable of accommodating large deformation and can recover completely when the load is removed. They possess damping characteristics (ability to dissipate energy), high strength especially under shear and compressive deformation, making them suitable for use in design of mechanical components associated with dynamic loading such as elastomeric lip seals.
Elastomeric seals are important machine components found in mechanical systems. There are currently hundreds of patented designs for elastomeric seals, it would be fair to say that practically all of them fall under the two categories of seals namely: static seal such as O-rings and dynamic seal e.g. radial lip seal. One of the application examples of the former is in hydraulic cylinder piston, where it is usually compressed to a desired level to achieve sealing as depicted in Figure 1 [1] - [3] . The latter on the other hand is illustrated in Figure 2, usually found in wind energy turbines, marine propulsion components etc. to provide an effective means of sealing a rotating shaft unit by preventing leakage of lubricant that inhibits excessive wear and to avoid penetration of external contaminants into the sealed fluid system [4] [5] . The important property which maintains an elastomeric seal for sealing applications is the resilience in an elastomer which provides a measure of speed of recovery when stress is released from the elastomer [6] [7] . The resilience therefore gives an indication of the ability of the seal to respond to dynamic movement.
The general concern in elastomeric seal design comes from how to understand the material properties, because this would be a useful tool from the view of safety and profitability to industries. One critical aspect of good design is appropriate material selection. This cannot be done without a comprehensive knowledge on how the material will behave when subjected to mechanical loads. Authors in [8] - [11] performed an evaluation of structural mechanics analysis in builtup stresses and deformations on the elastomeric seal profile using finite element analysis and modelling. Stress field, frictional wear and the contact pressure distribution were explored in their work.
The analysis and modelling of the dynamic response of an elastomeric component under compressive loading are essential and will facilitate the use of computer simulation for designing products that incorporate elastomers subjected to this type of load. However, the accuracy of such results will largely depend on the material property supplied for the analysis, considering that elastomers exhibit an incompressible behaviour with Poisson’s ratio value very close to 0.5, further compounded by a nonlinear stress-strain curve. Elastomers have a low modulus of elasticity (E) ranging from 10 MPa to 4 GPa (E-value for most metals is in the 50 - 400 GPa range), but very high elongation reaching up to 1000% (elongation for metals is always less than 100%) [12] . Being a
Figure 1. O-ring.
Figure 2. Radial lip seal running on shaft (a) cut-section (b) axisymmetric section.
visco-hyperelastic material, it comprises two components: the first corresponds to hyperelasticity based on a strain energy density function expressed in polynomial form to characterize quasi-static nonlinear response, while the second incorporates a relaxation-time function to capture rate sensitivity and strain history dependence. For an elastomer in compression without undergoing a cyclic loading, the viscous components can be ignored. However, FEA results can only be assumed reliable if there is a reasonable level of verification, most importantly in the Hyperelastic material parameter used.
This paper presents a methodology for evaluating the material property of an elastomer subjected to compression loads used in design of mechanical components, with a special interest in elastomeric seals.
Firstly the mechanics of linear elastic and hyperelastic materials is visited followed by experimental tests carried out on a lip seal elastomeric material (Acrylonitrile-butadiene rubber, NBR); the experimental test established the material property of the in-test specimen which can serve as design guide and validation. Data obtained from the experiment were then used to evaluate various hyperelastic models using commercial FEA package ABAQUS® to verify stability/suitability of the models while putting into consideration the elastomer’s material behaviour. A finite element model of the test specimen was reproduced and assigned the material parameters obtained from one of the suitable models while replicating an actual experimental condition. Results from the analysis were compared with the experimental tests and conclusions drawn.
2. Hyperelasticity
The stress-strain behaviour of elastomer remains elastic up to large strain (values often well over 300%) hence termed “hyperelastic material”. Elastomers exhibit a nonlinear elastic behaviour, which implies that its deformation is not directly proportional to the applied load. They however exhibit a Cauchy-elastic material behaviour like other simple elastic material which means that the stress at each point is determined only by the current state of deformation with respect to an arbitrary reference configuration and not the path or history of deformation [13] . The primary difference between a linear elastic material and a nonlinear hyperelastic material with respect to stress-strain relationship is that the latter derives its own from a strain energy density function whereas the former is derived from a constant factor [14] . Figure 3 depicts the stress-strain curve of a linear elastic material and a hyperelastic material.
The strain energy density W for hyperelastic material is way more complex to relate due to the complexity of rubber materials. An important approach in nonlinear elasticity theory for analysis of rubber-like materials is to derive a reasonable and applicable elastic law, which can form a key to the development of reliable analysis tool [13] .
There are several laws for strain energy potentials for hyperelastic materials; they define the strain energy stored in the material per unit of reference volume as a function of the strain energy at that point in the material based on the functions of the stretch invariants, 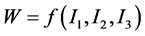 or stretch ratios
or stretch ratios  as in Figure 4.
as in Figure 4.
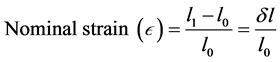 . (1)
. (1)

Figure 3. Stress-strain curve (a) linear elastic (b) hyperelastic.

Figure 4. Pure homogenous strain (a) unstrained state (b) strained state.
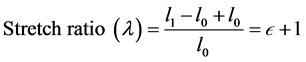 (2)
(2)
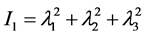 (3)
(3)
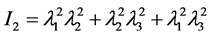 (4)
(4)
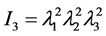 . (5)
. (5)
Hyperelastic Constitutive Model
The available phenomenological models of strain energy potentials for hyperelastic materials usually take a polynomial form. Thus
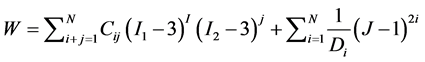 (6) [15]
(6) [15]
where,
W = Strain energy potential,
J = Elastic volume ratio,
I1, I2 = Stretch invariants,
N, Cij, Di = Material constants to be evaluated from tests data.
N.B. the material constants Cij, and Di describe the shear behaviour and compressibility of the material respectively.
J = 1; for complete incompressibility.
Some of the several forms of strain energy potentials available as seen in (Ghoreishy, 2012) are:
・ Mooney-Rivlin
The earliest and one of the significant phenomenological theories of hyperelasticity was proposed by Mooney later in conjunction with Rivlin. The model expresses strain energy as a function of elastic constant and first and second stretch invariants
 . (7)
. (7)
・ Neo-Hooke
The model is a special case of the Mooney-Rivlin form. If the material in the Mooney-Rivlin model has it value of C01 to be equal to zero, such material obeys Neo-Hookean model law:
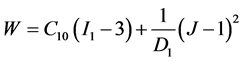 . (8)
. (8)
・ Ogden
Ogden’s proposed strain energy density function can be described directly in terms of principal stretch ratios as:
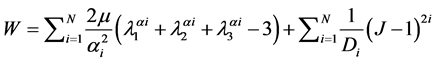 . (9)
. (9)
・ Yeoh
This is a special form of the reduced polynomial models. It is expressed as

・ Marlow
The Marlow model does not contain any explicit relation between strain energy density and/or invariants or stretch ratios. It is assumed that the strain energy density is only a function of the first invariant of the strain tensor

Since for incompressible materials, 


・ Arruda Boyce
This model has a slightly different form, it is not a phenomenological, but a micromechanical model, and it can be related thus

where, μ represents the initial shear modulus, λ is the stretch ratio, D represents the incompressibility parameter.
3. Experimental Test
To obtain the material properties of elastomer under compressive loading, a compression experimental test was adopted. In this study, an NBR (nitrile rubber) sample is used. NBR is the most widely used elastomers in industries as seal due to its moderate cost, excellent resistance to oils, fuels and grease over a wide range of temperature, possessing a good resistance to swelling by aliphatic hydrocarbons and ease of processing [6] . The test specimen is shown in Figure 5.
ASTM standard test method (ASTM: D575) was adopted. The test was performed on an INSTRON 3369 testing machine, a type of laser scanning extensometer which enables a non-contact strain measurement within the specimen during loading. The machine was set to operate in compression mode, using a 50-kN load cell. The overall test rig is presented in Figure 6.
A fixed flat plate is placed at the bottom of the test specimen whilst the plunger applies a compressive load on it. The NBR sample was allowed to deform freely, to mimic an in-process service of an elastomer seal in order to obtain its stress-strain plot. The experimental test result is provided in Figure 7.
4. Hyperelastic Material Parameters Evaluation
The test data obtained from stress strain curves of Figure 8 were used evaluate the suitability of four hyperelastic material models (Arruda-Boyce, Neo-Hooke, Ogden, and Yeoh) within Abaqus® software. A negative sign convention (-) was used to indicate in the data supplied, that the load was in compression and also the displacement of the specimen. The nonlinear curve fitting algorithm implemented in the software was used for this purpose. Figures 8-11 show the experimental Stress-Strain curves with their corresponding predicted characteristics for each hyperelastic models.

Figure 5. Compression test specimen (a) physical model, (b) CAD model (in mm), (c) plunger.

Figure 6. Experimental setup for compression test (a) test machine (b) compressed specimen.
Figure 7. Stress-strain curve of NBR test specimen under compression load.
As it can be seen, the models closely fit the experimental data. They give reasonable degree of agreements between real and computed data. The degree of fitting for the Yeoh model even though appears satisfactory from the plot, is however not recommendable for further use due to its unstable computed data as indicated from the evaluation report in Abaqus shown in Figures 12-15. To verify this, the stability of the selected material models was taken into consideration. ABAQUS makes this check using the Drucker Stability Postulate that implies the incremental internal energy of a material can only increase i.e.
Figure 8. Arruda-Boyce model vs. experiment.
Figure 9. Neo-Hooke model vs. experiment.

This means that the tangential stiffness matrix must be positive definite. Further evaluation indicated that Arruda-Boyce, Neo-Hooke and Ogden models were stable at all values of the strain supplied to it, while the Yeoh model was conditionally stable as indicated in Figure 15. The limiting strain in compression from the experimental test is 0.45 and for the Yeoh model falls out of this range. This implies that the use of this model will gives rise to unstable results even within the specified range. However, it is obvious that the limiting values for
Figure 10. Ogden model vs. experiment.
Figure 11. Yeoh model vs. experiment.
the other models were not only within the experimental values, but also within the values found in elastomeric seal applications as reported in [16] . For this reason, any of the stable models can be used for further modelling of an NBR elastomerseal within this strain range. The computed parameters for various stable model and unstable Yeoh model obtained from ABAQUS is shown in Table 1.
5. Finite Element Model
The extent to which a material model can work within a finite element analysis programme can be determined
Figure 12. Evaluated compression test data for stability check; Arruda Boyce model.
Figure 13. Evaluated compression test data for stability check; Neo Hooke model.
Figure 14. Evaluated compression test data for stability check; Ogden model.
Figure 15. Evaluated compression test data for stability check; Yeoh model.
Table 1. ABAQUS evaluated hyperelastic material parameters.
by modelling test specimen used to generate the experimental data. It is necessary to validate the hyperelastic parameters obtained in order to have confidence in modelling the elastomeric component through finite element analysis. Since Neo-Hooke, Ogden and Arruda Boyce model are stable in this study; these stable models were employed to validate the parameters obtained they also provide a good fit for compression mode of deformation [17] . For this reason, finite element modelling is carried out using Neo-Hooke, Ogden and Arruda Boyce material parameters to compare the analytical result with the test result in order to validate the models.
The test sample was modelled in ABAQUS® under the same uniaxial compression the sample experienced during the compression test. It is not necessary to model the whole component since both the geometry of the structure and the loading are axisymmetric. Therefore, it is only needed to model a plane through the component: each element represents a complete 360˚ ring. By adopting this approach, computational cost is well reduced in terms of possibility to use reduced number of elements for the analysis, reduced number of degrees of freedom, reduced run time and storage requirements for the analysis and allows the use of a more refined mesh.
For an incompressible material like elastomer, the volume cannot change under this loading. Therefore, the pressure stress cannot be computed from the displacements of the nodes; and, thus a pure displacement formulation is inadequate for an element with incompressible material behaviour. To take care of the incompressibility behaviour of elastomer, the Hybrid elements are used within Abaqus® in lieu of regular element because the pressure stress in the element is indeterminate.
Figure 16 shows the model of the analysis with the applied boundary conditions. Figure 17(a) shows the contour plot of the deformed specimen modelled. Table 2 presents a comparison of result obtained from the modelling and the corresponding experimental values.
The displacement at the metal base is zero, whereas, the deformable elastomeric component appears to displace downwards as depicted in Figure 17(b). The resultant displacement of the test specimen is presented in Figure 18.
Figure 16. Finite element modelling of compression test sample.
Figure 17. (a) Contour plot of the compressed NBR sample under a load of 423.40 KPa; (b) Nodal displacement plot.
Figure 18. Resultant displacement of test sample.
Table 2. FEA vs. Experimental result.
Table 2 demonstrates favourable agreement between the stable hyperelastic models and test data that can be used for further analysis, therefore indicating the potential of the models to describe behaviour of the elastomer over a prescribed strain.
6. Conclusions
In this work, a procedure for elastomer material parameter characterisation has been conducted through compression test and finite element modelling. The compression test is necessary in elastomer seal design study because it provides adequate information of an elastomer component in an in-service. In addition, the finite element modelling in this work puts into consideration material nonlinearity in lieu of the Hookean approximate. Experimental data from the tests were used to evaluate suitable hyperelastic constitutive models, and to obtain a set of material parameters that fits stress-strain response in a compression state. The Ogden, Neo-Hooke and Arruda Boyce models were found to be stable within the established strain boundary. They give a good description of the material with respect to the compressive loading imposed on the specimen. Furthermore, the implementation of stable models (Neo-Hooke, Arruda-Boyce and Ogden) into Abaqus® as an illustration to further model the test material shows good agreement between simulation and experimentation and thus can be used for design study of an elastomeric component in compression
In terms of future work, the hyperelastic model parameters obtained in this work will be implemented into an FEA, for the evaluation of structural mechanics analysis in built-up stresses and deformations on elastomeric rotary lip seal profile using finite element analysis. Stress field, frictional wear and the contact pressure distribution in an elastomeric will also be visited in future studies.
Cite this paper
Ismail J. Abubakar,Peter Myler,Erping Zhou, (2016) Constitutive Modelling of Elastomeric Seal Material under Compressive Loading. Modeling and Numerical Simulation of Material Science,06,28-40. doi: 10.4236/mnsms.2016.62004
References
- 1. Lin, C.K., Chen, T.T., Chyou, Y.P. and Chiang, L.K. (2007) Thermal Stress Analysis of a Planar SOFC Stack. Journal of Power Sources, 164, 238-251.
http://dx.doi.org/10.1016/j.jpowsour.2006.10.089 - 2. Singh, H.K. (2009) Lifetime Prediction and Durability of Elastomeric Seals for Fuel Cell Applications. Virginia Polytechnic Institute and State University, Virginia.
- 3. Clague, R., Marquis, A.J. and Brandon, N.P. (2012) Finite Element and Analytical Stress Analysis of a Solid Oxide Fuel Cell. Journal of Power Sources, 210, 224-232.
http://dx.doi.org/10.1016/j.jpowsour.2012.03.027 - 4. Tran, H. and Haselbacher, P. (2004) High-Performance Lift Augmentation Dynamic Seals for Turbine Bearing Compartments. Sealing Technology, 2004, 5-10.
http://dx.doi.org/10.1016/S1350-4789(04)00187-4 - 5. Boyce, M.P. (2012) Gas Turbine Engineering Handbook. Butterworth-Heinemann, New York.
- 6. Flitney, R. (2007) Seals and Sealing Handbook. 5th Edition, Elsevier, Oxford.
- 7. Liu, Y. (2013) Investigation on Elastomer Compatibility with Alternative Aviation Fuels. Doctor Thesis, The University of Sheffield, Sheffield.
- 8. Kim, C.K. and Shim, W.J. (1997) Analysis of Contact Force and Thermal Behaviour of Lip Seals. Tribology International, 30, 113-119.
http://dx.doi.org/10.1016/0301-679X(96)00030-8 - 9. Bignardi, C., Bertetto, M.A. and Mazza, L. (1999) Photoelastic Measurements and Computation of the Stress Field and Contact Pressure in a Pneumatic Lip Seal. Tribology International, 32, 1-13.
http://dx.doi.org/10.1016/S0301-679X(98)00106-6 - 10. Lee, C.-Y., Lin, C.-S., Jian, R.-Q. and Wen, C.-Y. (2006) Simulation and Experimentation of the Contact Width and Pressure Distribution of Lip Seals. Tribology International, 39, 915-920.
http://dx.doi.org/10.1016/j.triboint.2005.09.002 - 11. Kim, H.K., Park, S.H., Lee, H.G., Kim, D.R. and Lee, Y.H. (2007) Approximation of Contact Stress for a Compressed and Laterally One Side Restrained O-Ring. Engineering Failure Analysis, 14, Article ID: 16801692.
http://dx.doi.org/10.1016/j.engfailanal.2006.11.061 - 12. Crawford, R.J. (2012) Plastic Engineering. 3rd Edition, Butterworth-Heinemann, Oxford.
- 13. Treloar, L.G. (2005) The Physics of Rubber Elasticity. 3rd Edition, Oxford University Press, Glasgow.
- 14. Jakel, I.R. (2010) Analysis of Hyperelastic Materials with MECHANICA. PTC, Chemnitz.
- 15. ABAQUS (2013) Abaqus Analysis User’s Manual.
http://50.16.176.52/v6.13/ - 16. James, W. (2013) Compressive Strain [Interview] (09/12/2013).
- 17. Gent, A.N. (2012) Engineering with Rubber: How to Design Rubber Components. 3rd Edition, Hanser, Munich.
http://dx.doi.org/10.3139/9783446428713

















