Modeling and Numerical Simulation of Material Science
Vol.05 No.01(2015), Article ID:53092,11 pages
10.4236/mnsms.2015.51003
Prediction and Verification of Resistance Spot Welding Results of Ultra-High Strength Steels through FE Simulations
Oscar Andersson1, Arne Melander1,2
1Department of Production Engineering, KTH Royal Institute of Technology, Stockholm, Sweden
2Swerea KIMAB, Kista, Sweden
Email: oanderss@kth.se
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 November 2014; revised 8 December 2014; accepted 26 December 2014
ABSTRACT
Resistance spot welding (RSW) is the most common welding method in automotive engineering due to its low cost and high ability of automation. However, physical weldability testing is costly, time consuming and dependent of supplies of material and equipment. Finite Element (FE) simu- lations have been utilized to understand, verify and optimize manufacturing processes more effi- ciently. The present work aims to verify the capability of FE models for the RSW process by com- paring simulation results to physical experiments for materials used in automotive production, with yield strengths from approximately 280 MPa to more than 1500 MPa. Previous research has mainly focused on lower strength materials. The physical weld results were assessed using de- structive testing and an analysis of expulsion limits was also carried out. Extensive new determi- nation of material data was carried out. The material data analysis was based on physical testing of material specimens, material simulation and comparison to data from literature. The study showed good agreement between simulations and physical testing. The mean absolute error of weld nugget size was 0.68 mm and the mean absolute error of expulsion limit was 1.10 kA.
Keywords:
Resistance Spot Welding, FE Simulations, High Strength Steel, Material Modeling, Weld Size

1. Introduction
Resistance spot welding (RSW) is the primary joining method in automotive industry due to its low cost and high ability for automation. The main measures for evaluation of the RSW process are weld size, which is in- dicative of both tensile strength and process robustness, together with the occurrence of expulsion, which risks weld defects and damage to surrounding equipment.
The automotive industry is facing increasing demands for lightweight structures with maintained safety. An efficient solution to meet such demands is the introduction of high strength (HSS) and ultra high strength (UHSS, sometimes also referred to as advanced high strength steels, AHSS) in body-in-white components. While higher strength materials effectively enables reduction of car weight, the material behavior of HSS and UHSS, due to their metallurgy and alloying elements, also imposes challenges for joining in manufacturing [1] .
Numerical models are utilized to reduce costs for product verification and optimization in a multitude of fields including material processing. The first numerical analyses of the RSW process were published in the early 1960s. Both a one-dimensional model by Archer [2] and an axi-symmetrical model by Greenwood [3] were presented and calculated the temperature change in the weld zone. However, these early models were not capable of predicting weld sizes. Nied [4] developed an axi-symmetrical FE model which used elastic material behavior and Nishiguchi and Matsuyama [5] implemented elasto-plastic material behavior. Both designated welding simulation software and general simulations software have been used in published work. Sysweld [6] , jwrian [7] and sorpas [8] are FEM software designated for welding purposes and incorporates thermo-electro- mechanical modeling and modeling of the sheet contact conditions.
As the models achieved increased level of detail and accuracy, research also focused on comparison and veri- fication of physical experiments. Several studies have been made to verify the prediction of the FE simulations on weld sizes. Simulations were done by Tsai et al. [9] for mild steel, by Gupta and De [10] for HSLA steel, by Long and Khanna [11] for AISI 1010 steel and by Moshayedi and Sattari-Far [12] for 304L austenitic steel with good agreement to experiments. Nodeh et al. [13] verified result of mild steel with a 3D model with good agreement. Shen et al. [14] verified results of 3-sheet joints of combinations of DP600 and mild steel and reported that the model somewhat underestimated weld sizes in all interfaces. In addition, Afshari et al. [15] made comparative studies of 6061 aluminum alloy welds with good agreement between simulations and experiments.
Verification of simulations of UHSS is not as extensively investigated. Dancette et al. [16] showed good agreement between simulations and experiments for DP980 steel and Radakovic et al. [17] showed results of DP780 in a study which focused on failure modes of spot welds. However, no simulations of press-hardened or fully martensitic steels have been found in the literature.
The present paper includes verifications of FE simulations by comprehensive physical experiments. The ex- periments provide data on weld sizes and the occurrence of expulsion. The FE model used a new material data- base to describe the behavior of UHSS steels during welding. An investigation of the potential of a process planning tool based on FE simulations has been carried out.
2. Experimental Procedure
An extensive experimental procedure was carried out to find weld results for the analysed materials. Six materials were welded, ranging from advanced high strength steels as press hardened boron alloyed steel to lower strength steels. The materials’ mechanical properties and alloying content are presented in Table 1 and Table 2, respectively.
The welding was performed as 2-sheet overlap welds on sheets of dimensions 40 mm by 120 mm, with two welds on each sheet pair. The geometry and fixturing of the sheets are illustrated in Figure 1 and Figure 2.
Table 1. Materials used in experiments.
Figure 1. Sheet dimension and fixturing.
Figure 2. Welding fixture before welding.
Table 2. Alloying elements of materials.
The welding process can be divided into two time periods, weld time and hold time. The weld time refers to the period when a current is passed between the electrodes and the hold time refers to the period after the weld time when the electrode force are still applied to the sheets but no current is passed between them.
The weld parameters of the experiments, weld time, hold time and electrode force and weld currents, are pre- sented in Table 3. The minimum welding current was defined as the current which generated a weld diameter of approximately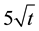 . The maximum welding current was defined as the current which generated two or three expulsion at the second weld location. An increment of 0.3 kA was used within the welding current range. Between each current step, the electrode tips were dressed. Each weld was repeated three times.
. The maximum welding current was defined as the current which generated two or three expulsion at the second weld location. An increment of 0.3 kA was used within the welding current range. Between each current step, the electrode tips were dressed. Each weld was repeated three times.
Welding was performed with a MFDC PSI6000 inverter and a PSG3050 transformer from Bosch Rexroth. An ISO 8521 B-type electrode of CuCrZr alloy was used.
Table 3. Process parameters of experimental welding.
The welded coupons were destructively tested using coach peel tests to measure the weld nugget by a digital calliper, as seen in Figure 3. The minimum and maximum diameters were measured to allow for elliptic nuggets and the arithmetic mean of the measurements was used for analysis. Expulsion was visually observed during experiments.
3. Finite Element Model
A coupled thermo-electro-metallographical-mechanical axi-symmetrical FE model was developed and computed using FE code SYSWELD. The model is built of axi-symmetric 2D solid elements, with degrees of freedom in displacement (radial and vertical), temperature and voltage. The metal sheets are composed of gradually increasing fineness of elements towards the symmetry line, as seen in Figure 4. The sheet elements are 0.1 mm in height for all sheet materials. The thermo-electrical and mechanical models, including governing equations, material models and boundary conditions are treated separately below.
3.1. Thermo-Electrical Model
Thermally, the RSW process can be described by the general electro-kinetic equation, as stated in (1), which adds a Joule heating term to the commonly used general heat equation.
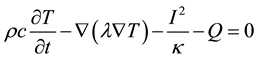 (1)
(1)
where temperature is designated T and time t. The first term includes the enthalpy of the system, c is the specific heat and ρ is the density. The second term includes the conductive heat component, where λ is the thermal conductivity. The third term includes the electro-thermal Joule heat, where I is the electrical current and κ is the electrical conductivity. The fourth term includes the internal heat generation, which is negligible due to pure Joule heating in the RSW process.
For the simulation material data input, the software Thermo Calc was used to determine the specific heat for all materials and microstructures based on thermodynamic equilibrium [18] . Thermo Calc calculated the specific heat from the alloying contents in the materials. Due to small variations between specific heat, a common model was used for all materials, shown in Figure 5. The density and electric conductivity were provided through the FE software and are shown in Figure 5.
The thermal conductivity data was generated using the material simulation software IDS [19] . The software uses thermal conductivity of the pure alloying elements, which are weighted against the thermal conductivity of pure iron. The thermal conductivity is shown in Figure 6.
The electrical boundary conditions are a description of the applied welding current and the physical boundaries of the sheet. No current is flowing at the water channel, at the symmetry line or at the metal sheet surface facing air, as indicated in Figure 4. The electric potential is applied between the electrodes, creating the Joule heating.
The metal surface-to-media heat exchanges are defined at the electrode-water interface, at the metal-air sheet interface and at the symmetry line, respectively, as lumped conductance according to (3) to (2) below.
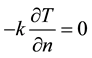 (2)
(2)
Figure 3. Coach-peel tested coupon.
Figure 4. Axi-symmetrical mesh of upper electrode and sheet.
Figure 5. Electrical and thermal material properties.
Figure 6. Heat conductivity.
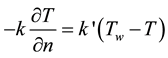 (3)
(3)
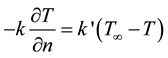 (4)
(4)
where n is the surface normal coordinate, 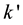 [W/(mK)] is a controlling conduction factor and Tw is the water temperature (20˚C) and T∞ is the ambient temperature (20˚C).
[W/(mK)] is a controlling conduction factor and Tw is the water temperature (20˚C) and T∞ is the ambient temperature (20˚C).
3.2. Mechanical Model
The solution of the thermo-electric model gives a temperature field which causes mechanical strains due to thermal expansion. The data for simulations is based on dilatometer experiments where the temperature of a test specimen was controlled and the volume changes were measured. The temperature was changed in order to gain all three microstructures; material as delivered, austenite and martensite. Results showed that the standard deviation between materials of the same microstructure is small. Thus, the thermal expansion coefficient is constant at all temperatures at 0.125e−4 K−1 for the material as delivered, 0.209e−4 K−1 for the austenite and 0.105e−4 K−1 for the martensite.
The strain components of the mechanical model can be decomposed as in (5).
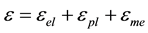 (5)
(5)
where 


A conventional method of defining a yield stress is by locating a specific divergence value between the two curves, i.e. a specific plastic strain magnitude. In the present work, the yield stress is defined as the stress where the plastic strain is 0.2%. As for the Young’s modulus, the yield stress was modeled using linear regression for each material, see Figure 8.
Regarding flow stress, optimized Hollomon curve stress-strain relations were optimized using MATLAB’s [20] optimization toolbox to match the results from the tensile tests for each material and temperature. Examples of resulting stress-strain curves for UHSS are shown in Figure 9.
The metallurgical transformation strains are defined according to Johnson-Mehl-Avrami’s transformation kinetics model. The martensitic transformation temperatures are defined according to Table 4 and found through dilatometer tests.
The electrode force is applied at the top nodes of the top electrode and a mechanical boundary condition is imposed on the bottom nodes of the bottom electrode by locking all displacement components. Furthermore, the radial displacements are locked along the symmetry line.
Table 4. Martensitic transformation temperature.
Figure 7. Elastic material properties.
Figure 8. Yield strength.
Figure 9. Plastic behaviour of UHSS materials at elevated temperatures.
After the complete welding cycle is finished, the electrodes are removed from the sheets and a new set of boundary conditions are applied to the model. Firstly, the radiation component of the sheet surface heat transfer is neglected over the entire sheet. Secondly, the electrical contact condition is removed. Thirdly, both electrodes are set to a vertical displacement of 3 mm away from the sheets.
In post-processing, the weld nugget is defined as the material which has reached a peak temperature above the solidus temperature, defined as in Table 5 according to Thermo Calc simulations.
It is also of interest to predict the expulsion limit through the FE model. Shen et al. [21] introduced the factor η, the ratio between the weld nugget radius (Rn) and contact radius between the sheets (Rc) in order to predict expulsion. A requirement for expulsion was formulated as shown in (6).

In the FE post-processing, expulsion was reached if the molten zone was in contact with the air gap between the sheets. The present paper evaluated the capability of the η-factor method on a broad sheet material range.
4. Results
The experimental welding results were recorded between a low current which gave a nugget diameter of approximately 
Table 5. Solidus temperatures
coupon with steps of 0.3 kA between. Due to the high weldability of the stack-ups, an extensive amount of data was collected for verification.
Due to the different alloying elements and microstructures of the materials, the coach-peel tests resulted in different failure modes. The boron steel coach-peel tests resulted in interfacial failures whereas the other steels gave pullout plugs.
Expulsion was identified and recorded during the experimental welding. The expulsion occurrence can be seen as discrete probability distributions for both the first and second weld location. The expected value of the expulsion limit, Ilim, can be calculated as in (7).

where Pexp denotes the proportion of expulsion welds at each weld current. When two of three welds at the second location showed expulsions, the weld lobe was ended.
Simulation Results and Discussion
Each experimental test was compared with a FE simulation using the simulation method described above. The recorded results of the simulation were the weld nugget diameter and the possible occurrence of expulsion in the simulation model.
During welding of the second weld, a proportion of the current will pass through the first weld due to the high conductance at the already bonded material. Thus, the current passing through the faying surface at the second weld location will be reduced compared to the nominal current, resulting in lower heat generation by Joule heating. Consequently, the second weld on the coupon showed a somewhat lower weld nugget size than the first weld in the experiments.
In general, the difference in size between the first and second weld on the coupons with identical current was on average 0.38 mm. This difference is depends on the distance between the weld of 40 mm. The simulation does not take shunting into account and is thus more comparable to the first weld. However, the second weld is of higher interest for process planning since shunting currents occur in almost all industrial welding. Thus, it is of interest to see the accuracy of simulations compared to experiments for both welds.
The results show a good agreement between weld sizes from simulation and physical welding. The agreement is illustrated in Figure 10 and quantified by mean absolute errors in Table 6.
The mean absolute error between the weld size diameter of the FE model and the experiments is 0.53 mm for all welds. The first weld is more accurately modeled with a mean absolute error of 0.42 mm compared to 0.64 mm for the second weld. The better agreement of the first weld is expected due to the similar boundary conditions with regard to shunting currents. The results indicate that shunting currents are significant to model in order to improve accuracy of simulations.
It is of interest to compare the mean absolute error of the FE model to the standard deviation of weld size results in physical testing, since variations in experimental test results occur. Previous research has shown the standard deviation of weld sizes in experiments to be approximately 0.3 mm [22] . Thus, the error of the FE model is 76% larger than the variation of the experiment results themselves. However, for specific materials, the mean absolute error is as low as 0.22 mm (boron steel), 0.38 mm (martensitic steel) and 0.34 mm (rephosphorized steel), which is comparable to the variations in experimental outcome.
Figure 10. Resultsfromsimulationsandphysicaltesting of weld nugget size. Squaresdenotethe 1st physical weld andtrianglesdenotethe 2nd physical weld.
Table 6. Mean absolute error between experimental and simulation results of weld sizes.
The proportion of expulsions in the experiments gave an expected value of the expulsion limit. Also, the simulations gave an expulsion limit based on the weld zones contact with the air gap, as described above.
Again, the shunting effects during the second welding results in lower weld current and will also affect the expulsion limit. The results showed that the average difference of expected expulsion limit between the first and second weld location is 0.33 kA. Again, this relation is proportional to the shunting distance between the welds of 40 mm.
The agreement between expulsion limits in experiments and simulations is illustrated in Figure 11. The results show that the expulsion limit is generally underestimated in simulations and that the mean absolute error between expulsion limit between the simulations and the physical testing is 1.10 kA. The mean absolute error of the first weld location is 1.04 kA and 1.16 kA for the second weld location. Thus, it can be concluded that the expulsion limit better capture the expulsion of the first weld location, which is expected since no shunting effects are modeled in the simulations.
As with weld sizes, expulsion limits has variations in physical testing. By considering the expulsion occur- rence as a discrete probability distribution, as with the expected value, the standard deviation of expulsion limit can be measured. The average standard deviation of expulsion limits is 0.34 kA and 0.08 kA for the first and second weld location, respectively. The standard deviation of all welds is 0.21 kA.
Figure 11. Results from simulation and physical testing of expulsion limit.
The mean absolute error of the expulsion limit in simulation compared to experiments is higher than the standard deviation of the expulsion limit in physical testing. For a more detailed study of expulsion limits, smaller current steps than 0.3 kA should be used for analysis, which would give a higher resolution of results.
5. Conclusions
The major points of the present paper can be summarized as follows.
Resistance spot weld experiments of six steel types, including UHSS, have been performed in a semi-indus- trial environment using weld equipment used in automotive production and assessed using coach-peel tests of weld sizes and expulsion occurrence.
Material data for FE simulations of the RSW process have been generated from experiment tests of material specimens, material simulations and literature sources.
An electro-thermo-mechanical FE model has been developed based physical phenomena in resistance spot welding.
The simulations showed an agreement with the experimental results with a mean absolute error of weld sizes of 0.68 mm with all welds taken into account Comparably, variations of weld sizes in apparently identical physical testing is 0.30 mm.
The simulations showed an agreement with the experimental results with a mean absolute error of the expulsion limit of 1.10 kA when all welds were taken into account. Comparably, variations of expulsion limit in physical testing are 0.21 kA.
In conclusion, in the present paper weld sizes and occurrence of expulsion have been quantified for a wide range of steel types of different alloying content and heat treatment. The study shows the potential and limitations of the generated temperature-dependent material model and the FE model. The results can be used for implementation of FE simulations in process planning of RSW in modern manufacturing. The results show that the accuracy between physical experiments and simulations is comparable to the variations of weld output in industrial welding. Thus, the prediction accuracy of simulations is useful for engineers for process planning as the possible error is within magnitude of the process variations.
For further analysis of the inaccuracy of the simulations, the experimental methods should be extended with more detailed measurement of temperature history and stress-states in order to identify possible sources of errors in the FE model and material data. Although the accuracy of the simulations varies among materials, it should be noted that the common material model is fairly accurate. For further broadness of the results, it is of interest to extend the material model to other low-weight materials such as aluminum.
Due to the limitations of the FE software, the present study excluded effects of shunting currents in the simulations. For further accuracy of simulations for process planning, effects of shunt current should be included in the model to emulate industrial welding more accurately. Furthermore, a more advanced model of the steel, particularly its behavior in the molten state and the pressure state within the weld would likely increase the accuracy of expulsion prediction and increase the understanding of the causes of expulsion. Finally, as highlighted above, in industrial manufacturing the RSW inherits variations in both weld sizes and expulsion. Such variations are not treated in the simulations, which use nominal input data. To increase the capability of the simulations, a sensitivity analysis of the FE model and material data should be performed.
Acknowledgements
This work was supported by the Swedish Governmental Agency for Innovation Systems (VINNOVA) [grant number 2009-01585] through the project Spot Light. The authors wish to thank the members of the steering committee of Spot Light for many contributions to the present work. The material testing and simulation was conducted by Johannes Gårdstam, Sven Haglund and Greta Lindwall at Swerea KIMAB.
References
- Weber, G., Thommes, H., Gaul, H., Hahn, O. and Rethmeier, M. (2010) Resistance Spot Welding and Weldbonding of Advanced High Strength Steels. Materialwissenschaft und Werkstofftechnik, 41, 931-939. http://dx.doi.org/10.1002/mawe.201000687
- Archer, G. (1960) Calculations for Temperature Response in Spot Welds. Welding Journal, 39, 327-s-330-s.
- Greenwood, J. (1961) Tempera in Spot Welding. British Welding Journal, 8, 316-322.
- Nied, H. (1984) The Finite Element Modelling of the Resistance Spot Welding Process. Welding Journal, 63, 123s- 132s.
- Nishiguchi, K. and Matsuyama, K. (1987) Influence of Current Wave Form on Nugget Formation Phenomena When Spot Welding Thin Steel Sheet. Welding in the World, 25, 222-244.
- Feulvarch, E., Rogeon, P., Carr, P., Robin, V., Sibilia, G. and Bergheau, J. (2006) Resistance Spot Welding Process: Experimental and Numerical Modeling of the Weld Growth Mechanisms with Consideration of Contact Conditions. Numerical Heat Transfer Part A: Applications, 49, 345-367. http://dx.doi.org/10.1080/10407780500359760
- Murakawa, H., Zhang, J., Fujii, K., Wang, J. and Ryudo, M. (2000) FEM Simulation of Spot Welding Process. Transactions of JWRI, 29, 73-80.
- Zhang, W. (2003) Design and Implementation of Software for Resistance Welding Process Simulations. SAE Technical Papers 2003-01-0978. http://dx.doi.org/10.4271/2003-01-0978
- Tsai, C.L., Dai, W.L., Dickinson, D.W. and Papritan, J.C. (1989) Analysis and Development of a Real-Time Control Methodology in Resistance Spot-Welding. Welding Journal, 70, 339s-351s.
- Gupta, O. and De, A. (1998) An Improved Numerical Modeling for Resistance Spot Welding Process and Its Experi- mental Verification. Journal of Manufacturing Science and Engineering, Transactions of the ASME, 120, 246-251. http://dx.doi.org/10.1115/1.2830120
- Long, X. and Khanna, S.K. (2003) Numerical Simulation of Residual Stresses in a Spot Welded Joint. Journal of Engineering Materials and Technology, 125, 222-226. http://dx.doi.org/10.1115/1.1543968
- Moshayedi, H. and Sattari-Far, I. (2012) Numerical and Experimental Study of Nugget Size Growth in Resistance Spot Welding of Austenitic Stainless Steels. Journal of Materials Processing Technology, 212, 347-354. http://dx.doi.org/10.1016/j.jmatprotec.2011.09.004
- Nodeh, I.R., Serajzadeh, S. and Kokabi, A.H. (2008) Simulation of Welding Residual Stresses in Resistance Spot Welding, FE Modeling and X-Ray Verification. Journal of Materials Processing Technology, 205, 60-69. http://dx.doi.org/10.1016/j.jmatprotec.2007.11.104
- Shen, J., Zhang, Y., Lai, X. and Wang, P.C. (2011) Modeling of Resistance Spot Welding of Multiple Stacks of Steel Sheets. Materials and Design, 32, 550-560. http://dx.doi.org/10.1016/j.matdes.2010.08.023
- Afshari, D., Sedighi, M., Karimi, M.R. and Barsoum, Z. (2013) On Residual Stresses in Resistance Spot-Welded Aluminum Alloy 6061-T6: Experimental and Numerical Analysis. Journal of Materials Engineering and Performance, 22, 3612-3619. http://dx.doi.org/10.1007/s11665-013-0657-1
- Dancette, S., Massardier-Jourdan, V., Fabrègue, D., Merlin, J., Dupuy, T. and Bouzekri, M. (2011) HAZ Microstructures and Local Mechanical Properties of High Strength Steels Resistance Spot Welds. ISIJ International, 51, 99-107. http://dx.doi.org/10.2355/isijinternational.51.99
- Radakovic, D.J. and Tumuluru, M. (2008) Predicting Resistance Spot Weld Failure Modes in Shear Tension Tests of Advanced High-Strength Automotive Steels. Welding Journal (Miami, Florida), 87, 96-105.
- (2008) Thermo-Calc for Windows Version 5 User’s Guide.
- Miettinen, J., Louhenkilpi, S., Kytönen, H. and Laine, J. (2010) IDS: Thermodynamic-Kinetic-Empirical Tool for Modeling of Solidification, Microstructure and Material Properties. Mathematics and Computers in Simulation, 80, 1536-1550. http://dx.doi.org/10.1016/j.matcom.2009.11.002
- (2007) MATLAB Documentation.
- Shen, J., Zhang, Y. and Lai, X. (2010) Influence of Initial Gap on Weld Expulsion in Resistance Spot Welding of Dual Phase Steel. Science and Technology of Welding and Joining, 15, 386-392. http://dx.doi.org/10.1179/136217110X12693513264213
- Andersson, O. and Melander, A. (2011) Statistical Analysis of Variations in Resistance Spot Weld Nugget Sizes. IIW Annual Assembly, Chennai.













