Modeling and Numerical Simulation of Material Science
Vol.4 No.1(2014), Article ID:41682,6 pages DOI:10.4236/mnsms.2014.41003
Model for a UV Laser Based Local Polymer Surface Halogenation Process Using a Gaseous Precursor
BIAS—Bremer Institut für Angewandte Strahltechnik GmbH, Bremen, Germany
Email: kibben@bias.de
Copyright © 2014 Simon Kibben. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Simon Kibben. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 19, 2013; revised December 19, 2013; accepted December 27, 2013
Keywords:Local Surface Halogenation; Polymer Modification; UV-Laser-Based Surface Modification
ABSTRACT
An analytical model describing the physical relations of a UV-based process for halogenation of polymeric surfaces is presented. The process allows, depending on the parameters, a local halogenation with sharp edges at the interfaces to areas where no halogenation is desired. This is achieved via a nonreactive halogen-containing gaseous precursor and a UV source providing photons which dissociate the precursor photolytically. Thus, only where the UV photons affect the precursor, halogens are generated and the polymer is being halogenated.
1. Introduction
Halogenation of polymeric surfaces is a common tool to enhance the properties for adherence and inhibition of carbohydrate diffusion [1]. In the reaction, hydrogen is replaced by halogens. In case of fluorine, this is achieved inside a reactor where the polymer is placed and the halogen is introduced in the gas phase. Usually the halogen reacts with the whole surface of the polymer. A second well-established process is the plasma halogenation, where a non-reactive gas containing the halogen is dissociated via a plasma [2]. In cases, where e.g. a halogenation of a polymeric surface should take place only in certain areas, this is normally achieved via a masking of the areas which must not be halogenated. The plasma halogenation processes also allow a local halogenation as demonstrated by [3]. There the plasma is not intended to modify the surface but to remove it selectively with a gasussian-like removal profile.
When a non-reactive UV-dissociable precursor is used, no masking is necessary. With the right choice of parameters, a local halogenation can be achieved. For this, a laser with a wavelength (photon energy) being able to dissociate the precursor has to be chosen. In order to dissociate the precursor only in areas, where a halogenation is desired, a shadow mask has to be inserted in the beam path.
The here discussed process is comparable to a process introduced by [4]. In their experiments, two UV sources (Xe2* excimer lamp, ArF excimer laser) were used at the same time to fluorinate a polymeric surface incorporating a nonreactive precursor (CF4 gas). The radiation of the Xe2* excimer lamp dissociated the precursor, the ArF excimer laser activated chemical bonds of the polymer. Later it was shown, that the process also works with one UV source (Xe2* excimer lamp) [5]. A comparable process also was achieved utilizing a different precursor (1,2,3,5-Tetrafluorobenzene) and a KrF excimer laser was introduced [6].
2. Process Fundamentals
The general process modeled here is intended to forecast the efficiency of a UV-laser based halogenation process. The setup consists of a pulsed UV laser (i.e. KrF excimer laser). The beam of the laser is being expanded using four cylindrical lenses and a rectangular aperture is put in the beam to cut off the boundary areas of the beam with an inhomogeneous energy distribution. The beam then is directed into a vacuum chamber through a CaF2 window. Inside the chamber, the polymer sample is placed in a defined distance to the window. The chamber can be evacuated down to 1×10−2 mbar. The precursor is put into the chamber via a needle valve to precisely control the pressure of the precursor.
The modeled part of the process is the UV-induced reaction inside the vacuum chamber. The general process is depicted in Figure 1. As an example for the halogenation process, a surface fluorination of a polymer is shown in the depiction. Four different steps are marked in the depiction, although the process is divided into three parts in the following.
The first one is the photo dissociation of the precursor molecule forming a radical (or an ion depending on the chemical polarity of the precursor molecule; from here on, it will be named a radical). The second step shows the movement of the radical towards the surface. In the third step, the radical has reached the surface and has a certain probability to replace a hydrogen atom of the polymer chain. The fourth step depicted shows the process of radical bonding to a precursor molecule. This limits the efficiency of the process and the maximal distance between the radical and the polymer surface, thus the probability of a radical of reaching the surface decreases with increasing distance to the surface. The second and fourth steps are treated together as one process part.
In the following chapter, the three main parts of the model to describe this process will be examined.
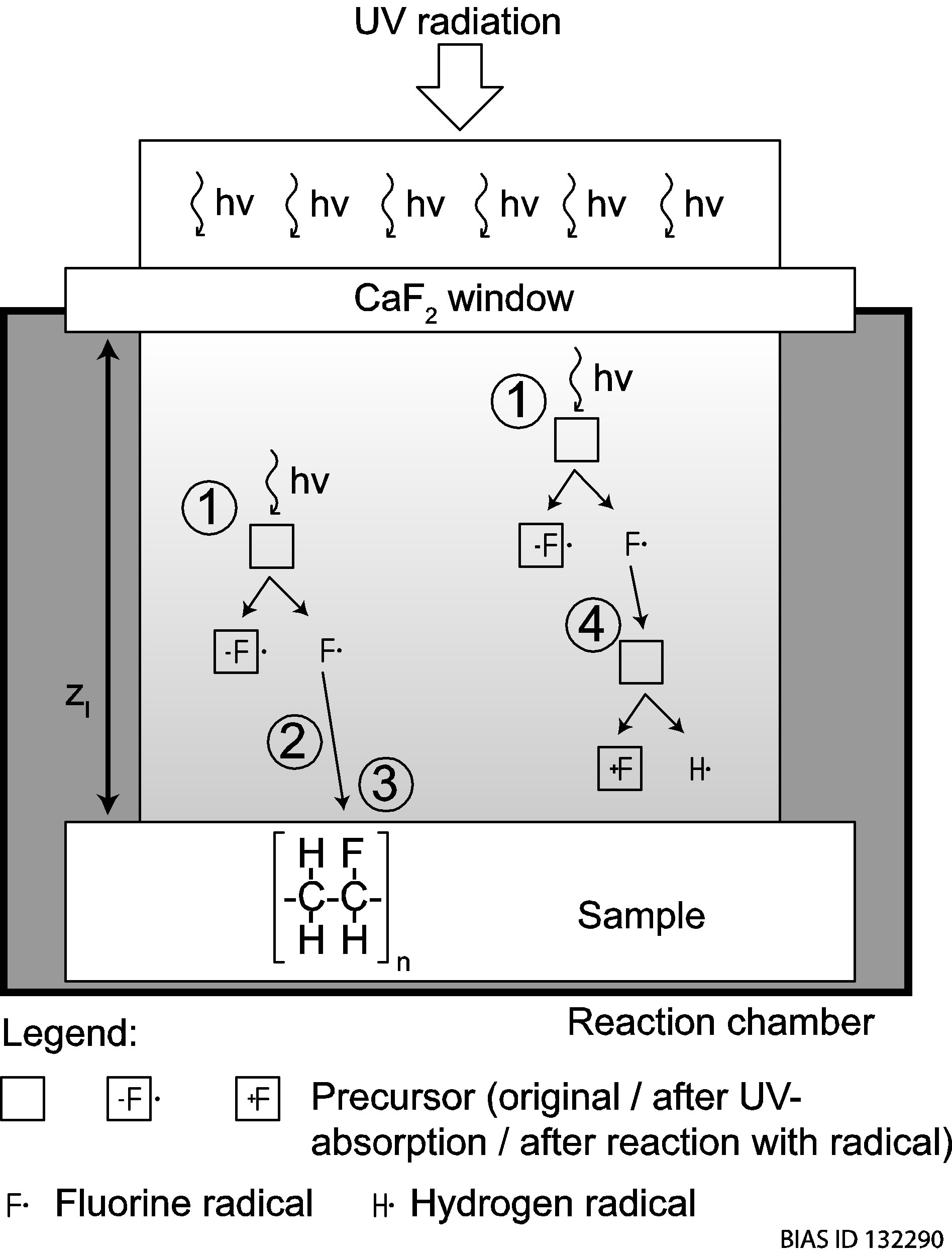
Figure 1. Assumed set-up and modeled processes, depicted for the case of fluorination.
3. Description of the Model
3.1. Photodissociation
The UV photodissociation of the precursor only depends on the cross-section of the precursor molecule. In order to photolytically dissociate many precursor molecules, one has to look at the cross section in dependence of the wavelength and select a wavelength, where the cross section is high. This is the case when the photon energy meets the bond-dissociation energy of the radical and the precursor. In the modeling of the photodissociation process, a single photon photodissociation is assumed. For twoor more-photon absorption, Equations (1) and (2) have to be adopted, as for example described in [7-9].
The fluence can be described by the Beer-Lambert law. The fluence inside the precursor in a distance  from the entrance window is described by
from the entrance window is described by
 . (1)
. (1)
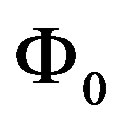 is the incoming fluence of the UV beam at the interface of the window into the reactor. From here on the UV photon flux will be referred to as the fluence (Joules per meter squared), regardless if the laser source is a pulsed one or emits a continuous wave.
is the incoming fluence of the UV beam at the interface of the window into the reactor. From here on the UV photon flux will be referred to as the fluence (Joules per meter squared), regardless if the laser source is a pulsed one or emits a continuous wave.  is the absorption coefficient of the precursor. It depends on the precursor density
is the absorption coefficient of the precursor. It depends on the precursor density 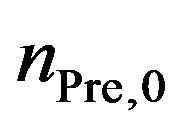 and the cross section for the UV wavelength
and the cross section for the UV wavelength ,
,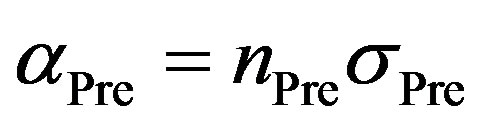 . The interface of the polymer and the precursor in z-direction is at
. The interface of the polymer and the precursor in z-direction is at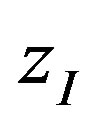 . Inside the polymer, the fluence in dependence of
. Inside the polymer, the fluence in dependence of 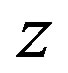 is calculated to
is calculated to
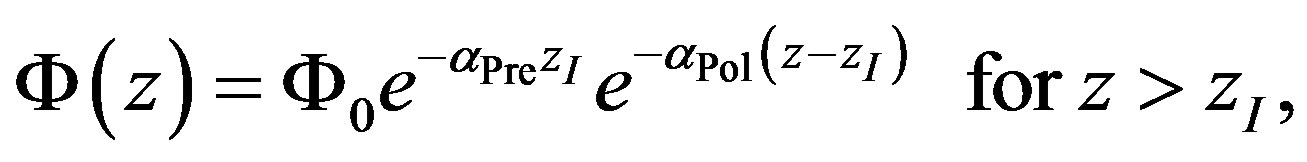 (2)
(2)
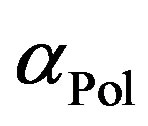 is the absorption coefficient of the polymer.
is the absorption coefficient of the polymer.
To calculate the radical density 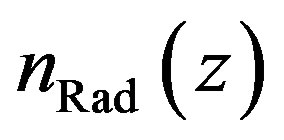 generated at the height
generated at the height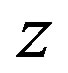 , the density of absorbed photons at that height has to be known. The density of absorbed photons can be calculated via the photons per meter squared
, the density of absorbed photons at that height has to be known. The density of absorbed photons can be calculated via the photons per meter squared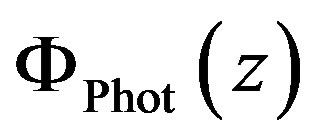 , which is proportional to the fluence
, which is proportional to the fluence
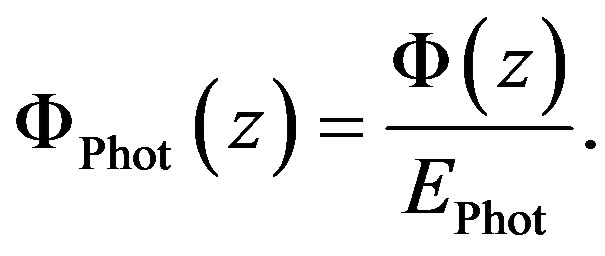 (3)
(3)
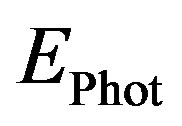 is the photon energy in Joules.
is the photon energy in Joules. 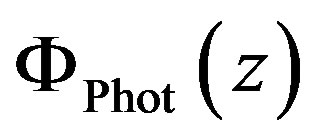 will be referred to as the photon fluence. The derivative with respect to
will be referred to as the photon fluence. The derivative with respect to 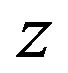 of the photon fluence is the density of absorbed photons at the height
of the photon fluence is the density of absorbed photons at the height 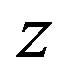
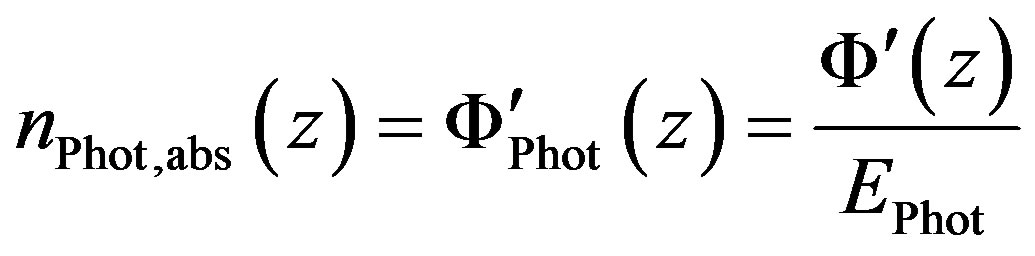 (4)
(4)
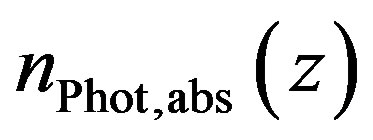 is negative in the case of absorption, as the photon density decreases.
is negative in the case of absorption, as the photon density decreases.
In order to calculate the number of photons absorbed in the distance from  to
to , one has to integrate the density of absorbed photons.
, one has to integrate the density of absorbed photons.
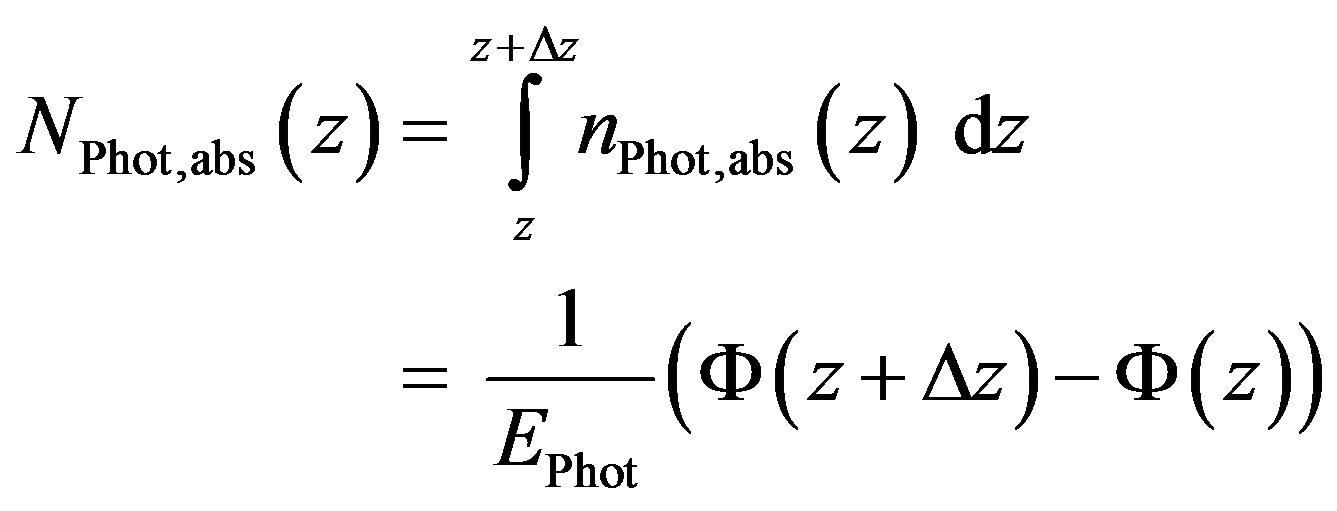 (5)
(5)
The relation between generated radicals 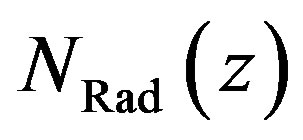 and absorbed photons
and absorbed photons 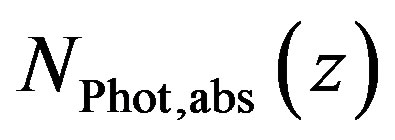 depends on the photolytic reaction, which is defined by the precursor molecule and the energy of the UV photons. This is also true for the radical density
depends on the photolytic reaction, which is defined by the precursor molecule and the energy of the UV photons. This is also true for the radical density 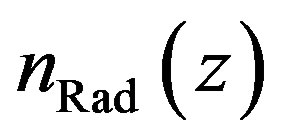 and the density of absorbed photons
and the density of absorbed photons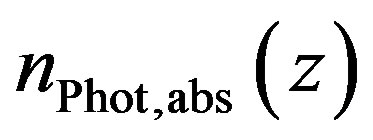 . In a simple case, each absorbed photon dissociates a precursor molecule generating a radical (or an ion, depending on the chemical polarity of the precursor molecule). In some cases where the photodissociation is not done by a single photon, the amount of generated radicals is not proportional to the photon flux [10]. On continuous wave (cw) sources, the flux does not change over time. For pulsed sources, the flux changes depending on the pulse shape. In the cases where two or more photons have to be absorbed by one and the same precursor molecule, two cases can occur. In the classical two-photon-absorption, two photons have to be absorbed at the same time. In the second case, the precursor molecule stays in a metastable excited state for a while after absorption of the first photon. In the latter case, the second photon needs to be absorbed while the molecule is in the excited state. Sometimes, both ways of photodissociation can occur [8]. The correlation between absorbed photons then strongly depends on the photon flux. This has extensively been described in literature [11].
. In a simple case, each absorbed photon dissociates a precursor molecule generating a radical (or an ion, depending on the chemical polarity of the precursor molecule). In some cases where the photodissociation is not done by a single photon, the amount of generated radicals is not proportional to the photon flux [10]. On continuous wave (cw) sources, the flux does not change over time. For pulsed sources, the flux changes depending on the pulse shape. In the cases where two or more photons have to be absorbed by one and the same precursor molecule, two cases can occur. In the classical two-photon-absorption, two photons have to be absorbed at the same time. In the second case, the precursor molecule stays in a metastable excited state for a while after absorption of the first photon. In the latter case, the second photon needs to be absorbed while the molecule is in the excited state. Sometimes, both ways of photodissociation can occur [8]. The correlation between absorbed photons then strongly depends on the photon flux. This has extensively been described in literature [11].
The radical density can be generically described as
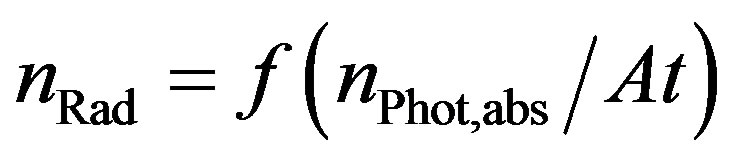 (6)
(6)
Here  is the UV laser beam cross section and
is the UV laser beam cross section and 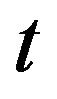 is the time constant in which the photons pass through the cross section. The function itself depends on the photolytical process and has to be derived individually for each precursor molecule in order to calculate the radical density.
is the time constant in which the photons pass through the cross section. The function itself depends on the photolytical process and has to be derived individually for each precursor molecule in order to calculate the radical density.
In general, the highest radical density is generated where the fluence is the highest. Taking the described setup into account, the highest fluence is at the interface of the window to the precursor.
A high number of generated radicals is not enough for a high degree of halogenation. Also the distance between the radicals to the surface strongly affects the degree of fluorination. The radicals do have a limited lifetime, which sets their average travelling distance.
3.2. Path of the Radical
As radicals usually are highly reactive, it is assumed that the halogen radical will react with the first collision partner. For low irradiation doses, the radical density is much smaller than the precursor density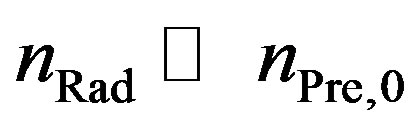 . The radical density usually is a few orders of magnitudes smaller than the precursor density. Thus it is assumed that collisions between two radicals will take place only very rarely. In the model, this process is neglected. Only the two main processes are investigated; the first one, where the radical collides with a precursor molecule, and thus is no longer available for a reaction with the polymer, and the second one, where the radical collides with the polymer.
. The radical density usually is a few orders of magnitudes smaller than the precursor density. Thus it is assumed that collisions between two radicals will take place only very rarely. In the model, this process is neglected. Only the two main processes are investigated; the first one, where the radical collides with a precursor molecule, and thus is no longer available for a reaction with the polymer, and the second one, where the radical collides with the polymer.
In order to calculate the number of halogens per unit area reaching the polymer surface, the probability of a radical to reach the surface in dependence of the distance and the precursor density  is calculated. First the probability of the radical to travel a certain distance
is calculated. First the probability of the radical to travel a certain distance 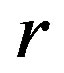 is calculated. The probability depends on the precursor density
is calculated. The probability depends on the precursor density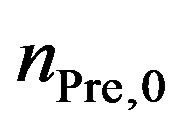 , the diameter of the precursor molecule
, the diameter of the precursor molecule  and on the diameter of the radical
and on the diameter of the radical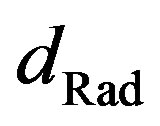 . A distance, which
. A distance, which 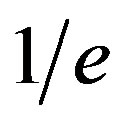 radicals will reach, is called the mean free path. It is defined as
radicals will reach, is called the mean free path. It is defined as
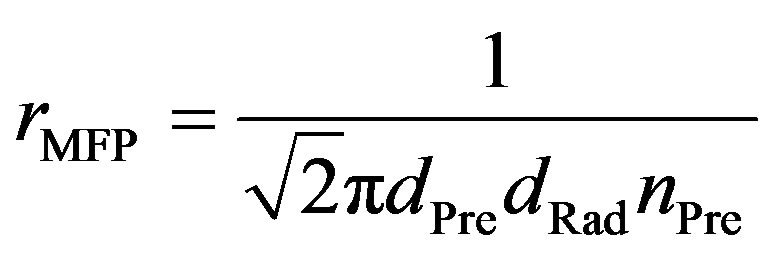 . (7)
. (7)
So the probability of a radical to reach a distance  is
is
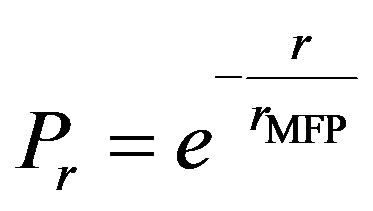 . (8)
. (8)
The radical can go into any direction from its origin. The probability to go into a certain direction is zero and cannot be used for further calculations, but a range of directions is the basis for the calculation of the probability of a radical to reach the polymer surface.
For calculating the probability of a radical to go into a range of directions, a conceptual model is used. All directions are represented by the surface of a sphere with its center point at the origin of the radical. The probability of the radical to go into a range of directions (pointing at a certain area of the sphere) is the surface of that area divided by the surface area of the whole sphere. In our case, where the probability of a radical to reach a surface (a layer) has to be calculated, the area of the sphere can be divided into many spherical segments. The spherical segments are parallel to the surface. The probability of the radical to pass through a certain segment is the surface area of the segment divided by the surface area of the sphere. The segments are defined by an angle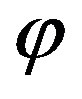 , which is the angle between the surface normal and the direction of the radical and a second angle
, which is the angle between the surface normal and the direction of the radical and a second angle  defining the range. The angular range is then from
defining the range. The angular range is then from 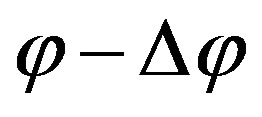 to
to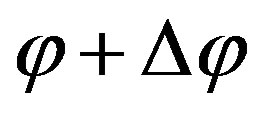 . With an angle
. With an angle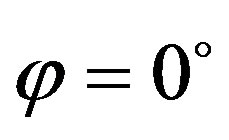 , the radical takes the shortest way possible, with an angle of
, the radical takes the shortest way possible, with an angle of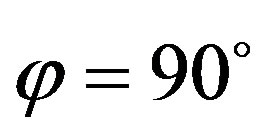 , the radical travels parallel to the surface and with angles
, the radical travels parallel to the surface and with angles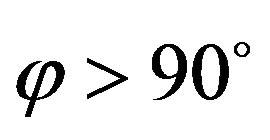 , the radical moves away from the surface. For the model consideration, the direction in x and y is not relevant (z is the surface normal). So the probability to reach the surface only depends on the height
, the radical moves away from the surface. For the model consideration, the direction in x and y is not relevant (z is the surface normal). So the probability to reach the surface only depends on the height  of the origin or the radical and the angle
of the origin or the radical and the angle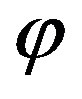 . Both defines the length of the path the radical has to overcome without a collision.
. Both defines the length of the path the radical has to overcome without a collision.
To calculate the overall probability of a radical with its origin in a distance of 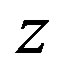 to the polymer surface travelling in a certain range of directions
to the polymer surface travelling in a certain range of directions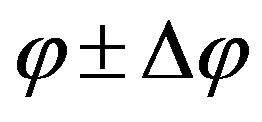 , the single probability of going into that range of directions and the probability to overcome the distance r without a collision has to be calculated. First, the probability to go into the direction
, the single probability of going into that range of directions and the probability to overcome the distance r without a collision has to be calculated. First, the probability to go into the direction  is examined.
is examined.
The probability 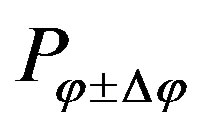 of the radical to go into the direction of a certain spherical segment is
of the radical to go into the direction of a certain spherical segment is
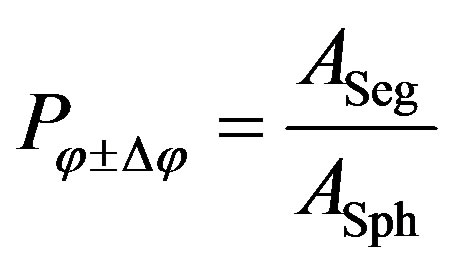 . (9)
. (9)
The surface area of a spherical segment 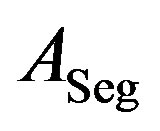 is calculated via its radius and the height of the segment,
is calculated via its radius and the height of the segment, . This leads to
. This leads to
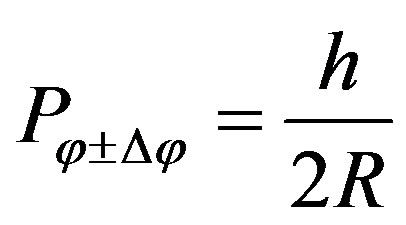 (10)
(10)
The radius can be assumed as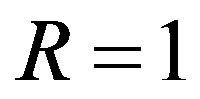 , the height h can be calculated via the two angles,
, the height h can be calculated via the two angles,
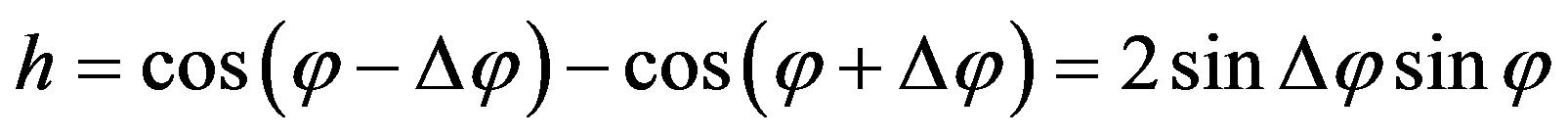 . (11)
. (11)
The probability 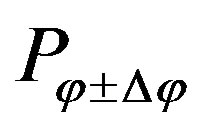 has to be multiplied with the probability
has to be multiplied with the probability 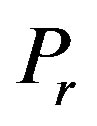 to reach a certain distance
to reach a certain distance 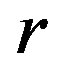 with
with 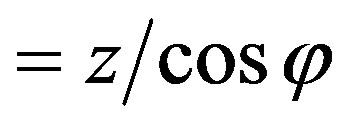 .
.
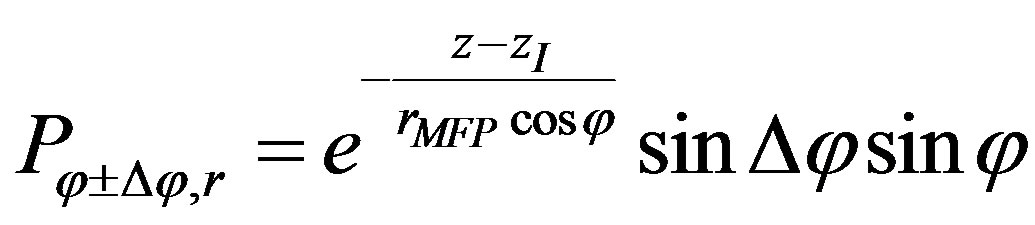 . (12)
. (12)
In Equation (12), the probability of a radical to go into a certain direction 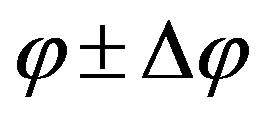 and reaching the surface is presented. The probability strongly depends on
and reaching the surface is presented. The probability strongly depends on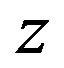 . Note that we have to use the distance between the interface of the polymer to the precursor and the radical, which is
. Note that we have to use the distance between the interface of the polymer to the precursor and the radical, which is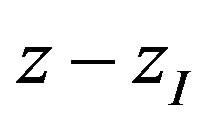 . The general probability
. The general probability 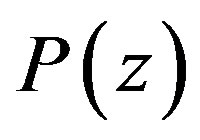 to reach the surface, independently of the direction is achieved via summing up the single probabilities for each direction.
to reach the surface, independently of the direction is achieved via summing up the single probabilities for each direction.
 (13)
(13)
The smaller 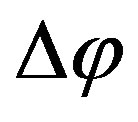 is chosen, the more precise the result will be. With this formula, it is possible to calculate the probability to reach the surface of a radical with the origin at a height
is chosen, the more precise the result will be. With this formula, it is possible to calculate the probability to reach the surface of a radical with the origin at a height . To calculate the number of radicals reaching the surface from that height, the probability has to be multiplied with the generated radical density
. To calculate the number of radicals reaching the surface from that height, the probability has to be multiplied with the generated radical density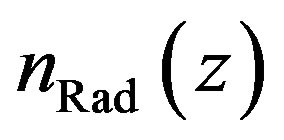 , the cross section of the laser beam
, the cross section of the laser beam 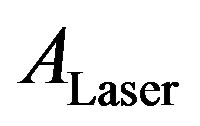 and the height interval
and the height interval . The number of radicals reaching the polymer surface then is
. The number of radicals reaching the polymer surface then is
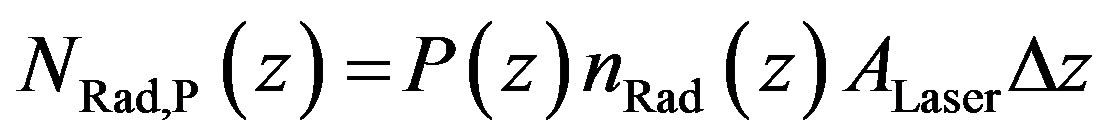 (14)
(14)
To obtain the total number of radicals reaching the polymer surface from a volume between z and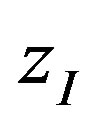 ,
, 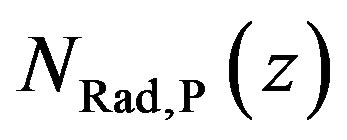 has to be summed up.
has to be summed up.
 (15)
(15)
Note that the number is with respect to the cross section of the laser beam.
3.3. Reaction of the Radical with the Polymer Surface
With Equation (15), the number of radicals reaching the polymer surface can be calculated. In order to estimate the reaction speed, one has to look at several factors. In general, the reaction speed depends on the concentration of both reactants, in this case the concentration of the halogen and the hydrogen. The activation energy and the absolute temperature also play a major role in estimating the reaction speed. The activation energy itself depends on the ongoing reaction, which halogen radical is supposed to replace the hydrogen in which polymer. As the concentration of the hydrogen gets lower with an ongoing reaction, also the reaction speed will get lower. With the assumption, that the halogen radical concentration/density is independently of time, the concentration of the hydrogen atoms in the top layer of the polymer 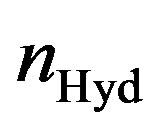 can be described by the following equation:
can be described by the following equation:
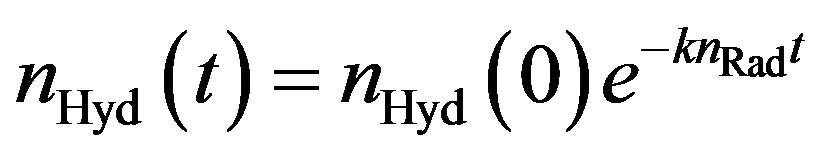 (16)
(16)
with  as the reaction constant. The reaction constant
as the reaction constant. The reaction constant 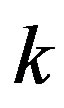 includes the activation energy
includes the activation energy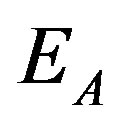 , the absolute temperature
, the absolute temperature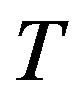 , the collision cross section of both reaction partners
, the collision cross section of both reaction partners , their reduced mass
, their reduced mass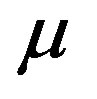 , the Boltzmann constant
, the Boltzmann constant 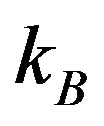 and the Avogadro constant
and the Avogadro constant  which all are integrated in Arrhenius’ equation.
which all are integrated in Arrhenius’ equation.
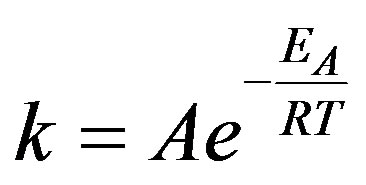 (17)
(17)
with  The equation cannot directly be applied to the reaction, as it only gives good results for reactions of ideal gases. The case of real molecules may be integrated via the insertion of the so called steric factor
The equation cannot directly be applied to the reaction, as it only gives good results for reactions of ideal gases. The case of real molecules may be integrated via the insertion of the so called steric factor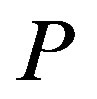 . This factor takes the deviation of the molecules shape from the ideal spherical shape into account. Usually the factor is measured by comparing the theory with the experiment.
. This factor takes the deviation of the molecules shape from the ideal spherical shape into account. Usually the factor is measured by comparing the theory with the experiment.
As the concentration of one reaction partner will get lower with the time, the fluorine content of the surface will rise more slowly with ongoing time. The correlation can be expressed by the following equation:
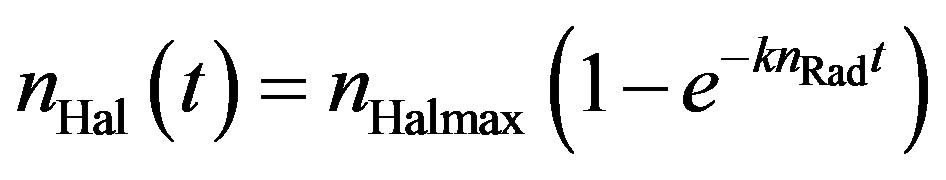 (18)
(18)
The UV radiation also plays an important role in the reaction, which cannot be neglected. Depending on the polymer, the radiation is absorbed and activates certain bonds of the polymer. This lowers the activation energy of the reaction of the radical with the hydrogen at these bonds. Hence, the reaction of the halogen is more probable compared to unactivated bonds. To be accurate, this has to be taken into account when the reaction of the radicals with the polymer is being described.
4. Results of the Model
The model was used to calculate the total number of radicals reaching the surface 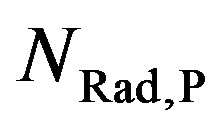 over the precursor density
over the precursor density  and
and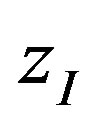 . The fluence was set to
. The fluence was set to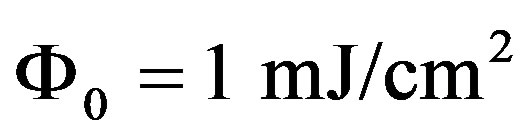 . The cross section was assumed to be
. The cross section was assumed to be . The multiplied diameters of precursor and the radical was assumed to be
. The multiplied diameters of precursor and the radical was assumed to be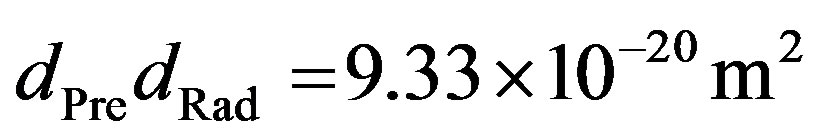 . For the calculation with equation (15),
. For the calculation with equation (15),  was chosen to be
was chosen to be .
.
The result is depicted in Figure 2. It is clearly noticeable that for a certain pressure, a distance 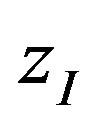 can be chosen to achieve a high amount of halogen radicals reaching the surface
can be chosen to achieve a high amount of halogen radicals reaching the surface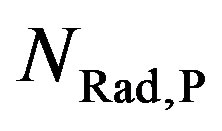 .
.
Depending on the pressure (or particle density), the mean free path was calculated via Equation (7). The results are shown in Figure 3. The mean free path describes a quantity closely related to the “range” of the radicals. Thus, the sharpness of the edges between fluorinated and non-fluorinated areas depends on the quantity. The smaller the mean free path is, the sharper the edges

Figure 2. Results of the model calculation.
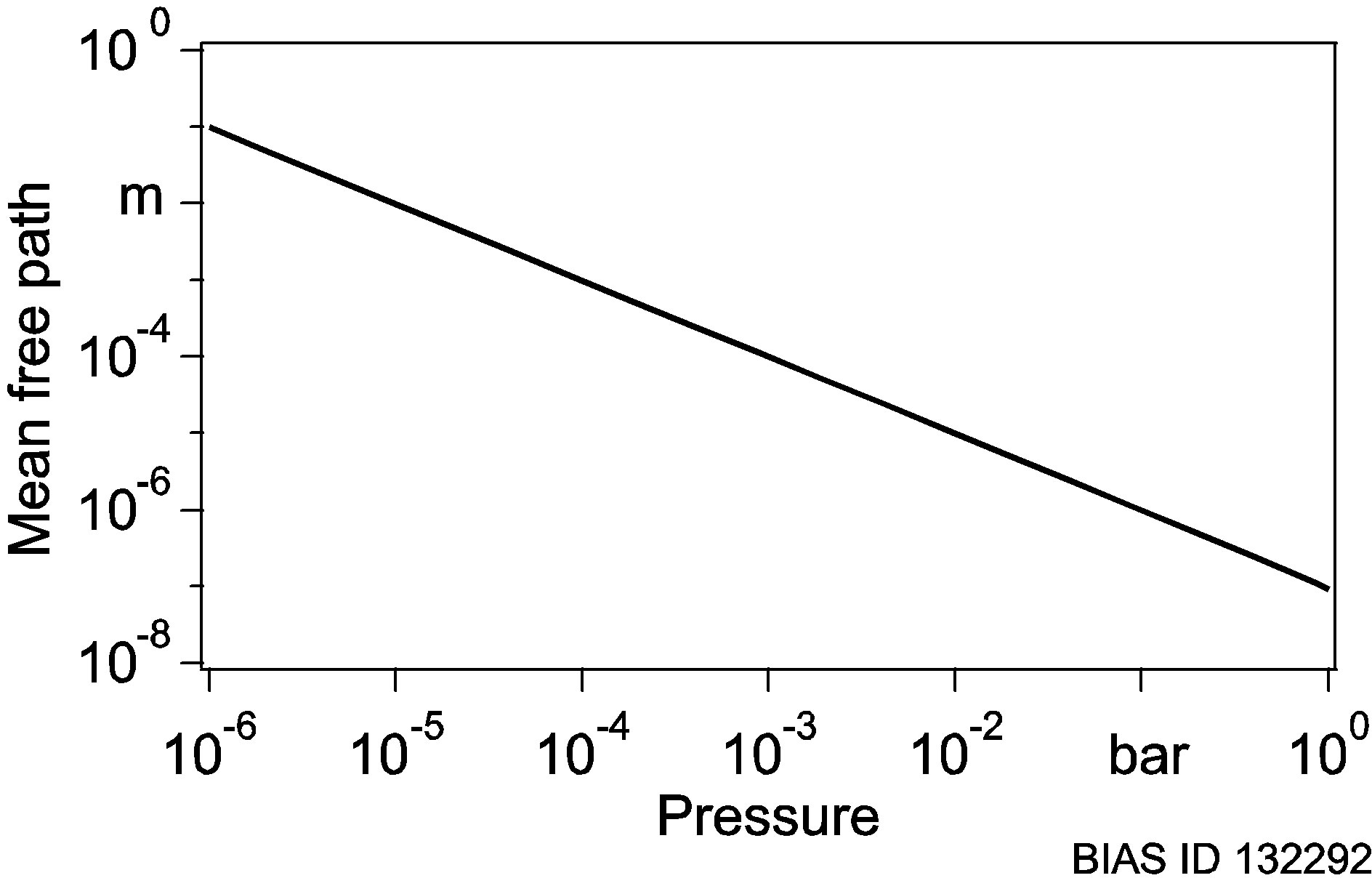
Figure 3. Mean free path in dependence of the pressure.
will be, thus allowing smaller locally halogenated structures. In order to generate halogenated structures with feature sizes in the range of a few microns, a precursor pressure in the range of 0.1 bar 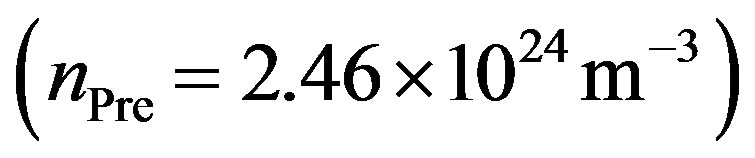 has to be adjusted.
has to be adjusted.
5. Conclusion
It was shown theoretically, that the investigated process of UV laser based halogenation using a nonreactive precursor is capable of halogenating a polymer in a singlestep process locally. With this, a polymer with tailored characteristics over the surface can be fabricated. This opens new possibilities in the field of micro droplet handling and other application in which a locally modified wettability play an important role like polymeric liquid sensors.
Acknowledgements
The authors gratefully acknowledge the financial support for this work by the German research foundation (DFG) under the grant VO 530/50-1.
REFERENCES
- L. J. Hayes and D. D. Dixon, “Surface Tension versus Barrier Property for Fluorinated Surfaces,” Journal of Applied Polymer Science, Vol. 22, No. 4, 1978, pp. 1007‑1013. http://dx.doi.org/10.1002/app.1978.070220411
- E. Liston, L. Martinu and M. Wertheimer, “Plasma Surface Modification of Polymers for Improved Adhesion: A Critical Review,” Journal of Adhesion Science and Technology, Vol. 7, No. 10, 1993, pp. 1091‑1127. http://dx.doi.org/10.1163/156856193X00600
- R. Jourdain, M. Castelli, P. Shore, P. Sommer and D. Proscia, “Reactive Atom Plasma (RAP) Figuring Machine for Meter Class Optical Surfaces,” Production Engineering, Vol. 7, No. 6, 2013, pp. 665-673. http://dx.doi.org/10.1007/s11740-013-0467-1
- T. Ikegame and M. Murahara, “ArF Excimer Laser and Xe2* Excimer Lamp Induced Photochemical Fluorination of Polyimide Film,” MRS Proceedings, Vol. 544, No. 1, 1998, pp. 227‑232. http://dx.doi.org/10.1557/PROC-544-227
- K. Tanizawa and M. Murahara, “Laser-Induced Photochemical Surface Modification of Intraocular Lens for Blocking After-Cataract,” MRS Proceedings, Vol. 735, No. 1, 2002, pp. 117‑122.
- C. Wochnowski, M. D. Ferdinando, C. Giolli, F. Vollertsen and U. Bardi, “UV-Laser-Assisted Liquid Phase Fluorination of PMMA,” Applied Surface Science, Vol. 253, No. 24, 2007, pp. 9435‑9442. http://dx.doi.org/10.1016/j.apsusc.2007.06.017
- J. Ackerhalt and J. Eberly, “Coherence versus Incoherence in Stepwise Laser Excitation of Atoms and Molecules,” Physical Review A, Vol. 14, No. 5, 1976, pp. 1705‑1710. http://dx.doi.org/10.1103/PhysRevA.14.1705
- W. K. Bischel, L. J. Jusinski, M. N. Spencer and D. J. Eckstrom, “Absolute Two-Photon Ionization Yields for Selected Organic Molecules at 248 nm,” Journal of the Optical Society of America B, Vol. 2, No. 6, 1985, pp. 877‑885. http://dx.doi.org/10.1364/JOSAB.2.000877
- J. P. Reilly and K. L. Kompa, “Laser Induced Multiphoton Ionization Mass Spectrum of Benzene,” The Journal of Chemical Physics, Vol. 73, No. 11, 1980, pp. 5468‑5476. http://dx.doi.org/10.1063/1.440092
- M. Rossi and D. J. Eckstrom, “Quantitative Aspects of Benzene Photoionization at 248 nm,” Chemical Physics Letters, Vol. 120, No. 2, 1985, pp. 118‑123. http://dx.doi.org/10.1016/0009-2614(85)87025-1
- D. S. Zakheim and P. M. Johnson, “Rate Equation Modelling of Molecular Multiphoton Ionization Dynamics,” Chemical Physics, Vol. 46, No. 3, 1980, pp. 263‑272. http://dx.doi.org/10.1016/0301-0104(80)85202-5

