Modeling and Numerical Simulation of Material Science
Vol. 3 No. 3 (2013) , Article ID: 33829 , 6 pages DOI:10.4236/mnsms.2013.33011
Ballistic Behavior of Heracron®-Based Composites: Effect of the Number Multifilaments on High-Speed Projectiles
Samsung Electronics, Suwon, South Korea
Email: staach@dreamwiz.com
Copyright © 2013 Jung Seop Lim. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 1, 2013; revised June 2, 2013; accepted June 10, 2013
Keywords: Aramid Fiber; Ballistic Behavior; Heracron; Soft Armor
ABSTRACT
In this study, two Heracron® woven fabrics, HT840-1 and HT840-2, were fabricated with different multifilament fibers, and their resistance to ballistic impact was investigated. For the same weight and number of plies, the HT840-2 fabric showed improved ballistic properties, compared with HT840-1; this result is contrary to the fiber and fabric properties. With the exception of the yarn’s physical properties, this behavior can be explained in terms of the number of multifilaments, which strongly influenced the ballistic mechanism, i.e., a greater number of multifilament fibers facilitates energy dissipation from a high-speed ballistic projectile. In summary, establishing this optimal number of multifilaments is the key to optimizing the ballistic properties of any given fabric.
1. Introduction
Aramid poly (p-phenylene terephthalamide) or PPTA consists of relatively rigid polymer chains with linked benzene rings and amide bonds. This structure affords aramid fibers high tenacity, high modulus, and toughness [1-3]. Based on these merits, aramid fibers are used in ballistic armor materials. Figure 1 shows the chemical structure of aramid fibers.
Generally, ballistic materials can be divided into hard and soft armors [4-6]. Unlike traditional structural composites, hard armors, also known as armor-grade composites, contain only 20% by weight matrix, and are made to readily delaminate. Conversely, soft armors consist of multilayered, woven textiles, and are used to protect against various types of bullets.
The ability of a woven fabric to protect against bullets depends primarily on the mechanical properties of the yarn, such as the tenacity, tensile modulus, and toughness. However, Laible [7] demonstrated that “the relationship between the mechanical properties of a yarn and the ballistic resistance of a plied fabric from such yarn has never been established”; i.e., other factors may exist that influence ballistic performance. Generally, the energy absorption mechanism of soft armor depends on several additional factors, such as the weave pattern, the number of fabric plies, and the weave density. Weave patterns used in ballistic applications are usually plain and basket weaves. Fabrics with unbalanced weaves typically yield inferior ballistic performance [8]. Lim et al. [9] investigated ballistic impacts on multiple systems to characterize the reinforcement effect of multiple layers. They concluded that the inter-ply friction inhibited the sideways motion of the yarns, resulting in an increased resistance to ballistic penetration. Weave density, which refers to the number of yarns per unit dimension along the principal yarn directions, affects the areal density of the fabric and the crimp. Shockey et al. [10] concluded that the energy absorbed by a fabric was proportional to the fabric’s areal density.
Our research group previously compared the effect of the weaving density of aramid fabrics on their resistance to ballistic impacts. It was demonstrated that the existence of an optimal weave minimizes damage to both the yarn and fabric. Establishing these optimal conditions can be crucial in implementing better ballistic properties into fabrics [11]. Yarn crimp refers to the degree of yarn undulation, and is a property of the weave. Tan et al. [12] compared two methods of modeling crimp using empirical results. They concluded that accounting for crimp by modeling the linear elements in a zigzag manner yielded more accurate results than trying to account for crimp as a constitutive property.
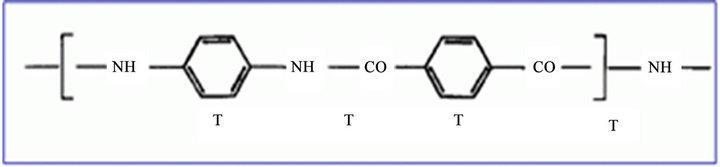
Figure 1. Chemical structure of aramid.
However, little has been reported regarding correlations between ballistic properties and multifilament aramid woven fabrics. Furthermore, a comparative study of ballistic performance has not been carried out that accounts for both fabric properties and individual yarn properties. In the current study, two types of aramid woven fabrics, each with a different number of multifilaments, were prepared, and the influences of the number of multifilaments on the fabric properties and ballistic behavior were ascertained. This study provides fundamental information on how the number of multifilaments regulates fabric properties and the ballistic behavior of aramid woven fabrics.
2. Experimental Section
2.1. Materials
Aramid fibers (trademark Heracron®) were produced by Kolon Inc. (Kwach’on, Korea) with a fiber fineness of 840 denier. Table 1 shows some of the basic properties of two Heracron® filament fibers, each composed of 666 and 1000 monofilament fibers, respectively. As shown in Figure 1, the two Heracron® yarns had comparable tenacity, elongation, and Young’s modulus. Two types of fabrics, HT840-1 and HT840-2, were woven from the fibers for ballistic tests. The two fabrics had the same weave structure, fiber fineness, and weaving density. The detailed fabric properties are described below. To eliminate finishing oil and surface contamination, the fabrics were washed using an industrial scouring process.
2.2. Analysis
Filament fiber tests were performed in accordance with ASTM Standard D2256-97 (ASTM 2000). Each fiber specimen had an initial length of 50 cm. At the start of the test, the middle 25 cm of the fiber spanned between the instrument grips. The crosshead separation rate was maintained at 2 mm∙s−1, and the specimen was elongated until rupture. All of the specimens were twisted at a rate of 1.2 turns cm−1. The data from 20 independent measurements were expressed as an average with a single standard deviation. Fabric tests were performed in accordance with ISO 13934-1. All sample fabrics were created from the HT840 fabrics using the ravel strip method. Each sample had an initial length of 1.2 m and a width of 50 cm. A 50-mm length at each end of each sample was clamped into place with a fabric grip. The
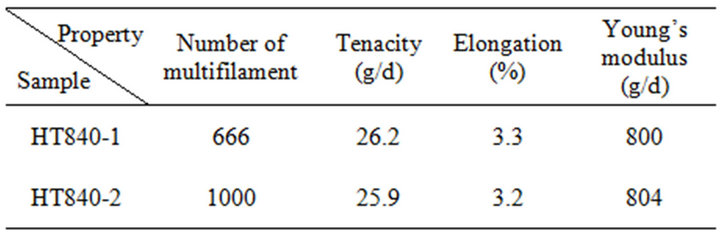
Table 1. Basic properties of two Heracron® yarns.
sample was then wrapped twice around each grip. During each test, the load frame crosshead moved at constant rate of 2 mm∙s−1. Samples were pulled until rupture. Twelve samples in total were tested. Six were elongated along the warp, with the weft running along the width. The other six were elongated along the weft, with the warp running along the fabric width. Ballistic shooting tests were performed on 32-ply samples of each of the two fabrics (HT840-1 and HT840-2) in accordance with NIJ Standard-0101.06, “Ballistic Resistance of Body Armor, Level 3A Methods”. Tests were performed with 44-Magnum semi-jacketed hollow-point (SJHP) bullets, with a mass of 15.6 g (240 g) impacting the fabrics at a velocity of 436 ± 9 m∙s−1 (1430 ± 30 ft∙s−1). Six bullets were shot into each sample. After shooting, the depth of the puncture and the back deformation signature (BFS) formed on the backing material were measured. All tests were conducted at the H.P. White Laboratory, Inc. (Street, MD, USA).
3. Results and Discussion
3.1. Fiber and Fabric Properties
Aramid fibers consist of highly oriented and ordered crystalline polymer chains, resulting in a rigid structure that does not endure bending. Therefore, aramid yarn is usually composed of one multifilament fiber, in conjunction with a large number of monofilament fibers. Generally, an aramid monofiber may be divided by its skin— core fibril structure. It is known that the skin, in which the fibrils are uniformly axially oriented to the fiber axis, strongly affects the fiber’s physical properties [1]. In contrast, fibril in the fiber core are imperfectly packed and ordered. Both the skin and core properties contribute to the strength and resilience of the fiber. Therefore, it is important to comprehend the various properties of monofilament fibers, as well as multifilament yarns. Table 2 lists the properties of Heracron® monofilament fibers. HT840-1, with a thicker monofilament fiber density, displays superior physical properties, compared with HT840-2. This suggests that the HT840-1 fiber is better suited for skin structure fabrication than that of HT840-2 during the dry-wet jet spinning process. Well oriented skin fibril may prohibit the fiber rupture and improve its physical property.
Table 3 lists the physical properties of the extracted

Table 2. Physical properties of Heracron® monofilament fiber.
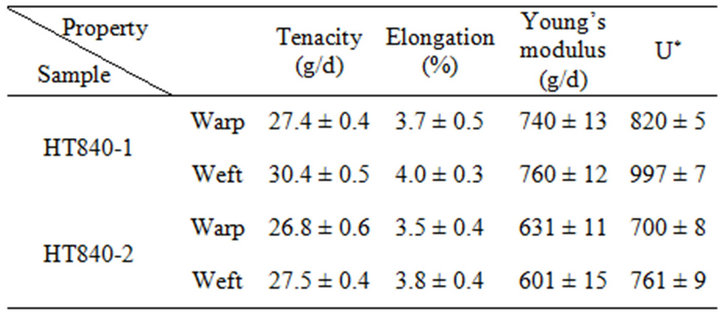
Table 3. Physical properties of extracted warp and weft yarns from Heracron® fabrics.
warp and weft from the Heracron® fabrics. All of the specimens were created by the ravel strip method and were pulled until rupture; 20 specimens were tested. Irrespective of warp and weft, HT840-1 had higher tenacity, elongation, and Young’s modulus, compared with HT840-2. This result supports the notion that the properties of the monofilament fiber are reflected in the properties of the multifilament yarn. The above data were used to calculate the dimensionless fiber property, U*, defined as the product of the specific fiber toughness and the strain-wave velocity, according to the follow equation:
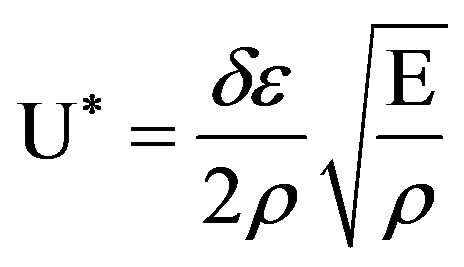
where δ is the fiber ultimate tensile strength, ε is the fiber ultimate tensile strain, E is Young’s modulus, and ρ is the fiber density. U* can generally be used to qualitatively assess the physical performance of fibers. Note that the U* value of HT840-2 was lower than that of HT840-1. Cunnif [11,13] demonstrated that U* may be a major factor that relates ballistic impact performance to fiber mechanical properties, independent of other parameters, such as impacting projectile mass, presented area, or areal density. Although the exact relationship between the mechanical properties of a yarn and the ballistic resistance of a plied fabric from such yarn has never been established, the conclusion that the mechanical properties of the yarn would affect a fabric’s ballistic characteristics seems obvious.
Table 4 summarizes the physical properties of the HT840-1 and HT840-2 fabrics. The thicknesses and areal densities of the two fabrics were the same, but the fabric tensile strength, generally considered the most important fabric property, differed; HT840-1 was stronger than HT840-2 along both the warp and weft directions. This suggests that the fabric tensile strength may be strongly influenced by the individual yarn’s physical properties. Hence, we anticipated that HT840-1 would efficiently dissipate the energy from a high-speed ballistic projectile, resulting in better ballistic behavior compared with HT840-2.
3.2. Ballistic Properties
A comparison of ballistic properties can usually be made by analyzing crushed bullets retrieved from the tested fabrics. An increase in the bullet crush may be due to a better degree of energy propagation and dissipation by the fabric, which would indicate superior ballistic performance. Figure 2 shows a bottom view of crushed bullets retrieved from the seventh ply of the HT840 fabrics. The bullet retrieved from HT840-2 was crushed to a greater degree than the bullet retrieved from HT840-1, demonstrating that HT840-2 had better energy absorption capability. Note that this result is contrary to the fiber and fabric mechanical results.
We compared the ballistic properties of the two HT840 fabrics by examining them directly. Figure 3 shows perforated regions in the HT840 fabrics (4-ply) impacted by the projectile. More yarn was broken and fibrilized in the HT840-1 fabric, compared with HT840-2. Moreover, the cross shape, without perforation, was still intact at the surface of the HT840-2 fabric. This demon
 (a) (b)
(a) (b)
Figure 2. A bottom view of the crushed bullets retrieved from HT840 fabrics. (a) HT840-1; (b) HT840-2.
 (a) (b)
(a) (b)
Figure 3. Perforated regions of two HT-840 fabrics impacted by the projectile (4-ply). (a) HT840-1 (4-ply); (b) HT840- 2 (4-ply).
strates that the HT840-1 fabric experienced more damage from the high-speed projectile. Similar results are shown in Figure 4, which displays the perforated regions in the HT840 fabrics (9-ply) impacted by the projectile. Very little damage (e.g., breakage and fibril) occurred in the HT840-2 fabric, compared with HT840-1.
Upon impaction by a projectile, fabrics generally fail through perforation mechanisms, which reflect both the energy absorption capability and ballistic performance of the fabric. An increase in the number of broken yarns and an appearance of perforated regions may indicate that the kinetic energy of the bullet could not be absorbed by the fabric efficiently. The results reported herein show that the kinetic energy of a bullet is more efficiently dissipated in the HT840-2 fabric, resulting in ballistic properties superior to those of HT840-1.
Figure 5 shows a photograph of the ninth ply removed from each of the HT840 fabrics; the arrow indicates yarns that were pulled from the fabric. When a woven fabric is subjected to a ballistic impact, it becomes deformed both vertically and horizontally by the kinetic energy of the bullet. The initial deformation at the site of impact spreads outward as long as the bullet’s speed is not sufficient to allow penetration of the fabric. Under these circumstances, the kinetic energy of the bullet will be completely absorbed by the fabric. However, at a suf-
 (a) (b)
(a) (b)
Figure 4. Perforated regions of two HT-840 fabrics impacted by the projectile (9-ply). (a) HT840-1 (9-ply); (b) HT840-2 (9-ply).
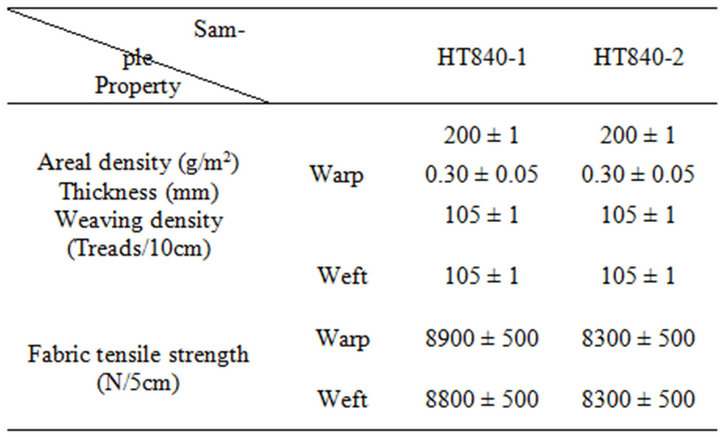
Table 4. Physical properties of Heracron® woven fabrics.
ficiently high velocity, the bullet will pass through the fabric. Relative to HT840-2, the pull-out zone of HT840- 1 was clearly apparent. Additionally, a greater number of pulled-out yarns were observed along the bottom edge. The impact energy dissipates through yarn pullout, a consequence of yarn stretching. The pull-out zone is cross-shaped, the center being the impact point [14]. The high bullet resistance of a fabric is determined by the pulling-out of yarns impacted by the bullet. In these zones, the bullet energy is transferred to the fibers. The amount of energy transferred to the fabric layer increases with the length and width of the pull-out zone as the bullet decelerates. Based on this finding, we can demonstrate that HT840-2 possesses a higher capacity for impact energy than HT840-1.
Table 5 summarizes the ballistic properties of the two Heracron® woven fabrics. Generally, the deformation of ballistic armor during impact can be assessed by measuring the back deformation signature (BFS) [15]. The BFS of HT840-1 was deeper than that of HT840-2, indicating that the kinetic energy of the bullet was not efficiently dispersed over a large area of the fabric. The energy absorption characteristics of a fabric system under ballistic impact depends on many factors, including the material properties of the constituent fibers, the woven
 (a) (b)
(a) (b)
Figure 5. Photograph of the ninth layer taken out of the two HT840 fabrics. (a) HT840-1 (9-ply); (b) HT840-2 (9-ply).
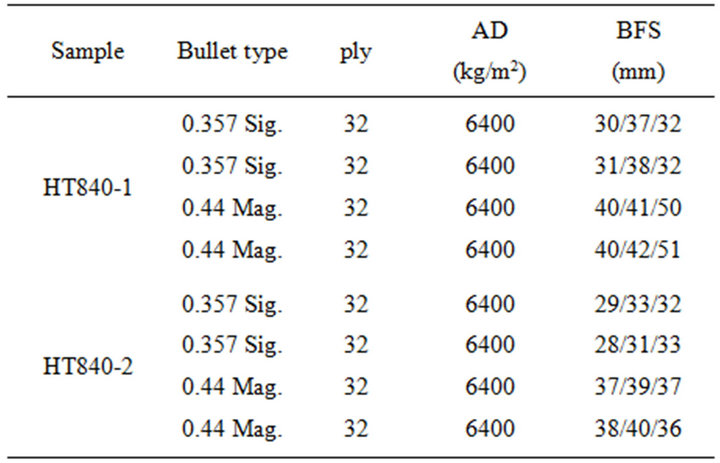
Table 5. Ballistic property of Heracron® woven fabrics.
structure of the fabric, the projectile geometry, the impact velocity, the number of plies, and the far-field boundary conditions. In the current study, all of these parameters were held constant with the exception of both yarn’s physical properties and multifilament fiber number.
The physical properties of the HT840-1 fiber, i.e., its tenacity, elongation, and Young’s modulus, were superior to those of HT840-2. Therefore, we anticipated that the ballistic properties of HT840-1 would be superior to HT840-2; however, this was not the case. Instead, our results suggested that better performance of the HT840-2 fabric was achieved due to the multifilament fiber. Traditionally, better ballistic performance has been achieved using greater numbers of multifilament fibers, which have been found to facilitate energy dissipation from high-speed ballistic projectiles. Having a larger number of multifilament fibers appears to provide better protection from high-speed rotating projectiles. The results given herein suggest that the lower ballistic resistance of HT840-1 may be explained by an insufficient number of multifilament fibers. Figure 6 shows the mimetic diagrams of kinetic energy absorption and dispersion by the fabrics.
Of course, ballistic performance improvements have also been achieved through the use of high-performance yarns that have been specifically engineered to have higher tensile strengths and/or increased elongations before breakage. However, the combination of the yarn’s physical properties and other parameters must be carefully investigated. In summary, establishing the optimal number of multifilaments for a given fabric is one of the main factors influencing the ballistic resistance properties of the fabric.
4. Conclusions
Two Heracron® woven fabrics with different numbers of multifilament fibers were assessed for their resistance to ballistic impact. The results may be summarized as follows:
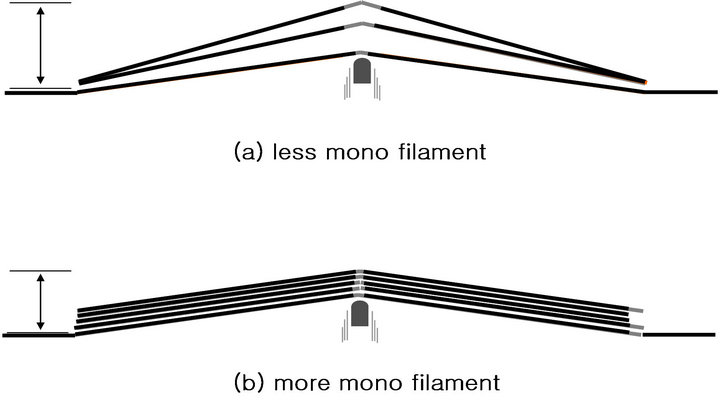
Figure 6. Mimetic diagrams of kinetic energy absorption and dispersion by a fabric.
1) The HT840-1 fiber and its fabric demonstrated higher values of tenacity, elongation, and Young’s modulus. However, the kinetic energy of a bullet was more efficiently dissipated in the HT840-2 fabric, resulting in improved ballistic resistance properties, compared with those of HT840-1.
2) The results given herein suggest that the lower ballistic resistance of HT840-1 may be explained by an insufficient number of multifilament fibers for accomplishing the desired ballistic resistance.
3) Establishing this optimal number of multifilaments is key to optimizing the ballistic properties of any given fabric.
REFERENCES
- H. H. Yang and K. A. Fiber, “Aramid Fiber,” John Wiley & Sons Ltd., Chichester, 1993.
- P. J. de Lang, P. G. Akker, E. Mäder, S. L. Gao, W. Prasithphol and R. J. Young, “Controlled Interfacial Adhesion of Twaron® Aramid Fibers in Composites by the Finish Formulation,” Composites Science and Technology, Vol. 67, 2007, pp. 2027-2035. doi:10.1016/j.compscitech.2006.11.018
- Y. Rao, A. J. Waddon and R. J. Farris, “The Evaluation of Structure and Properties in Poly(p-phenylene terephthalamide) Fibers,” Polymer, Vol. 42, 2001, pp. 5925- 5935.
- C. Y. Yue and K. Padmanabhan, “Interfacial Studies on Surface Modified Kevlar Fibre/Epoxy Matrix Composites,” Composite Part B, Vol. 30, No. 2, 1999, pp. 205- 217. doi:10.1016/S1359-8368(98)00053-5
- T. K. Lin, S. J. Wu, J. S. Lai and S. S. Shyu, “The Effect of Chemical Treatment on Reinforcement/Matrix Interaction in Kevlar-Fiber/Bismaleide Composites,” Composites Science and Technology, Vol. 60, No. 9, 2000, pp. 1873-1878. doi:10.1016/S0266-3538(00)00074-9
- R. Park and J. S. Jang, “Impact Behavior of Aramid Fiber/Glass Fiber Hybrid Composites: The Effect of Staking Sequence,” Colloid & Polymer, Vol. 22, No. 1, 2001, pp. 80-89.
- R. C. Laible, “Fibrous Armor,” In: R. C. Laible, Ed., Ballistic Materials and Penetration Mechanics, Elsevier Scientific Publishing Co., New York, 1980, pp. 73-115. doi:10.1016/B978-0-444-41928-6.50009-0
- P. M. Cunniff, “An Analysis of the System Effects in Woven Fabrics under Ballistic Impact,” Textile Research Journal, Vol. 62, No. 9, 1992, pp. 495-509.
- C. T. Lim, V. B. C. Tan and C. H. Cheong, “Perforation of High-Strength Double-Ply Fabric System by Varying Shaped Projectiles,” International Journal of Impact Engineering, Vol. 27, No. 6, 2002, pp. 577-591. doi:10.1016/S0734-743X(02)00004-0
- D. A. Shockey, D. C. Erlich and J. W. Simons, “Improved Barriers to Turbine Engine Fragments: Interim Report III,” Report No. DOT/FAA/AR-99/8, 2004.
- J. S. Lim, B. H. Lee, C. B. Lee and I. S. Han, “Effect of the Weaving Density of Aramid Fabrics on Their Resistance to Ballistic Impacts,” Engineering, Vol. 4, 2012, pp. 944-949. doi:10.4236/eng.2012.412A119
- V. C. Tan, V. P. W. Shim and X. Zeng, “Modeling Crimp in Woven Fabrics Subjected to Ballistic Impact,” International Journal of Impact Engineering, Vol. 32, No. 1-4, 2005, pp. 561-574. doi:10.1016/j.ijimpeng.2005.06.008
- P. M. Cunniff, “Dimensionless Parameters for Optimization of Textile-Based Body Armor Systems,” Proceedings of the 18th International Symposium on Ballistics, San Antonio, 1999, pp. 1303-1310.
- S. Bazhennov, “Dissipation of Energy by Bullet Proof Aramid Fabric,” Journal of Materials Science, Vol. 32, No. 15, 1997, pp. 4167-4173. doi:10.1023/A:1018674528993
- H. L. Gower, D. S. Cronin and A. Plumtree, “Ballistic Impact Response of Laminated Composite Panels,” International Journal of Impact Engineering, Vol. 35, No. 9, 2008, pp. 1000-1008. doi:10.1016/j.ijimpeng.2007.07.007

