Modeling and Numerical Simulation of Material Science
Vol. 2 No. 3 (2012) , Article ID: 21382 , 7 pages DOI:10.4236/mnsms.2012.23007
Theoretical Study on the Origins of the Gap Bowing in MgxZn1–xO Alloys
Laboratoire de Microscopie, Microanalyse et Spectroscopie Moleculaire
Faculté des Sciences, Département de Physique, Sidi-bel-abbes Algeria
Djilali-Liabes University of Sidi-Bel-Abbes, Algeria
Email: benkabouz@yahoo.com
Received April 9, 2012; revised May 12, 2012; accepted May 23, 2012
Keywords: FP-LMTO Method; Structural and Electronic Properties; MgxZn1-xO Alloy; Bowing
ABSTRACT
The full potential linear muffin-tin orbital (FP-LMTO) method was applied to study the structural and electronic properties of the compounds MgO, ZnO and their alloy MgxZn1–xO in the zincblende and NaCl structures. Results are obtained using the local density approximation (LDA), the ground-state properties like lattice constant and bulk modulus obtained agree very well with experimental and other theoretical calculations. The effect of composition on lattice constant from Vegard’s law and the bulk modulus was investigated. The microscopic origins of the gap bowing were explained by using the approach of Zunger and co-workers. It is concluded that the energy band gap bowing is primarily due to chemical charge-transfer effect. Contribution of volume deformation and structural relaxation to the gap bowing parameter is found to be very small.
1. Introduction
II-VI semiconductors have been of growing interest because of their wide band gap character and the potential applications for optoelectronic devices.
Currently, devices composed from the binary oxides of Mg, Zn, Cd and related alloys are generating considerable interest as they can provide, in principle, an accessible direct band-gap range from around 2.3 eV to 7.7 eV [1].
This makes them promising candidates even for deep ultrat violet (UV) lighting applications [2,3].
The B1 phase is found to be stable over all (Mg,Zn)O compositions [4], as expected from the preferences of the binary oxides. However, there exists the serious problem of phase separation due to the large dissimilarity of stable cristal structure, thay is, wurtzite for ZnO and rocksalt for MgO.
Many ab initio calculations of the parent compounds, i.e., MgO and ZnO can be found in the literature [4,5]. To the best of our knowledge, there is no theoretical work on the structural and electronic properties of MgxZn1-xO alloy using FP-LMTO method.
Very recently, Fritsh et al. [6] have calculated the electronic properties of the rocksalt MgxZn1–xO alloy using empirical pseudopotential method, and Amrani et al. [7] using FP-LAPW method.
Many calculations using (FP-LMTO) have been done to characterize the structural, electronic and optical properties in four phases of compouds: RuC [8], and CuCl, CuBr, CuI [9] and of the cubic BexZn1–xSe alloy in zincblende structure [10].
Conserning, this method FP-LMTO, “all electron” it is meant that all electrons in the solid are considered in the calculation of electron density and total energy (as opposed, for instance, to a pseudo-potential method, where only the valence electrons are considered), and the term “full potential” implies that no approximation is made to the shape of the electron density or the electronic potential.
The present study focus mainly on the compositions dependence on the structural and electronic properties of MgxZn1–xO ternary alloy in the NaCl structure, using the full-potential linear muffin-tin orbital (FP-LMTO) method, within the local-density approximation (LDA) scheme, to determine a set of physical parameters of MgO, ZnO and their ternary alloy, namely the optimized lattice constant, bulk modulus, energy band gap and gap bowing.
A brief description of the computational details and methodology are given in Section 2. The most relevant results obtained for the structural and electronic properties for MgxZn1–xO in rocksalt phase are presented and discussed in Section 3. The conclusion is given in Section 4.
2. Method of Calculations
The calculations reported here were carried out using the ab initio full-potential linear muffin-tin orbital (FP-LMTO) method [11] as implemented in the Lmtart code [12].
The exchange-correlation potential was treated by the local density approximation (LDA) developed by Perdew and wang [13]. This is an improved method compared to previous (LMTO) methods.
The FP-LMTO method treats muffin-tin spheres and interstitial regions on the same footing, leading to improvements in the precision of the eingen-values. At the same time, the FP-LMTO method, in which the space is divided into an interstitial regions (IR) and non overlapping muffin-tin spheres (MTS) surrounding the atomic sites, uses a more complete basis than its predecessors. In the IR regions, the basis functions are represented by Fourier series. Inside the MTS spheres, the basis functions are represented in terms of numerical solutions of the radial Schrödinger equation for the spherical part of the potential multiplied by spherical harmonics.
The charge density and the potential are represented inside the MTS by spherical harmonics up to lmax = 6. The integrals over the Brillouin zone are performed up to 35 special k-points for binary compounds and 27 special k-points for the alloys in irreducible Brillouin zone (IBZ), using the Blöchl’s modified tetrahedron method [14]. The self-consistent calculations are consisidered to be converged when the total energy of the system is stable within 10 - 5 Ry. In order to avoid the overlap of atomic spheres the MTS radius for each atomic position is taken to be different for each case.
Both the plane waves cut-off are varied to ensure the total energy convergence. The values of the sphere radii (MTS), number of plane waves (NPLW), used in our calculation are summarized in Table 1.
3. Results and Discussions
3.1. Structural Properties
We first calculated structural properties of the binary compounds ZnO and MgO in the rocksalt (B1) phases.
Then, the alloy was simulated for the compositions x = 0.25, 0.50 and 0.75 by applying special Quasi-random Sheme proposed by Zunger et al. [15]. This scheme has been applied to many semiconductors alloys [16-22] successfully. We calculated the equilibrium structural parameters (lattice constant and bulk modulus) for the parent binary compounds MgO, ZnO and their ternary alloy.
As for the semiconductor ternary alloy in the type BxA1-xC we have started our FP-LMTO calculations of the structural properties with B1 structure. We have chosen the basic cubic cell as the unit cell.
In the unit cell there are four C anions and three A and one B, two A and two B, and one A and three B cations respectively, for x = 0.25, 0.50 and 0.75. And the atomic positions for MgxZn1–xO are given in Table 2.
We have assumed that the atoms are located at the ideal lattice sites in ordered positions.
The calculated lattice constant, bulk modulus and first-order pressure derivatives of bulk modulus (B’), for the ZnO, MgO and MgxZn1–xO alloy are summarized in Table 3. For the considered structures, we perform the structural optimization by minimizing the total energy with respect to unit cell parameters.
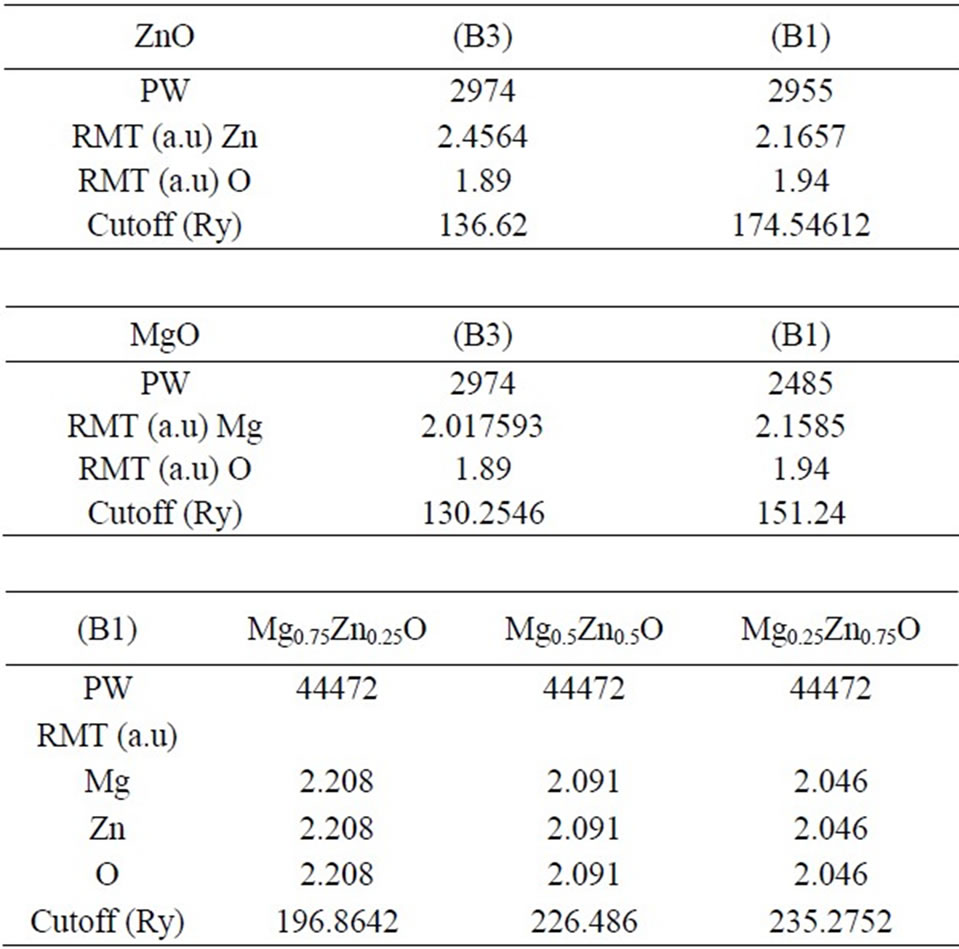
Table 1. The plane wave number PW, energy cuttof (in Ry) and the muffin-tin radius (RMT) (in a.u) used in calculations for binary MgO, ZnO and their alloy in zincblende (B3) and rocksalt (B1) structures.
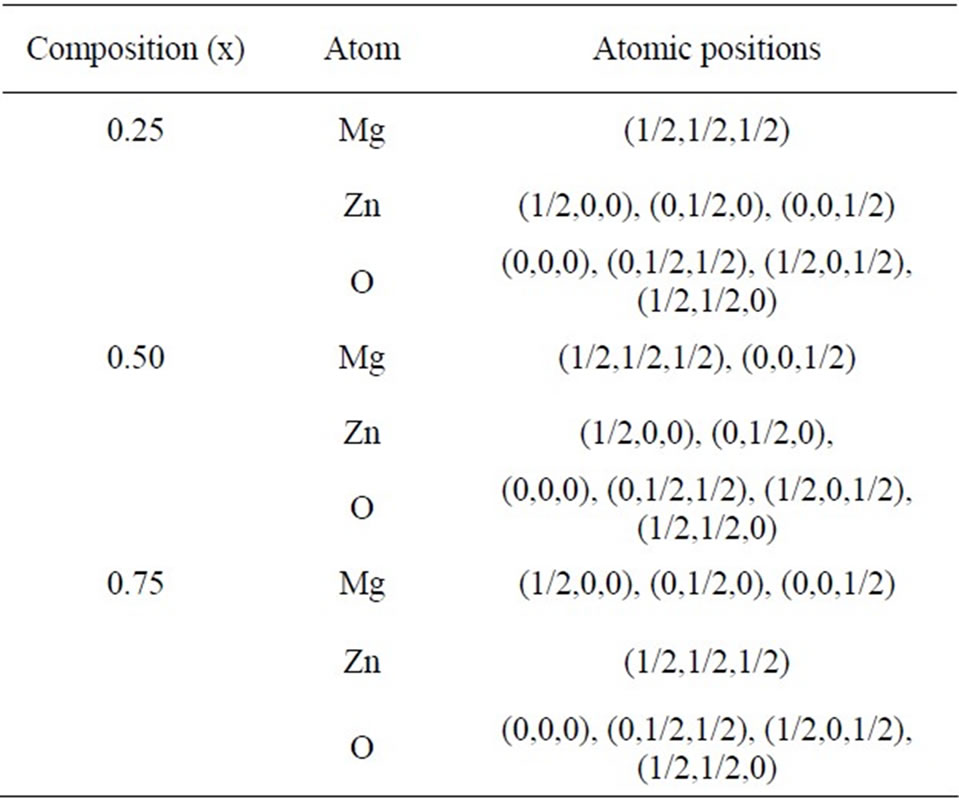
Table 2. Atomic positions in the MgxZn1-xO alloy.

Table 3. Calculated lattice parameter aeq (Å), bulk modulus B (GPa) and first-order pressure derivatives of bulk modulus (B’) for the ZnO, MgO and MgXZn1-x O alloy. aRef [26], bRef [27], cRef [28], dRef [29], eRef[30], fRef [31], gRef [32], hRef [33], iRef [7].
The calculated lattice constant, bulk modulus and its pressure derivative for each x of the MgxZn1–xO with respect to the cell parameters and also the atomic positions.
The total energies were calculated as a function of volume and were fitted to the universal Murnaghan’s equation of state [23]. The predicted lattice parameters for the binary compounds are in reasonable agreement with those measured experimentally as well as with those calculated from theoretical methods.
However, we have a small underestimation of the lattice parameters, when we compare our results to the experimental data, this is due essentially to the use of the LDA. The calculated values of the bulk modulus decrease from ZnO to MgO, i.e. from the higher to the lower atomic number. This suggests that ZnO is more rigid than MgO.
Usually, in the treatment of alloy problems, it is assumed that the atoms are located at ideal lattice sites and the lattice constants of alloys should vary linearly with compositions x according to the so-called Vegard’s law [24] :
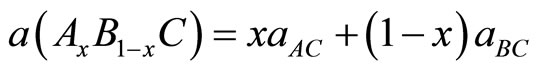
where 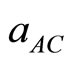 and
and  are the equilibrium lattice constants of the binary compounds AC and BC respectively, and a(AxB1-xC) is the alloy lattice constant.
are the equilibrium lattice constants of the binary compounds AC and BC respectively, and a(AxB1-xC) is the alloy lattice constant.
The calculated lattice constants at different compositions, as shown in Figure 1, where well fitted with the following relation:
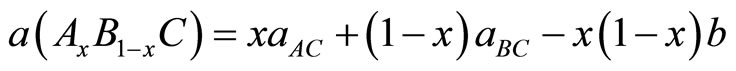
the quadratic term b represents the disorder parameter (bowing), the obtained bowing parameter b is 0.00114.
The linear dependence in x is therefore in accordance with Vegard’s Law with negligible bowing. Figure 2, show the variation of the bulk modulus versus concentration x for MgxZn1–x alloy.
The overall behaviors of the variation of the bulk modulus as a function of the composition for the MgxZn1–xO is presented in Figure 2 is compared to the results predicted by linear concentration dependence (LCD). A
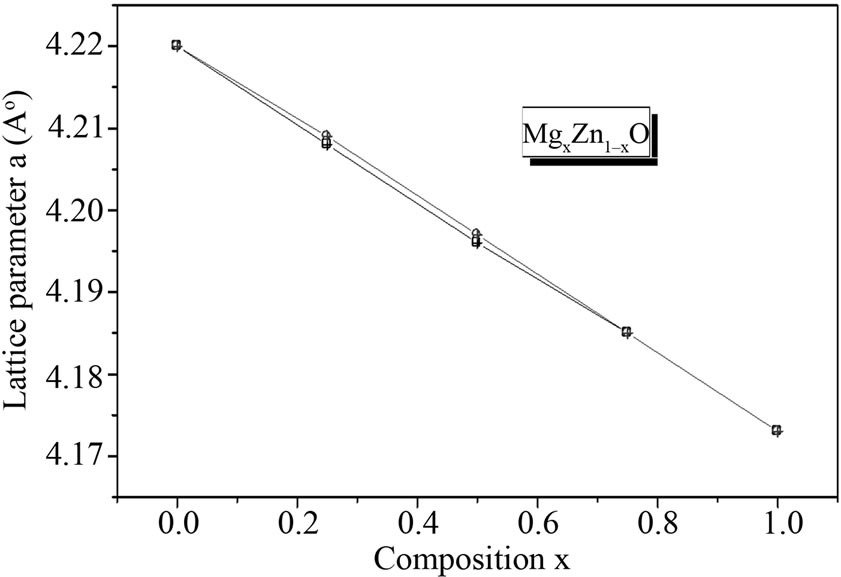
Figure 1. Composition dependence lattice constant of Mgx- Zn1-xO alloy (black line) and with VCA (red line).

Figure 2. Composition dependence of the calculated bulk modulus (solid squares) of MgxZn1-xO alloy compared with the linear composition dependence prediction (red line).
deviation from the LCD is observed with downward bowing equal to 4.19 GPa is obtained by fitting a calculated data with a polynomial of second order. This deviation from Vegard Law [24] is due to the fact that bulk modulus of ZnO is 11.2% higher than that of MgO.
To the best of our knowledge, there are no experimental work exploring the structural properties (e.g, the bulk modulus B and it pressure derivatives B’) and the bowing parameters of the of the investigated alloys, but our results are relatively close to those of Ref. [7] obtained by using the full potential-linear augmented plane wave (FP-LAPW) method.
3.2. Electronic Properties
We have calculated the band structures for the MgxZn1–x- O alloy along the high directions in the first Brillouin zone at the calculated equilibrium lattice constants.
The band structure calculations give a direct band gap Ґ - Ґ for MgO and an indirect band gap M - Ґ for ZnO and MgxZn1–xO. The calculated band gaps for all studied compositions (x = 0, 0.25, 0.50, 0.75, 1) are given in Table 4. We calculated the gap bowing by fitting the nonlinear variation of the calculated band gap versus composition x with the quadratic semi-empirical formula:
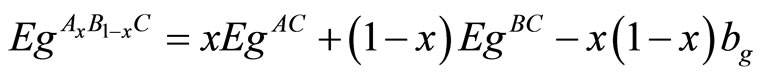 (1)
(1)
where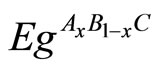 ,
,  and
and  are the energy band gaps of the ternary alloy AxB1–xC and its binary parents AC and BC, respectively. The curvature bg is commonly known as gap bowing parameter. The results shown in Figure 3. are well fitted by the expression (1), and are summarized as follows:
are the energy band gaps of the ternary alloy AxB1–xC and its binary parents AC and BC, respectively. The curvature bg is commonly known as gap bowing parameter. The results shown in Figure 3. are well fitted by the expression (1), and are summarized as follows:
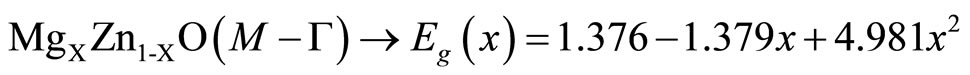 (2)
(2)
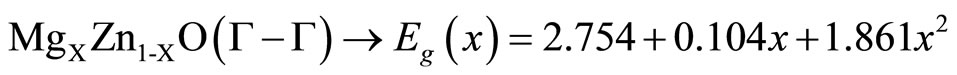 (3)
(3)
It is clear from the above equations that the direct (Ґ-Ґ) and indirect (M-Ґ) bands gaps versus concentration have a nonlinear behavior. This behavior was observed by Amrani et al. [7] by using ab initio FP-LAPW. The indirect gap has a downward bowing with a value of 4.98, and 1.86 for the direct gap.
From the Figure 3, it is clear that the crossover of indirect band gap (M - Ґ) to direct (Ґ - Ґ) is at concentration of 0.9.
In order to better understand the physical origins of the gap bowing parameter in MgxZn1–xO alloys, we follow the procedure of Bernard and Zunger [25] and decompose

Figure 3. Direct and indirect band gap energies of MgxZn1-xO alloy as a function of Mg concentration.
the total bowing parameter b into three physically distinct contributions. The overall bowing coefficient at each composition x measures the change in the band gap according to the formal reaction:
 (4)
(4)
where 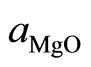 and
and ![]() are the equilibrium lattice constants of the binary compounds and
are the equilibrium lattice constants of the binary compounds and 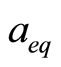 is the equilibrium lattice constant of the alloy with average composition x. Equation (4) is decomposed into three steps:
is the equilibrium lattice constant of the alloy with average composition x. Equation (4) is decomposed into three steps:
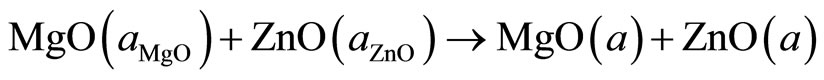 (5)
(5)
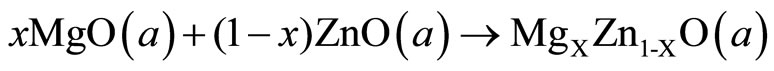 (6)
(6)
 (7)
(7)
The first step measures the volume deformation (VD) effect on the bowing. The corresponding contribution bVD to the bowing parameter represents the relative response of the band structure of the binary compounds MgO and ZnO to hydrostatic pressure, which here arises from the change of their individual equilibrium lattice constants to the alloy value a = a(x). The second contribution, the charge exchange (CE) contribution bCE, reflects the charge transfer effect which is due to the different (averaged) bonding behavior at the lattice constant a. The last contribution, the so called: structural relaxation (SR), measures changes in passing from the unrelaxed to the relaxed alloy by bSR. Consequently, the total bowing parameter is defined as:
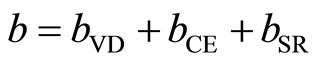 (8)
(8)
The general representation of the composition-dependent band gap of the alloy in terms of the gaps of the binary compounds EMgO(aMgO), EZnO(aZnO), and the total bowing parameter b is given by:
 (9)
(9)
This allows a splitting of the total bowing b into three contributions according to:
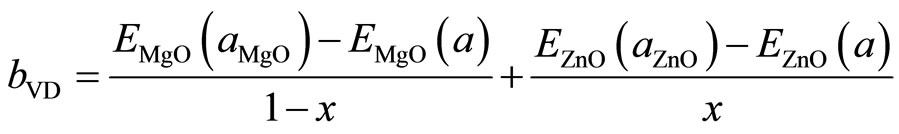 (10)
(10)
 (11)
(11)
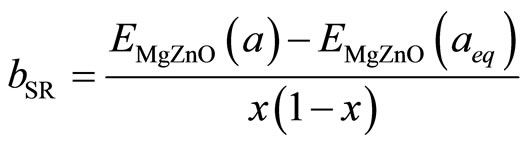 (12)
(12)
where E is the energy band gap calculated for the indicated compound with the indicated atomic positions and lattice constant aMgO, aZnO and aeq are the equilibrium lattice constants of MgO, ZnO and MgxZn1–xO alloys respectively. The lattice constant (a) is calculated by linear composition dependence rule [24] for the alloys.
Using Equations (10)-(12), the bowing coefficients b calculated at molar fractions x = 0.25, 0.50 and 0.75 for the MgxZn1–xO alloy are listed in Table 5, together with the bowing obtained using a quadratic variation of the band gap energy versus composition x. The calculated quadratic parameters of the gap bowing are in good agreement with the values found from the approach of Bernard and Zunger [25]. The charge transfer contribution bCE dominates the total gap bowing parameter in the three compositions x: (x = 0.25, 0.50 and 0.75); this is related to electronegativity mismatch between the constituting atoms: Mg (1.31), Zn (1.65) and O (3.44).The low value of bVD is related to the weak mismatch of the lattice parameters of MgO and ZnO compounds. The small contribution of the structural relaxation to the bowing parameter it due to that our calculations are for ordered structure.
4. Conclusions
In this study, we have presented a complete theoretical analysis of the structural and electronic properties of MgxZn1–xO alloys by using the FP-LMTO method within the local-density approximation (LDA). The equilibrium lattice constants, bulk modulus and first order pressure derivatives of the bulk modulus of the binary compounds and MgxZn1–xO alloy have been studied.
The energy gaps of ZnO and MgO compounds calculated with the equilibrium lattice constant, are found to be reasonable agreement with the experimental data.
We have investigated the composition dependence of the lattice constant, bulk modulus and band gap. The calculated lattice constants scale linearly with composition, showing the validity of Vegard’s linear rule in the definition of lattice constants of MgxZn1–xO alloys. A significant deviation of the bulk modulus from LCD is observed for these alloys. The gap bowing is mainly caused by the charge-transfer effect, while the volume deformation and the structural relaxation contribute at smaller magnitude.
The main advantage with a full-potential linear muffin-tin orbital (FP-LMTO) method, as described here, is that the electronic structure problem is solved with very high accuracy, so that total energies can be calculated with high precision.
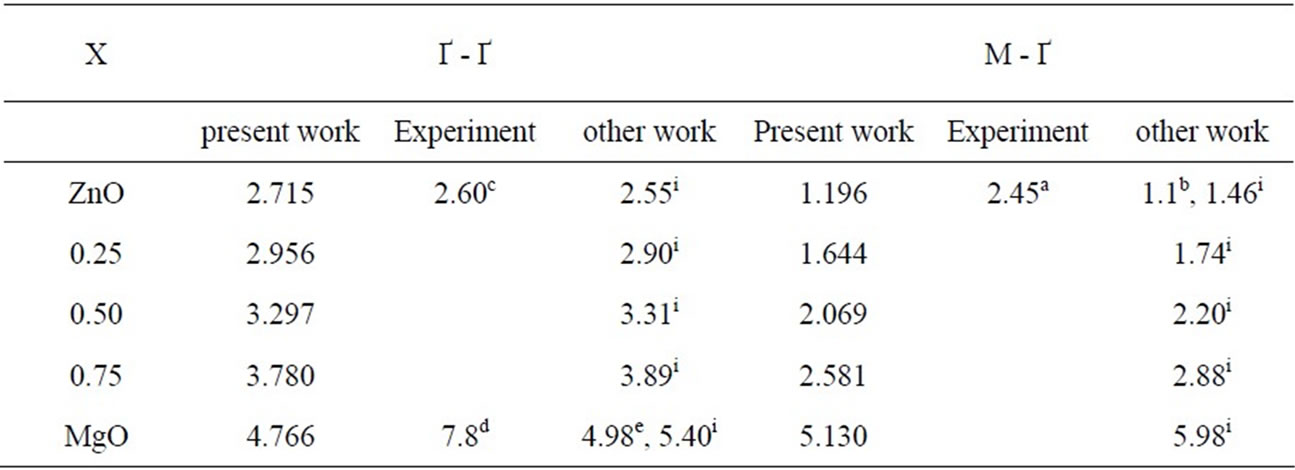
Table 4. Indirect and direct band gap energy of MgXZn1–XO alloy. aRef[34], bRef[33], cRef[ 34], dRef[35], eRef[36], iRef[7].
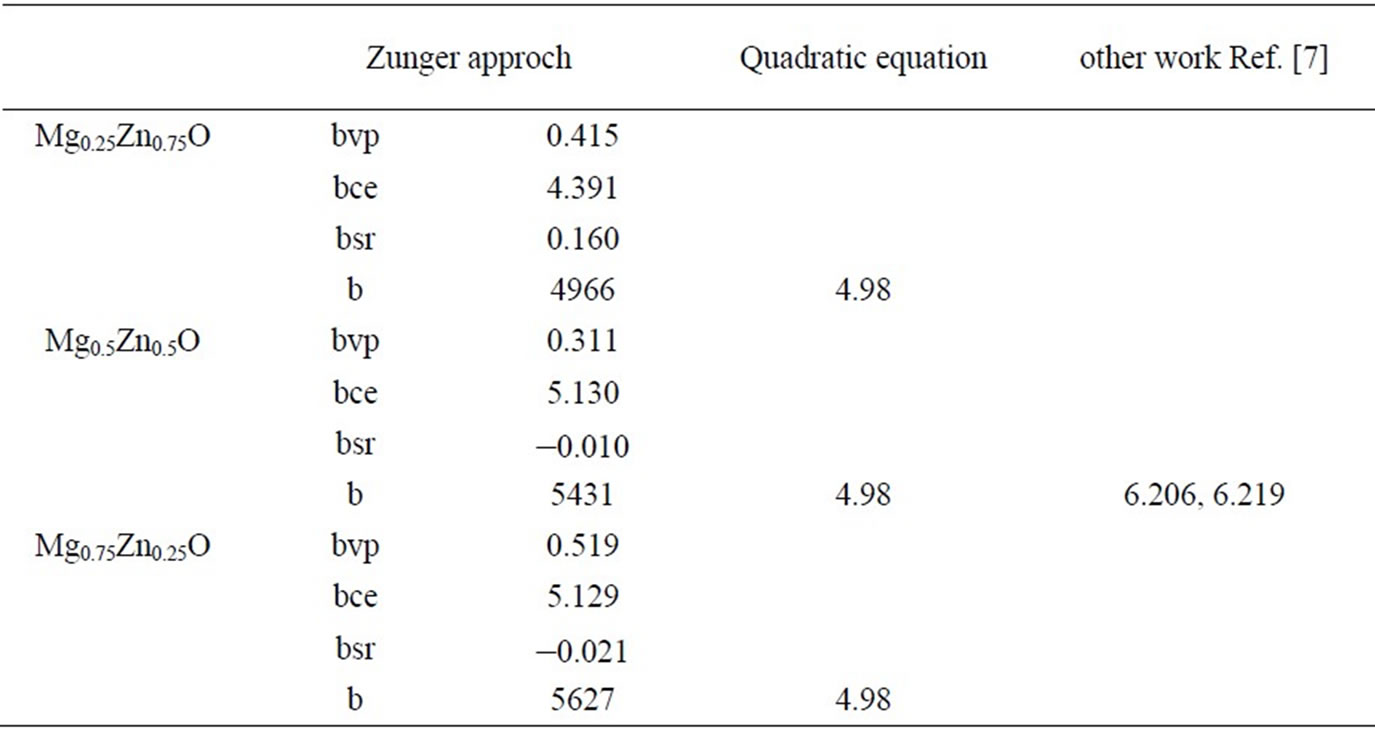
Table 5. Decomposition of optical bowing into volume deformation (VD), charge exchange (CE) and structural relaxation (SR). Contribution compared with the optical bowing obtained by a quadratic interpolation. (All valeurs are in eV).
REFERENCES
- X. Liu and J. K. Furdyna, “Optical Dispersion of Ternary II-VI Semiconductors Alloys,” Journal of Applied Physics, Vol. 95, No. 12, 2004, pp. 7754-7764. doi:10.1063/1.1739291
- Y. Z. Zhu, G. D. Chen and H. G. Ye, “Electronic Structure and Phase Stability of MgO, ZnO, CdO and Related Ternary Alloys,” Physical Review B, Vol. 77, No. 24, 2008, pp. 245209-245217.
- J. Chen, W. Z. Shen, N. B. Chen, D. J. Qiu and H. Z. Wu, “The Study of Composition Non-Uniformity in Ternary MgxZn1-xO Thin Films,” Journal of Physics: Condensed Matter, Vol. 15, No. 30, 2003, pp. 475-482. doi:10.1088/0953-8984/15/30/102
- F. El H. Hassan and H. Akbarzadeh, “First Principles Investigation of BNxP1-x, BNxAs1-x and BPxAs1-x Ternary Alloys,” Materials Science & Engineering B, Vol. 121, No. 1-2, 2005, pp. 171-178.
- F. El H. Hassan, “Study of the Gap Bowing in BNxSb1-x, BPxSb1-x and BAxSb1-x Ternary Alloys,” Physica Status Solidi (B), Vol. 242, No. 15, 2005, pp. 3129-3137. doi:10.1002/pssb.200441157
- D. Fritsh, H. Schmidt and M. Grundmann, “Pseudopotential Band Structures of Rocksalt MgO, ZnO and Mg1-x ZnxO,” Applied Physics Letters, Vol. 88, No. 13, 2006, pp. 134104-134106. doi:10.1063/1.2188382
- B. Amrani, R. Ahmed and F. El H. Hassan, “Structural, Electronic and Thermodynamic Properties of Wide Band Gap MgxZn1-xO Alloy,” Computational Materials Sciences, Vol. 40, No. 1, 2007, pp. 66-72. doi:10.1016/j.commatsci.2006.11.001
- B. Abidri, M. Rabah, D. Rached and H. Baltache, “Full Potential Calculation of Structural, Elastic Properties and High-Pressure Phase of Binary Noble Metal Carbide: Ruthenium Carbide,” Journal of Physics and Chemistry of Solids, Vol. 71, No. 12, 2010, pp. 1780-1784. doi:10.1016/j.jpcs.2010.09.014
- F. Badi, S. Louhibi, M. R. Aced, N. Mehnane and N. Sekkal, “Investigation of the Structural and Electronic Properties of Quantum well Superlattices made of CuCl, CuBr and CuI,” Physica E: Low-Dimensional Systems and Nanostructures, Vol. 41, No. 1, 2008, pp. 45-49. doi:10.1016/j.physe.2008.05.022
- M. Ameri, D. Rached, M. Rabah and R. Khenata, “Structural and Electronic Properties Calculations of BexZn1-xSe Alloy,” Materials Sciences in Semiconductor Processing, Vol. 10, No. 1, 2007, pp. 6-13. doi:10.1016/j.mssp.2007.01.003
- S. Savrasov and D. Savrasov, “Full Potential Linear Muffin-Tin Orbital Method for Calculating Total Energies and Forces,” Physical Review B, Vol. 46, No 19, 1992, pp. 12181-12195. doi:10.1103/PhysRevB.46.12181
- 2007. http:// www.physics.ucdavis.edu/_savrasov/S
- J. P. Perdew and Y. Wang, “Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy,” Physical Review B, Vol. 45, No. 13, 1992, pp. 13244-13249. doi:10.1103/PhysRevB.45.13244
- P. Blochl, O. Jepsen and O. K. Andersen, “Improved Tetrahedron Method for Brillouin Zone Integrations,” Physical Review B, Vol. 49, No. 23, 1994, pp. 16223-16233. doi:10.1103/PhysRevB.49.16223
- A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernad, “Special Quasirandom Structures,” Physical Review Letters, Vol. 65, No. 3, 1990, pp. 353-356. doi:10.1103/PhysRevLett.65.353
- Z. Charifi, F. El H. Hassan, H. Baaziz, S. Khosravizadeh, S. J. Hashemifar and H. Akbarzadeh, “Structural and Electronic Properties of the Wide-Gap Zn1-xMgxS, Zn1-xMgxSe and Zn1-xMgxTe Ternary Alloys,” Journal of Physics: Condensed Matter, Vol. 17, No. 14, 2005, pp. 7077-7088. doi:10.1088/0953-8984/17/44/001
- F. El H. Hassan, B. Amrani and F. Bahsoun, “Ab Initio Investigations of Zinc Chalcogenides Semiconductor Alloys,” Physica B: Condensed Matter, Vol. 391, No. 2, 2007, pp. 363-370. doi:10.1016/j.physb.2006.10.020
- H. Baaziz, Z. Charifi, F. El H. Hassan, S. J. Hashmifar and H. Akbarzadeh, “FP-LAPW Investigations of Zn1-x BexS, Zn1-xBexSe and Zn1-xBexTe Ternary Alloys,” Physica Status Solidi (B), Vol. 243, No. 6, 2006, pp. 1296- 1305. doi:10.1002/pssb.200541481
- B. Amrani, F. El H. Hassan and M. Zoeter, “First-Principles Study of Rocksalt AgClxBr1-x Alloys,” Physica B: Condensed Matter, Vol. 396, No. 1-2, 2007, pp. 192-198. doi:10.1016/j.physb.2007.04.004
- B. Amrani, F. El H. Hassan, R. Khenata and H. Akbarzadeh “Theoretical Study of CuxAg1-xI Alloys,” Journal of Physics and Chemistry of Solids, Vol. 70, No. 7, 2009, pp. 1055-1061. doi:10.1016/j.jpcs.2009.05.003
- S. Labidi, M. Labidi, H. Meradji, S. Ghemid, F. El H. Hassan, “Structural, Electronic, Thermodynamic and Optical Properties of SrS1-xOx Mixed Crystals,” Physica B: Condensed Matter, Vol. 404, No. 21, 2009, pp. 4100- 4105. doi:10.1016/j.physb.2009.07.168
- G. P. Srivastava, J. L. Martins and A. Zunger, “Atomic Structure and Ordering in Semiconductor Alloys,” Physical Review B, Vol. 31, No. 4, 1985, pp. 2561-2564. doi:10.1103/PhysRevB.31.2561
- F. D. Murnaghan, “The Compressibility of Media under Extreme Pressures,” Proceedings of the National Academy of Sciences USA, Vol. 30, 1994, pp. 244-247.
- L. Vegard, “Formation of Mixed Crystals by Solid-Phase Contact,” Journal of Physics, Vol. 5, No 5, 1921, pp. 393- 395.
- J. E. Bernard and A. Zunger, “Optical Bowing in Zinc Chalcogenide Semiconductor Alloys,” Physical Review B, Vol. 34, No. 8, 1986, pp. 5992-5995. doi:10.1103/PhysRevB.34.5992
- S. Desgreniers, “High Density Phases of ZnO: Structural and Compressive Parameters,” Physical Review B, Vol. 58, No. 21, 1998, pp. 14102-14105. doi:10.1103/PhysRevB.58.14102
- H. Karzel, W. Potzel, M. Kofferlein and W. Schiessl, “Lattice Dynamics and Hyperfine Interactions in ZnO and ZnSe at High External Pressures,” Physical Review B, Vol. 53, No. 17, 1996, pp. 11425-11438. doi:10.1103/PhysRevB.53.11425
- J. E. Jaffe, J. A. Snyder, Z. Lin and A. C. Hess, “LDA and GGA Calculations for High-Pressure Phase Transitions in ZnO and MgO,” Physical Review B, Vol. 62, No. 1, 2000, pp. 1660-1665.
- B. Amrani, I. Chhiboub, S. Hiadsi, T. Benmessabih and N. Hamdadou, “Structural and Electronic Properties of ZnO under High Pressures,” Solid State Communications, Vol. 137, No. 7, 2006, pp. 395-399. doi:10.1016/j.ssc.2005.12.020
- Y. Fei, “Effets of Temperature and Composition on the Bulk Modulus of (Mg, Fe)O,” American Mineralogist, Vol. 84, 1999, pp. 272-276.
- S. Spezial, C. S. Zha, T. S. Duffy and R. J. Hemley, “Quasi-Hydrostatic Compression of Magnesium Oxide to 52 GPa: Implication for the Pressure-Volume-Temperature Equation of State,” Journal of Geophysical Research, 106, No. B1, 2001, pp. 515-528.
- T. Tsuchiya and K. Kawamura, “Systematics of Elasticity: Ab Initio Study in B1-Type Alkaline Earth Oxides,” Journal of Chemical Physics, Vol. 114, No. 22, 2001, pp. 10086-10093. doi:10.1063/1.1371498
- H. K. Mao and P. M. Bell, “Equation of State of MgO and Fe under Static Pressure Conditions,” Journal of Geophysical Research Solid Earth, Vol. 84, No. B9, 1979, pp. 4533-4536. doi:10.1029/JB084iB09p04533
- A. Segura, J. A. Sans, F. J. Manjon, A. Munoz and M. J. Herrera-Cabrera, “Optical Properties and Electronic Structure of Rocksalt ZnO under Pressure,” Applied Physics Letters, Vol. 83, No. 2, 2003, pp. 278-280. doi:10.1063/1.1591995
- R. C. Whited, C. J. Flaten and W. C. Walker, “Exciton Thermoreflectance of MgO and CaO,” Solid State Communications, Vol. 13, No. 11, 1973, pp. 1903-1905. doi:10.1016/0038-1098(73)90754-0
- V. S. Stypanyuk, A. Szasz and B. L. Grigorenko, “Electronic Structure and Optical Properties of MgO Band Structure Calculation and Cluster Model,” Physica Status Solidi (B), Vol. 155, No. 1, 1989, pp. 179-184. doi:10.1002/pssb.2221550116

