Modeling and Numerical Simulation of Material Science
Vol.2 No.2(2012), Article ID:18406,6 pages DOI:10.4236/mnsms.2012.22004
Enhancement of Ferromagnetic Ordering Curie Temperature in N-Doped MgO under Hydrostatic Pressure
1Modelling and Simulation in Materials Science Laboratory, Djillali Liabès University of Sidi Bel-Abbès, Sidi Bel-Abbès, Algeria
2Signals and Systems Laboratory, Abdelhamid Ibn Badis University of Mostaganem, Mostaganem, Algeria
3Elaboration Characterization Physico-Mechanics of Materials and Metallurgical Laboratory ECP3M, Faculty of Sciences and Technology, Abdelhamid Ibn Badis University of Mostaganem, Mostaganem, Algeria
Email: ali_zaoui@yahoo.fr
Received December 8, 2011; revised January 15, 2012; accepted February 13, 2012
Keywords: APW + lo Method; Impurity Defects; Ferromagnetic Semiconductor
ABSTRACT
We have explored the magnetic properties of Nitrogen doped cubic MgO using the full potential linearized augmented plane wave (FP-LAPW) method. The unit cell has 128 atoms, and two Nitrogen atoms are placed in the positions of oxygen sites. This corresponds to 3.125% doping concentration. Our calculations predict that the ferromagnetic state, with a magnetic moment of about 1.0 μB per Nitrogen-dopant, is more favorable in energy than the nonmagnetic state, and the ferromagnetic correlations are influenced by the impurity bound state. The magnetic moment mainly arises from p orbital of Nitrogen which substitutes the Oxygen atom, with a little contribution from the Oxygen atoms surrounding Nitrogen atom. The resulting band structure and densities of states agree well with the recent theoretical works. The ferromagnetic ordering temperatures obtained from DFT simulations have been given in detail. Our results show that the pressure enhances the temperature in MgO:N.
1. Introduction
Very recently, several studies of ferromagnetism in nonmagnetic oxide semiconductors doped with nonmagnetic element have proved that the moments induced in the p orbitals of oxygen band are responsible for magnetism in these systems instead of the partially filled d orbitals [1- 4]. So, the substitution of oxygen with 2p light elements in d0 dilute magnetic semiconductors, such as Cor N impurities, gives rise to a magnetic polarization of valence states. Moreover, experiments and computations predicted that these systems become ferromagnetic (FM) when doped with C or N atoms [5-6]. All observation indicate that the substitution of nitrogen for oxygen in MgO can produce holes in N 2p orbitals with local magnetic moments, which may form a ferromagnetic order. In particular, considerable works have been devoted to the study of MgO doped with nitrogen where the ferromagnetism has been confirmed and other electronic and magnetic properties have been also discussed [7-14]. The experimental claims for d0 ferromagnetism are numerous and include graphitic carbon [15] and both defective [16] and doped oxides [17]. An explanation of these findings however remains controversial to date. The formation of the magnetic moment is usually attributed to holes localized at the defect site, either this being the molecular orbital associated to cation vacancies [1,2] or p-dopants at the O sites. [3,18] The application of hydrostatic pressure as an external control parameter to modify the different band parameters and the local magnetic exchange interaction contributes to the coherent understanding of the origin of ferromagnetism in MgO:N compound. The corresponding changes in the local exchange interactions with magnetic impurities provide detailed information about the nature of the underlying mechanisms that are responsible for the observed macroscopic magnetization. The ferromagnetic ordering temperature TC of MgO doped with nitrogen is below 5 K in the bulk limiting its applications [4]. It has been proven that, in several works, the biaxial and hydrostatic pressure [19- 22] significantly increases TC toward room temperature. For example, EuS reaches TC = 290 K at P = 88 GPa [19]. To date, some theoretical studies have been carried out [7-14] to explore the electronic structure of N-doped MgO. However, there have been no theoretical studies performed on the magnetic properties of N-doped MgO under hydrostatic pressure. In this work, we investigate the evolution of the ferromagnetic and the Curie temperature under pressure, and understand the mechanism of the magnetism in the nonmagnetic impurity N-doped MgO. Our investigation is significant for understanding of the nature of magnetism of Oxides semiconductors by substituting nitrogen for Oxygen. The paper has been organized as follows. In Section 2, we describe the computational approach adopted. Section 3, Results and Discussion, has been divided into two subsections dedicated to magnetic and electronic structure of MgO:N, and pressure dependence of the Curie temperatures in MgO doped 2p-N. The conclusions are summarized in the last section (Section 4).
2. Computational Details
The calculations have been performed within DFT implemented in the WIEN2k code [23]. Atoms were represented by hybrid full-potential (linear) augmented planewave plus local orbitals (L/APW + lo) method [24]. In this method, wave functions, charge density, and potential are expanded in spherical harmonics within no overlapping muffin-tin spheres, and plane waves are used in the remaining interstitial region of the unit cell. In the code, the core and valence states are treated differently. Core states are treated within a multiconfiguration relativistic Dirac-Fock approach, while valence states are treated in a scalar relativistic approach. The exchangecorrelation energy was calculated using the PerdewWang local density approximations (LDA) [25]. Very carefully step analysis is done to ensure convergence of the total energy in terms of the variational cutoff-energy parameter. At the same time we have used an appropriate set of k points to compute the total energy. We compute equilibrium lattice constants and bulk moduli by fitting the total energy versus volume to the Murnaghan equation [26]. The total energy was minimized using a set of 10 k-points in the irreducible sector of Brillouin zone, equivalent to a 5 × 5 × 5 Monkhorst-Pack [27] grid in the unit cell, and the value of 7 Ry for the cutoff energy were used. The self-consistent calculations are considered to be converged only when the calculated total energy of the crystal converged to less than 1 mRy. We have adopted the values of 2.5 bohr for Mg, 1.6 bohr for O, and 1.6 bohr for N, as MT radii. Density of states has been calculated with the 8 × 8 × 8 k-point mesh and using the linear tetrahedron method with Blöchl corrections [28]. N impurities have been studied by performing supercell calculations. Here substitutional defects are considered. The supercell is made by multiples of the lattice vectors a, b, c, like the 4 × 4 × 4 supercell (128-atoms) for the cubic phase, and two N ions in the O sites were substituted taking the following positions: (1/2, 3/8, 1/4) and (1/2, 7/8, 1/4). With this construction a substitution of Mg64O62N2 for the cubic phase of MgO was done. We have given careful consideration to 128-atoms supercell with double N impurities for the three magnetic states: nonmagnetic (NM), ferromagnetic (FM) and anti-ferromagnetic (AFM).
3. Results and Discussion
3.1. Magnetic and Electronic Structure of MgO:N
For the zero-pressure, our calculation total-energy shows that the magnetic moments of the two N dopant atoms, which are separated by dN-N = 8.3467 Å, favor FM coupling and its energy is lower than that of the corresponding anti-ferromagnetic (AFM) state. We start our analysis by briefly comparing the ground state of the MgO compound. The pure compound crystallizes in the rock-salt structure with a lattice parameter of 4.21 [29] Å and exhibits a wide band gap of 7.8 eV [30]. In our density-functional calculations the lattice parameter and gap are found to be 4.16 Å and 5 eV respectively due to the well-known underestimation of insulator band gaps within local density functional theory. Next, we discuss in details the electronic structure of a cubic MgO:N. The LSDA band structure and partial density of state (PDOS) calculated at the equilibrium lattice constant of 4.18 Å are displayed in Figure 1. These results reveal the halfmetallic character of Mg64O62N2 with a direct gap of 4.31 eV at the G point in the majority spin channel; on the other hand, the N-2p states overlap significantly with those of O-2p near the Fermi level, suggesting a strong interaction between them which results in the splitting of the energy levels near the Fermi energy. The spin-up states are fully occupied but spin-down states are partially filled. Our magnetic moment results are found about ~2.0760 μB (~0.9303 μB from N itself, ~0.2264 μB from its six first neighboring O atoms, and ~0.0789 μB from its six nearest neighboring Mg atoms) which are in an excellent agreement with other theoretical data [8-10,14]. The corresponding charge density and spin-density distribution in (100) plane is shown in Figure 2. The majority of magnetic moments reside on the 2p states of anionic nitrogen and its neighboring anionic oxygen. From Figure 2, it is clear that the N atom is the main contributor to the magnetic moment, and the four neighboring O atoms are also slightly polarized. Therefore, the magnetic moment in N-doped MgO is mainly contributed by the anions, and it is resulted mainly from the localized 2p orbitals. Figure 2 indicates clearly that this compound has mixed bonding nature. Two nitrogen atoms form a very strong covalent bond. We can see some electrons between the metallic and oxygen/nitrogen atoms, this is witness of a strong directional bond that exists between them, indicating the covalent bond in MgO:N. When the

Figure 1. Electronic structure of MgO:N with LSDA approach.
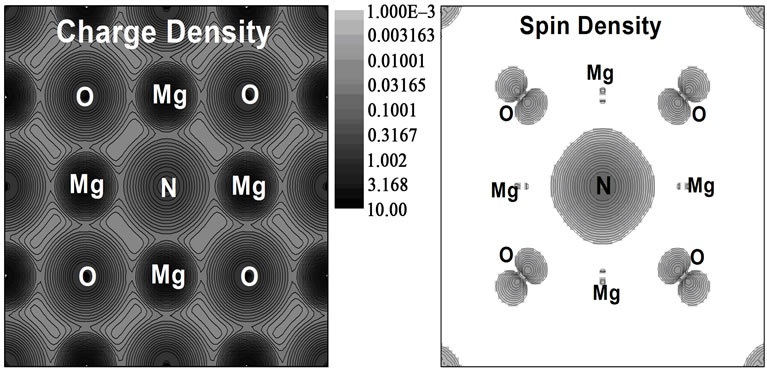
Figure 2. Total electron density and spin density contours of MgO:N in (100) plane using LSDA approach.
large electronegativity difference between Mg and O (N) has been considered, we conclude that there is an ionic bonding between Mg and O (N). It can be seen that for our material there is an increase in electron charge distribution at the O and N sites, and a net decrease in the Mg sites. Till now, all calculated properties are in well agreement with other theoretical and experiment works [7-14]. Our aim is not to compare and discuss these confirmed results but to examine it under hydrostatic pressure. The application of hydrostatic pressure as an external control parameter to modify the different band parameters and the local magnetic exchange interaction contributes to the coherent understanding of the origin of ferromagnetism and its impact on various electronic phenomena in this compound.
3.2. Pressure Dependence of the Curie Temperatures in MgO Doped 2p-N
The application of hydrostatic pressure serves as a unique tool for tuning the different lattice constant dependent parameters in solids. The corresponding changes in the extended band states as well as in the local exchange interactions with nonmagnetic impurities provide detailed information about the nature of the underlying mechanisms that are responsible for the observed macroscopic magnetization.
The partial densities of state of 2p-N and 2p-O at normal and under hydrostatic pressure are shown in Figure 3. We notice that our results are very similar by varying the pressure; where these two states always dominate at the vicinity of the Fermi level. The only difference between all the shown densities of states is that the oxygen valence band becomes wider when pressure is applied. Consequently, the half metallic character is observed as well as the ferromagnetic order.
We have also estimated the Curie temperatures of MgO:N based on the mean-field theory and Heisenberg model [31,32] (kBTC = 2Emag/3). Here Emag is the magnetic energy (energy difference between FM and AFM coupling) obtained from our first-principles calculations.
To better visualize the behavior of Curie temperatures under hydrostatic pressure, to analyze the evolution of the magnetic energy, and to explain what causes these trends, we have traced all parameters such as ∆E, interatomic distance, magnetic moment, and Curie temperature in Figure 4. For a smaller than 4.18 Å until p = 250 GPa with the inter-atomic distance between two N atoms dN-N = 7.1501 Å, the magnetic moment becomes constant and the material keeps its ferromagnetic state (see Figures 4(a)-(c)). It can be seen that the energy difference Emag (AFM-FM) increases under hydrostatic pressure since the 2p orbitals are responsible to the strengthening of the FM exchange interactions in electronic structure of our system. This proves that our Mg64O62N2 system favors FM alignment than that of the corresponding antiferromagnetic (AFM) state. So, the increase in Curie temperature is justified by the increase in Emag because they are proportionals in the above equation. Our calculations have shown that the application of 250 GPa hy-

Figure 3. Partial densities of state of 2p-N and 2p-O at normal and under hydrostatic pressure.
drostatic pressure leads to a remarkable enhancement of the Curie temperatures (up to 100%), and it is found to be about 44 K.
4. Conclusion
In conclusion, an ab initio study of the electronic structure under hydrostatic pressure of N doped MgO has been conducted in order to understand the origin of magnetism. The MgO:N compound in which Oxygen is substituted by Nitrogen atoms is found to be ferromagnetic for all pressures estimated. The N atom forms a partially occupied gap state at the vicinity of the valence band edge which makes this material half metallic. It is found that the doping of N results a strong coupling between 2p states of dopant (N) and host (O). Finally, our calcula-
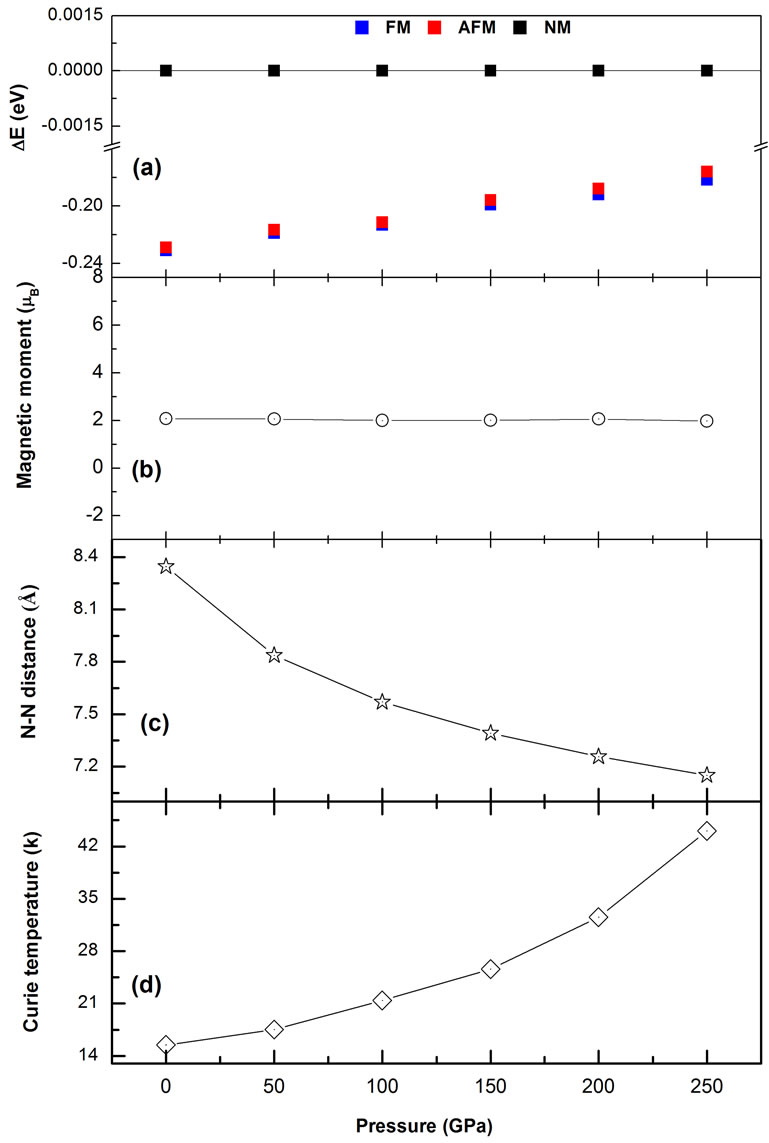
Figure 4. Magnetic phase stability, spin magnetic moments, inter-atomic distance, and Curie temperature vs the pressure in MgO:N compound.
tions show that the Curie temperature TC increases with hydrostatic pressure and it is found to be about 44 K for 250 GPa pressure.
REFERENCES
- S. Elfimov, S. Yunoki and G. A. Sawatzky, “Possible Path to a New Class of Ferromagnetic and Half-Metallic Ferromagnetic Materials,” Physical Review Letters, Vol. 89, No. 21, 2002, pp. 216403-216406. doi:10.1103/PhysRevLett.89.216403
- C. D. Pemmaraju and S. Sanvito, “Ferromagnetism Driven by Intrinsic Point Defects in HfO2,” Physical Review Letters, Vol. 94, No. 21, 2005, pp. 217205-217208. doi:10.1103/PhysRevLett.94.217205
- I. S. Elfimov, A. Rusydi, S. I. Csiszar, Z. Hu, H. H. Hsieh, H.-J. Lin, C. T. Chen, R. Liang and G. A. Sawatzky, “Magnetizing Oxides by Substituting Nitrogen for Oxygen,” Physical Review Letters, Vol. 98, No. 13, 2007, pp. 137202-137205. doi:10.1103/PhysRevLett.98.137202
- V. Pardo and W. E. Pickett, “Magnetism from 2p States in Alkaline Earth Monoxides: Trends with Varying N Impurity Concentration,” Physical Review B, Vol. 78, No. 13, 2008, pp. 134427-134431. doi:10.1103/PhysRevB.78.134427
- K. Kenmochi, M. Seike, K. Sato, A. Yanase and H. Katayama-Yoshida, “A New Class of Diluted Ferromagnetic Semiconductors Based on CaO without Transition Metal Elements,” Japanese Journal of Applied Physics, Vol. 43, No. 7A, 2004, pp. 934-936. doi:10.1143/JJAP.43.L934
- K. Kenmochi, V. A. Dinh, K. Sato, A. Yanase and H. Katayama-Yoshida, “Materials Design of Transparent and Half-Metallic Ferromagnets of MgO, SrO and BaO without Magnetic Elements,” Journal of the Physical Society of Japan, Vol. 73, No. 11, 2004, pp. 2952-2954. doi:10.1143/JPSJ.73.2952
- V. Sharma and J. E. Lowther, “Ferromagnetism in Nitrogen Doped Magnesium Oxide: A First Principle Study,” Journal of Nanoand Electronic Physics, Vol. 3, No. 1, 2011, pp. 453-459.
- B. Gu, N. Bulut, T. Ziman and S. Maekawa, “Possible d0 Ferromagnetism in MgO Doped with Nitrogen,” Physical Review B, Vol. 79, No. 2, 2008, pp. 024407-024413. doi:10.1103/PhysRevB.79.024407
- H. Wu, A. Stroppa, S. Sakong, S. Picozzi, M. Scheffler and P. Kratzer, “Magnetism in Cor N-doped MgO and ZnO: A Density-Functional Study of Impurity Pairs,” Physical Review Letters, Vol. 105, No. 26, 2010, pp. 267203-267206. doi:10.1103/PhysRevLett.105.267203
- M. Pesci, F. Gallino, C. D. Valentin and G. Pacchioni, “Nature of Defect States in Nitrogen-Doped MgO,” Journal of Physical Chemistry C, Vol. 114, No. 2, 2010, pp. 1350-1356. doi:10.1021/jp9097556
- J. M. D. Coey, “d0 Ferromagnetism,” Solid State Sciences, Vol. 7, No. 6, 2005, pp. 660-667. doi:10.1016/j.solidstatesciences.2004.11.012
- J. I. Beltrán, C. Monty, Ll. Balcells and C. Martínez-Boubeta, “Possible d0 Ferromagnetism in MgO,” Solid State Communications, Vol. 149, No. 39-40, 2009, pp. 1654-1657. doi:10.1016/j.ssc.2009.06.044
- K. S. Yang, R. Q. Wu, L. Shen, Y. P. Feng, Y. Dai and B. B. Huang, “Origin of d0 Magnetism in II-VI and III-V Semiconductors by Substitutional Doping at Anion Site,” Physical Review B, Vol. 81, No. 12, 2010, pp. 125211- 125215. doi:10.1103/PhysRevB.81.125211
- A. Droghetti, C. D. Pemmaraju and S. Sanvito, “Predicting d0 Magnetism: Self-Interaction Correction Scheme,” Physical Review B, Vol. 78, No. 14, 2008, pp. 140404(R)- 140407(R). doi:10.1103/PhysRevB.78.140404
- T. Makarova and F. Palacio, “Carbon-Based Magnetism: An Overview of the Magnetism of Metal Free Carbon-Based Compounds and Materials,” Elsevier, Amsterdam, 2006.
- M. Venkatesan, C. B. Fitzgerald and J. M. D. Coey, “Thin Films: Unexpected Magnetism in a Dielectric Oxide,” Nature, Vol. 430, No. 7000, 2004, p. 630. doi:10.1038/430630a
- H. Pan, J. B. Yi, L. Shen, R. Q. Wu, J. H. Yang, J. Y. Lin, Y. P. Feng, J. Ding, L. H. Van and J. H. Yin, “RoomTemperature Ferromagnetism in Carbon-Doped ZnO,” Physical Review Letters, Vol. 99, No. 12, 2007, pp. 127201- 127204. doi:10.1103/PhysRevLett.99.127201
- G. Bouzerar and T. Ziman, “Model for Vacancy-Induced d0 Ferromagnetism in Oxide Compounds,” Physical Review Letters, Vol. 96, No. 20, 2006, pp. 207602-207605. doi:10.1103/PhysRevLett.96.207602
- N. M. Souza-Neto, D. Haskel, Y.-C. Tseng and G. Lapertot, “Pressure-Induced Electronic Mixing and Enhancement of Ferromagnetic Ordering in EuX (X = Te, Se, S, O) Magnetic Semiconductors,” Physical Review Letters, Vol. 102, No. 5, 2009, pp. 057206-057209. doi:10.1103/PhysRevLett.102.057206
- L. Bergqvist, B. Belhadji, S. Picozzi and P. H. Dederichs, “Volume Dependence of the Curie Temperatures in Diluted Magnetic Semiconductors,” Physical Review B, Vol. 77, No. 1, 2008, pp. 014418-014424. doi:10.1103/PhysRevB.77.014418
- I. N. Goncharenko and I. Mirebeau, “Ferromagnetic Interactions in EuS and EuSe Studied by Neutron Diffraction at Pressures up to 20.5 GPa,” Physical Review Letters, Vol. 80, No. 5, 1998, pp. 1082-1085. doi:10.1103/PhysRevLett.80.1082
- J. Kunes, W. Ku and W. E. Pickett, “Exchange Coupling in Eu Monochalcogenides from First Principles (Condensed Matter: Electronic Structure, Electrical, Magnetic and Optical Properties),” Journal of the Physical Society of Japan, Vol. 74, No. 5, 2005, pp. 1408-1411. doi:10.1143/JPSJ.74.1408
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz, “WIEN2k, An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties,” 2th Edition, Vienna University of Technology, Vienna, 2001.
- E. Sjöstedt, L. Nordstrom and D. J. Singh, “An Alternative Way of Linearizing the Augmented Plane-Wave Method,” Solid State Communication, Vol. 114, No. 1, 2000, pp. 15- 20. doi:10.1016/S0038-1098(99)00577-3
- J. P. Perdew and Y. Wang, “Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy,” Physical Review B, Vol. 45, No. 23, 1992, pp. 13244- 13249. doi:10.1103/PhysRevB.45.13244
- F. D. Murnaghan, “The Compressibility of Media under Extreme Pressures,” Proceedings of the National Academy of Sciences of USA, Vol. 30, 1944, pp. 244-247. doi:10.1073/pnas.30.9.244
- H. J. Monkhorst and J. D. Pack, “Special Points for Brillouin-Zone Integrations,” Physical Review B, Vol. 13, No. 12, 1976, pp. 5188-5192. doi:10.1103/PhysRevB.13.5188
- P. E. Blöchl, O. Jepsen and O. K. Anderson. “Improved Tetrahedron Method for Brillouin-Zone Integrations,” Physical Review B, Vol. 49, No. 23, 1994, pp. 16223- 16233. doi:10.1103/PhysRevB.49.16223
- S. Speziale, C.-S. Zha, T. S. Duffy, R. J. Hemley and H.-K. Mao, “Quasi-Hydrostatic Compression of Magnesium Oxide to 52 GPa: Implications for the PressureVolume-Temperature Equation of State,” Journal of Geophysical Research, Vol. 106, No. B1, 2001, pp. 515-528. doi:10.1029/2000JB900318
- R. C. Whited, C. J. Flaten and W. C. Walker, “Exciton Thermoreflectance of MgO and CaO,” Solid State Communication, Vol. 13, No. 11, 1973, pp. 1903-1905. doi:10.1016/0038-1098(73)90754-0
- J. Kudrnovský, I. Turek, V. Drchal, F. Máca, P. Weinberger and P. Bruno, “Exchange Interactions in III-V and Group-IV Diluted Magnetic Semiconductors,” Physical Review B, Vol. 69, No. 11, 2004, Article ID: 115208. doi:10.1103/PhysRevB.69.115208
- F. Máca, J. Kudrnovský, V. Drchal and G. Bouzerar, “Magnetism without Magnetic Impurities in ZrO2 Oxide,” Applied Physics Letters, Vol. 92, No. 18-20, 2008, pp. 212503-212505. doi:10.1063/1.293685

