American Journal of Industrial and Business Management
Vol.1 No.1(2011), Article ID:8064,10 pages DOI:10.4236/ajibm.2011.11003
On Improving Replenishment Lot Size of an Integrated Manufacturing System with Discontinuous Issuing Policy and Imperfect Rework
![]()
1OIT-Enterprise Applications, Rutgers University, Busch Campus, Piscataway, USA; 2University Department of Business Administration; 3Department of Finance, Chaoyang University of Technology, Taichung, Taiwan.
Email: chs@cyut.edu.tw
Received August 10th, 2011; revised September 14th, 2011; accepted September 2nd, 2011.
Keywords: Manufacturing Systems, Replenishment Lot Size, Discontinuous Issuing Policy, Random Defective Rate, Quality Assurance, Multi-Delivery
ABSTRACT
This paper proposes a cost reduction distribution policy for an integrated manufacturing system operating under quality assurance practice. We reexamine the problem studied by Chiu et al. [Numerical method for determination of the optimal lot size for a manufacturing system with discontinuous issuing policy and rework. International Journal for Numerical Methods in Biomedical Engineering, doi:10.1002/cnm.1369] and improve its replenishment lot-size solution in terms of lowering producer’s stock holding cost. Mathematical modeling and analysis is employed in this study and optimal replenishment lot size is derived. A numerical example is provided to show the practical usage of research result as well as to demonstrate significant savings in producer’s holding cost as compared to that in Chiu et al.
1. Introduction
This paper proposes a cost reduction distribution policy to improve the economic lot size solution of a manufacturing system with discontinuous issuing policy and imperfect rework [1]. In manufacturing sector, the economic production quantity (EPQ) model is commonly used to assist producers in determining the optimal production lot size that minimizes overall production-inventory costs [2-4]. EPQ model implicitly assumes that items produced are of perfect quality. But in real-life production systems, due to process deterioration or other factors, generation of defective items is inevitable. Hence, many studies have been carried out to enhance EPQ model by addressing the imperfect quality production issue [5-14]. Rosenblatt and Lee [11] proposed an EPQ model that deals with imperfect quality. They assumed that at some random point in time the process might shift from an in-control to an out-of-control state, and a fixed percentage of defective items are produced. Approximate solutions for obtaining an optimal lot size were developed. Zhang and Gerchak [14] considered joint lot sizing and inspection policy in an EOQ model with random yield. Defective items sometimes can be reworked and repaired, and hence overall production costs can be significantly reduced [15-21]. Examples for such production processes may include printed circuit board assembly, or plastic injection molding, etc., sometimes employs rework as an acceptable process in terms of level of quality. Chiu et al. [17] studied the optimal replenishment policy for manufacturing systems with failure in rework, backlogging, and random breakdown. Grosfeld-Nir and Gerchak [18] considered multistage production systems where defective units can be reworked repeatedly at every stage. They showed that a multistage system where only one of the stages requires a set-up can be reduced to a single-stage system, and proved that it is best to make the “bottle-neck” the first stage of the system. They also developed recursive algorithms for solving twoand three-stage systems.
Another unrealistic assumption of classic EPQ model is the continuous inventory issuing policy for satisfying product demand. In real-life vendor-buyer integrated production-inventory system, multiple or periodic deliveries of finished products are commonly used. Schwarz [22] examined a one-warehouse N-retailer deterministic inventory system. The objective was to determine the stocking policy which minimizes average system cost per unit time. Necessary properties of an optimal policy were derived and the optimal solutions for the one-retailer and N identical retailer problems were given. Heuristic solutions for the general problem were also suggested, tested against analytical lower bounds and on the basis of these tests, found to be near optimal. Goyal [23] studied the integrated inventory model for the single supplier-single customer problem. He proposed a method that is typically applicable to those inventory problems where a product is procured by a single customer from a single supplier. An example was provided to illustrate his proposed method. Many studies have since been carried out to address various aspects of supply chain optimization [1,24-35]. Examples of these studies are surveyed as follows. Goyal and Nebebe [28] determined the economic production and shipment policy of a product supplied by a vendor to a single buyer. The objective of their study was to minimize the total joint annual costs incurred by the vendor and the buyer. Buscher and Lindner [26] presented a lot size model which addresses a production system with rework and equal sized batch shipments. Based on total relevant costs per unit time, an optimization method was developed to determine the economic production and rework quantity as well as the corresponding batch sizes for both activities. The algorithm was illustrated by a numerical example followed by a sensitivity analysis of the models behavior under different problem parameters. Diponegoro and Sarker [27] studied an ordering policy for raw materials as well as an economic batch size for finished products that are delivered to customers frequently at a fixed interval of time for a finite planning horizon. The problem was then extended to compensate for the lost sales of finished products. A closed-form solution to the problem was obtained for the minimal total cost. A lower bound on the optimal solution was also developed for problem with lost sale. It was shown that the solution and the lower bound were consistently tight. Hill [29] studied a model in which a manufacturing company purchases a raw material, manufactures a product (at a finite rate) and ships a fixed quantity of the product to a single customer at fixed and regular intervals of time, as specified by the customers, while minimizing total cost of purchasing, manufacturing and stockholding. Ojha et al. [31] studied a production system which receives raw material from a supplier, processes it, and delivers it to the customer periodically. They considered constant defective rate and defectives have to be reworked and the whole lot is quality-checked prior delivery within the cycle. Three scenarios were examined and the total cost equations were developed and evaluated separately for each model. Sarker and Khan [33] addressed the problem of a manufacturing system that procures raw materials from suppliers in a lot and processes them to convert to finished products. They proposed an ordering policy for raw materials to meet the requirements of a production facility. In turn, this facility must deliver finished products demanded by outside buyers at fixed interval points in time. A general cost model was developed first considering both raw materials and finished products. Then this model was used to develop a simple procedure to determine an optimal ordering policy for procurement of raw materials as well as the manufacturing batch size to minimize the total cost for meeting the customer demand on time. Chiu et al. [1] investigated the joint effect of a discontinuous inventory issuing policy and an imperfect rework process on the optimal replenishment lot size of an integrated EPQ model. They assumed that the random defective items produced are partially repairable and the rework process is not perfect either, scrap items may be generated during the rework. Fixed quantity multiple installments of the finished batch can only be delivered to customers if the whole lot is quality assured at the end of rework. A closed-form optimal lot size solution to the problem was obtained.
On improving the replenishment lot size solution derived by [1], this paper proposes a cost reduction distribution policy with the purpose of lowering producer’s stock holding cost. An n + 1 delivery policy is introduced here in lieu of n multi-delivery plan in [1]. The joint effects of the n + 1 multi-delivery policy and imperfect rework on the optimal replenishment lot size for this integrated EPQ model are studied.
2. Mathematical Modeling and Analysis
2.1. Model Description
Reexamine the specific EPQ model studied by Chiu et al. [1] which addressed two practical issues: the imperfect quality items produced and multi-delivery policy for transporting finished items. Assumptions of the model are as follow. Consider a manufacturing system which may produce x portion of random defective items at a production rate d. Among defective items, a θ portion is assumed to be scrap and the other (1 – θ) portion can be reworked and repaired at a rate P1, within the same cycle when regular production ends. A θ1 portion (where 0 θ1
θ1  1) of reworked items fails during the rework process and becomes scrap. Under the regular operating schedule, the constant production rate P is larger than the sum of demand rate λ and production rate of defective items d. That is: (P – d – λ) > 0; where d can be expressed as d = Px. Let d1 denote production rate of scrap items during the rework process, then d1 can be expressed as d1 = P1θ1. Under the proposed n + 1 delivery policy, an initial installment of finished (perfect quality) products is distributed to customer for satisfying the demand during producer’s production uptime and rework time. Then, at the end of rework, when the rest of the production lot is quality assured, fixed quantity n installments of finished items are delivered to customer at a fixed interval of time. Such an n + 1 delivery policy is intended to reduce supplier’s stock holding cost.
1) of reworked items fails during the rework process and becomes scrap. Under the regular operating schedule, the constant production rate P is larger than the sum of demand rate λ and production rate of defective items d. That is: (P – d – λ) > 0; where d can be expressed as d = Px. Let d1 denote production rate of scrap items during the rework process, then d1 can be expressed as d1 = P1θ1. Under the proposed n + 1 delivery policy, an initial installment of finished (perfect quality) products is distributed to customer for satisfying the demand during producer’s production uptime and rework time. Then, at the end of rework, when the rest of the production lot is quality assured, fixed quantity n installments of finished items are delivered to customer at a fixed interval of time. Such an n + 1 delivery policy is intended to reduce supplier’s stock holding cost.
The on-hand inventory of perfect quality items of the proposed model is depicted in Figure 1 (in black). The same for Chiu et al.’s model [1] is illustrated in red. One notes that the yellow/shade area indicates the expected reduction in manufacturer’s stock holding costs which benefit results from applying the proposed model.
The proposed system includes the following cost related parameters: setup cost K per production run, unit production cost C, unit holding cost h, unit rework cost CR, disposal cost per scrap item CS, holding cost h1 for each reworked item, fixed delivery cost K1 per shipment, and delivery cost CT per item shipped to customers. Other notations used also include:
T = cycle lengtht = the production time needed for producing enough perfect items for satisfying product demand during the production uptime t1 and the rework time t2t1 = the production uptime for the proposed EPQ modelt2 = time required for reworking of defective itemst3 = time required for delivering the remaining quality assured finished productsH = the level of on-hand inventory in units for satisfying product demand during manufacturer’s regular production time t1 and rework time t2H1 = maximum level of on-hand inventory in units when regular production endsH2 = the maximum level of on-hand inventory in units when rework process finishesQ = production lot size to be determined for each cycletn = a fixed interval of time between each installment of products delivered during t3n = number of fixed quantity installments of the rest of finished lot to be delivered during t3I(t) = on-hand inventory of perfect quality items at time tId(t) = on-hand inventory of defective items at time tIs(t) = on-hand inventory of scrap items at time tφ = overall scrap rate per cycle (sum of scrap rates in t1 and t2)TC(Q) = total production-inventory-delivery costs per cycle for the proposed modelE[TCU(Q)] = the long-run average costs per unit time for the proposed model.
2.2. Formulation and Derivation
From the assumption of the proposed model and Figure 1, one can derive the following expressions:
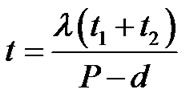 (1)
(1)
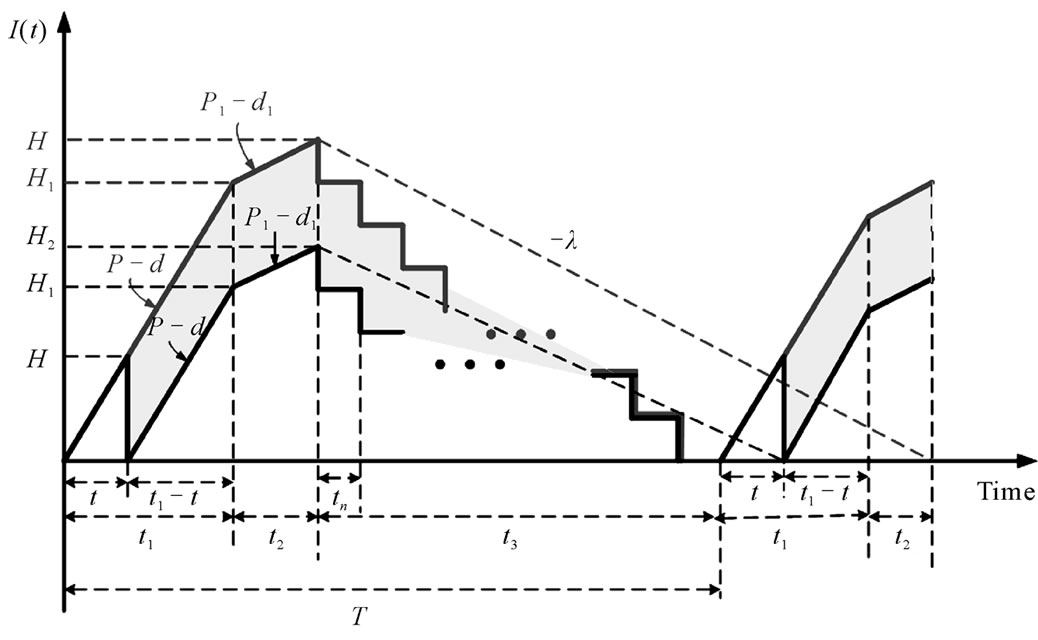
Figure 1. Expected reduction in producer’s stock holding costs (in yellow/shade) of the proposed model as compared to that in [1].
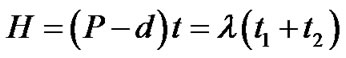 (2)
(2)
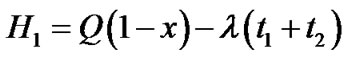 (3)
(3)
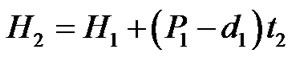 (4)
(4)
 (5)
(5)
 (6)
(6)
 (7)
(7)
It is noted that the maximum level of defective items is dt1. Among them a θ portion is scrap and the other (1 – θ) portion of defective items is considered to be re-workable. Time needed for reworking is shown in Equation (8). During the reworking, a portion θ1 of reworked items fail and becomes scrap. Figure 2 depicts the on-hand inventory of scrap items during t1 and t2. One notes that maximum level of scrap items during a cycle is φxQ (Equation (9)).
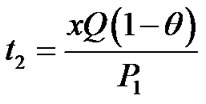 (8)
(8)
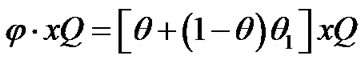 (9)
(9)
Total production-inventory-delivery costs per cycle TC(Q) consists of the variable production cost, the setup cost, variable rework cost, disposal cost, (n + 1) fixed distribution costs and variable delivery cost, holding cost for perfect quality items during production uptime t1 and reworking time t2, holding cost for defective items during t1, variable holding cost for items reworked during t2, and holding cost for finished goods during the delivery time t3 where n fixed-quantity installments of the finished
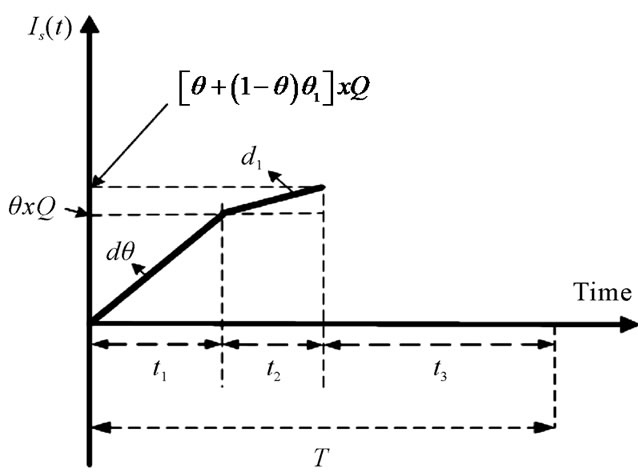
Figure 2. On-hand inventory of scrap items in the proposed mode with (n + 1) delivery policy and imperfect rework.
batch are delivered to customers at a fixed interval of time (one can refer to Appendix-2 of [1] for detailed computations).
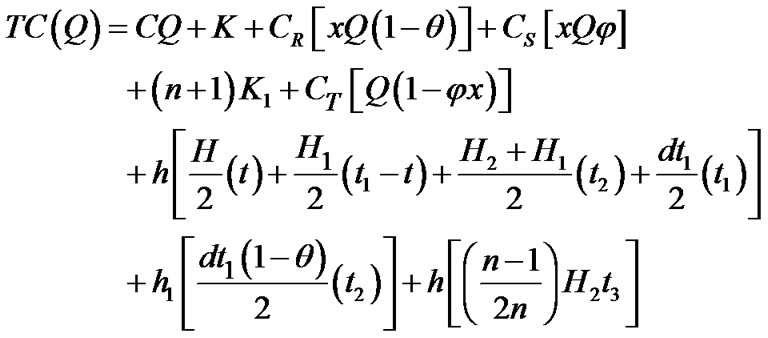 (10)
(10)
Taking into account of the randomness of defective rate x (which is assumed to be a random variable with a known probability density function), one can use the expected values of x in the related cost analysis. Substituting all related parameters from Equations (1) to (9) in TC(Q), one obtains the expected total E[TCU(Q)] as follows (see Appendix A for details).
 (11)
(11)
2.3. Proof of Convexity and Optimal Replenishment Lot Size
The optimal production lot size can be obtained by minimizing E[TCU(Q)]. Differentiating E[TCU(Q)] with respect to Q, the first and the second derivatives of E[TCU(Q)] are
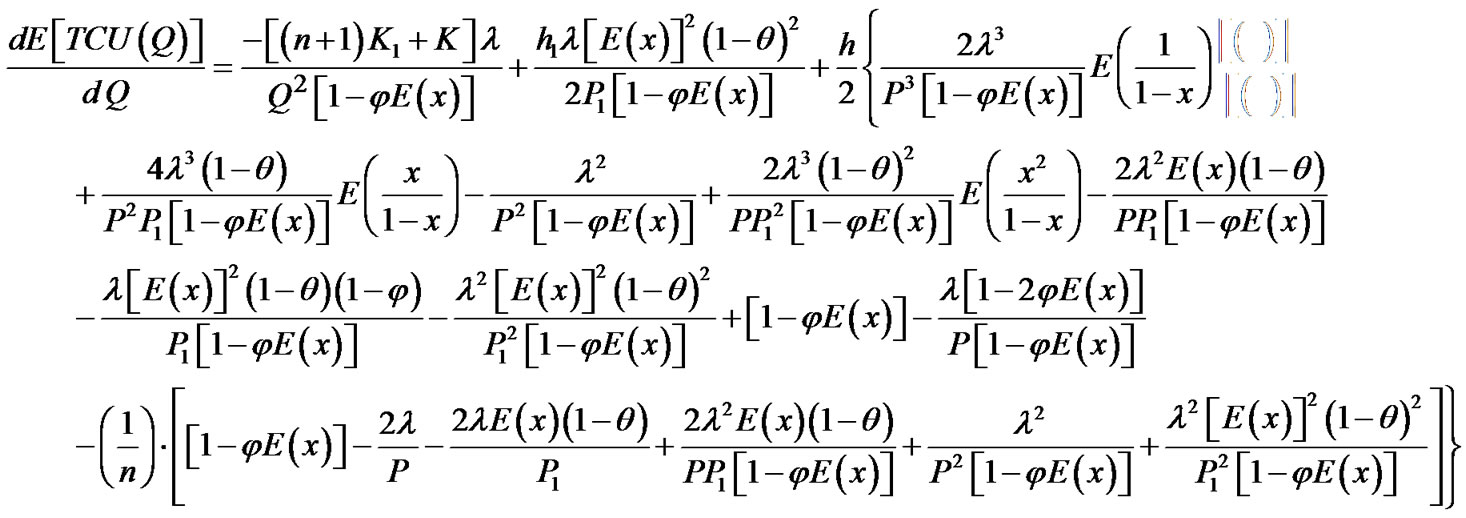 (12)
(12)
 (13)
(13)
The second derivative of E[TCU(Q)] is resulting positive, because K, n, K1, λ, Q, and (1 – φE[x]) are all positive. Hence, E[TCU(Q)] is convex, for all Q different from zero. Optimal lot size Q* can be obtained by setting the first derivative of E[TCU(Q)] equal to zero.
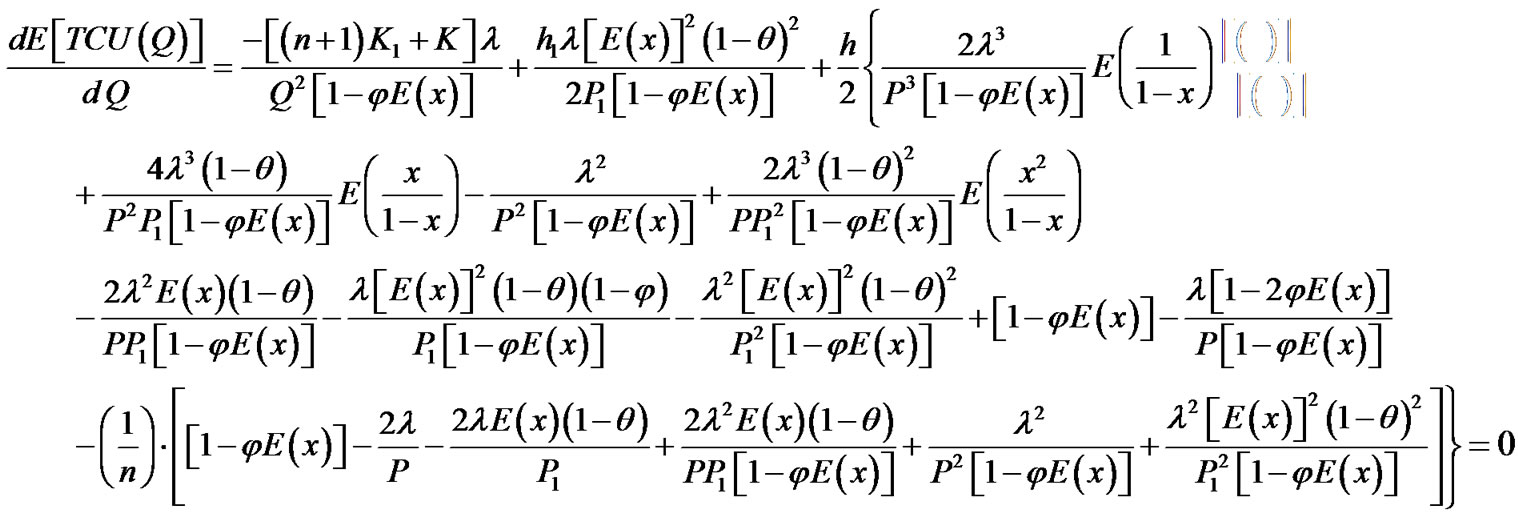 (14)
(14)
With further derivations, one obtains the optimal replenishment lot size as follows.
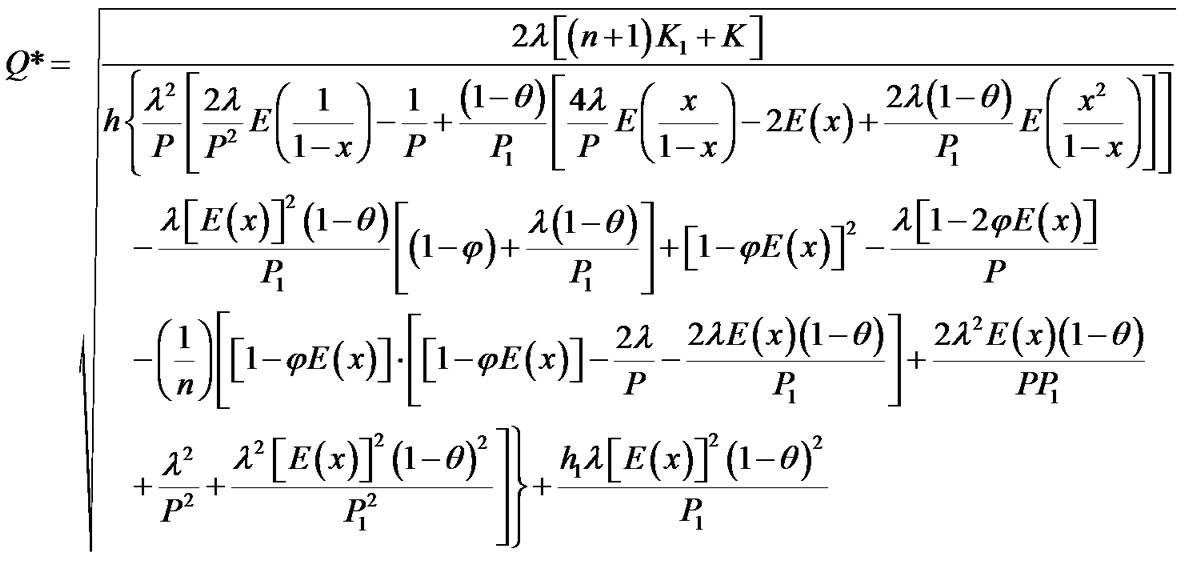 (15)
(15)
3. Numerical Example
With the purpose of comparison of the proposed model and Chiu et al.’s model [1], this section adopts the same numerical example as in [1]. Consider that a product can be manufactured at an annual rate of 60,000 units, and this item has a flat annual demand rate of 3,400 units. During production, a random defective rate x occurs and it is assumed to be uniformly distributed over interval [0, 0.3]. Among defective items a portion θ = 0.1 is considered to be scrap and the other portion is re-workable with a rate of rework P1 = 2,200 units per year. A θ1 = 0.1 portion of reworked items fails and becomes scrap during rework. Other parameters include: K = $20,000; C = $100 per item; CR = $60 per item reworked; CS = $20 per scrap item; h = $20; h1 = $40 per item reworked; a fixed cost K1 = $4,350 per shipment; and CT = $0.1 per item delivered.
In order to show practical usages of our research results, the following two different scenarios are demonstrated, respectively.
Scenario 1: Let total number of deliveries remain 4 (i.e. n = 4 as was used in [1]). For the proposed model, it is (n+1) = 4. An initial installment of finished products is distributed to customer during t1, for satisfying the product demand during producer’s production uptime and rework time. Then, at the end of rework, fixed quantity three other installments of finished items are delivered to customer at a fixed interval of time. Also, for the purpose of comparison, we use the lot-size solution Q = 3,553 (from [1]) in calculating the production-inventory-delivery cost (i.e. Equation (11) of the proposed model) and obtain E[TCU(3553)] = $442,990. One notes that there is a reduction in manufacturer holding costs amounts to $11,356 (see Figure 3), or 11.03% of total other related costs (i.e. E[TCU(Q)] – (λC): total cost excludes the variable production cost).
Scenario 2: Let total number of deliveries remain 4 (that is (n + 1) = 4 in our model). By applying Equations (15) and (11), one obtains the optimal replenishment lot size Q* = 4,271 and the expected total costs E[TCU(Q*)] = $441,949, respectively. It is noted that overall reducetion in production-inventory-delivery costs amounts to $12397, or 12.16% of total other related costs.
4. Concluding Remarks
Chiu et al. [1] studied the optimal lot size for a manufacturing system with discontinuous issuing policy and imperfect rework. They adopted an n multi-delivery plan which starts at the end of rework process when the entire lot is quality assured. With the purpose of reducing supplier’s stock holding cost, this paper extends Chiu et al.’s

Figure 3. Producer’s stock holding costs for the proposed (n + 1) delivery policy as compared to that in Chiu et al. [1].
model [1] and proposes an n + 1 delivery policy in lieu of their n multi-delivery plan. Mathematical modeling is employed and the expected integrated production-inventory-delivery cost function is derived and proved to be convex function. The closed-form optimal lot size solution to the problem is obtained. A numerical example is provided to show practical usage of our research result and demonstrate its significant savings in stock holding cost. For future research, one of the interesting and practical issues is to investigate effect of multiple customers on the lot size decision for the same model.
5. Acknowledgements
The authors greatly appreciate the support of National Science Council (NSC) of Taiwan under grant number: NSC 99-2410-H-324-007-MY3.
REFERENCES
- S. W. Chiu, K. -K. Chen and H. -D. Lin, “Numerical Method for Determination of the Optimal Lot Size for a Manufacturing System with Discontinuous Issuing Policy and Rework,” International Journal of Numerical Methods in Biomedical Engineering, Vol. 27, No. 10, 2011. pp. 1545-1557. doi:10.1002/cnm.1369
- G. Hadley and T. M. Whitin, “Analysis of Inventory Systems,” Prentice-Hall, New Jersey, 1963.
- F. S. Hillier and G. J. Lieberman, “Introduction to Operations Research,” McGraw Hill, New York, 2001.
- S. Nahmias, “Production & Operations Analysis,” McGraw-Hill, New York, 2009.
- Y. -S. P. Chiu and C. -K. Ting, “A Note on ‘Determining the Optimal Run Time for EPQ Model with Scrap, Rework and Stochastic Breakdowns’,” European Journal of Operational Research, Vol. 201, No. 2, 2010, pp. 641- 643. doi:10.1016/j.ejor.2009.03.014
- S. W. Chiu, “Robust Planning in Optimization for Production System Subject to Random Machine Breakdown and Failure in Rework,” Computers & Operations Research, Vol. 37, No. 5, 2010, pp. 899-908. doi:10.1016/j.cor.2009.03.016
- R. Mehdi, R. Nidhal and C. Anis, “Integrated Maintenance and Control Policy Based on Quality Control,” Computers and Industrial Engineering, Vol. 58, No. 3, 2010, pp. 443-451. doi:10.1016/j.cie.2009.11.002
- W.-N. Ma, D.-C. Gong and G. C. Lin, “An Optimal Common Production Cycle Time for Imperfect Production Processes with Scrap,” Mathematical and Computer Modeling, Vol. 52, No. 5-6, 2010, pp. 724-737. doi:10.1016/j.mcm.2010.04.024
- M. Henig and Y. Gerchak, “Structure of Periodic Review Policies in the Presence of Random Yield,” Operations Research, Vol. 38, 1990, pp. 634-643. doi:10.1287/opre.38.4.634
- C. H. Kim, Y. Hong and S. Y. Chang, “Optimal Production Run Length and Inspection Schedules in a Deteriorating Production Process,” IIE Transaction, Vol. 33, No. 5, 2001, pp. 421-426. doi:10.1080/07408170108936840
- M. J. Rosenblatt and H. L. Lee, “Economic Production Cycles with Imperfect Production Processes,” IIE Transaction, Vol. 18, No. 1, 1986, pp. 48-55. doi:10.1080/07408178608975329
- W. Shih, “Optimal Inventory Policies When Stock-Outs Result from Defective Products,” International Journal of Production Research, Vol. 18, No. 6, 1980, pp. 677-686. doi:10.1080/00207548008919699
- Y. -S. P. Chiu, F. -T. Cheng and H. -H. Chang, “Remarks on Optimization Process of Manufacturing System with Stochastic Breakdown and Rework,” Applied Mathematics Letters, Vol. 23, No. 10, 2010, pp. 1152-1155. doi:10.1016/j.aml.2010.03.023
- X. Zhang and Y. Gerchak, “Joint Lot Sizing and Inspection Policy in an EOQ Model with Random Yield,” IIE Transaction, Vol. 22, No. 1, 1990, pp. 41-47. doi:10.1080/07408179008964156
- R. E. Barlow and F. Proschan, “Mathematical Theory of Reliability,” John Wiley & Sons, New York, 1965.
- S. W. Chiu and Y. -S. P. Chiu, “Mathematical Modeling for Production System with Backlogging and Failure in Repair,” Journal of Scientific and Industrial Research, Vol. 65, 2006, pp. 499-506.
- S. W. Chiu, K. -K. Chen and J. -C. Yang, “Optimal Replenishment Policy for Manufacturing Systems with Failure in Rework, Backlogging and Random Breakdown,” Mathematical and Computer Modeling of Dynamical Systems, Vol. 15, No. 3, 2009, pp. 255-274. doi:10.1080/13873950902808602
- A. Grosfeld-Nir and Y. Gerchak, “Multistage Production to Order with Rework Capability,” Management Science, Vol. 48, 2002, pp. 652-664. doi:10.1287/mnsc.48.5.652.7802
- V. Makis, “Optimal Lot Sizing and Inspection Policy for an EMQ Model with Imperfect Inspections,” Naval Research Logistics, Vol. 45, No. 2, 1998, pp. 165-186. doi:10.1002/(SICI)1520-6750(199803)45:2<165::AID-NAV3>3.0.CO;2-6
- Y.-S. P. Chiu, K.-K. Chen and H.-H. Chang, “Solving an Economic Production Lot Size Problem with MultiDelivery Policy and Quality Assurance Using an Algebraic Approach,” Journal of Scientific & Industrial Research, Vol. 69, No. 12, 2010, pp. 926-929.
- B. J. Yum and E. D. McDowell, “Optimal Inspection Policies in a Serial Production System Including Scrap, Rework and Repair: An MILP Approach,” International Journal of Production Research, Vol. 25, 1987, pp. 1451- 1464.
- L. B. Schwarz, “A Simple Continuous Review Deterministic One-Warehouse N-Retailer Inventory Problem,” Management Science, Vol. 19, 1973, pp. 555-566. doi:10.1287/mnsc.19.5.555
- S. K. Goyal, “Integrated Inventory Model for a Single Supplier-Single Customer Problem,” International Journal of Production Research, Vol. 15, No. 1, 1977, pp. 107-111. doi:10.1080/00207547708943107
- B. Abdul-Jalbar, J. Gutiérrez and J. Sicilia, “Integer-Ratio Policies for Distribution/Inventory Systems,” International Journal of Production Research, Vol. 93, 2005, pp. 407-415.
- B. Bilgen, “Application of Fuzzy Mathematical Programming Approach to the Production Allocation and Distribution Supply Chain Network Problem,” Expert Systems with Applications, Vol. 37, No. 6, 2010, pp. 4488 -4495. doi:10.1016/j.eswa.2009.12.062
- U. Buscher and G. Lindner, “Optimizing a Production System with Rework and Equal Sized Batch Shipments,” Computers & Operations Research, Vol. 32, 2005, pp. 515-535.
- A. Diponegoro and B. R. Sarker, “Finite Horizon Planning for a Production System with Permitted Shortage and Fixed-Interval Deliveries,” Computers & Operations Research, Vol. 33, No. 8, 2006, pp. 2387-2404. doi:10.1016/j.cor.2005.02.019
- S. K. Goyal and F. Nebebe, “Determination of Economic Production-Shipment Policy for a Single-Vendor-SingleBuyer System,” European Journal of Operational Research, Vol. 121, No. 1, 2000, pp. 175-178. doi:10.1016/S0377-2217(99)00013-2
- R. M. Hill, “Optimizing a Production System with a Fixed Delivery Schedule,” Journal of Operational Research Society, Vol. 47, 1996, pp. 954-960.
- S. -L. Kim, A. Banerjee and J. Burton, “Production and Delivery Policies for Enhanced Supply Chain Partnerships,” International Journal of Production Research, Vol. 46, No. 22, 2008, pp. 6207-6229. doi:10.1080/00207540701472124
- D. Ojha, B. R. Sarker and P. Biswas, “An Optimal Batch Size for an Imperfect Production System with Quality Assurance and Rework,” International Journal of Production Research, Vol. 45, No. 14, 2007, pp. 3191-3214. doi:10.1080/00207540600711853
- B. R. Sarker and G. R. Parija, “An Optimal Batch Size for a Production System Operating under a Fixed-Quantity, Periodic Delivery Policy,” Journal of Operational Research Society, Vol. 45, 1994, pp. 891-900.
- R. A. Sarker and L. R. Khan, “An Optimal Batch Size under a Periodic Delivery Policy,” International Journal of Systems Science, Vol. 32, No. 9, 2001, pp. 1089-1099. doi:10.1080/00207720010015717
- L. B. Schwarz, B. L. Deuermeyer and R. D. Badinelli, “Fill-Rate Optimization in a One-Warehouse N-Identical Retailer Distribution System,” Management Science, Vol. 31, 1985, pp. 488-498. doi:10.1287/mnsc.31.4.488
- S. Viswanathan, “Optimal Strategy for the Integrated Vendor-Buyer Inventory Model,” European Journal of Operational Research, Vol. 105, No. 1, 1998, pp. 38-42. doi:10.1016/S0377-2217(97)00032-5
Appendix-A
Computation of Equation (11) is given below.
Recall Equation (10) as follows:
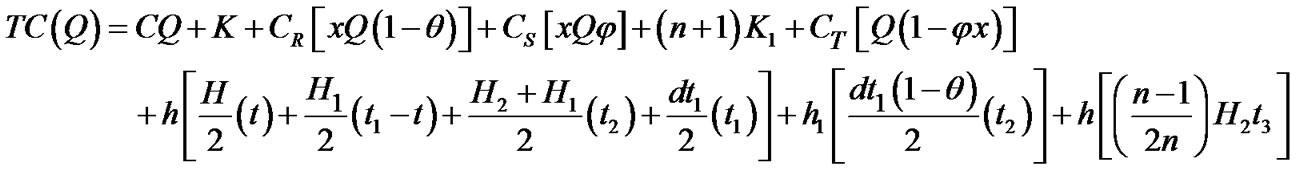 (10)
(10)
Substituting all related parameters from Equations (1) to (9) in Equation (10) one obtains
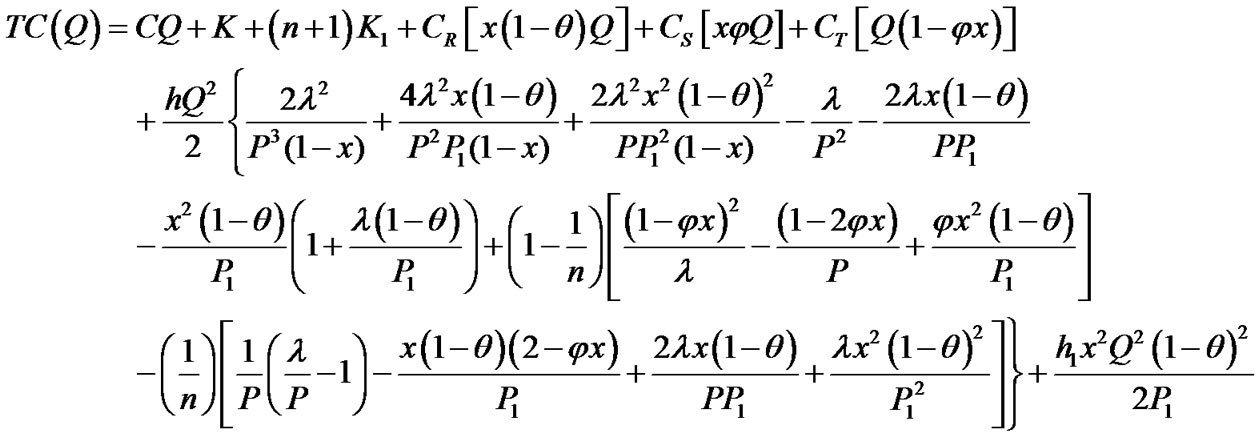 (A-1)
(A-1)
or
 (A-2)
(A-2)
Because
 (A-3)
(A-3)
and
 (A-4)
(A-4)
Substituting Equations (A-2) and (A-3) in Equation (A-4) one obtains
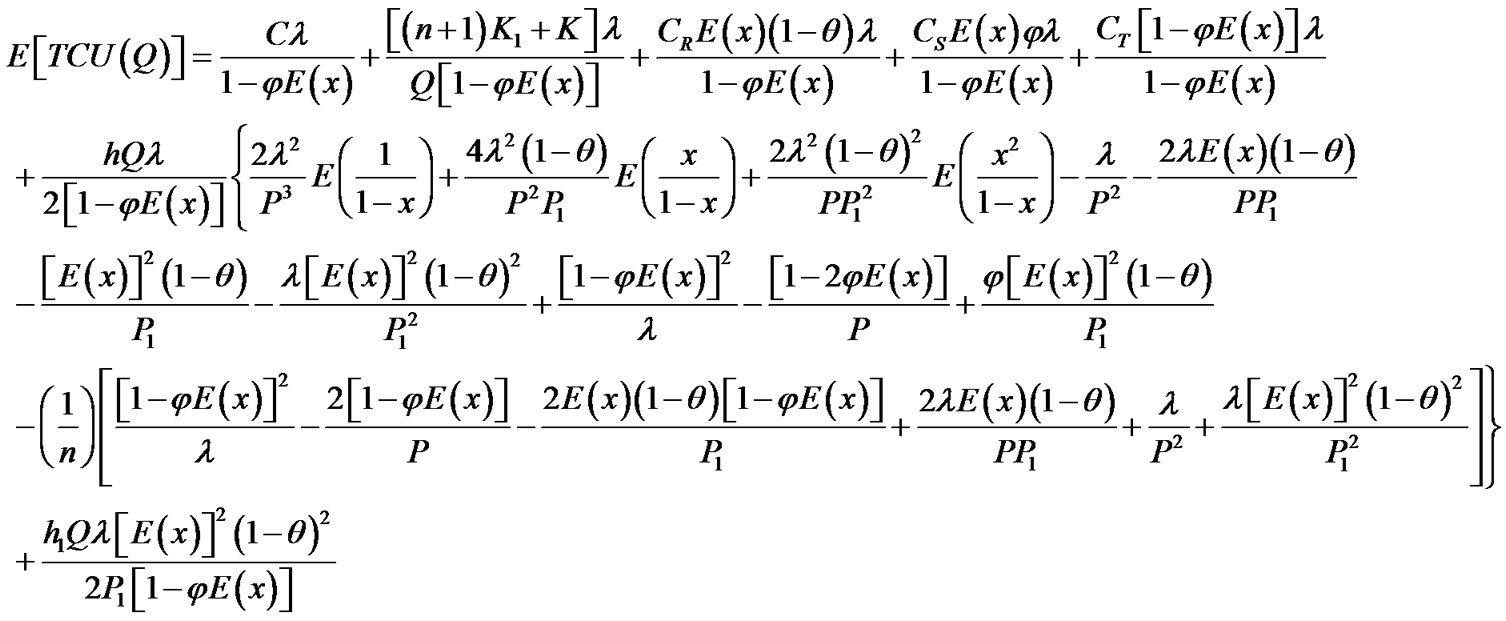 (A-5)
(A-5)
With further rearrangements one has
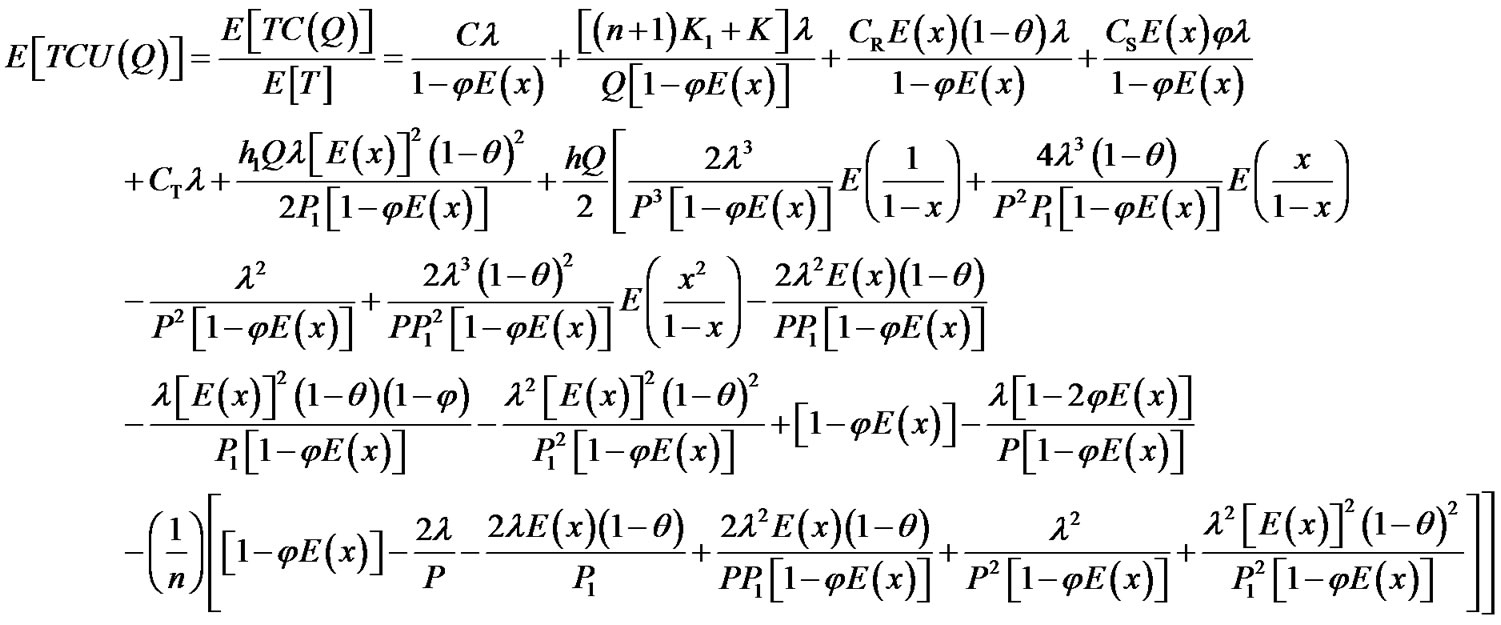 (11)
(11)

