ABSTRACT

Life Cycle Assessment (LCA) is a comprehensive method to evaluate all attributes or aspects of potential environmental impact throughout a product’s lifecycle. Financial impacts are often added to the systemic evaluation process to reflect both environmental and economic assessment. For the specific application of LCA informing design of new technologies, when numerous variables are undecided or under defined, the process of forming an inventory of complete dataset is very difficult. Accumulating the early data consumes time, and limits application of LCA to new technologies and projects. As such, LCA may not normally be associated with forecasting or guiding a design/production process with an incomplete data set. Here, a life cycle assessment optimization model (LCAO) is described for incomplete data sets, based on the life cycle inventory (LCI) hybrid method and a modified multiple criteria decision making (MCDM) approach. The approach requires data, but can proceed in the given an incomplete or uncertain data set. The model of the algorithm also shows promising results to reveal previously unknown key variables within the dataset, which can then facilitate the minimization of environmental impact while maximizing economic benefits in product design.

Keywords:Life Cycle Assessment, Optimization, Multiple Criteria Design

1. Introduction

Life Cycle Assessment (LCA) is a comprehensive method to evaluate all attributes or aspect of potential environmental impacts, human health and resources consumed throughout a product’s lifecycle. For example, a product undergoes stages of transformation from raw material, to material refinement and production, to material usage, and then to waste disposal or recycling (ISO, 2006). Often, financial impacts are added to the systemic evaluation process to integrate environmental and economic assessment [1] . One of the main potential applications of modern life cycle assessment (LCA) is to identify options for environmental and economic improvements in developing a new a technology or system. However, a challenge of LCA lies in identifying a compelling plan for moving forward with multiple, and often conflicting objectives from stakeholders, balancing environmental and economic drivers. Additionally, for a proposed technology or project, not yet in a stage of actual production, it is usually difficult to acquire a full inventory of specified data, and there still are many variables that should be decided. Therefore, LCA traditionally cannot be used to provide meaningful guidance for projects as a forecasting tool. This paper proposes a new LCA optimization model (LCAO), which can conduct in the condition of lack of sufficient data, help managers to determine variables to minimize environmental impact and maximize economic benefits, and finally find the “best” alternative with multiple and conflicting objectives.

In this paper we present a model based on the life cycle inventory (LCI) hybrid method, combining with a modified MCDM approach for this specific problem. There are five main features of the LCI + MCDM model: 1) Formulates the multi-objective problem based on a hybrid method; 2) Formulates a single objective problem for the entire system, from which the optimal solution can be solved according to the decision maker’s preference; 3) Can conduct both optimization process and LCA simultaneously; 4) Can be applied to new technologies in the condition of incomplete data set; 5) Maintains an iterative process to obtain more data, guided by the LCAO model.

The general framework of this model consists of 9 steps:

1.    Definition of Goals and Scope.

2.    Determination of independent variables in the system studied.

3.    Completion of LCI and numerical LCA with variables.

4.    Formulation of constraints for variables.

5.    Formulation of MCDM in term of LCA.

6.    Optimization and gaining the efficient set of solutions.

7.    Assigning weights for categories by paired comparison method.

8.    Scaling and formulation of single objective problem for the entire system.

9.    Iteration.

The first six steps will be discussed in Part 3, and the last three parts will be illustrated in Part 4.

2. Life Cycle Assessment

Measuring and reducing the environment impacts is necessary for sustainable development in human activities for providing goods and services, both of which could be summarized under the term “products”. Environment impact will be caused by the temporary use of land, by extracting resources, product manufacturing, waste and or material recycling, as well as waste disposal, all with the potential of releasing harmful substances into the environment. These emissions, interventions and consumptions lead to a wide range of environment impacts, such as climate change, acidification, stratospheric ozone depletion, eutrophication, tropospheric ozone creation, and depletion of resources, toxicological stress on human health and ecosystems, as well as noise.

A clear methodology exists to provide complimentary insights, besides current regulatory reactionary steps, to help measure and plan for reducing environmental impacts. Life Cycle Assessment (LCA) is a comprehensive method to evaluate all attributes or aspect of potential environmental impacts, human health and resources consumed throughout a product’s lifecycle, for example, from raw material obtaining, via production and use, to waste disposal (ISO, 2006). LCA defines product systems, such as technologies, via accounting models that describe physical systems in terms of their respective key elements (ISO, 2006).

The LCA process has matured considerably in the past several decades, but is still under development to reflect emerging sociological and ecological criteria under evaluation. The LCA methodological framework consists of four interconnected phases, depicted in Figure 1 (ISO, 2006):

1)    Goal and scope definition: describing the reason of study, determining the functional unit and selecting the system boundaries;

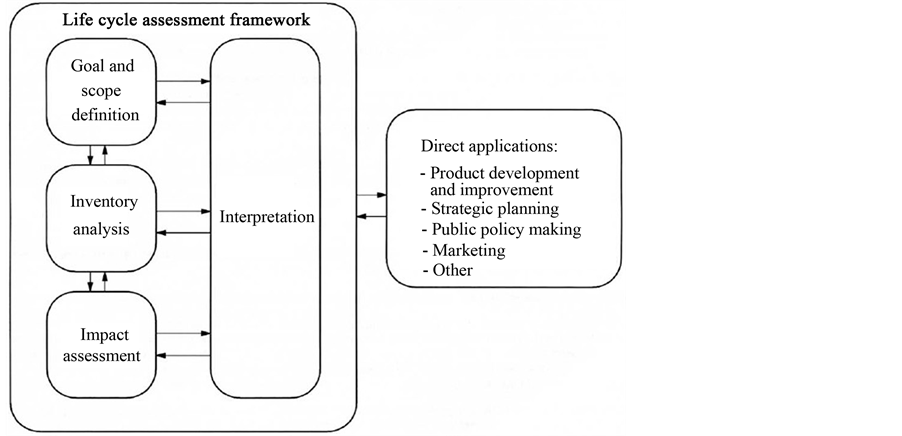
Figure 1. Life cycle assessment framework from ISO 14040: 2006. [4] .         

2)    Inventory analysis (LCI): quantifying relevant inputs and outputs of the system defined in the goal and scope definition phase, including data collection and calculation;

3)    Impact assessment (LCIA): aggregating the environmental burdens quantified in the Inventory Analysis into a limited set of recognized environmental impact categories, such as global warming, acidification, Ozone Depletion, etc.;

4)    Interpretation: using the results to reduce the environmental impacts associated with the product or process.

The life cycle inventory analysis phase is an inventory of input and output data in relation to the system being studied. It involves data collection and calculation procedures to quantify all the energy and material inputs, as well as outputs from the system, i.e. wastes and emissions. In addition to the detailed LCI, another traditional approach of LCI is industry/commodity level input/output (I/O) modeling [2] (e.g., Hall et al., 1992).

Another approach of LCI is Hybrid LCA. The general strategy is to minimize the use of input-output based data for major processes, by restricting its application only to the flows located at the margin of the system boundary, so that process specific data can be utilized as much as possible and the boundaries are expanded to the full system at the same time. In hybrid LCA, the I/O matrix A is converted to A', the environmental burden by industry matrix B in (1) should also be adjusted to an environmental intervention by commodity matrix, B' [3] . Therefore, the total environmental intervention due to an arbitrary final demand is then given by:

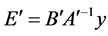(1)

The life cycle impact assessment phase (LCIA) provides further information to help evaluate LCI results from a product system, in order to get a better understanding of its environmental impacts, by providing factors for calculating and cross-comparing environmental intervention indicators of the potential environmental impacts in relation to the emissions, the wastes, and the resources consumed which are attributable to the provision of goods and services [4] .

Life Cycle Optimization and MCMD

To make LCA useful for projects in early develop, when data is sparse, a life cycle assessment and optimization model (LCAO) is proposed, which can conduct in the condition of lack of sufficient data, help managers to determine variables to minimize environmental impact and maximize economic benefits from the designing phase, and finally find the “best” alternative from multiple and conflicting objectives for the decision maker.

The main propose of Life Cycle optimization is to seek out a strong solution for the decision maker from within the efficient set of solutions. As already pointed out, it is impossible to improve an objective without losing others for a solution in the efficient set. Therefore, trade-offs between the objectives are inevitable to find the best compromise solution according to the goal and scope of the study LCAO also maintains the iterative of Life Cycle Assessment. As the process develops through time, more data will be obtained, and fewer variables need to be determined.

One possible methodology to identify the best solution in the context of multiple criteria is to assign weights to environmental and economic objectives indicating their significance, so that the problem is aggregated to a single objective optimization. In this paper, a modified method will be developed based on the rating method, the bordacount method, and the paired comparison method, to assign weights for each of the objective functions considered to then find the best solution to base a final decision within the designing phase.

3. Methods

3.1. Inventory Analysis

In this model, the total amount of industry output x required by an arbitrary final demand for industry output y is calculated by:

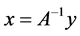(2)

where 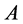is the Input-Output matrix, 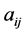represents the 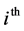industry’s output consumed to produce 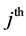industry’s output. Then, the environmental intervention (e.g., CO₂, SO₂, waste water, solid waste) for the society generated by an arbitrary final demand y can be calculated by:

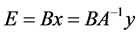(3)

E represents the total environmental intervention vector due to an arbitrary demand vector y. Matrix B gives environmental interventions for each dollar of output in each industry, and b_ij represents how much intervention 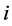produced by industry.

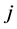3.2. Impact Assessment

According to ISO 14,040, there are three broad groups of environmental impact categories (resource use, human health consequences, and ecological consequences) that should be considered when defining the goal and scope of an LCA (Udo de Haes et al., 1999). Equation (4) provides an example of how indicator for each environmental impact category can be calculated from the LCI results utilizing generic characterization factors, which are the output of characterization models. These factors, in the form of databases, are available to practitioners in LCA support tools and literature.

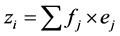(4)

where 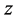denotes the category indicator (e.g., climate change, eutrophication, acidification or resource use, human health consequences and ecological consequences), f represents the characterization factor and e is the environmental intervention. Equation (4) can also rewrite as:

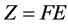(5)

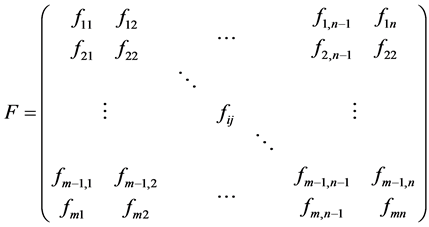(6)

where 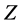denotes the category indicator vector, F represents the characterization factor matrix, 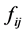means the amount of indicator 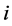caused by environmental intervention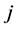. In hybrid LCA, Equation (5) is converted to

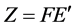(7)

3.3. Multiple Criteria in Life Cycle Assessment and Optimization Method (MCDM)

Because a number of distinct environmental impacts are considered in LCA, optimization problems associated with LCA are inevitably multiple criteria decision making problem (MCDM). Therefore, LCAO is formulated to optimize the system with multiple conflicting criteria (usually economic and environmental). The vector of environmental impact category indictors 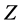can be calculated by Equation (5) or (7). The economic benefits could be represented by:

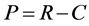(8)

where 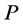is the present value of the system, R represents the revenue and C donates the cost.

Considering the sequence problem, the economic profits could be represents as:

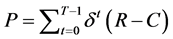(9)

where 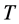is the total time periods considered, 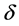is the discount rate.

A LCAO problem is looking to minimize the various environmental impacts while maximizing the economic benefits. It takes the following form:

(10)

Subject to:

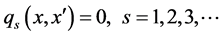
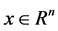
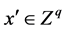
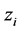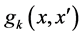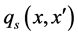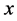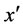where and are impact category indicator (e.g. resources use, human health consequences or ecological consequences) function and economic profit function., represent inequality (e.g., the capacity: the yield should less than a certain amount) and equality constraints (e.g., the production efficiency limited by technology: put 1 dollar’s coal will get 1.2 dollar’s electricity), and and denote the vectors of continuous and integer decision variables which could be the unknown data in the system we studied.

In a broader context, LCAO problem could be formulated as:

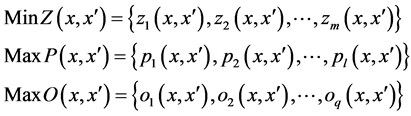(11)

Subject to:

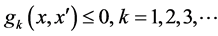
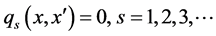
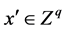
where the economic criteria vector P may contain short term profits and long term profits etc. the vector O represents other criteria to be considered (e.g., the energy efficiency and profitability per capita).The equality constraints include energy and material balances; the inequality constraints could represent material availabilities, emissions standards and production requirements, ranges of capacities etc. Continuous variables may be mass, energy and material flows, yield, pressures, compositions, sizes of units etc., while integer variables may be represented by the quantity of equipment, factories or transportation times, processing routes in the system.

If the discount rate is considered or nonlinear terms exist, (10) and (11) is a Mixed-Integer Nonlinear Programming (MINLP) problem. The MCDM problem (10) and (11) can be solved by spreadsheet analysis (Excel and Lin do have been used in this study), and the result is usually a set of efficient solutions instead of a “best” solution. By definition, the efficient solution means that an objective is able to be improved only at the loss of at least one other objective.

4. Results

In the previously discussed modified method, it is necessary to gain the bound (range) of each criterion from the efficient set of solutions first. These bounds can be calculated from (10) or (11) by spreadsheet. The next step is to conduct paired comparison and assign strength of preference with the reference of the bounds, using a ratio. For example, in the case that the range of the waste water is from 10 t to 1000 t and the range of economic profit is from $100,000 to $100,100, the question for decision makers could be that how many $100 you want to pay for reducing 990 t waste water. The final step of this modified paired comparison method is to determine the normalized criteria weights using n by n paired comparison matrix in Step 2.

For example, for criteria C₁, C₂, C₃, C₄, the paired comparison matrix can be obtained according to the bounds of them:

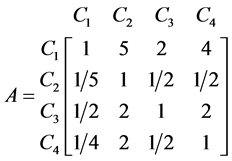(12)

where 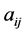means the weight of criteria 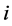divided by the weight of criteria.

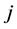Normalize matrix A:

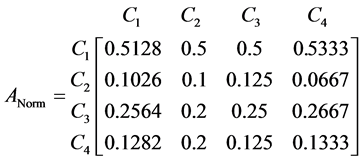(13)

Finally, weights can be calculated:

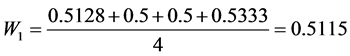
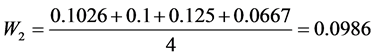
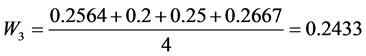
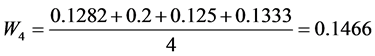
Single Objective Optimization

After assigning weights to environmental and economic objectives indicating their significance, the multiple criteria decision-making problem can be aggregated to a single objective optimization. However, it is important to note that scaling is necessary in this method, because the weights for environmental and economic objectives are all based on the bounds of criteria (objectives). In this study, linear normalization is used to keep consistent, since bounds are used as reference to gain weights. The criteria values are scaled as follows:

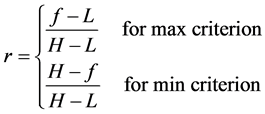(14)

where 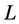represents the lowest bound of the criteria, 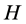means the highest bound of the criteria and f is the actual value function of the criteria. Here all the scaled criteria values will be between 0 and 1 and all the criteria are to maximize after scaling.

For (10), the final single objective function is:

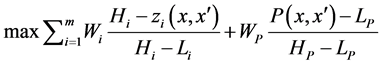(15)

s.t.

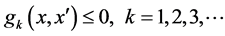
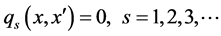
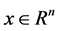
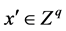
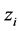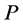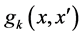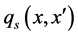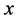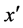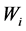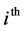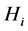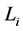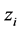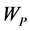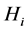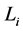where and are impact category indicators (environmental criteria) function and economic profit function., represent inequality and equality constraints, and and denote the vectors of continuous and integer decision variables. is the weight for the impact category indicators (environmental criteria), and are the highest and lowest bounds of, is the weight for the economic profit, and are the highest and lowest bounds of.

For the general Formula (11), the single objective function could be formulated as:

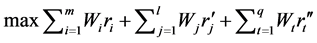(16)

s.t.

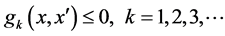
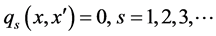
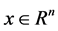
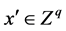
where 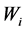is the weight for scaled impact category indicators (environmental criteria).

(17)

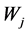is the weight for scaled economic profit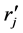

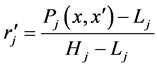(18)

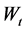is the weight for scaled other criteria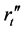

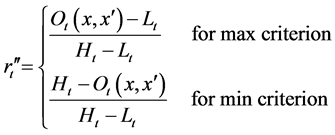(19)

The problem (15), (16) could be linear programming (LP) or nonlinear programming (NLP), depending on the relationship among variables. The approach for solving such problems is well developed in [5] [6] and several commercial software packages are also available online for the large scale LP or NLP problem, for example, XPRESS-MP [7] and [8] which are often applied in chemical engineering.

5. Conclusions

In addition to the function of evaluating environmental impacts and economic benefits of a process in a life cycle view to help decision-makers to choose the best project among alternatives, another function of improvement developed by LCAO is to provide guidance throughout the design and product process in the condition of data set that is incomplete. These guides include the target value of each variable to achieve the optimum performance and the relationship among variables for “what if” analysis. LCAO is an iterative process that eventually completes a data set.

In many cases, a number of possibilities for improvements exist and it is not always obvious which one of them results the optimum solution. There could also be more than one optimum solution. In this case a method of choosing the best solution from a set of optimal compromises is necessary. Therefore, combining LCAO with a modified multiple criteria decision-making (MCDM) approach helps decision-maker find the optimum solution set and the best compromised solution for every specific case. It should be noted that this combination may not be the best option in some cases, but it is another approach in MCDM to find the solution. The future work of LCAO will include testing the risk and variance as it applies to new technology, and performing sensitive analysis on variables.

References