World Journal of Cardiovascular Diseases
Vol.07 No.04(2017), Article ID:75929,12 pages
10.4236/wjcd.2017.74012
Estimation of Contraction Coefficient of Gorlin Equation for Assessment of Aortic Valve Area in Aortic Stenosis
Ricardo A. Migliore*, María E. Adaniya, Miguel Barranco, Guillermo Miramont, Silvia Gonzalez, Horacio Tamagusuku
Laboratory of Echocardiography, Department of Cardiology, Hospital Eva Perón, San Martín, Argentina

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 29, 2016; Accepted: April 27, 2017; Published: April 30, 2017
ABSTRACT
Background: The Gorlin equation is the reference method for the assessment of aortic valve area in aortic stenosis and is calculated using a constant, called the coefficient of contraction, which is empirically assumed to be 1. This coefficient is the ratio of effective aortic area to anatomic aortic area, and a value of 1 indicates that both are the same. The purpose of this study was to estimate the actual coefficient of contraction in patients with aortic stenosis and to evaluate its impact on aortic area as calculated by the Gorlin equation. Methods: We studied 17 patients with moderate to severe aortic stenosis. Effective aortic area was calculated using the continuity equation. Anatomic aortic area was obtained by planimetry with transesophageal echocardiography. Aortic valve area by the Gorlin equation was calculated from echocardiography data. The coefficient of contraction was derived as above. Results: The coefficient of contraction was inversely related to the pressure recovery. Effective area was correlated with anatomic area (r = 0.86, P < 0.01) but there was a high mean difference (0.22 ± 0.14 cm2). Aortic area by the Gorlin equation was not correlated with anatomic area, but the correlation became significant when the Gorlin equation was corrected for coefficient of contraction and pressure recovery. Conclusions: Using a coefficient of contraction of 1 in the Gorlin equation gives a poor correlation with anatomic area. Using the calculated coefficient of contraction for each patient and the mean gradient for pressure recovery improves the correlation with anatomic area. These facts could be taken in account when Gorlin equation is considered as the reference method.
Keywords:
Aortic Stenosis, Echocardiography, Hemodynamics Assessment

1. Introduction
The assessment of aortic stenosis severity depends in the clinical practice on the measurement of transvalvular gradients and aortic valve area [1] . In severe aortic stenosis, these gradients can be decreased, as a consequence of a low ejection fraction, or in patients with preserved ejection fraction, but a low stroke volume (paradoxical aortic stenosis), because the gradients depend on transvalvular flow [2] . For this reason, the severity of aortic stenosis is classified according to effective valve area (AVAe), calculated from the continuity equation, taking in account that there may be errors due to the incorrect measurement of the left ventricular outflow tract and its elliptical shape, or to factors affected by aortic root size, such as pressure recovery [3] [4] . Using this method, the area obtaining the AVAe, is the area of the vena contracta, which is located above the anatomic valve area (AVAa) close to the level of the sinotubular junction; this corresponds to the site of maximal jet velocity (registered by continuous-wave Doppler) that results from the momentum of the blood passing through the stenotic valve.
The method of the reference for the calculation of valve area is the Gorlin equation, which attempts to estimate the area from data obtained during catheterization, as follows: [5]

where Cc is the coefficient of contraction, Cd is the coefficient of discharge, 44.3 is the gravitational component ( ), and MG is the mean gradient. The Gorlin equation can be calculated from echocardiographic data with or without correction of MG for pressure recovery, because MG by Doppler is slightly greater than that by catheterization [4] [5] [6] . With regard to the constants used in the equation, in mitral stenosis Cc × Cd = 0.86, according to correlations obtained from surgery or autopsy, and in aortic stenosis, Cc × Cd = 1 has been established empirically [7] . Cd is the relationship between ideal gradient and real gradient, which cannot be measured in patients and is assumed to be 1. Cc is the ratio between the area of the vena contracta, or AVAe, and AVAa; in the case of aortic stenosis, a value of 1 assumes that both areas are equal, that is AVAe = AVAa. However, it has been demonstrated echocardiographically that AVAe is lower than AVAa because of the factors mentioned above (pressure recovery and the size of the aorta).
), and MG is the mean gradient. The Gorlin equation can be calculated from echocardiographic data with or without correction of MG for pressure recovery, because MG by Doppler is slightly greater than that by catheterization [4] [5] [6] . With regard to the constants used in the equation, in mitral stenosis Cc × Cd = 0.86, according to correlations obtained from surgery or autopsy, and in aortic stenosis, Cc × Cd = 1 has been established empirically [7] . Cd is the relationship between ideal gradient and real gradient, which cannot be measured in patients and is assumed to be 1. Cc is the ratio between the area of the vena contracta, or AVAe, and AVAa; in the case of aortic stenosis, a value of 1 assumes that both areas are equal, that is AVAe = AVAa. However, it has been demonstrated echocardiographically that AVAe is lower than AVAa because of the factors mentioned above (pressure recovery and the size of the aorta).
Taking into account that the value of Cc = 1 was established empirically, the objective of the present investigation was to estimate the Cc in aortic stenosis, based on the values of AVAa, obtained by transesophageal echocardiography (TEE), and AVAe, derived from the continuity equation, and to reassess its impact on the calculation of valve area using the Gorlin equation.
2. Methods
Twenty-three patients (age 65 ± 11 years, 13 male) who were referred for evaluation of valvular disease were studied prospectively. All had aortic stenosis of grade moderate to severe, as determined by transthoracic echocardiography and TEE. Patients with moderate or severe aortic or mitral regurgitation were excluded. The patients were questioned about cardiovascular risk factors and symptoms, and underwent a complete physical examination with blood pressure measurement prior to complete Doppler echocardiography. The protocol was approved by the Investigation Committee of our hospital.
2.1. Echocardiography
Examinations were performed with the patient in the left lateral decubitus position, using a TOSHIBA SSH140A ultrasound device with a 2.5 MHz transducer and ECG lead DII as reference.
End-diastolic and end-systolic diameters and ejection fraction were calculated according to the American Society of Echocardiography’s guidelines [8] . Left ventricular outflow tract (LVOT) diameter was measured from the long-axis parasternal view at the insertion point of the valve in mid-systole [9] and LVOT cross-sectional area was calculated as (LVOT diameter)2 × 0.785 [10] .
The aortic valve was examined using continuous-wave Doppler from the apical, right parasternal, suprasternal and subxiphoid views to obtain peak gradient, MG, and flow integral. LVOT flow was determined using pulsed-wave Doppler from the apical five-chamber view.
2.2. Transesophageal Echocardiography
TEE was performed under anesthesia with propofol [11] at an initial dose of 2 - 2.5 mg/kg (<60 years), 1.6 - 1.7 mg/kg (>60 years), or 0.7 mg/kg in aged patients followed by a maintenance dose with a bolus of 10 - 20 mg every 5 - 10 minutes until the end of the procedure. A multiplane Toshiba 5 MHz transducer was used and planimetry of the aortic valve was obtained from the short-axis view [12] . The view was considered adequate for planimetry if the aorta had a circular shape and all cusps were visualized simultaneously. AVA was defined as the orifice area between the cusps at the time of maximal opening in systole. An average of three consecutive measures was obtained.
2.3. Assessment of Aortic Stenosis
AVAe was calculated according to the continuity equation as:
AVAe = (LVOT area × integral flow of LVOT)/aortic integral flow.
AVAa was calculated from the TEE Doppler parameters using the Gorlin equation, as: [13]
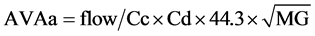
where aortic flow (mL/s) was calculated as stroke volume (LVOT area × LVOT integral flow) (mL) divided by left ventricular ejection time(s) measured from the beginning to the end of LVOT flow as recorded by pulsed-wave Doppler. Cc is the coefficient of contraction = AVAe/AVAa (TEE); Cd is the coefficient of discharge = 1; 44.3 is the gravitational component (44.3 = 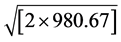 cm・s−2); and MG is the mean gradient obtained by continuous Doppler. MG net was calculated taking into account the pressure recovery according to the Baumgartner equation: [14] [15]
cm・s−2); and MG is the mean gradient obtained by continuous Doppler. MG net was calculated taking into account the pressure recovery according to the Baumgartner equation: [14] [15]

where VAo is the mean velocity through the aorta, VLVOT is the mean velocity in the LVOT, and Ao (cm2) is the area at the sinotubular junction.
2.4. Measurement Variability
To evaluate the intra- and inter-observer variability related to image analysis by transthoracic echocardiography and TEE; the measurement of AVAe and AVAa were repeated in 17 patients by two blinded observers with the use of the same set of images.
2.5. Statistical Analysis
Continuous variables were expressed as mean ± standard deviation. Pearson’s coefficient of correlation (r) and Bland-Altman analysis were used for correlations. A level of P < 0.05 was considered significant.
3. Results
Mean AVAe calculated by the continuity equation was 0.77 ± 0.2 cm2. Mean AVAa obtained by TEE was 0.98 ± 0.28 cm2, but in 5 patients (22%) it could not be determined; thus, 17 patients were included in the analysis. Clinical findings are shown in Table 1. Eight patients had a bicuspid aortic valve and 9 a tricuspid valve. Patients with a tricuspid valve were older than those with a bicuspid valve (70 ± 5.7 vs. 59 ± 8.3 years, P < 0.09), and had a larger AVAe (0.88 ± 0.18 vs. 0.61 ± 0.12 cm2, P < 0.03) and AVAa (1.13 ± 0.25 vs. 0.79 ± 0.14 cm2, P < 0.01)
Table 1. Clinical findings.
by TEE. PG, MG, and MG net were greater in patients with a bicuspid valve, but the difference was not significant. Ejection fraction, PG, MG, MG net, pressure recovery, and transvalvular flow are presented in Table 2.
There was a good correlation between AVAa by TEE and AVAe (r = 0.86, P < 0.01) (Figure 1(a)), but with a high mean difference (0.22 ± 0.14 cm2) (Table 2)
Table 2. Echocardiographic parameters.
*Mean gradient minus pressure recovery. AVAe: effective aortic valve area; AVAa: anatomic aortic valve area.
Figure 1. (a) Correlation between AVAa obtained by TEE and AVAe estimated by continuity equation. (b) Correlation between AVAa calculated by Gorlin equation and AVAa by TEE. (c) Correlation between AVAa using Cc calculated for each patient (AVAe/AVAa TEE) and AVAa by TEE. (d) Correlation between AVAa by Gorlin using Cc calculated for each patient and MG correctedfor pressure recoveryand AVA by TEE. AVAe: effective aortic valve area; AVAa: anatomic aortic valve area; TEE: transesophageal echocardiography; Cc: coefficient of contraction.
and with displacement of the regression line above the identity line, suggesting an overestimation of stenosis severity by AVAe calculated from the continuity equation. According to the regression equation (y = 1.1632x + 0.0878), an AVAe of 1 cm2 corresponded to an AVAa of 1.25 cm2.
There was no correlation between AVAa (TEE) and valve area calculated by the Gorlin equation when a Cc of 1 was used (r = 0.23, P:NS) (Figure 1(b)), but the correlation improved when the Cc calculated for each patient (AVAe/AVAa) was incorporated in the equation (r = 0.64, P < 0.01) (Figure 1(c)). The average Cc was 0.79 ± 0.13, with a range between 0.66 and 1 (only in 2 patients), and there was no difference between patients with a bicuspid and tricuspid aortic valve.
The correlation between AVAa (TEE) and the valve area by Gorlin equation was r = 0.71 (P < 0.01) when MG was corrected for pressure recovery (Figure 1(d)), with a low mean difference (0.09 ± 0.20 cm2), suggesting a good concordance between the two methods.
Cc had an inverse correlation with pressure recovery (Figure 2) (r = −0.61, P < 0.01), indicating that pressure recovery was greater for a greater difference between AVAe and AVAa (Table 3). The intra- and inter-observer variability of AVAe was 6% ± 5% and 8% ± 6% and for AVAa 5% ± 4% and 9% ± 5% respectively. Examples of AVAe, AVAa and the corresponding Cc in patients are shown in Figure 3.
Table 3. Coefficients of correlation and mean difference.
*P < 0.001. SD: standard deviation; AVAe: effective aortic valve area; AVAa: anatomic aortic valve area; TEE: transesophageal echocardiography; Cc: coefficient of contraction; PR: pressure recovery.
Figure 2. Correlation between pressure recovery and coefficient of contraction (Cc).
Figure 3. (a) Female patient, 68 years old, with dyspnea II (Top left) Recording of transvalvular aortic flow with continuous-wave Doppler simultaneously with phonocardiogram (PCG) and electrocardiogram (ECG). PG: peak gradient and MG: mean gradient. (Top right) Measurement of the left ventricular outflow tract (LVOT) diameter. (Bottom left) Recording of LVOT flow with pulsed-wave Doppler. (Bottom right) planimetry of AVAa in short-axis view by TEE. AVAa is greater than AVAe, with a Cc of 0.75. (b) Male patient, 78 years old, with heart failure functional class III (dyspnea). The order of the recordings is similar to figure A. Again, AVAa is greater than AVAe, with a Cc of 0.68. AVAe: effective aortic valve area; AVAa: anatomic aortic valve area; TEE: transesophageal echocardiography; Cc: coefficient of contraction.
4. Discussion
The reference method for the calculation of aortic valve area is the Gorlin equation, which was first reported in 1951 [10] . It was first used for the calculation of mitral valve area, and a coefficient of 0.7 was used based on the correlation with AVAa obtained from autopsy (6 patients) or surgical resection (5 patients). Because the duration of diastolic filling flow was measured from aortic closure (dicrotic notch) to the upstroke of aortic pressure (including isovolumic contraction and relaxation time), Cc was changed from 0.7 to 0.86 when simultaneous recording of the left atrium and ventricle became available [16] [17] . A Cc below 1 in mitral stenosis implies that effective valve area is less than anatomic valve area; however, in aortic stenosis Cc was established empirically as 1, indicating that AVAe is equal to AVAa. Several studies of the correlation between AVAe estimated by Doppler echocardiography and valve area estimated by cardiac catheterization, TEE, computed tomography and magnetic resonance demonstrated that AVAa is greater than AVAe, because AVAe is calculated using the maximal velocity at the vena contracta, a hydrodynamic area located above AVAa [12] [18] - [23] . Clavel et al. [24] studied with computed tomography and echocardiography patients with aortic stenosis and found a modest correlation (r = 0.57) between AVA planimetry (AVAa) by computed tomography and AVAe (echocardiography) with larger AVA planimetry compared with AVAe which are in concordance with our findings and other researchers [21] [25] . The guidelines of the European Society of Cardiology and the American Heart Association/American College of Cardiology make no distinction between echocardiographic or hemodynamic measurementsin the cutoff for the severity of aortic stenosis based on AVAe or AVAa and MG [26] [27] and they are assumed to be similar, though in daily practice MG is greater and AVA is lower by Doppler compared to the values obtained by catheterization.
In the present study, we found that AVAe was less than AVAa by TEE and the Cc calculated for each patient was variable (between 0.66 and 1), while the value of 1, as normally used in the Gorlin equation, was found only in 2 patients. For the same reason, AVAe was approximately 25% lower than AVAa by TEE, despite the good correlation between the two methods. The range of Cc found (0.66 - 1) is consistent with previous studies [28] [29] [30] . There were no significant differences in Cc in relation to the valve anatomy (bicuspid vs. tricuspid).
The correlation between AVAa by TEE and valve area by the Gorlin equation was not significant, because of the great dispersion of the values (Figure 1(b)), but it improved when it was corrected for the Cc of each patient and the pressure recovery. Regarding the last point, it is important to point out that pressure recovery depends on the size and elastic properties of the aorta; those parameters were not considered in the Gorlin equation and increase especially in smaller aortas (<30 mm) and in moderate to severe stenosis (AVAe 0.8 - 1.2 cm2) [31] [32] [33] . In addition, it should be kept in mind that Gorlin equation is derived from the Bernoulli equation, which describes a system with continuous flow and does not take in account the acceleration and inertia that apply in the case of pulsatile flow and contribute to an overestimation of the valve area. Furthermore, the equation ignores the conversion from mm H2O to mmHg and the density of the blood, in which the constant 44.3 should be replaced by 50 [18] . In addition, it has been demonstrated that, for a constant value of AVAa, AVAe may vary significantly, depending on whether the contraction is gradual or abrupt [34] . For the above reasons, the calculation of valve area using the Gorlin equation has limitations and is only an attempt to estimate AVAa. Furthermore, according to our findings, Cc is not constant, but varies from patient to patient. A better default value could be 0.8 instead of 1, given that AVAe is lower than AVAa in the majority of patients. However, when a constant value of 0.8 was used, the correlation did not improve (r = 0.26, P:NS).
Because of the limitations in the estimation of AVAa by the Gorlin equation, valve area should be determined using another imaging modality, such as TEE, three-dimensional echocardiography, magnetic resonance or computed tomography [34] [35] [36] [37] .
Limitations of the Study
The number of the patients studied was small. Planimetry of AVAa by TEE could not be accomplished in 22% of the patients due to impossibility of visualization of the entire orifice perimeter, in general associated with extensive calcification of the valve and acoustic shadow extending into aortic valve. Another limitation was the lack of correlation of AVAa with other techniques like computed tomography or magnetic resonance but there was not available. Determination of AVA by Gorlin equation with catheterization was not performed take in account the risk associated with the procedure [38] and the good correlation with Gorlin formula derived from echocardiography [39] .
5. Conclusion
The use of a constant of 1 for Cc in the Gorlin equation yielded a poor correlation with anatomic valve area. The correction of the values of Cc and MG for pressure recovery improved the correlation with AVAa by taking account of the fact that AVAa was greater than AVAe, elements that were not considered in the original Gorlin equation.
Author Contributions
Dr. Ricardo A. Migliore: concept, data analysis and interpretation.
Dr. Maria E. Adaniya: data acquisition, analysis and interpretation.
Dr. Miguel Barranco: data collection.
Dr. Guillermo Miramont: data collection.
Dr. Silvia Gonzalez: data collection.
Dr. Horacio Tamagusuku: critical revision of article.
Cite this paper
Migliore, R.A., Adaniya, M.E., Barranco, M., Miramont, G., Gonzalez, S. and Tamagusuku, H. (2017) Estimation of Contraction Coefficient of Gorlin Equation for Assessment of Aortic Valve Area in Aortic Stenosis. World Journal of Cardiovascular Diseases, 7, 119-130. https://doi.org/10.4236/wjcd.2017.74012
References
- 1. Carabello, B.A. (2002) Aortic Stenosis. The New England Journal of Medicine, 346, 677-682.
https://doi.org/10.1056/NEJMcp010846 - 2. Pibarot, P. and Dumesnil, J.G. (2012) Low-Flow, Low-Gradient Aortic Stenosis with Normal and Depressed Left Ventricular Ejection Fraction. Journal of the American College of Cardiology, 60, 1845-1853.
https://doi.org/10.1016/j.jacc.2012.06.051 - 3. Migliore, R.A. (2005) Structure and Function of the Left Ventricle. In: Piñeiro, D., Bustamante Labarta, M., Guevara, E., Migliore, R.A. and Roisinblit, J., Eds., Echocardiography, Panamericana, Buenos Aires.
- 4. Pibarot, P. and Dumesnil, J.G. (2007) New Concepts in Valvular Hemodynamics: Implications for Diagnosis and Treatment of Aortic Stenosis. Canadian Journal of Cardiology, 23, 40B-47B.
https://doi.org/10.1016/S0828-282X(07)71009-7 - 5. Dangas, G. and Gorlin, R. (1997) Changing Concepts in the Determination of Valvular Stenosis. Progress in Cardiovascular Diseases, 40, 55-64.
https://doi.org/10.1016/S0033-0620(97)80022-9 - 6. O’Sullivan, C.J., Praz, F., Stortecky, S., et al. (2014) Assessment of Low-Flow, Low-Gradient, Severe Aortic Stenosis: An Invasive Evaluation Is Required for Decision Making. EuroIntervention, 10, U61-U68.
https://doi.org/10.4244/eijv10sua9 - 7. Nishimura, R.A. and Carabello, B.A. (2012) Hemodynamics in the Cardiac Catheterization Laboratory of the 21st Century. Circulation, 125, 2138-2150.
https://doi.org/10.1161/CIRCULATIONAHA.111.060319 - 8. Lang, R.M., Badano, L.P., Mor-Avi, V., et al. (2015) Recommendations for Cardiac Chamber Quantification by Echocardiography in Adults: An Update from the American Society of Echocardiography and the European Association of Cardiovascular Imaging. Journal of the American Society of Echocardiography, 28, 1-39.e14.
https://doi.org/10.1016/j.echo.2014.10.003 - 9. Otto, C.M. (1997) Aortic Stenosis: Echocardiographic Evaluation of Disease Severity, Disease Progression, and the Role of Echocardiography in Clinical Decision Making. In: Otto, C.M., The Practice of Clinical Echocardiography, W.B. Saunders Company, Philadelphia, 405-432.
- 10. Oh, J.K., Seward, J.B. and Tajik, A.J. (1999) Hemodynamic Assessment. In: The Echo Manual, 2nd Edition, Lippincott-Raven, Philadelphia, 59-71.
- 11. Morgan, G.E., Mikhail, M.S. and Murray, M.J. (2005) Clinical Anesthesiology. 4th Edition, McGraw-Hill Medical.
- 12. Hoffmann, R., Flachskampf, F.A. and Hanrath, P. (1993) Planimetry of Orifice Area in Aortic Stenosis Using Multiplane Transesophageal Echocardiography. Journal of the American College of Cardiology, 22, 529-534.
- 13. Gorlin, R. and Gorlin, S.G. (1951) Hydraulic Formula for Calculation of the Area of the Stenotic Mitral Valve, Other Cardiac Valves, and Central Circulatory Shunts. I. American Heart Journal, 41, 1-29.
https://doi.org/10.1016/0002-8703(51)90002-6 - 14. Baumgartner, H., Steffenelli, T., Niederberger, J., et al. (1999) “Overestimation” of Catheter Gradients by Doppler Ultrasound in Patients with Aortic Stenosis: A Predictable Manifestation of Pressure Recovery. Journal of the American College of Cardiology, 33, 1655-1661.
- 15. Ragosta, M. (2008) Aortic Valve Disease. In: Ragosta, M., Ed., Textbook of Clinical Hemodynamics, Saunders, Philadelphia, 68-90.
- 16. Gorlin, W.B. and Gorlin, R. (1990) A Generalized Formulation of the Gorlin Formula for Calculating the Area of the Stenotic Mitral Valve and Other Stenotic Cardiac Valves. Journal of the American College of Cardiology, 15, 246-247.
- 17. Rosenhek, R. (2012) Aortic Stenosis: Disease Severity, Progression, Timing of Intervention and Role in Monitoring Transcatheter Valve Implantation. In: Otto, C.M., The Practice of Clinical Echocardiography, 4th Edition, Elsevier-Saunders Company, Philadelphia, 425-449.
- 18. Weyman, A.E., Scherrer-Crosbie, M. (2005) Aortic Stenosis: Physics and Physiology—What Do the Numbers Really Mean? Reviews in Cardiovascular Medicine, 6, 23-32.
- 19. Vahanian, A., Alfieri, O., Andreotti, F., et al. (2012) Guidelines on the Management of Valvular Heart Disease (Version 2012): The Joint Task Force on the Management of Valvular Heart Disease of the European Society of Cardiology (ESC) and the European Association for Cardio-Thoracic Surgery (EACTS). European Heart Journal, 33, 2451-2496.
https://doi.org/10.1093/eurheartj/ehs109 - 20. Bernard, Y., Meneveau, N., Vuillemenot, A., et al. (1997) Planimetry of Aortic Valve Area Using Multiplane Transesophageal Echocardiography Is Not a Reliable Method for Assessing Severity of Aortic Stenosis. Heart, 78, 68-73.
https://doi.org/10.1136/hrt.78.1.68 - 21. Ropers, D., Ropers, U., Marwan, M., et al. (2009) Comparison of Dual-Source Computed Tomography for the Quantification of the Aortic Valve Area in Patients with Aortic Stenosis versus Transthoracic Echocardiography and Invasive Hemodynamic Assessment. American Journal of Cardiology, 104, 1561-1567.
https://doi.org/10.1016/j.amjcard.2009.07.024 - 22. Malyar, N.M., Schlosser, T., Barkhausen, J., et al. (2008) Assessment of Aortic Valve Area in Aortic Stenosis Using Cardiac Magnetic Resonance Tomography: Comparison with Echocardiography. Cardiology, 109, 126-134.
- 23. House, C.M., Moriarty, K.A. and Nelson, W.B. (2014) Anatomic versus Effective Orifice Area in a Bicuspid Aortic Valve. Echocardiography, 31, 1023-1027.
https://doi.org/10.1111/echo.12619 - 24. Clavel, M.A., Malouf, J., Messika-Zeitoun, D., et al. (2015) Aortic Valve Area Calculation in Aortic Stenosis by CT and Doppler Echocardiography. JACC: Cardiovascular Imaging, 8, 248-257.
https://doi.org/10.1016/j.jcmg.2015.01.009 - 25. Larsen, L.H., Kofoed, K.F., Carstensen, H.G., et al. (2014) Aortic Valve Area Assessed with 320-Detector Computed Tomography: Comparison with Transthoracic Echocardiography. The International Journal of Cardiovascular Imaging, 30, 165-173.
https://doi.org/10.1007/s10554-013-0295-6 - 26. Nishimura, R.A., Otto, C.M., Bonow, R.O., et al. (2014) 2014 AHA/ACC Guideline for the Management of Patients with Valvular Heart Disease: A Report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. Circulation, 129, e521-e643.
https://doi.org/10.1161/cir.0000000000000031 - 27. Migliore, R.A., Adaniya, M.E., Barranco, M.A., et al. (2008) Effect of Effective Arterial Elastance on Left Ventricular Function in Severe Aortic Stenosis. Revista Argentina de Cardiología, 76, 278-285.
- 28. Garcia, D. and Kadem, L. (2006) What Do You Mean by Aortic Valve Area: Geometric Orifice Area, Effective Orifice Area, or Gorlin Area? The Journal of Heart Valve Disease, 15, 601-608.
- 29. Gilon, D., Cape, G.C., Handschumacher, M.D., et al. (2002) Effect of Three-Dimensional Echocardiographic Stereolithography and Patients Studies. Journal of the American College of Cardiology, 40, 1479-1486.
- 30. Flachskampf, F.A., Weyman, A.E., Guerrero, J.L., et al. (1990) Influence of Orifice Shape, Size, and Flow Rate on Effective Valve Area: An in Vitro Study. Journal of the American College of Cardiology, 15, 1173-1180.
- 31. Migliore, R.A., Adaniya, M.E., Mantilla, D., et al. (2010) Vascular and Valvular Load Low Flow, Low Gradient Severe Aortic Stenosis with Normal Ejection Fraction. Revista Argentina de Cardiología, 78, 30-38.
- 32. Laskey, W.K. and Kussmaul, W.G. (1994) Pressure Recovery in Aortic Valve Stenosis. Circulation, 89, 116-121.
https://doi.org/10.1161/01.CIR.89.1.116 - 33. Akins, C.W., Travis, B. and Yoganathan, A.P. (2008) Energy Loss for Evaluating Heart Valve Performance. The Journal of Thoracic and Cardiovascular Surgery, 136, 820-833.
https://doi.org/10.1016/j.jtcvs.2007.12.059 - 34. Clavel, M.A. and Pibarot, P. (2014) Assessment of Low-Flow, Low-Gradient Aortic Stenosis: Multimodality Imaging Is the Key to Success. EuroIntervention, 10, U52-U60.
https://doi.org/10.4244/eijv10sua8 - 35. Tandon, A. and Grayburn, P.A. (2013) Imaging of Low-Gradient Severe Aortic Stenosis. JACC: Cardiovascular Imaging, 6, 184-195.
https://doi.org/10.1016/j.jcmg.2012.11.005 - 36. Suradi, H., Byers, S., Green-Hess, D., et al. (2010) Feasibility of Using Real Time “Live 3D” Echocardiography to Visualize the Stenotic Aortic Valve. Echocardiography, 27, 1011-1020.
https://doi.org/10.1111/j.1540-8175.2010.01181.x - 37. Blot-Souletie, N., Hébrard, A., Acar, P., et al. (2007) Comparison of Accuracy of Aortic Valve Area Assessment in Aortic Stenosis by Real Time Three-Dimensional Echocardiography in Biplane Mode versus Two-Dimensional Transthoracic and Transesophageal Echocardiography. Echocardiography, 24, 1065-1072.
https://doi.org/10.1111/j.1540-8175.2007.00526.x - 38. Chambers, J., Bach, D., Dumesnil, J.G., et al. (2004) Crossing the Aortic Valve in Severe Aortic Stenosis: No Longer Acceptable? The Journal of Heart Valve Disease, 12, 344-346.
- 39. Teirstein, P., Yeager, M., Yock, P.G., et al. (1986) Doppler Echocardiographic Measurement of Aortic Valve Area in Aortic Stenosis: A Noninvasive Application of the Gorlin Formula. Journal of the American College of Cardiology, 8, 1059-1065.





