ABSTRACT

This paper provides innovative and effective instruments for the simplified analysis of serviceability limit states for pitched, kinked, and tapered GLT beams. Specifically, formulas for the evaluation of maximal horizontal and vertical displacements are derived from a recently-proposed Timoshenko-like non- prismatic beam model. Thereafter, the paper compares the proposed serviceability analysis formulas with other ones available in literature and with highly- refined 2D FE simulations in order to demonstrate the effectiveness of the proposed instruments. The proposed formulas lead to estimations that lie mainly on the conservative side and the errors are smaller than 10% (exceptionally up to 15%) in almost all of the cases of interest for practitioners. Conversely, the accuracy of the proposed formulas decreases for thick and highly-tapered beams since the beam model behind the proposed formulas cannot tackle local effects (like stress concentrations occurring at bearing and beam apex) that significantly influence the beam behavior for such geometries. Finally, the proposed formulas are more accurate than the ones available in literature since the latter ones often provide non-conservative estimations and errors greater than 20% (up to 120%).

Keywords:

Serviceability Analysis, Non-Prismatic Timber Beams, Tapered Beams, Pitched Beams, Maximal Displacements

1. Introduction

Nowadays, the usage of non-prismatic beams and pillars within GLT structures is a quite common practice in timber engineering since it allows for an efficient utilization of the material and, therefore, a more economical design. This trend benefits also from the technologies adopted in modern production plants that allow to easily obtain structural elements with complex geometries without significant increase of the production costs. Conversely, such optimized structural elements have to be designed carefully, otherwise the design optimization and the production effort are not paying off. In particular, in order to obtain an effective design, the modeling tools must accurately tackle two fundamental aspects: the mechanical properties of wood and the effects of beam geometry.

Regarding the mechanical properties of wood, its natural orthotropy causes the wooden elements to be extremely stiff and strong along the grain while the low stiffness and strength of wood perpendicularly to the fiber could represent a weak spot, maybe responsible for the premature failure of the structural element. Furthermore, the material orthotropy leads to significant shear deformations (also within slender elements) which, therefore, should always be considered within the design process [1] . Finally, looking at the design of wooden structures, the high ratio between the wood strength and stiffness leads the serviceability limit states to be often more restrictive than the ultimate limit states.

Concerning the effects of beam geometry, the variation of the cross-section size and shape causes the shear stress distributions within the cross-section to be substantially different from the prismatic beams [2] . Furthermore, the non- prismatic geometry induces significant stress orthogonal to the beam axis. Last but not least, both shear and orthogonal stresses could concentrate close to the cross-section boundaries. Such a problematic is known since the first half of the past century thanks to the analytic results discussed in [3] [4] , which provide the solution of equilibrium partial differential equations―i.e., the stress distribution―for an infinite long wedge loaded in the apex. Later on, Krahula [5] generalized the analytic results to linearly-tapered beams of arbitrary material whereas Riberholt [6] exploited the analytic results in order to predict stress distribution within tapered timber beams, proposing a former method for the simplified analysis of ultimate limit states of these particular beams. The effects of non- trivial stress distribution on beam failure were also extensively discussed in standard [1] [7] and advanced [8] literature and incorporated in most of national and international technical rules [9] [10] .

Unfortunately, the effects that the mentioned stress distribution has on displacements and stiffness of non-prismatic structural elements have not received a similar attention. In fact, also nowadays, the displacement analysis of non- prismatic beams are based on Euler-Bernoulli or Timoshenko beam ODEs in which cross-section area and inertia are tackled as parameters varying along the beam axis [7] [11] [12] [13] . Unfortunately, these modeling approaches are not able to tackle the complex stress distribution’s effects and lead to unsatisfactory results as noticed since the sixties of past century [14] [15] [16] .

The situation worsens considering FE modeling since non-prismatic beams are often approximated with a sequence of beam elements with piecewise-cons- tant thickness [17] [18] . Unfortunately, this approach introduces further approximation errors and even increases the computational efforts without any real benefit for the model accuracy [15] . As a consequence, several researchers suggest the usage of 2D or 3D FE in order to obtain accurate stiffness and displacement descriptions [19] . Unfortunately, the full FE discretization is not so common in timber engineering practice due to the approach complexity and the corresponding high computational cost (if compared with standard beam FE). Instead, simplified approaches dominate the design process despite their inconsistency and the coarse predictions contrast with the need of accurate serviceability analysis and the optimization goals [20] . As a consequence, the effective modeling of non-prismatic structural elements remains a research field opened to new contributions.

In recent years, several non-prismatic beam models have been proposed in an attempt to overcome the so far discussed problematic [21] [22] [23] [24] . Unfortunately, the most of them suffer from severe limitations e.g., they can tackle only symmetric and linearly tapered beams, present energy inconsistency, or lead to extremely complicated equations. In a recent work, Balduzzi et al. [25] proposed a simple Timoshenko-like model that overcomes the so far introduced problems. In particular, global equilibrium and compatibility ODEs can tackle also planar beams with complex geometry. Furthermore, the stress distribution within the cross-section satisfies boundary and internal equilibrium, recovering the analytic results discussed in [3] for simple geometry. Finally, the constitutive relations allow to catch the effects produced by non-trivial stress distribution and geometry on beam’s stiffness and displacements. Thereafter, the paper provides also analytic solution of the governing ODEs for simple geometries and several numerical examples, demonstrating that the model is effective and accurate. Later on, Balduzzi et al. [26] exploited the ODEs analytic solution for the evaluation of maximal displacements of several cambered GLT beams, indicating that the proposed beam model could be an effective tool for the serviceability analysis of non-prismatic GLT beams.

On the basis of such a work, this paper aims at i) detailing the derivation of formulas capable to estimate quantities of interest for practitioners during the serviceability limit state analysis; ii) validating the obtained results through the systematic comparison with other formulas existing in literature and with highly-refined numerical solutions for a large number of cases of practical interest, and iii) demonstrating that the proposed instruments significantly increase the accuracy of the serviceability states analysis.

The paper is structured as follows: Section 2 briefly resumes beam model’s ODEs; Section 3 derives the formulas for the evaluation of maximal displacements, introduces the other ones available in literature, and compares them from a theoretical point of view; Section 4 describes the validation campaign; Section 5 compares the results obtained with different methods and highly refined 2D FE analysis; and Section 6 resumes main advantages and weak spots of the proposed approach and delineates further research developments.

2. Timoshenko-Like Beam Model

This section recaps the Timoshenko-like beam model ODEs derived by Balduzzi et al. [25] and their analytic solution. Readers may refer to [25] for further details on the beam ODEs derivation and discussion.

The beam behaves under the hypothesis of small displacements and plane stress state and is made of a homogeneous and linear-elastic material. We introduce the beam length l, the beam longitudinal axis, 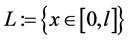, the beam center line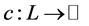, and the cross-section height (where 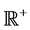in- dicates strictly positive real values).

The cross-section lower and upper boundaries, 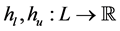are defined as follows

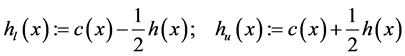(1)

and the 2D problem domain is defined as follows

(2)

Figure 1 represents the 2D domain, the adopted Cartesian coordinate system, the lower and upper boundaries and, the center line, and a generic cross-section.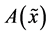

We assume that the lower and upper boundaries 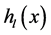and 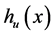are unloaded. Being 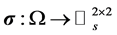the 2D symmetric stress tensor and the outward unit vector, the equilibrium on lower and upper boundaries reads. Using the unit vector definition

(3)

and the boundary equilibrium, we can express the shear stress as a function of the axial stress

(4)

where represents either or, depending on the point where we are evaluating the boundary equilibrium and the notation means the derivative with respect to the independent variable.

Finally, for convenience, we introduce the linear function defined as

(5)

2.1. Ordinary Differential Equations of Beam Model

The non-prismatic Timoshenko-like beam model uses the kinematics usually adopted for prismatic Timoshenko beam models (i.e., the cross-section is rigid in its plane and can rotate with respect to the center line). Therefore, the displacement field can be approximated as follows

(6)

where is the center-line horizontal displacement, is the cross-section rotation, and is the center-line vertical displacement.

The beam compatibility is expressed through the following ODEs

(7)

where the horizontal deformation, the curvature, and the shear deformation represent the generalized deformations.

We introduce the internal forces i.e., the horizontal internal force, the resulting bending moment, and the vertical internal force, respectively defined as follows

Being, , and the horizontal, bending, and vertical resulting loads, respectively, the beam equilibrium reads

(8)

Given the cross-section lower and upper boundary definitions (1) and the relations resulting from boundary equilibrium (4), the cross-section stress distributions can be expressed as

(9a)

(9b)

with

For the constitutive relations derivation, we consider the following simplified expression of stress potential

(10)

where and denote Young’s and shear modulus.

Substituting the stress recovery relations (9) into Equation (10), the beam constitutive relations can be obtained by

finally leading to the following expression of the beam constitutive relations

(11)

where

2.2. Analytical Solution of Beam Model ODEs

Substituting the constitutive relations (11) into the compatibility Equation (7) gives us the beam model ODEs in the following compact form

(12)

Since the matrix that collects equations’ coefficients has a lower triangular form with vanishing diagonal terms, the ODEs’ analytic solution can easily be obtained through an iterative procedure of row by row integration, starting from and arriving at. The resulting homogeneous solution of the beam model ODEs (12) is provided in Appendix A. Since the beam model is constituted by 6 first-order ODEs, the homogeneous solution depends on 6 parameters (, , , , , and, respectively) depending on the boundary conditions. With an analogous procedure, but considering a constant vertical load, it is possible to obtain the particular solution provided in Appendix B.

2.3. Highlights on Beam Model’s Capabilities and Limitations

It is worth noticing the following aspects deeply influencing the so far introduced beam model effectiveness.

・ The model equations (i.e., compatibility (7), equilibrium (8), and constitutive relations (11)), highlighted with a box in Section 2.1, provide a consistent description of internal forces, stresses, deformations, and displacements pro- perly accounting for the non-trivial geometry effects. Conversely, as already discussed in Section 1, the models available in literature are often incomplete or based on inconsistent assumptions. Therefore, they can provide only partial and not-satisfactory descriptions of the complex phenomena that occur within a non-prismatic beam. As an example, models that describe cross- section stress distribution [6] do not provide information about displacements whereas models that provide information on displacements [7] neglect the effects of cross-section stress distribution.

・ Referring to the simplified stress potential (10), the proposed model does not account for all the terms of the 2D stress potential, but only for the terms strictly related to axial and shear stresses. This choice allows for a significant reduction of the model complexity, but, conversely, it brings some limitations when this model is applied to beams with rapid variation of the cross- section or significant slope of the center line (i.e.,). Fortunately, the beams’ geometries that could be affected by significant errors are very rare in timber construction.

・ According to the adopted kinematics and stress representation, the introduced beam model has not the capability to tackle boundary effects. In particular, the proposed stress representation Equation (9) is valid only sufficiently far from initial and final cross-sections, corners (like the apex of a double pitched beam), and zones where concentrated loads are applied.

3. Formula for the Evaluation of Maximal Displacements

This section exploits the homogeneous and particular solutions derived in Section 2 to analytically evaluate the maximal displacements of GLT non-prismatic beams. Furthermore, the analytic results are compared with displacement solutions available from the literature to show the performance of the proposed model with respect to design’s state of art.

3.1. GLT Beam’s Geometry and Mechanical Properties Definitions

Considering the symmetric beam depicted in Figure 2, we introduce the following non-dimensional parameters

(13)

The additional geometrical parameters that characterize the beam geometry are defined as

(14)

Assuming and a pitched beam (see Figure 3(a)) is obtained, whereas assuming and, we obtain a generic tapered beam (see Figure 3(b)). Furthermore, setting and a kinked beam is obtained (see Figure 3(c)), whereas setting and

we obtain a double-pitched beam (see Figure 3(d)). Finally, assuming and the prismatic beam geometry is recovered.

The main parameters defining the mechanical response of wood are (i) the elastic modulus along the fiber direction, (ii) the elastic modulus perpendicular to the fiber direction, (iii) the Poisson’s coefficient, and (iv) the shear modulus. These properties are related to the Young’s modulus and shear modulus to be used within the beam constitutive relations (12) through the following expressions

(15a)

(15b)

where is the angle between the wood fiber direction and the horizontal axis, as depicted in Figure 2. The Young’s and shear moduli (15) are extrapolated from the rotated stiffness matrix defining the constitutive relations of the orthotropic material, assuming that ( [27] , Chapter 2).

3.2. Derivation of Simplified Formulas

In the following we evaluate the maximal displacements of non-prismatic GLT beam. In particular, we exploit the symmetry of the beam illustrated in Figure 2 in order to further simplify the problem. Therefore, we consider only the left half of the beam, imposing the following boundary conditions.

(16)

It is worth noticing that the boundary condition on horizontal displacements so far introduced disagrees with the constraints represented in Figure 2. Nevertheless, trivial calculations allow to recover the real displacement.

Asking the analytic solution reported in Appendices A and B to satisfy the boundary conditions (16), it is possible to determine the six coefficients for which are reported in Appendix C. Finally, the substitution of their values into the homogeneous solution leads to determine the analytic expressions of all the generalized quantities, , , , , and that we do not report for brevity.

3.3. Maximal Vertical Displacement

The maximal vertical displacement is one of the most significant parameters in serviceability states analysis. In the following, we compare the evaluation of such a quantity, done with the theory proposed in the present paper and with several other approaches available in literature.

3.3.1. Proposed Model

The maximal vertical displacement, occurring at the beam’s middle-span is expressed as the sum of a bending and a shear contribution

(17)

According to the model proposed in this paper, the bending and the shear coefficients, and are as follows

(18)

It is worth noticing that the bending coefficient does not depend on, while the shear coefficient depends on both coefficients and. Figure 4 shows the values of coefficients and evaluated for different and and it allows to recognize the effects of the beam rise on the total displacements. In particular, as expected for a prismatic beam (i.e., and), , confirming that the proposed beam model has the capability to recover the maximal displacements of a prismatic beam. Furthermore, for a kinked beam (see Figure 3(c)) with a rise equal to the height of the beam at the bearing (i.e., and), the shear contribution is 5 times bigger than the one obtained considering a prismatic beam. In other words, the beam rise deeply influences the beam behaviour and the proposed formula (17) has the capability to tackle this phenomena. Finally, the plot, corresponding to the double-pitched beam (see Figure 3(d)), represents the

minimum of all the possible plots. Therefore, we can conclude that the double- pitched beam represents the stiffer geometrical configuration for a non-prismatic beam.

3.3.2. Comparison with Results from the Literature

Schneider and Albert [28] propose the following formula for the evaluation of the maximal vertical displacement

(19)

where the coefficients and are defined as

(20)

These equations are used, among others, by Piazza et al. [1] and Angelis [29] .

Ozelton and Baird [7] propose an approach similar to (19), providing different formulas for the evaluation of the coefficients and. Nevertheless, the numerical values of the coefficients reported in [7] coincide with the ones coming from Equation (20) for all the values of of practical interest. Therefore, since the so far introduced approaches are equivalent, we do not report the formula provided by Ozelton and Baird [7] for brevity. Obviously, conclusions and remarks done for [28] are valid also for [7] .

A further formula for the evaluation of maximal displacement was proposed by Porteous and Kermani [13] , reading

(21)

where the coefficients and are defined as

(22)

It is worth having a closer look at the modeling approaches underlying the so far introduced formulas. As illustrated by Ozelton and Baird [7] , Equation (19) is based on a model that considers only the variation of cross-section area and inertia. As already noticed in Section 1, this approach is affected from heavy limitations that lead to coarse estimations. Furthermore, Equations (19) and (21) are derived considering a pitched beam (Figure 3(a)). Nonetheless, all the books and manuals cited within this section assume that the same coefficients can be considered valid for all the possible non-prismatic beam geometries depicted in Figure 3, neglecting the effects of the beam rise. Obviously, this assumption results to be inadequate looking at Figure 4. Finally, Equation (17) accounts for the real fiber orientation within the beam through and definition (15). On the contrary, Equations (19) and (21) use directly the mechanical properties of the material and, resulting therefore less rigorous.

Figure 5 shows a comparison between the coefficients (Equation (18)) evaluated for pitched and double-pitched beams, (Equation (20)), and (Equation (22)), respectively. It is worth highlighting that varies significantly considering a double-pitched beam (i.e.,) and a pitched beam (i.e.,). Specifically, for the double-pitched beam can easily be the half of the coefficient for the pitched beam, confirming that the parameter has a crucial role in determining the real beam displacements. Conversely, and are not influenced by variations of the beam rise since, as noticed before, they are derived from models unable to tackle this aspect. Finally, whereas the solution proposed by Schneider and Albert [28] is at least reasonably close to the one proposed in this paper for the double pitched beam, the model proposed by Porteous and Kermani [13] is substantially different for all the considered geometries. Further details about the comparison of these three models can be found in [25] .

3.4. Maximal Horizontal Displacement

The maximal horizontal displacement provides a fundamental information for the design of bearing devices. In the following, we compare the evaluation of such a quantity, done with the theory proposed in the present paper and with another approach available in literature.

3.4.1. Proposed Model

According to the kinematic assumptions (6), the maximal horizontal displacement can be expressed as

(23)

According to the model proposed in this paper, the maximal center-line horizontal displacement and the maximal rotation are estimated through Equations (24) and (26).

Maximal center-line horizontal displacement: In analogy with the maximal vertical displacement, we express the maximal horizontal displacement of the beam’s center-line as the sum of a bending and a shear contribution

(24)

Accordingly to the model proposed in this paper, the coefficients and are as follows

(25)

Figure 6 shows the values of coefficients and evaluated for different values of and and it allows to recognize the effects that beam taper and rise have on the maximal center-line horizontal displacement. In particular, for a double-pitched beam (i.e.,),. This means that, as expected, the vertical loads do not induce center-line horizontal displacements in consequence of the beam symmetries. Finally, as expected for a prismatic beam (i.e., and), , confirming once more that the proposed beam model has the capability to recover trivial solutions.

Maximal rotation: In analogy with the maximal vertical displacement, we express the maximal beam rotation as the sum of a bending and a shear contribution

(26)

According to the model proposed in this paper, the coefficients and are as follows

(27)

It is worth noticing that the bending coefficient does not depend on whereas the shear coefficient depends on both coefficients and.

Figure 7 shows the values of coefficients and evaluated for different values of and and it allows to recognize the effects of the beam taper and rise on the maximal cross-section rotation. In particular, as expected for a prismatic beam (i.e., and), and, confirming that, for this simple geometry, only bending contributes to the beam rotation. Furthermore, the bending contribution becomes negligible for large values of i.e.,. Finally, for, the plot― corresponding to the double-pitched beam (see Figure 3(d))―represents the minimum of all the possible plots. Therefore, Figure 7 confirms also that the double tapered beam represents the stiffer geometrical configuration for a non- prismatic beam.

3.4.2. Results from Literature

Piazza et al. [1] report the following formula in order to estimate the maximal horizontal displacement

(28)

Considering the boundary conditions (16) and assuming that the beam centerline is a rigid body, and are the horizontal displacement at the bearing and the vertical displacement at the middle-span length of a compatible rigid body motion. The latter contribution provides the exact value of the maximal horizontal displacement induced by the rotation only in case of prismatic beams. As a consequence, with increasing and (see Equation (13)), the result of Equation (28) is expected to become more and more inaccurate.

4. Numerical Validation

This section aims at determining the accuracy of the proposed formulas and comparing the performances of the proposed approach with the existing ones. Accordingly, it compares the results of the formulas introduced in Section 3 with the numerical results obtained through several FE analysis.

Some of the geometries considered within this section have no practical interest due to feasibility limits or convenience. Nevertheless, we decided to consider all of them in order to highlight all possible weaknesses of the models.

4.1. Case Definitions

The validation study consists of beams with different shapes, lengths, and upper boundary slopes. Accordingly, we classify each numerical test using the label Sllss structured as follows:

・ the first letter indicates the shape, where the letters, , and indicate pitched (Figure 3(a)), tapered (Figure 3(b)), and kinked (Figure 3(c)) beams, respectively.

・ the first two numbers indicate the beam length, where the numbers 05, 10, 20, and 30 indicate a total length of 5, 10, 20, and 30 m, respectively.

・ the latter two numbers indicate the slopes of the upper boundary expressed as a percentage, where the numbers 05, 10, 20, and 30 imply 5%, 10%, 20%, and 30% boundary slope, respectively.

Referring to Figure 2, in all the considered cases we assume that the initial beam height is equal to 1. For the tapered beams, we assume that the slope of the lower boundary is the half of the upper one i.e.,. For the kinked beams, we assume instead of in order to avoid numerical problems already highlighted by Balduzzi et al. [25] . Furthermore, it is also worth noticing that for this particular beam’s shape more effective modeling solutions (e.g., considering inclined prismatic beams) exist. Once more, we decided to consider also kinked beams in order to highlight all possible weaknesses of the models. Finally, we assume that wood’s fibers are parallel to the lower boundary i.e.,.

We assume that all the beams are made of wood classified as GL24h according to [30] . Therefore, we set E₀ = 9.667 Gpa, E₉₀ = 0.3250 Gpa, G = 0.6000 Gpa, and. The assumptions so far introduced are merely indicative. In fact, the usage of particular production technologies (like asymmetrically combined or cross laminated GLT) could modify significantly the material mechanical properties that therefore should be calibrated according to adequate experimental campaign [8] [31] . Finally, the distributed load is set to the artificial value of 200 kN/m.

Table 1, in Appendix D, details the geometrical and mechanical parameters for each case we are going to consider within the validation process. Table 1 allows to notice that the Young’s modulus could reduce more than 15% and the shear modulus could increase more than 5 times considering the real grain orientation, confirming that the effects of fiber orientation are not negligible.

4.2. 2D Numerical Solutions

For each beam geometry specified above, we compute the solution of the 2D elastic problem using the commercial FE package ABAQUS [32] . The following assumptions have been made.

・ Exploiting the problem symmetry, as done in the analytic model, we consider only the left half of the beam.

・ In order to model the bearing, we impede vertical displacements for the nodes that stay in the region and. This choice aims at avoiding singularity in 2D solution.

・ We constraint horizontal displacements for nodes at. Obviously, this choice leads to maximal horizontal displacements which are the half than the size of the real beam.

・ We neglect the dead weight of the beam.

・ Preliminary numerical simulations highlighted that the location of the linear distributed load within the 2D domain does not significantly influence the results. For this reason, we choose to apply the distributed load on the lower boundary. Furthermore, we set the magnitude of the applied load to be equal to such that the vertical reaction at the bearing will be equal to. The values of are given in Table 1.

・ The 2D domain of the beam is discretized with a structured mesh of linear triangles.

In order to validate the beam model we considered the following parameters.

・ The maximal horizontal displacement.

・ The maximal vertical displacement.

・ The maximal 2D horizontal displacement field.

・ The maximal 2D vertical displacement field.

In particular, we evaluate the maximal center-line horizontal displacement and the maximal rotation through the linear regression of the horizontal displacements of nodes at, whereas the maximal horizontal displacement is evaluated as

(29)

Finally, the maximal vertical displacement is evaluated as follows:

(30)

where the subscripts i and j refer to nodes at and, respectively.

It is worth recalling that the beam kinematics (6) assumes a rigid cross-section leading the beam model solution (Appendices A and B) to account only the mean values of cross-section displacements. Therefore, the beam model predicts a vanishing vertical displacement at in order to satisfy boundary conditions (16). Unlike that, the 2D FE model can catch cross-section deformations and stress concentrations that result in a non-vanishing mean-value of vertical displacements at and other local effects.

On the one hand, the usage of the maximal 2D displacements and is not appropriate for the validation of formulas (17) and (23) since they accounts for phenomena not tackled by the model introduced in Section 2.1. Aiming at overcome the inconsistency, we have introduced the parameters and (Equations (29) and (30)) that allow to eliminate most of the local effects from the FE solution and to provide reference solutions that could be used for a more rigorous beam model validation.

On the other hand, since the 2D FE simulations describe the physical problem more accurately than the beam model, the usage of and should reveal the effectiveness of the proposed formula in describing the real behavior of the beams under analysis. In particular, a large difference between and (and between and) indicates that local effects prevail on the beam behavior and therefore the beam model cannot be effective in predicting the displacement of that specific body. In order to highlight this aspect, we introduce the relative differences between the beam maximal displacements and the corresponding 2D maximal displacements

(31)

that provide a measure of the influence of local effects on the beam behavior. Obviously, the inconsistency between the beam model and the 2D solution is expected to vanish for slender beams, according to classical results in beam theories [33] .

In order to ensure the adoption of appropriate numerical results as a reference solution, we perform an accurate convergence analysis. Accordingly, for every specific beam length and shape we focus on the 30% boundary-slope geometry since it leads to the most distorted mesh. We consider a series of meshes starting with a characteristic element size of 0.1 m and successive refinements with a characteristic length of with increasing. We arrest the refinements when the relative difference between the maximal vertical displacement, evaluated with two subsequent meshes, is smaller than 10⁻⁴. Thereafter, the same characteristic element size is used for all the beams with the same shape and length. It is worth highlighting that the condition breaking the mesh refinements is highly restrictive and leads therefore to extremely refined meshes. A so big accuracy is usually not required in engineering practice, but is herein adopted in order to ensure that, reporting the reference solutions, any approximation error is smaller than the adopted number truncation.

Table 2 (in Appendix E) reports all the results of the ABAQUS simulations. The quantity el. size refers to the characteristic element size adopted in the simulation and # el. refers to the number of elements constituting the mesh. Table 2 reports also the values of and, defined in Equation (31).

5. Comparison and Discussion of Results

This section compares results obtained through the formulas introduced in Section 3 with the numerical results of the 2D FE analysis described in Section 4.2.

For each quantity, we consider the relative error

(32)

Differently from usual error definitions, in Equation (32) the absolute-value operators are omitted. This choice depends on the fact that we would highlight when formulas introduced in Section 3 overestimate (i.e., lead to a positive error) or underestimate (i.e., lead to a negative error) the numerical values which are considered as reference values. In authors’ opinion, this information is crucial since it allows to determine if the prediction is on the safe side or not.

Table 3 and Table 4 (in Appendix F) report the values of the estimated maximal displacements and their relative errors for all the considered cases. Figures 8-10 compare the relative errors obtained using formulas introduced in Section 3 for pitched, tapered, and kinked beams, respectively.

5.1. Pitched Beams

On the one hand, Figure 8(a) shows that the relative error of the proposed formula (17) is usually smaller than 2% and up to 10% for the 5 m long beams. On the other hand, Formula (19) proposed by Schneider and Albert [28] underestimates the maximal vertical displacements with relative errors often bigger than 10%. Finally, the formula (21) proposed by Porteous and Kermani [13] overestimates the maximal vertical displacements with errors that often exceed 100%. It is also worth recalling that the high values of (over 30%) indicate that 2D effects prevail for the 5 m long samples. Therefore, for this specific length, evaluations coming from all the considered beam models are not reliable due to intrinsic beam model limitations.

Figure 8(b) shows that the proposed formula (23) estimates the maximal horizontal displacement with an error usually smaller than 2.5% and up to 8.5% for the 5 m long beams. On the contrary, the formula (28) proposed by [1] estimates the maximal horizontal displacement with an error often bigger than 10% and up to 80% for the 5 m long beams. Once more, the high values of (over 40%) for the 5 m long samples indicate that evaluations coming from both the considered beam models are not reliable for these specific cases.

5.2. Tapered Beams

Figure 9(a) shows that the proposed model predictions exhibit a relative error generally smaller than 10%. The maximal error (33%) occurs in predicting the maximal vertical displacement of tapered beams width length l = 5 m where, nevertheless, the high value of (over 30%) indicates that the beam models are not effective. The formula (19) proposed by Schneider and Albert [28] underestimates the maximal vertical displacement with a relative error up to 20% even for the long beams. Finally, the formula (21) proposed by Porteous and Kermani [13] leads to very inaccurate predictions, with a error that exceeds 80%.

Figure 9(b) shows that the errors on the prediction of the maximal horizontal displacement (see Equation (23)) are smaller than 10% and up to 33% for the 5 m long beam. Conversely, the errors relative to the formula (28) proposed by Piazza et al. [1] tends to underestimate the maximal horizontal displacement up to 20% also for slender beams.

5.3. Kinked Beams

Figure 10(a) shows that the proposed formula (17) predicts the maximal vertical displacement of kinked beams with a relative error exceptionally bigger than 10%. As usual, more significant errors occur for the 5 m long beams for which the high value of indicates that 2D effects prevail and therefore the beam model is no longer effective. Both the formulas (19) and (21) underestimate the maximal vertical displacements and leads to similar relative errors that often overcome 20%. It is worth recalling that, as discussed in Section 3.3.2, both Equations (19) and (21) neglect the beam rise’s effects and therefore the provided estimation coincides with the maximal vertical displacement of a prismatic beam with thickness and length.

Figure 10(b) shows that the proposed approach (23) leads to relative errors exceptionally bigger than 10% and up to 40% only for the beams of length l = 5 m. Moreover, the formula (28) proposed by Piazza et al. [1] usually underestimates the maximal horizontal displacement, leading to errors that often overcome 20%.

6. Conclusions

This paper derives several formulas for the simplified analysis of serviceability limit states from a recently proposed Timoshenko-like model for a non-prismatic beam. The main advantage of the Timoshenko-like model is its capability to consistently tackle the effects of geometry on stress distributions, constitutive relations, equilibrium, and compatibility equations. Therefore, the resulting for- mulas provide an accurate prediction of the maximal displacements.

The comparison of the proposed formulas with highly refined 2D FE solutions allows the following conclusions.

・ The errors obtained using the proposed formulas are smaller than 10% in most cases.

・ Only when the proposed formulas are applied to thick beams (), they could induce more heavy errors, exceptionally over 30%. Nonetheless, numerical results reveal also that 2D effects certainly prevail for thick beams, leading any evaluation coming from all the considered beam models not reliable.

・ The proposed formulas provide estimates which lie mainly on the conservative side of safety.

The comparison with commonly used approaches allows to conclude that the proposed formulas are significantly more accurate. In particular, the literature review and the numerical results highlight the following weak spots of the approaches proposed in literature.

・ The majority of formulas available in literature are derived from models that often contradict each other e.g., neglecting the effects of beam rise (see Equations (19) and (21)), not considering the effects of stress distribution (see Equation (21)), or not accounting the real beam rotation (see Equation (28)). Therefore they can provide only partial descriptions of the complex phenomena that occur within a non-prismatic beam.

・ The maximal vertical displacement estimate proposed by Schneider and Albert [28] is more accurate than the one proposed by Porteous and Kermani [13] . However, it provides non-conservative estimations with relative errors often larger than 20% also for slender beams.

・ The maximal vertical displacement estimate proposed by Porteous and Kermani [13] leads to errors over 100% also for slender beams.

・ The formula proposed by Piazza et al. [1] is less reliable than the one proposed in this paper, since it provides non-conservative estimations with relative errors that are often bigger than 20% also for slender beams.

Therefore, the proposed approach represents a significant enhancement of the instruments that practitioners can use for the design of GLT beams since the proposed formulas, derived from a highly consistent model, result to be more accurate than the existing ones for most of the cases of interest for practitioners.

Further developments will include the consideration of other load conditions, beam geometries (like cambered beams), and the derivation of more refined instruments (e.g., analytic models and FE), capable to take into account the entire stress potential, generic boundary conditions, and more complicated geometries like asymmetric or curved beams.

Acknowledgements

This work was funded by the Cariplo Foundation through the Project # 2013- 1779 “iCardioCloud”, the Foundation Banca del Monte di Lombardia― Progetto Professionalitá Ivano Benchi through the Project # 1056 “Enhancing Competences in Wooden Structure Design”, and the Austrian Science Found (FWF) trough the Project # M 2009-N32 “e²-WoodS Enhancing Engineering Analysis of Wooden Structures”. Finally, authors would like to acknowledge Prof. Maurizio Piazza for the kind answer and collaboration.

Cite this paper

Balduzzi, G., Hochreiner, G., Füssl, J. and Auricchio, F. (2017) Serviceability Analysis of Non-Prismatic Timber Beams: Derivation and Validation of New and Effective Straightforward Formulas. Open Journal of Civil Engineering, 7, 32-62. https://doi.org/10.4236/ojce.2017.71003

References

Appendix

A. Homogeneous Solution

In the following we report the homogeneous solution of Equations (7), (8), and (11). It assumes that and.

B. Particular Solution

In the following we report the particular solution of Equations (7), (8), and (11), evaluated assuming a homogeneous vertical load. It assumes that and.

C. Evaluation of the Homogeneous-Solution Coefficients

In the following we report the values of homogeneous-solution coefficients obtained imposing the boundary condition (16).

D. Case’s Geometry

In the following we report the values of parameters that define the geometry of each case.

E. ABAQUS Results

In the following we report the values of ABAQUS results used as reference solutions for the numerical validation of the proposed formulas.

F. Displacement Estimations and Relative Errors

In the following we report the estimations of maximal displacements evaluated with different formulas and their relative errors.