Open Journal of Civil Engineering
Vol.06 No.01(2016), Article ID:64131,12 pages
10.4236/ojce.2016.61003
Nonlinear FEA of Pile Group Subjected to Lateral Load
V. A. Sawant, K. B. Ladhane
Department of Civil Engineering, Indian Institute of Technology Roorkee, Roorkee, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 February 2016; accepted 26 February 2016; published 29 February 2016
ABSTRACT
A finite element method based program has been developed to perform the static nonlinear analysis of pile group with six different configurations subjected to lateral loads. The pile has been assumed to remain elastic all the time whereas the soil has been assumed to undergo plastic yielding following von Mises yield criterion. The formulation of elasto-plastic analysis following von Mises yield criterion has been explained. The effect of Drucker-Prager and Mohr Coulomb yield criteria on the response of pile group is also investigated. The whole analysis is based on incremental load application. The external load is applied in small increments and the stresses are initially computed assuming elastic constitutive relation. Significant effect of soil nonlinearity is observed at smaller pile spacing which reduces with increase in spacing.
Keywords:
Pile, Lateral Load, Constitutive Matrix, Stress Invariants, Yield Criterion

1. Introduction
Nonlinear p-y analysis is the most widely used method for design of laterally loaded piles due to its simplicity; the successful application of a p-y method depends upon the availability of detailed information on a spatial distribution of soil properties which are key factors in the design of laterally loaded deep foundation. The subgrade reaction method models soils as Winkler springs and piles as beams; hence, pile geometry can be considered only indirectly. The finite element method provides a more precise tool that is capable of modelling soil continuity, soil nonlinearity, pile-soil interface behaviour, and 3-D boundary conditions. It is more rigorous in its analytical methodology than any other existing methods. Randolph [1] used linear strain triangles in the semi- analytical finite element formulation to avoid special integration techniques. From the results of parametric study, a simplified expression was developed for the response of single and group piles embedded in elastic soil. The nonlinear behaviour of pile group was studied using 3-D FEA with nonlinear elastic soil model [2] [3] . In order to include the interaction effects involving relative slip and separation, a thin layer of interface element was used. Najjar and Zaman [4] [5] studied the effects of loading sequence and soil nonlinearity on the deformation behaviour of a pile group using a nonlinear 3-D finite element technique. Ladhane and Sawant [6] presented dynamic analysis of pile group and examined the effect of different pile configurations on dynamic response.
The review of literature has revealed that behaviour of laterally loaded piles is significantly influenced by the material non-linearity. Behaviour of pile group is further influenced by the arrangements of piles in the group. A 3-D finite element program has been developed for the analysis of a pile groups in clay considering the above aspects. Soil and pile media have been discretised into 3-D isoparametric continuum elements. The pile elements have been assumed to remain in elastic state at all the time. On the other hand, the soil elements are assumed to undergo plastic yielding according to the von Mises yield criterion. This model has been selected because it is suitable for analyzing the behaviour of purely cohesive soils under undrained condition. To simulate the stress transfer between soil and pile under lateral load, interface elements have been introduced at the soil-pile interface. Normal and tangential stiffness of these elements are assumed in such a way that shearing at the soil pile interface is allowed but gapping will be restricted. The formulation and implementation of additional features required for incorporating nonlinear behaviour are presented in this paper.
2. Constitutive Model
Mainly, there are two types of materials involved in present study i.e. reinforced concrete and soil. The pile material is treated as linear elastic, whereas, the soil is replaced by an idealised material which behaves elastically up to some state of stress at which yielding occurs and beyond yielding, the theory of plasticity is implemented to account for the constitutive law of the soil. The constitutive relationships arising from the theory of plasticity are incremental in nature due to the stress path dependence of the material behaviour. The essential features of the plasticity theory are [7] :
・ A yield function, separates the elastic and plastic states of stresses in the body under consideration.
・ A plastic potential function defining the direction of plastic straining when yielding occurs (flow rule).
・ A hardening/softening law describing the dependence of the yield function on the plastic strains.
In the present study, von-Mises, Drucker-Prager [8] and modified Mohr-Coulomb [9] models have been considered. Viladkar et al. [7] have converted these models into convenient forms to make the computational aspect simple and presented a generalized approach to elasto-plastic finite element analysis. The associative flow rule is assumed, in which the yield function and plastic potential function are expressed by same function. The Yield criterions used to identify the onset of the yielding in the soil are explained here. Most of them are defined in terms of stress invariants. Here J1, J2, J3 are first, second and third stress invariant and 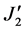 is second stress invariant of the deviatoric stress components.
is second stress invariant of the deviatoric stress components.
2.1. von-Mises Yield Criterion
Figure 1 shows the Graphical representation of von Mises yield criteria in deviatoric plane. When plotted in principal stress space it appears as circular cylinder whose central axis coincides with space diagonal. von-Mises yield function is approximation to the Tresca yield function and expressed in terms of 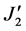 and material constant K as,
and material constant K as,
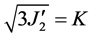 (1)
(1)
2.2. Drucker-Prager Yield Criterion
An approximation to the Mohr-Coulomb law was presented by Drucker and Prager as a modification of the von- Mises yield criterion. The influence of the hydrostatic stress component on yielding was introduced by inclusion of an additional term in the von-Mises expression as:
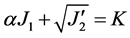 (2)
(2)
where, a and K are material constants, which may be related to Coulomb’s material constants c and j. Figure 1 shows graphical representation of Drucker-Prager and Mohr-Coulumb yield criteria in deviatoric plane. In order
Figure 1. Representation of yield criteria in deviatoric plane.
to make the Drucker-Prager circle coincide with the inner (Equation (3a)) and outer (Equation (3b)) apices of the Mohr-Coulomb hexagon at any section, it can be shown that [7] :
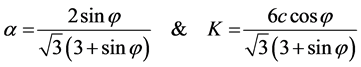 (3a)
(3a)
 (3b)
(3b)
However, since the values of c and j are determined by using conventional triaxial compression tests, these are different from those determined under a plane strain condition. Under this plane strain condition, the values of a and K can be expressed as:
 (3c)
(3c)
The two material parameters a and K for the Drucker-Prager model can be determined from the slope and intercept of the failure envelope plotted in the J1-( )1/2 space.
)1/2 space.
2.3. Mohr-Coulomb Yield Criterion
This criteria possess angular vertices at which the gradient with respect to the stresses, and hence the elasto- plastic constitutive law, is undefined at q = ±30˚ (Figure 1). A satisfactory method for dealing with these singularities is needed as they are often encountered in finite element computations. One technique for dealing with this problem has been discussed by Owen and Hinton [10] . In the vicinity of the vertices, their procedure uses the Drucker-Prager criterion to round-off the Mohr-Coulomb criterion. Another modified yield function suggested by Sloan and Brooker [9] is used to round-off these vertices. When used in conjunction with the parent yield function, the modified yield function results in a yield surface which is continuous and differentiable for all values of the stresses. The modified yield function is used in the vicinity of the vertices. The Mohr-Coulomb yield criterion is defined by following expression,
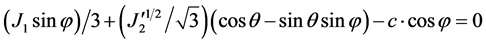 (4)
(4)
In which,
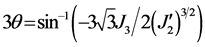 (−30˚ ≤ θ ≤ 30˚)
(−30˚ ≤ θ ≤ 30˚)
To avoid the singularities at the vertices of the Mohr-Coulomb surface, Sloan and Brooker [9] assume a different type of yield surface whenever q approaches ±30˚. In practice, the modified yield criterion is used whenever,
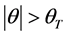
where, qT is specified and represents the absolute value of the angle at which the transition occurs. To ensure that the Mohr-Coulomb yield surface is modelled with acceptable accuracy, qT should typically be in the range 25˚ to 29˚. At these transition points modified function is used which is expressed as,
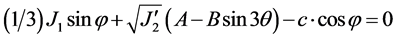 (5)
(5)
where,
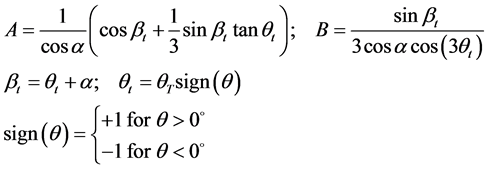
2.4. Elasto-Plastic Constitutive Matrix
Relation between incremental stresses, {Dσ} and incremental strains {De} in elasto-plastic state is given as,
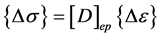 (6)
(6)
where, [D]ep elasto-plastic constitutive matrix.

[D]ep represents the elasto-plastic constitutive matrix. Parameter A depends on type of plasticity (e.g. perfect plasticity, strain hardening/softening plasticity or work hardening/softening plasticity). For perfectly plastic material, A = 0 and k = constant.
In the present study, associated (yield and potential surface coincides) flow rule is considered which gives symmetric constitutive matrix and consequently symmetric global stiffness matrix. This helps in reducing memory requirement for storage as well as time of computation.
3. Elasto-Plastic Constitutive Matrix
Nayak and Zienkiewicz [11] have converted the yield criteria into convenient forms to make the computational aspect simple and presented a generalized approach to elasto-plastic finite element analysis. Further, Viladkar et al. [7] transform several yield criteria with isotropic hardening and associated flow characteristics into convenient forms and make them available for easy implementation into the finite element codes.
This formulation is due to Nayak and Zienkiewicz [11] and Viladkar et al. [7] and is achieved by expressing the yield function as,

where, q is an alternative to the third stress invariant and determined by,

Here J1, J2, J3 are first, second and third stress invariant and 
The flow vector, a, is rewritten in terms of J1, 

Substituting 

where,
Calculation of C1, C2 and C3:
Differentiating Equation (9) with respect to s,
Substituting in Equation (18),

Simplifying radical in third term from above equation,

Substituting in Equation (12),

From Equations (11) and (14)

Calculation of a1, a2 and a3:
Following are the stress invariants required to evaluate the constants a1, a2 and a3.
The stress invariants are given as,

The second deviatoric stress invariants is given as,
From Equations (11) and (16) and substituting



The constants C1, C2 and C3 can be evaluated from the expression of yield function using Equation (15).
Nonlinear Solution Algorithm
The total load is applied in the ten equal increments and the stiffness matrix, [K] is kept constant for all the load increments in Figure 2. Following is the algorithm used for nonlinear analysis:
1) Apply incremental load 

2) Update the total displacements ui for ith increment by adding incremental displacement 

3) Set me = 0, where me indicates number of yielded elements.
4) For each element, set mp = 0 (number of yielded points within the given element), obtain the element incremental displacement vector 

5) For each Gauss point, compute the incremental stress 


Check for yield, if the point have not yielded then go to next Gauss point, else, set mp = mp + 1, and calculate extra stress over yield stress, {Δσ}ext

Set total stress at yield level

Update the additional force vector to be applied in next iteration

Complete loop over the Gauss points of the element
6) If mp > 0, then assemble load vector 
7) Repeat Step 4) to 6) for all the elements.
8) If me = 0, then not a single element have yielded, go to next load level.
9) If me > 0, then check for convergence using following displacement criteria,

where, ed = displacement norm, qi = total displacement at the ith iteration and ui−1 = total displacement at the 
If the convergence criterion is satisfied, then apply next load increment. If a convergence criterion is not satisfied then repeat the procedure from step 1) to step 9), till the displacements are converged.
Figure 2. Nonlinear algorithm for elasto-plastic analysis.
4. Validation
For validation, the field data reported by Gabr et al. [12] and Ismael and Klym [13] are used. A detailed geotechnical investigation of the soil at Canons Park site (England) was carried out as reported by Gabr et al. [12] . The soil profile consisted of stiff slightly gravelly fissured London clay to the depth of 4 m. The test pile, 0.17 m in diameter, was bored cast in place with an embedment length of 4.5 m. Cohesion of the soil linearly increased with depth at the rate of 10 kPa/m, with a value of 45 kPa at ground level. The EI value of the pile was 1500 KNm2. Soil was assumed to follow von-Mises yield criterion. Measured versus predicted lateral-pile response is presented in Figure 3 along with 3-D FEM prediction by Dewaikar et al. [14] . A reasonably good agreement is observed at lower load levels. But the difference at higher load level suggests to adopt different yield criterion. von-Mises yield criterion is independent of hydrostatic stress which resulted discrepancy at higher load level. So in the present study, Drucker-Prager and Mohr-Coulomb yield criterion are employed.
Comparison with pile load test data reported by Ismael and Klym [13] at Ontario is presented in Figure 4. A concrete pile with diameter 60 in (1.52 m) was embedded in over-consolidated clay with cohesion 2000 lb/ft2 (96.0 kPa). Total pile length was 39 ft (12.0 m) with one foot (0.30 m) length above ground-line. The flexural rigidity EI of pile was 93 × 1010 lb-in2 (2.675 × 106 kN∙m2). Comparison between measured and predicted pile response shows a good agreement at higher load levels.
Figure 3. Validation with experimental results [12] .
Figure 4. Validation with experimental results [13] .
5. Parametric Study
A parametric study is carried out to examine the effect of pile spacing and pile group configuration on static nonlinear response of pile groups (pile diameter D = 1.0 m, L/D ratio = 20). Six different pile group configurations (Figure 5) are considered as 2 × 2, 3 × 3, 3PP, 3PS, 2PP, 2PS (PP―piles in parallel arrangement, PS―piles in series arrangement). The pile is assumed linear elastic throughout the analysis and soil is modeled using von Mises yield criteria. The lateral force H = 2000 kN is applied at top. The values of the various parameters assumed for pile and soil in this study are summarized in Table 1.
5.1. Effect of Yield Criteria
An attempt has been made to study, the response of 2 × 2 pile group configuration using different yield criteria. In the present study three yield criteria have been used viz. von Mises (vM), Drucker-Prager and Mohr-Coulomb yield criteria. All the three forms of Drucker-Prager yield criteria have been included i.e. Drucker-Prager yield surface passing through inner (DP-I) and outer (DP-2) apices of Mohr-Coulomb yield surface and with plain strain condition (DP-3). Two forms of Mohr-Coulomb yield criteria based on the modifications suggested to overcome singularity by Owen and Hinton [10] and Sloan and Brooker [9] . These are represented by MC-1 and MC-2, respectively.
Figure 6 shows the variation of displacements with load using different yield criteria for 2 × 2 pile group configuration for L/D = 20, s/D = 2, 
Table 1. Pile and soil properties for parametric study.
Figure 5. Arrangements of pile in different pile group configurations.
Figure 6. Variation in load-displacement response with yield criteria.
load levels between about 800 kN to 1800 kN, vM yield criteria predicted higher response as compared to DP-1 and DP-3. This may be due to the fact that the effect of confining pressure is included in the Drucker-Prager yield criteria.
5.2. Effect of Pile Group Configuration
Figure 7 shows the variation of displacement with load for different configurations of pile groups with L/D = 20, D = 1.0 m and Es = 20,000 kPa, s/D = 2 and 7. Pile top displacements for maximum load are summarized in Table 2 for comparison. In case of pile in series and parallel configurations, series configurations are having higher displacements as compared to parallel configuration. This may be attributed to more passive resistance available in parallel arrangement. Among all the configurations 2PS group has highest displacement at all the load levels and 3 × 3 pile group has lowest displacements. It is obvious that the stiffness offered by pile cap is higher in series arrangement as compare to parallel arrangement, due to which in case of linear response the series arrangements are undergoing smaller displacements at small to medium L/D ratio. At pile spacing 2D, maximum displacement is observed to be 118.18 mm for pile group 2PS and 94.16 mm for pile group 2PP. It shows that 2PS configuration predicted 25.5% higher displacements as compared to 2PP configuration. Similar trend is observed in 3PS and 3PP configurations. At pile spacing 7D there is no considerable difference in the observed displacements for 2PS and 2PP configuration. Similar observations are made for the 3PS and 3PP configuration. At higher spacing overlapping of stress zone will be minimum and nearly full passive resistance is available. So soil will offer nearly equal resistance in series and parallel arrangement.
In the square configuration 2 × 2 pile group predicted higher displacements at all the load levels as compared to 3 × 3 pile group. Nonlinear maximum displacement is observed to be 11.57 mm in 3 × 3 configuration for pile spacing 2D. It is 25.6% higher than the linear displacement whereas nonlinear maximum displacement is 40.13 mm in 2 × 2 pile group configuration, which is 166.8% higher than the linear displacement. Combined structural stiffness of pile and pile cap in square arrangement is considerably higher than those groups in series or parallel arrangement. Owing to this, they will have smaller displacements for the same load level. Obviously, 3 × 3 pile group is much stiffer than 2 × 2 pile group.
To compare the effect of pile group configuration on a common basis, load-displacement relationships are normalized as explained previously. Load-displacement relationships in normalized form are presented in Figure 8 (s/D = 2). It is observed that relationship is linear up to normalized load level of 0.1 (except 3 × 3 pile group). Effect of nonlinearity is increasing with number of piles in pile group. But for same number of piles, parallel configurations are stiffer than series configurations due to availability of more passive resistance.
Figure 7. Load-displacement comparison for different pile group configurations.
Table 2. Linear and nonlinear response for different pile group configurations.
Figure 8. Normalized load-displacement response for different pile group configurations.
6. Concluding Remarks
A finite element program has been developed to perform the static nonlinear analysis of pile group with six different configurations subjected to lateral loads. A brief description of the numerical algorithm and its features has been presented. The pile has been assumed to remain elastic all the time whereas the soil has been assumed to undergo plastic yielding following von Mises yield criterion. The formulation of elasto-plastic analysis following von Mises yield criterion has been explained. The effect of Drucker-Prager and Mohr Coulomb yield criteria on the response of pile group is also investigated. The whole analysis is based on incremental load application. The external load is applied in small increments and the stresses are initially computed assuming elastic constitutive relation. These stresses in the soil elements are then checked against the corresponding yield criteria and are adjusted to satisfy the required conditions. The excess stresses are applied back again in the form of residual forces in the next iteration. This procedure is continued until a satisfactory convergence is arrived at. Significant effect of soil nonlinearity is observed at smaller pile spacing which reduces with increase in spacing. Combined structural stiffness of pile and pile cap in square arrangement is considerably higher than that of those groups in series or parallel arrangement.
Cite this paper
V. A.Sawant,K. B.Ladhane, (2016) Nonlinear FEA of Pile Group Subjected to Lateral Load. Open Journal of Civil Engineering,06,19-30. doi: 10.4236/ojce.2016.61003
References
- 1. Randolph, M.F. (1981) The Response of Flexible Piles to Lateral Loading. Géotechnique, 31, 247-259.
http://dx.doi.org/10.1680/geot.1981.31.2.247 - 2. Muqtadir, A. (1984) Three-Dimensional Nonlinear Soil-Structure Interaction Analysis of Pile Groups and Anchors. Ph.D. Thesis, Department of Civil Engineering and Engineering Mechanics, University of Arizona, Tucson, Arizona.
- 3. Muqtadir, A. and Desai, C.S. (1986) Three-Dimensional Analysis of Pile-Group Foundation. International Journal for Numerical and Analytical Methods in Geomechanics, 10, 41-58.
http://dx.doi.org/10.1002/nag.1610100104 - 4. Najjar, Y.M. and Zaman, M.M. (1986) Three-Dimensional Nonlinear Behavior of Pile Group Foundation: Effect of Loading Sequence. Annual Meeting of the OAS, Tahlequah, 14 November 1986.
- 5. Najjar, Y.M. and Zaman, M.M. (1988) Effect of Loading Sequence and Soil Nonlinearity on the Response of a Pile Group Foundation Using a Three-Dimensional Finite Element Analysis. Proceedings of the 6th International Conference on Numerical Methods in Geomechanics, Innsbruck, 11-15 April 1988, 1127-1134.
- 6. Ladhane, K.B. and Sawant, V.A. (2016) Effect of Pile Group Configurations on Nonlinear Dynamic Response. International Journal of Geomechanics, 16.
http://dx.doi.org/10.1061/(asce)gm.1943-5622.0000476 - 7. Viladkar, M.N., Noorzaei, J. and Godbole, P.N. (1995) Convenient Forms of Yield Criteria in Elasto-Plastic Analysis of Geological Materials. Computers & Structures, 54, 321-337.
http://dx.doi.org/10.1016/0045-7949(94)E0199-C - 8. Drucker, D.C. and Prager, W. (1952) Soil Mechanics and Plastic Analysis on Limit Design. Journal of applied Mathematics, 10, 157-165.
- 9. Sloan, S.W. and Booker, J.R. (1986) Removal of Singularities in Tresca and Mohr-Coulomb Yield Functions. Communications in Applied Numerical Methods, 2, 173-179.
http://dx.doi.org/10.1002/cnm.1630020208 - 10. Owen, D.R.J. and Hinton, E. (1980) Finite Element Programming in Plasticity. Pineridge Press Limited, Swansea, UK.
- 11. Nayak, G.C. and Zienkiewicz, O.C. (1972) Convenient Forms of Stress Invariants for Plasticity. Proceedings of the ASCE Journal of the Structural Division, 98, 949-953.
- 12. Gabr, M.A., Lunne, T. and Powell, J.J. (1994) p-y Analysis of Laterally Loaded Piles in Clay Using DMT. Journal of Geotechnical Engineering, 120, 816-837.
http://dx.doi.org/10.1061/(ASCE)0733-9410(1994)120:5(816) - 13. Ismael, N.F. and Klym, T.W. (1978) Behaviour of Rigid Piers in Layered Cohesive Soils. Journal of Geotechnical Engineering, 104, 1061-1074.
- 14. Dewaikar, D.M., Verghese, S., Sawant, V.A. and Chore, H.S. (2007) Non-Linear 3-D FEA of Laterally Loaded Pile Group Incorporating No-Tension Behaviour of Soil. Indian Geotechnical Journal, 37, 174-189.















