Open Journal of Civil Engineering
Vol.05 No.01(2015), Article ID:53914,11 pages
10.4236/ojce.2015.51003
A New Stiffness Matrix for a 2D-Beam Element with a Transverse Opening
Musab Aied Qissab
Department of Civil Engineering, Al-Nahrain University, Baghdad, Iraq
Email: musstruct@nahrain-eng.org
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 January 2015; accepted 6 February 2015; published 10 February 2015
ABSTRACT
Transverse opening in a beam has a reducing effect of the beam stiffness which will cause a significant increase in beam deflection in the region on the opening. In this paper, a new stiffness matrix for a beam element with transverse opening including the effect of shear deformation has been derived. The strain energy principle is used in the derivation process of the stiffness matrix and the fixed-end force vector for the case of a concentrated or a uniformly distributed load is also derived. The accuracy of the obtained results based on the derived stiffness matrix is examined through comparison with that of the finite element method using Abaqus package and a previous study which show a good agreement with high accuracy.
Keywords:
Stiffness Matrix, Transverse Opening, Shear Deformation, Inflection Point

1. Introduction
In general, transverse openings are made in beams to allow the passage of the service lines through the structure. Depending on the size and location, opening may reduce flexural stiffness of the beam significantly which will cause an increase in beam deflection as well as a decrease in strength of the beam. When a large opening is located near the support of a beam, the shear stiffness is reduced significantly and the deflection is highly increas- ed in the opening region which will make the beam serviceability unacceptable if it is not taken into account.
There are a limited number of studies that deal with the formulation of stiffness matrix of a beam with a transverse opening or deflection calculation of such beams. Benitez et al. [1] presented procedures for calculating deflection of composite beams with web openings that utilized matrix analysis method. Web opening was simplified and modeled using beam elements connected by rigid links. The analysis considered only the region around the opening assuming the small moment end of the opening to be fixed while the other was assumed to be free for rotation and deflection. The matrix analysis was used to calculate the deflection across the opening only and the results was utilized to derive equations for the total deflection calculation.
Donghua et al. [2] derived formulas for determining deflection of simply supported steel I-beams with a web opening. The formulas were derived by direct solving of differential equations combined by using displacement method. The solution was limited to two loading cases only: a concentrated load at mid span and a uniformly distributed load along the span. The shear deformation was not considered.
The main objective of this paper is to derive an accurate stiffness matrix and a fixed-end force vector for a beam with transverse opening that are useful and simple for matrix analysis and software applications.
2. Statement of the Problem
Consider a two dimensional (2D) beam element with a transverse opening as shown in Figure 1. The imperforated segments of the beam are assumed to be connected by upper and lower beams in the opening region which have a flexural rigidity of EIt and EIb respectively.
To simplify the derivation of stiffness matrix, it is assumed that the bending moment in the opening region consists of two parts: primary and secondary moments. The primary moment is caused by the normal tension-compression forces couple acting on the section which has a little effect on the total deflection while the secondary moment is caused by the shear force acting on the upper and lower beams. The secondary moment cause a significant increase in deflection in the opening region as shown in Figure 1. Also, it is assumed that an inflection points are located at the midpoint of the upper and lower beams in the opening region which is utilized to find the secondary moment in the opening region. The previous assumptions have been verified through the finite element analysis carried out in this paper. The assumptions were adopted by Donghua et al. [2] .
The stiffness coefficients have been found by using Castigliano’s second theorem Boresi and Schmidt [3] , which states that the deflection caused by an external force is equal to the partial derivative of the total strain energy (UT) with respect to that force. The total strain energy caused by bending, axial, and shear forces can be written respectively as follows:
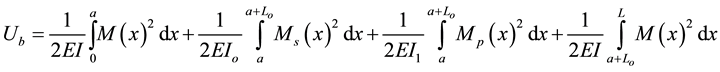 (1)
(1)
 (2)
(2)
 (3)
(3)
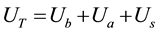 (4)
(4)
in which
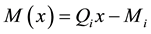 (5)
(5)
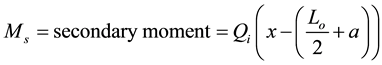 (6)
(6)
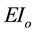 = flexural rigidity of the upper and lower beams at the opening considering the bending of each beam individually due to the secondary moment;
= flexural rigidity of the upper and lower beams at the opening considering the bending of each beam individually due to the secondary moment;
 (7)
(7)
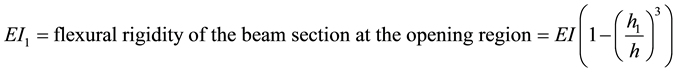 (8)
(8)
 (9)
(9)
Figure 1. Beam element with a transverse opening: (a) Nodal forces and degrees of freedom; (b) Deflected shape.
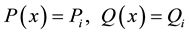
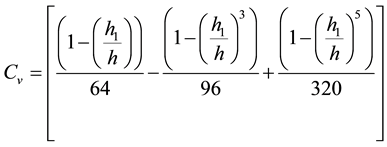 (10)
(10)
A = cross-sectional area of the imperforated beam, h = total depth of the beam, b = with of the beam, h1 = depth of the opening, G = shear modulus, E = elastic modulus. After simplifications, carrying out the necessary integrals, and substituting the above expressions into Equation (4), the following expression for the total strain energy can be given:
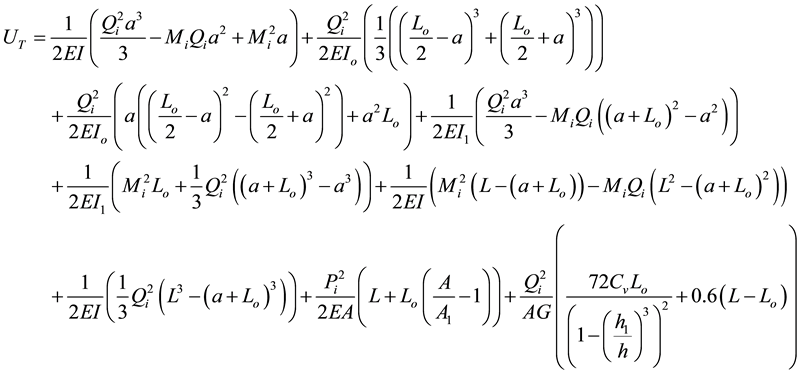 (11)
(11)
The partial derivative of the total strain energy with respect to Pi, Qi, and Mi is equal to the corresponding nodal displacements which can be given as follows:
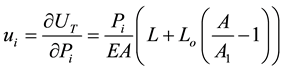 (12)
(12)
 (13)
(13)

where



2.1. Axial Stiffness
The axial stiffness coefficients can be found by setting the axial nodal displacement equal to (1) with all other displacements equal to zero (i.e.




The axial force at node (j), (Pj), can be found from equilibrium condition. Accordingly,

2.2. Translational Stiffness
The translational stiffness coefficients corresponding to a unit translational displacement at node (i), (vi), can be found by equating the translational nodal displacement equal to (1) with all other displacements equal to zero (i.e.





Solving the above equation for Pi, Qi, and Mi, the following stiffness coefficients can be obtained:

Similarly, from equilibrium, the following stiffness coefficients can be given:

2.3. Rotational Stiffness
In the same previous procedure, the rotational stiffness corresponding to a unit rotation at node







The rotational stiffness coefficients can be given as follows:

From equilibrium,

Making use of the symmetry of the stiffness matrix and from equilibrium requirements, the other stiffness matrix coefficients can be obtained as follows:















The (6 × 6) stiffness matrix can be written as follows:

3. Fixed-End Forces for a Beam with a Transverse Opening Due to a Concentrated Load (P)
Consider a fixed-end beam with a transverse opening is acting upon by a concentrated load (P) as shown in Figure 2.
Making use of superposition and the condition that the sum of nodal displacements in each direction must equal to zero at the fixed end and neglecting the effect of axial deformation (i.e.

where


Figure 2. Fixed-end beam with a transverse opening under a concentrated load.


in which





for

for

for

Solving Equation (47) for QFi, MFi yields the following:

4. Fixed-End Forces for a Beam with a Transverse Opening Due to a Uniformly Distributed Load (W)
Consider a fixed-end beam with a transverse opening is acting upon by a concentrated load (W) as shown in Figure 3.
Following the same previous procedure, the following expressions for 



Substituting Equations (48), (57) and (58) into Equation (56) the values of QFi and MFi for a uniformly distributed load (W) can be obtain.
5. Numerical Examples
To examine the correctness of the derived stiffness matrix and the fixed-end force vectors, the simply supported steel I-beam shown in Figure 4. (which was previously analyzed by Donghua et al. [2] ) is analyzed under two loading cases; a concentrated load and a uniformly distributed load. The obtained results are compared with that obtained by Donghua et al. [2] which are shown in Figure 5 and Figure 6 and a good agreement is obtained.
Another verification for the obtained results is made by the finite element analysis of the same beam using Abaqus package [4] . The (C3D8IH) 8-node linear brick, hybrid, linear pressure, incompatible modes element is used in the finite element analysis. The finite element mesh of the beam is shown in Figure 7. The deformed shape of the beam for the two loading cases is shown in Figure 8 and Figure 9 and the results are shown in Figure 10 and Figure 11. The present finite element analysis shows a good agreement with the obtained results using the derived matrix and the fixed-end force vectors.
Figure 12 and Figure 13 show the effect of shear deformation for the two loading cases and it is found that the maximum increase in deflection due to shear deformation is (6.96%) at midspan of the beam under the concentrated load. The increase in deflection is (4.48%) at midspan of the beam under the uniformly distributed load.
Figure 3. Fixed-end beam with a transverse opening under a uniformly distributed load.
Figure 4. Steel I-beam with a transverse opening under two loading cases.
Figure 5. Beam deflection profile of the present analysis versus Donghua et al. [2] analysis (concentrated load).
Figure 6. Beam deflection profile of the present analysis versus Donghua et al. [2] analysis (uniformly distributed load).
Figure 7. Finite element mesh of the beam under consideration.
Figure 8. Deformed shape of the beam under the action of a concentrated load.
Figure 9. Deformed shape of the beam under the action of a uniformly distributed load.
Figure 10. Beam deflection profile of the present analysis versus finite element analysis (concentrated load).
Figure 11. Beam deflection profile of the present analysis versus finite element analysis (uniformly distributed load).
Figure 12. Beam deflection profile of the present analysis showing the shear deformation effect (concentrated load).
Figure 13. Beam deflection profile of the present analysis showing the shear deformation effect (uniformly distributed load.
6. Conclusions
In this article, a new stiffness matrix and fixed-end force vectors for a 2D-beam element have been derived including the effect of shear deformation. It has been found that the existence of the opening enlarges the maximum
deflection of the beam significantly for the studied cases. The ratio of the maximum deflection (at the opening region) to the maximum deflection of the solid beam (no opening) is 3.32 for the case of a concentrated load at midspan and 4.39 for a uniformly distributed load. This is due to the effect of secondary moments acting on the upper and lower beams at the opening region. The maximum ratio for the increase in deflection due to the effect of shear deformation is found in the range of 4.48% - 6.96% for the cases under consideration. Through the verification of results, a good agreement has been observed between the obtained results and that obtained from the finite element analysis in addition to that available in the literature. The derived stiffness matrix and the fixed-end force vectors are useful and simple to use in the matrix structural analysis packages.
References
- Benitez, M.A., Darwin, D. and Donahey, R.C. (1990) Deflection of Composite Beams with Web Openings. A Report on Research, University of Kansas, Lawrence.
- Donghua, Z., Longqi, L., Jürgen, S., Wolfgang, K. and Peng, W. (2012) Elastic Deflection of Simply Supported Steel I-Beams with a Web Opening. International Conference on Advances in Computational Modeling and Simulation. Procedia Engineering, 31, 315-323.
- Boresi, A.P. and Schmidt, R.J. (2003) Advanced Mechanics of Materials. 6th Edition, Wiley, New York.
- (2009) Abaqus Theory Manual. Dassault Systèmes Simulia Corp. Providence.














