Open Journal of Civil Engineering
Vol. 3 No. 2A (2013) , Article ID: 33115 , 9 pages DOI:10.4236/ojce.2013.32A003
Non-Linear Analysis of Masonry Structures Subjected to External Settlements
Department of Architecture, University of Florence, Florence, Italy
Email: stefano.galassi@unifi.it
Copyright © 2013 Stefano Galassi et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 30, 2013; revised June 2, 2013; accepted June 12, 2013
Keywords: Masonry; Arches; Walls; Ruins; Settlements; Internal Distortions; Non-Linear Analysis
ABSTRACT
This article describes a methodology for the non-linear analysis of existing masonry structures subjected to external yielding constraints, with particular attention to the historical and cultural heritage constructions. It is well known, indeed, that most of the arch and wall damages are often due to settlement of abutments, in the former case, and to settlement of foundations, in the latter one. The ability to observe and correctly analyze the cracking failure pattern, visible on such structures, is the main “diagnostic tool” for identifying its origin: the modification of load conditions over time, foundation settlements and earthquakes. The objective of this work is to identify a numeric modelling of masonry structures (such as walls, arches, vaults, ruins) under any load condition and subjected to inelastic settlements impressed to some external constraints. The purpose of the numerical procedure is to interpret the behaviour of such structures in order to assess both the peak settlement value and their specific failure mode in correspondence to a geometry which is very often compromised. Therefore, this procedure allows one to estimate the degree of the structures’ vulnerability, in order to prevent any future damage, both local and global. The iterative algorithm proposed in this article, developed in a calculation software, processes the structure considering, not only the properties of constitutive material, non-homogeneous and anisotropic, but also the change of the structure’s shape during the settlements increase. In this way a non-linear analysis is performed both materically and geometrically. Through a direct comparison between numerical and experimental results, obtained by testing some simple structural models in a laboratory, it was ascertained, both from a qualitative and quantitative point of view, the correctness and the efficacy of the proposed procedure, which will be explained below. Therefore, this numerical procedure demonstrates to be a useful “diagnostic tool” by which, starting from the input of the masonry structure to be studied and simulating a presumable event, one can trace the source of the causes that have generated a certain failure, comparing the cracking pattern of real structure with that plotted by the software.
1. Introduction
A masonry structure is analyzed by means of a discrete model, previously proposed in other works, according to the early static theories of the mid-1700’s describing the behaviour of masonry arches. Such a model is still considered by J. Heyman [1], in his basic studies about masonry arch stability, as an appropriate and correct method to expound the general behaviour of masonry structures. Many experimental surveys, as well as the observation of the “real behaviour” of masonry constructions subjected to different kind of external actions, clearly highlighted the dependence of collapse mechanisms [2] on the loss of local strength due to the separation of the masonry elements, considering these both as single blocks and a series of blocks forming wider portions of masonry, that is composed of a certain number of elements which have not lost their mutual cohesion.
Moreover, according to such a model, the shape of single blocks does not change when external loads are applied, so as their rigid displacements, due to detachments and/or sliding along the joints, which the contact devices allow, are prevailing in comparison with the deformability of the whole structural system. The main features of such a model consist of the inner coherence of the blocks and the presence of “discontinuity” surfaces along which such a coherence may also not be respected: the constitutive material is not able to support tensile stresses along the surfaces where its “inner structure” is detached, while it is coherent with and uncompressible in the other parts. Under these assumptions, the mechanical characterization of masonry, that is its generic constructive configuration, being both an arch and a wall, refers to a system of rigid blocks connected by unilateral contact and frictional [3] links. Moreover, relying on the general potentiality of such an approach, it is reasonable to think that a model which considers the rigid blocks linked together by means of non-deformable or deformable surfaces, no tension and enriched by friction, is the most correct model to interpret the influences which have the greatest effect on the dimensions of the blocks, the joints’ orientation [4] and the apparatus itself on the behaviour of historical masonry buildings.
2. The Contact Constraint Device
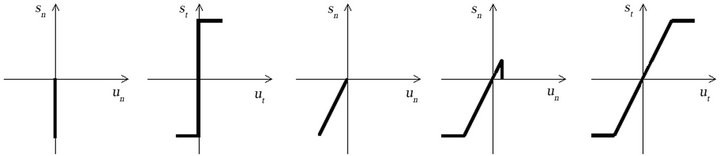
As previously stated, the peculiar characteristic of the discrete model is the description of the masonry building by means of a rigid system in which the elasticity is totally thought to be concentrated in the mortar joints (such an approach has been proposed and developed in several works by the authors themselves [5], as well as in scientific articles of other authors [6,7]). The hypotheses about the behaviour of the “material” are widely described through a suitable contact device (Figure 1), taking advantage of the use of an algebraic system of equations to write the structural problem mathematically. In this sense, assuming the structure is dry assembled or built with a large quantity of spoiled mortar, it will be possible to consider a unilateral and frictional contact link (brittlerigid contact device—Figures 2(a) and (b)); otherwise, if the mortar is very effective, the joint behaviour will be characterized by an elastic unilateral link. Furthermore, it will be possible to transfer the shear forces, which should not exceed any assigned value (elastic-cracking contact device—Figures 2(c) and (e)). In the latter case, it is important, from both a physical and numeric point of view, to consider a weak tensile strength instead of the complete absence of tensile strength, defining its limit value (Figure 2(d)).
The first model is designed to do a limit analysis of the structures; the second one, instead, for a kind of analysis which is able to furnish the actual stress state inside the structure, the position of the failure interfaces and also identify the shape and dimensions of the cracks.
Thus, the contact devices are described by a set of fictitious links, arranged orthogonal to the interface surfaces, capable of transmitting only compressive forces or, at most, weak tensile forces which do not exceed the assigned limit values, and, by an additional link, tangent to the interface surface, to transmit the shear force. In case of brittle-rigid joint only two normal links are strictly necessary. In the case of elastic-cracking joint it is better to consider at least four normal links in order to highlight the actual cracking pattern with the possibility of measuring the width and depth of the cracks inside the mortar joints.
3. General Formulation of the Problem
Let us consider, therefore, the general problem of any masonry structure composed of a finite number of rigid blocks which are dry assembled or mortar layered. The system composed of n blocks and m interfaces, subjected to a load condition (represented by vector F) and inelastic displacements (represented by vector Δ) which are only located in the external joints, can be expressed through a system of equilibrium and elastic-kinematical equations, as follows:
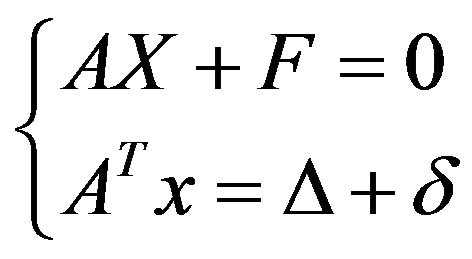 sub
sub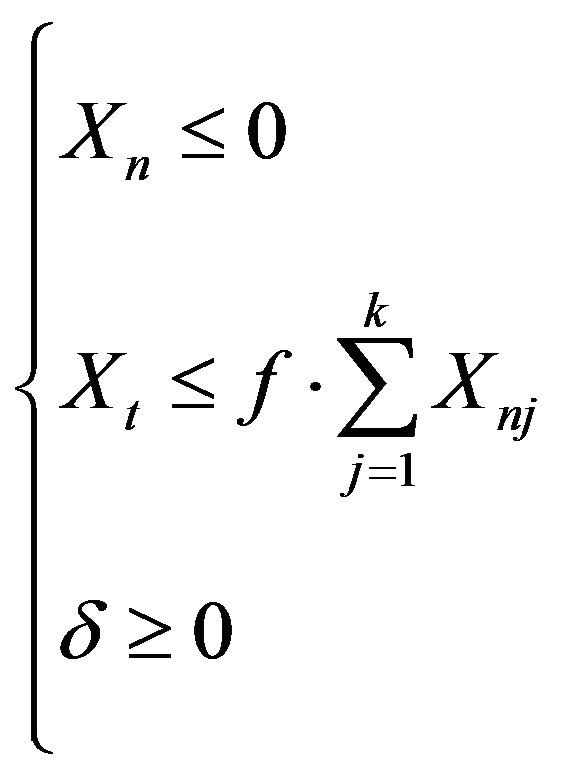 , (1)
, (1)
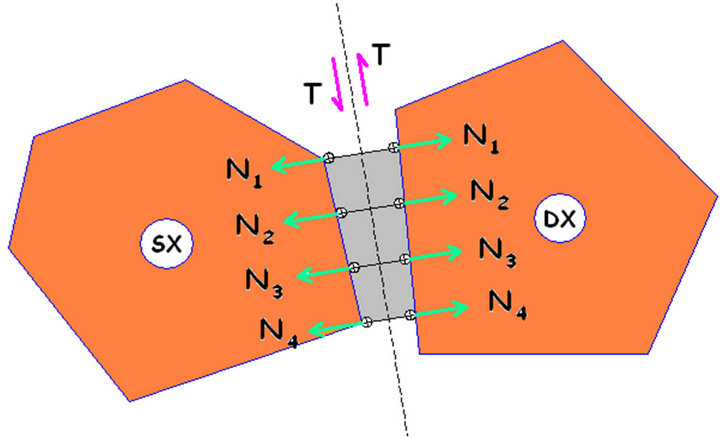
Figure 1. Discrete model of the interface joint.
 (a) (b) (c) (d) (e)
(a) (b) (c) (d) (e)
Figure 2. Behaviour of the interface joints: brittle-rigid joint in normal direction (a) and tangential (b) elastic-cracking joint in normal direction (c) or (d) and tangential (e).
in the case of brittle-rigid contact joint, and:
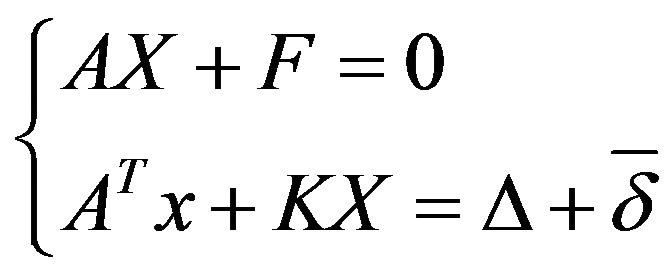 sub
sub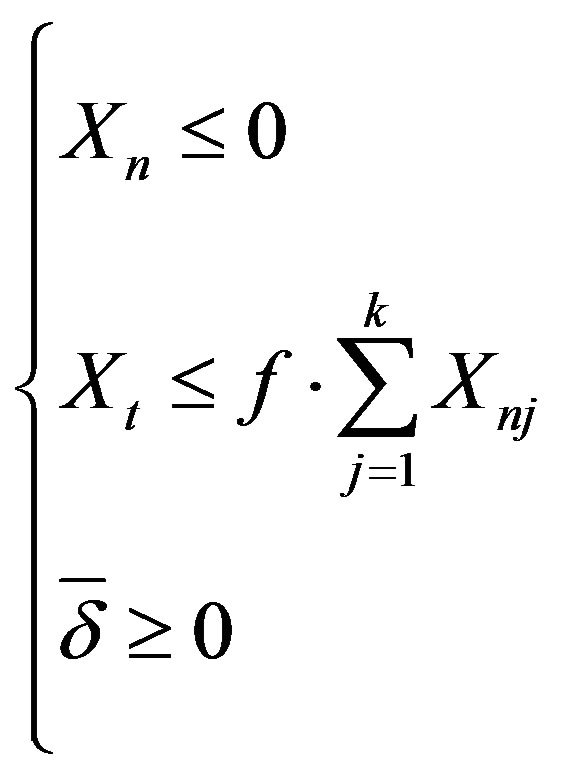 , (2)
, (2)
in the case of elastic-cracking contact joint.
In Equations (1) and (2) the coefficients of the subvectors 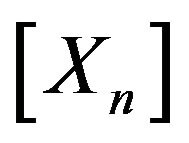 and
and  of vector
of vector 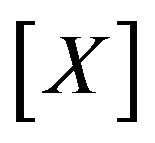 represent the unknowns of the interface interactions related to the normal forces and to the tangential ones, to which the in equalities [8], written to respect the hypotheses related to the constitutive model of the joint, correspond (above all, the second inequality makes it possible to introduce a suitable friction coefficient
represent the unknowns of the interface interactions related to the normal forces and to the tangential ones, to which the in equalities [8], written to respect the hypotheses related to the constitutive model of the joint, correspond (above all, the second inequality makes it possible to introduce a suitable friction coefficient 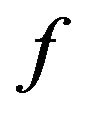 [9] in correspondence to the joints described through an assigned number
[9] in correspondence to the joints described through an assigned number 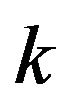 of normal links); the components of vector [
of normal links); the components of vector [![]() ] represent the unknown displacements of the blocks’ centroids. The coefficients of matrix [
] represent the unknown displacements of the blocks’ centroids. The coefficients of matrix [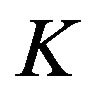 ], presented only in the second equation of (2), represent the deformability of the links which describe the mortar elastic joint. The proposed algorithm [10,11] makes use of internal impressed distortions, according to Colonnetti’s theorem [12], which states that any stress state can be suitably modified by introducing ad-hoc distortions whose number cannot exceed the degree of static indeterminacy of the structure. In the case of brittle-rigid joints, when tensile forces are higher than the limit values, the distortions’ vector [
], presented only in the second equation of (2), represent the deformability of the links which describe the mortar elastic joint. The proposed algorithm [10,11] makes use of internal impressed distortions, according to Colonnetti’s theorem [12], which states that any stress state can be suitably modified by introducing ad-hoc distortions whose number cannot exceed the degree of static indeterminacy of the structure. In the case of brittle-rigid joints, when tensile forces are higher than the limit values, the distortions’ vector [![]() ] must be computed in such a way that the tensile forces become equal to zero and the shear forces became equal to the limit friction force. In the case of elastic-cracking joints, the distortions vector, expressed as the notation
] must be computed in such a way that the tensile forces become equal to zero and the shear forces became equal to the limit friction force. In the case of elastic-cracking joints, the distortions vector, expressed as the notation , is calculated in such a way that the sub-vector [
, is calculated in such a way that the sub-vector [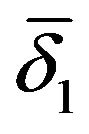 ] (as in the case of brittle-rigid joint) must transform the tensile forces so they become equal to zero and the shear forces become equal to the limit friction force, while sub-vector [
] (as in the case of brittle-rigid joint) must transform the tensile forces so they become equal to zero and the shear forces become equal to the limit friction force, while sub-vector [ ] only has to modify some of the displacement components so as to obtain a solution capable of satisfying both the equilibrium equations, while respecting the sign conditions, and the elastickinematical compatibility of the actual reacting structure. The non-zero components of sub-vector [
] only has to modify some of the displacement components so as to obtain a solution capable of satisfying both the equilibrium equations, while respecting the sign conditions, and the elastickinematical compatibility of the actual reacting structure. The non-zero components of sub-vector [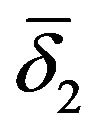 ] give the position and width of the cracks located in the contact joints.
] give the position and width of the cracks located in the contact joints.
4. The Numerical Procedure
Referring to both the former and to the latter kind of joints, the solution ( ) and the relevant distortions vectors [
) and the relevant distortions vectors [![]() ] or [
] or [ ] are computed by an iterative procedure whose starting point corresponds to the static solution obtained making use of the generalized inverse
] are computed by an iterative procedure whose starting point corresponds to the static solution obtained making use of the generalized inverse
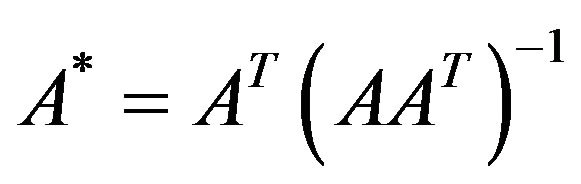 of the equilibrium matrix [
of the equilibrium matrix [ ], whose uniqueness was demonstrated by Moore-Penrose, in the case of brittle-rigid model; while in the elastic-cracking model, the starting point corresponds to the standard solution obtained assuming the material is linear-elastic and bilateral. Thus, in the case of the brittle-rigid joint, it is possible to write:
], whose uniqueness was demonstrated by Moore-Penrose, in the case of brittle-rigid model; while in the elastic-cracking model, the starting point corresponds to the standard solution obtained assuming the material is linear-elastic and bilateral. Thus, in the case of the brittle-rigid joint, it is possible to write:
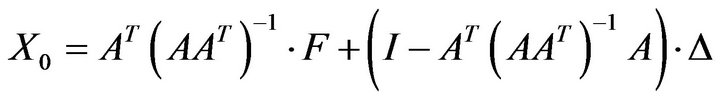 ; (3)
; (3)
while in the case of elastic-cracking joint the equation is:
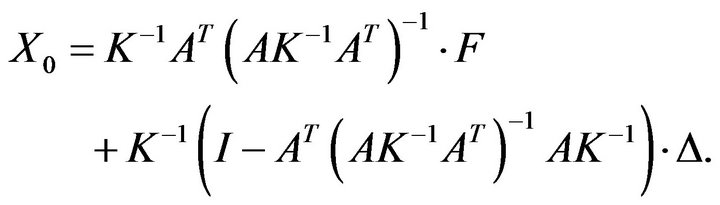 (4)
(4)
It is interesting to note that the initial solution [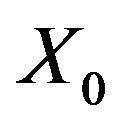 ], reached under the hypothesis of brittle-rigid joint, corresponds exactly to the initial solution obtained under the assumption of strained joint in the case where the strain matrix [
], reached under the hypothesis of brittle-rigid joint, corresponds exactly to the initial solution obtained under the assumption of strained joint in the case where the strain matrix [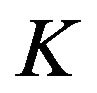 ] is replaced by the identity matrix, that is assuming a constant und unity stiffness of all the links present in the model of the structure.
] is replaced by the identity matrix, that is assuming a constant und unity stiffness of all the links present in the model of the structure.
Remembering that in the case of any compatible linear system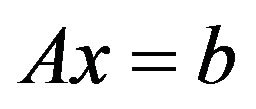 , the whole system of solutions is expressed by
, the whole system of solutions is expressed by , where
, where ![]() is an arbitrary vector suitably chosen while
is an arbitrary vector suitably chosen while 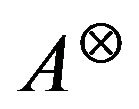 is any inverse able to satisfy the condition
is any inverse able to satisfy the condition 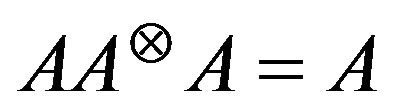 [13], in both hypotheses the final solution assumes the general form:
[13], in both hypotheses the final solution assumes the general form: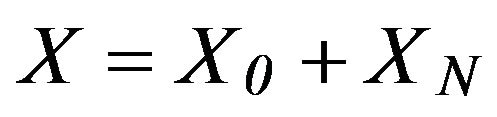 . In such a case:
. In such a case:
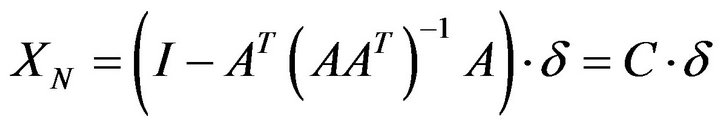 , (5)
, (5)
in the case of brittle-rigid joint, and:
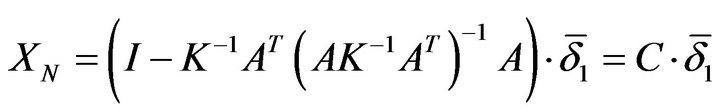 , (6)
, (6)
in the case of elastic-cracking joint.
The initial solution vector [ ] can result whenever it is coherent with the sign conditions expressed through the in Equalities (1) and (2): such a circumstance corresponds to the particular case of a masonry structure, subjected to any external action, whose joints are all compressed and satisfy the hypotheses about the friction. If any of the components of vector [
] can result whenever it is coherent with the sign conditions expressed through the in Equalities (1) and (2): such a circumstance corresponds to the particular case of a masonry structure, subjected to any external action, whose joints are all compressed and satisfy the hypotheses about the friction. If any of the components of vector [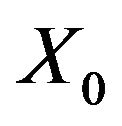 ] do not satisfy the imposed conditions, such a vector is then modified by an iterative procedure in which the choice of the suitable components of vector [
] do not satisfy the imposed conditions, such a vector is then modified by an iterative procedure in which the choice of the suitable components of vector [![]() ] or [
] or [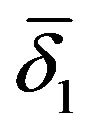 ] follows the criterion, step by step, in search for the link with the highest tensile value; the vectors themselves preserve the values previously assumed. Then, the iterative procedure goes on searching for the tangential link whose force is greater than the friction force [14]. In its iterative development, the algorithm follows the statement suggested by C. Alberto Castigliano in his study of the bridge over the Dora river built by Carlo Mosca, between 1823 and 1830, in Turin [15]. It is best to remember, as stated above in our comment about Colonnetti’s theorem, that the maximum number of possible iterations is equal to the degree of statically indeterminacy of the structure: this is the reason why it is not necessary to state further criteria to define the convergence of the algorithm. If the convergence has not been reached during the maximum number of possible iterative cycles, it is possible to state that, in dependence on the external action on the structure, there does not exist an equilibrium configuration which satisfies the hypotheses assumed for the behaviour of the material.
] follows the criterion, step by step, in search for the link with the highest tensile value; the vectors themselves preserve the values previously assumed. Then, the iterative procedure goes on searching for the tangential link whose force is greater than the friction force [14]. In its iterative development, the algorithm follows the statement suggested by C. Alberto Castigliano in his study of the bridge over the Dora river built by Carlo Mosca, between 1823 and 1830, in Turin [15]. It is best to remember, as stated above in our comment about Colonnetti’s theorem, that the maximum number of possible iterations is equal to the degree of statically indeterminacy of the structure: this is the reason why it is not necessary to state further criteria to define the convergence of the algorithm. If the convergence has not been reached during the maximum number of possible iterative cycles, it is possible to state that, in dependence on the external action on the structure, there does not exist an equilibrium configuration which satisfies the hypotheses assumed for the behaviour of the material.
The choice of an iterative procedure represents, de facto, an effectiveness shortcut to the actual difficulty in finding the number and the index of the components of the distortions vector through the mathematically direct withdrawing of the full rank sub-matrix from the algebraic operator [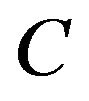 ], assuming it exists. To update the components of the distortions vectors, in both kinds of joint, the forms:
], assuming it exists. To update the components of the distortions vectors, in both kinds of joint, the forms: 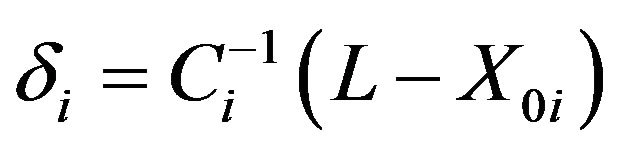 or
or
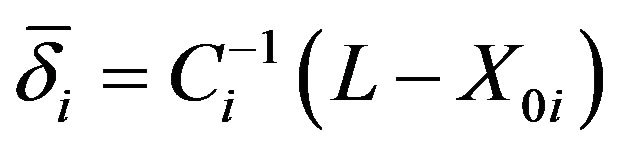 is used at every step; in which
is used at every step; in which 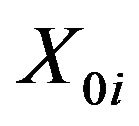
 indicates the vector whose components correspond to the internal forces in the joints which do not satisfy the conditions (1) and (2) above, while
indicates the vector whose components correspond to the internal forces in the joints which do not satisfy the conditions (1) and (2) above, while ![]() represents both the limit value for the tensile force in the normal links (L = 0) and the friction force for the tangential link
represents both the limit value for the tensile force in the normal links (L = 0) and the friction force for the tangential link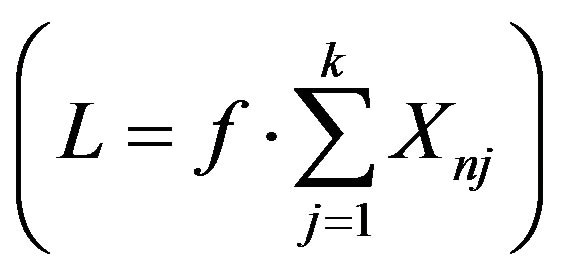 .
.
The final static solution of the numerical procedure will provide a final vector solution in the form:
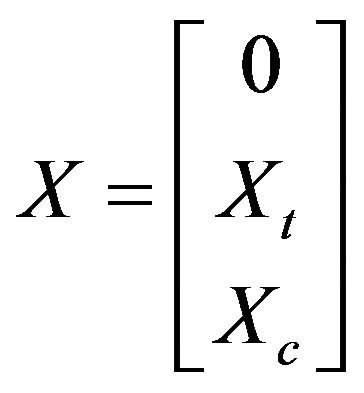 where, in correspondence of all the joints, it is:
where, in correspondence of all the joints, it is:
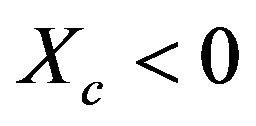 and
and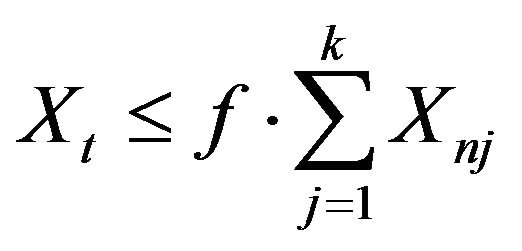 .
.
Such a solution, as computed above described, is the final one in the case of brittle-rigid joint and represents the limit equilibrium configuration of the structure. The nonzero components of vector [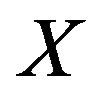 ] correspond to the portions of the joints which still preserve the mutual contact and through which the interactions, which agree with the assumed hypotheses, are transferred. On the contrary, the zero components identify the portions in which the contact has been lost.
] correspond to the portions of the joints which still preserve the mutual contact and through which the interactions, which agree with the assumed hypotheses, are transferred. On the contrary, the zero components identify the portions in which the contact has been lost.
In the case of strained joint, since the final vector [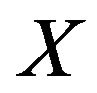 ] is generally different from the initial one [
] is generally different from the initial one [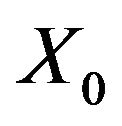 ], it is necessary to restore the elastic-kinematical compatibility expressed through the second equation of system (2), keeping in mind the actual detachments in the interfaces. To restore the compatibility easily, it is better to consider a partition of all the matrices related to the system of elastickinematical equations; only the indices of the links whose normal and tangential component agree with the sign conditions at the end of the iterative procedure are considered. In this case, the vector containing the displacements of the centroids of the blocks, corresponding to the actual reacting structure, and the vector [
], it is necessary to restore the elastic-kinematical compatibility expressed through the second equation of system (2), keeping in mind the actual detachments in the interfaces. To restore the compatibility easily, it is better to consider a partition of all the matrices related to the system of elastickinematical equations; only the indices of the links whose normal and tangential component agree with the sign conditions at the end of the iterative procedure are considered. In this case, the vector containing the displacements of the centroids of the blocks, corresponding to the actual reacting structure, and the vector [ ] which is able to restore the compatibility of the system, are obtained through the following equations:
] which is able to restore the compatibility of the system, are obtained through the following equations:
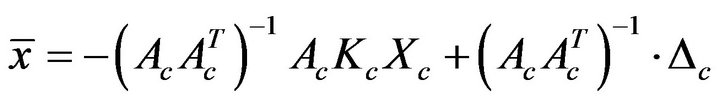 , (7)
, (7)
 , (8)
, (8)
where the non-zero components of vector [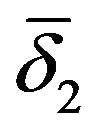 ] provide the position and the depth of the cracks.
] provide the position and the depth of the cracks.
5. The Case of the External Settlements
The above described calculation procedure, while operating within the intrinsic nonlinearity characterizing the general problem of structures with unilateral constraints, refers to the initial geometric configuration of the masonry structure used to formulate both the equilibrium and compatibility equations. Only at the conclusion of the analysis, starting from the initial configuration, it will be meaningful to define a modified configuration of the structure which considers the joint strains and the possible dislocations between elements due to the presence of fractures.
On the contrary, in the case of behaviour analysis of masonry structures subjected to external inelastic displacement constraints, assuming they are applied by finite values, the geometrical nonlinearity, deriving from the modification of the initial geometry due to the subsequent increase of such displacements, should also be considered.
With the aim of defining the degree of vulnerability of a masonry structure [16], which at the beginning is stable even if cracked, subjected to any load condition (a condition which could be verified through one of the mechanical models and the numerical procedure described above), it is significant to determine the peak value of the settlements which can be impressed in a specific point of the structure, beyond which the structure itself reaches the collapse due to the loss of equilibrium of a modified geometric configuration no longer suitable to support the initial loads.
The general procedure described in the previous paragraphs is still valid if considered inside a further process which depends on the subsequent increase of the nonzero components of vector [![]() ] of the inelastic settlements. At every step of such a procedure the general configuration matrix [
] of the inelastic settlements. At every step of such a procedure the general configuration matrix [ ] coefficients are updated as a function of the components of the displacements [
] coefficients are updated as a function of the components of the displacements [![]() ] of the centroids of the blocks obtained in the previous step of the analysis. So it is possible to write:
] of the centroids of the blocks obtained in the previous step of the analysis. So it is possible to write:
 . (9)
. (9)
Obviously such an equation can be used only in the case of structures whose joints are deformable [17], because in the case of structures whose joints are brittlerigid it is important to consider a modified configuration only when a structure, at the end of the analysis that defines its equilibrium configuration while respecting the sign conditions of the interface links, divides into blocks capable of forming an isostatic system, to which you can impose an external displacement capable of transforming the structure into a mechanism [18].
It is not difficult to single out as belonging to this latter case the simple arch structure made of stone blocks and placed in mutual contact without interposition of mortar, which is in an initial configuration of stable equilibrium. As it is known, any settlement, even if small, allocated in correspondence with one of the abutments [19] causes the formation of three instantaneous opening hinges: thus the structure assumes the typical isostatic configuration of a three hinge arch. Only now it is possible to imagine an increase of settlement and the formation of modified configurations, to be defined by means of a kinematical analysis related to large displacements (geometrical nonlinearity), to which the equilibrium condition [20] is checked each time.
6. Numerical Examples and Experimental Comparisons
In the following, some numerical examples of masonry structures subjected to external settlements are described. The former series refers to the simple case of an arch, composed of rigid blocks placed in mutual contact without the presence of elastic joints, initially stable under an imposed load condition (Figure 3). The analysis has been performed using the brittle-rigid model through which it is possible to obtain the position of the three opening hinges due to a suitably chosen incipit of the settlement of an abutment. Then, through the modification of the geometry due to the subsequent increase of the displacement obtained using the rules of the kinematical analysis in large displacements (geometrical nonlinearity), the above mentioned procedure has been used to check the state of equilibrium until the fourth hinge opens, showing the collapse of the structure. The numerical procedure, implemented in the software BrickWORK [21] suitably developed and equipped with a graphic output device for the real-time showing of the configurations assumed by the structure during the increase of the springing settlements, used for both the horizontal and vertical displacements, reproduces a few simple experiments carried out in the laboratory. The position of the interfaces affected by hinge openings, obtained numerically, corresponds exactly to the one detected in the experimental model. The precise correspondence between the experimental results and the numerical ones, relative to the definition of the peak set-
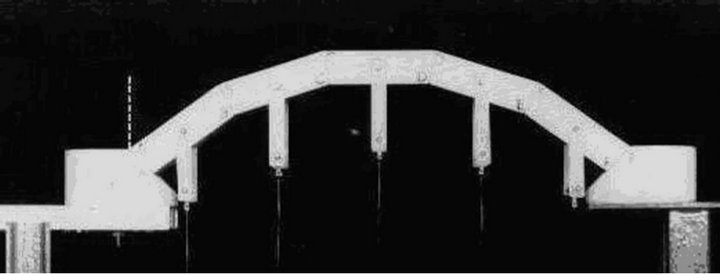


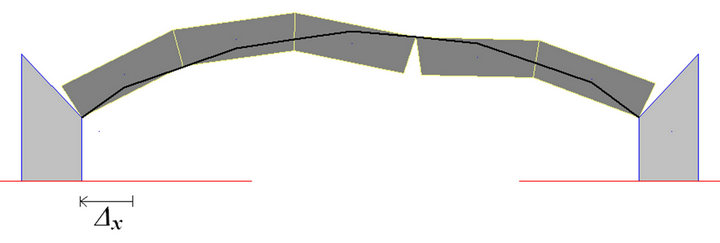
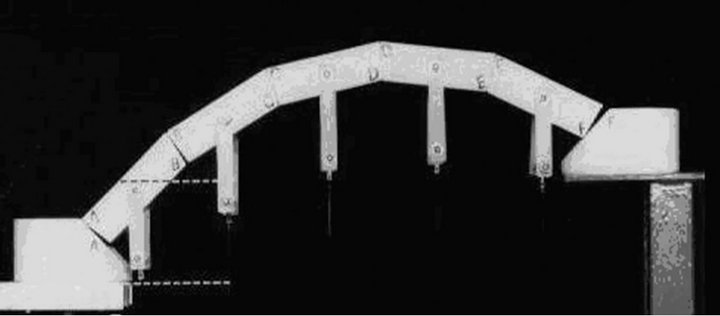

Figure 3. Arch subjected to imposed horizontal and vertical settlements. Comparison between the experimental model and the results obtained through the numerical procedure. Conditions immediately before the collapse of the structure.
tlement, for both cases is perfectly verified, with a slight decrease (not a significant percentage) of the values in the case of the actual model due, of course, to the inevitable imperfections of the model itself.
The solution obtained for the same cases using the calculation model with elastic-cracking joint (assuming in this case a joint of minimum thickness and with very low deformation) provides the same results as the previous solution, approaching even more to the experimental result. This is probably due to the minimum deformation assumed in the joints which, from a physical point of view, can be compared with the influence of imperfecttions present in the actual model.
The latter group of examples deals with the analysis of the behaviour of a series of voussoir arches, subjected simply to self-weight, for which the spam and the number of blocks have been left unchanged, while the average radius of curvature and the angle of sets have been progressively modified, so as to obtain a decreasing rise.
Using the calculation model with elastic-cracking interfaces assuming self-weights, elastic moduli of the joint and geometry (where and thick = 40 cm) compatible with a realistic condition, the peak horizontal settlements related to each configuration have been computed.
and thick = 40 cm) compatible with a realistic condition, the peak horizontal settlements related to each configuration have been computed.
Figure 4 shows the collapse configuration relative to one of the cases with the identification and the actual depth of the cracks.
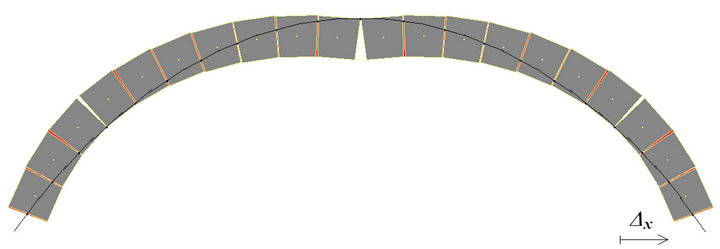

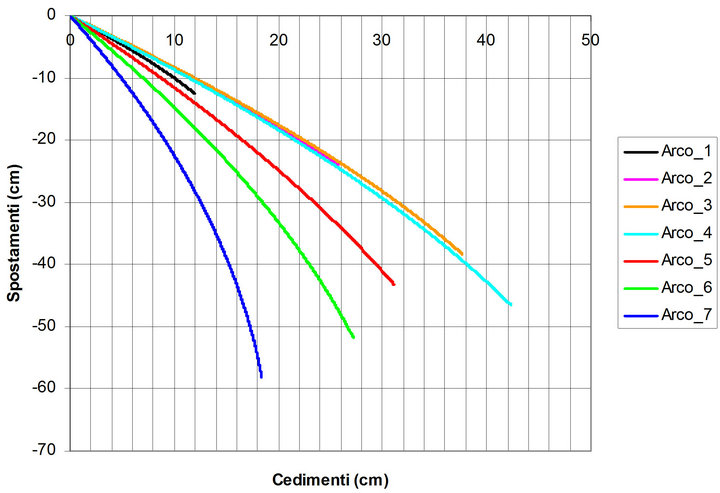

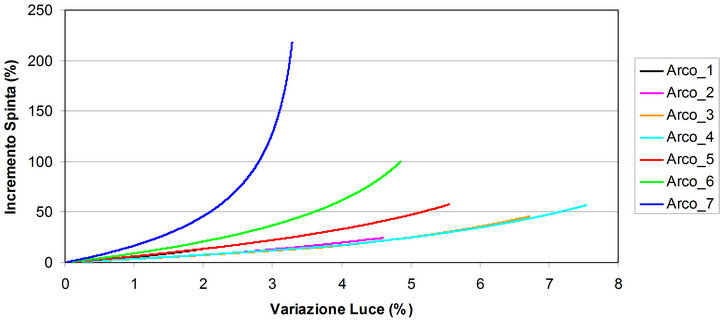
Figure 4. Summary graphs associated with the definition of the peak settlements of the right springing of a series of arches with changing springing angle and rise.
In the same figure two summary graphs, that interpret the non-linear aspect of the problem, are highlighted. The first graph shows the relationship between external settlement and vertical displacement of the centroid of one of the two keystone ashlars. The second curve shows, instead, the relationship between the percentage increase of the thrust, measured with respect to the initial one, and the percentage increase change of the spam due to the removal of the abutments because of the progressive assigned horizontal settlement.
Figure 5 refers to a comparison of two structures for which it is possible to see a substantial difference in the behaviour under the action of the horizontal settlement (applied in the same manner in both cases) at the base of the right pier.
The calculation procedure uses the hypothesis of the elastic-cracking joint. Geometry (where pier height = 300 cm and spam = 260 cm), self-weights and elastic characteristics of the joints describe, also in this case, a configuration sufficiently realistic.
The two peak settlements differ in a ratio of about 1:20, in the sense that the structure on the left, with the help of the masonry placed on the extrados of the arch, appears considerably more stable than the structure on the right (that, in the examined case, at most, tolerates a displacement of the base of the pier of about 2.7 cm). The con-
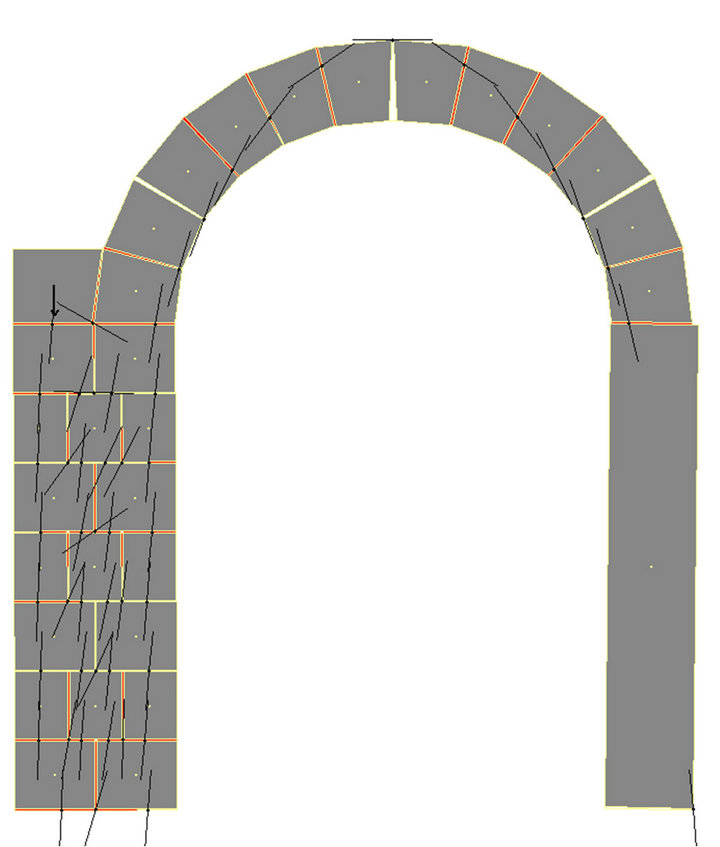

Figure 5. Arches settled on asymmetric piers and subjected to horizontal settlement of the base of the right pier.

Figure 6. Trabs in the Pompeianus Forum.

Figure 7. Trabs in the Pompeianus Forum. Vertical settlement of the right pier.
figuration shown in the figure highlights, in fact, the limit position of the line of thrust at the base of the right pier. The structure on the left collapses because of the total detachment of the portion of masonry placed on the right extrados of the arch, as a result of a deformed configuretion greatly compromised.
Finally, Figures 6 and 7 show the behaviour of a portion of the trabs in the Pompeianus Forum subjected to a vertical settlement of the first pier on the right [22]. The effectiveness of the masonry apparatus, composed of large stones in the long architrave, shows how its behaveiour is recognized as being similar to that of a Gerber beam.
The structure is able to respond effectively to a settlement of the pier higher than 25 cm showing, even if with a clear rotation of the blocks, an overall structural scheme still in equilibrium.
7. Conclusion
The numerical model presented here seems to be paticularly effective in finding the relationships between crack patterns and external settlements in the case of masonry structures formed by the assembly of elements according to different constructive typologies. For some cases, where it has been possible to make experimental investigations and build laboratory models, the correspondence between the behaviour of these models and the results obtained using the method described above can be considered almost perfect. All this suggests it is necessary to conduct a more in-depth research of the subject with the aim of refining, in particular, the kinematical analysis of the elements in which the geometric congruence of the contact points along the interfaces between the blocks is controlled in such a way as to avoid possible solutions in which penetration of material is present at the perimeters of the blocks themselves.
8. Acknowledgements
The authors wish to thank Libby Lee for her help with the review and revision of this article.
REFERENCES
- J. Heyman, “The Masonry Arch,” 1st Edition, Ellis Horwood Ltd., Chichester, 1982.
- M. Como, “Equilibrium and Collapse Analysis of Masonry Bodies,” Meccanica, Vol. 27, No. 3, 1992, pp. 185- 194. doi:10.1007/BF00430044
- M. Gilbert, C. Casapulla and H. M. Ahmed, “Limit Analysis of Masonry Block Structures with Non-Associative Frictional Joints Using Linear Programming,” Computers and Structures, Vol. 84, No. 13-14, 2006, pp. 873- 887. doi:10.1016/j.compstruc.2006.02.005
- J. Heyman, “La Coupe des Pierres,” Proceedings of the 3rd International Congress on Construction History, Cottbus, May 2009.
- M. Paradiso, G. Tempesta and S. Galassi, “A Numerical Method for No-Tension Analysis of Masonry Arches,” Proceedings of the 4th International Conference on Arch Bridges, Barcellona, 17-19 Novembre 2004, pp. 312-321.
- J. Ochsendorf, “The Masonry Arch on Spreading Supports,” The Structural Engineeer, Vol. 84, No. 2, 2006, pp. 29-36.
- C. Baggio and P. Trovalusci, “Collapse Behaviour of Three-Dimensional Brick-Block Systems Using Non-Linear Programming,” Structural Engineeering and Mechanics, Vol. 10, No. 2, 2000, pp. 181-195.
- S. Di Pasquale, “New Trends in the Analysis of Masonry Structures,” Meccanica, Vol. 27, No. 3, 1992, pp. 173- 184. doi:10.1007/978-94-017-2188-2_3
- C. A. Coulomb, “Mémoires de Mathématique et de Physique Présentés à l’Académie Royale des Sciences, par Divers Savans, et Ius dans les Assemblées,” Académie Royale des Sciences, Paris, 1776.
- M. Paradiso, G. Tempesta, S. Galassi and F. Pugi, “Sistemi Voltati in Muratura. Teoria e Applicazioni,” Edizioni DEI, Roma, 2007.
- S. Galassi, M. Paradiso and G. Tempesta, “X-Vaults: A Software for the Analysis of the Stability of Masonry Cross-Vaults,” Computer Science Issues, Vol. 9, No. 2, 2012, pp. 133-142.
- G. Colonnetti, “Scienza delle Costruzioni,” Edizioni Scientifiche Einaudi ,Torino, 1955.
- A. Ben Israel and T. N. E. Greville, “Generalized Inverses: Theory and Applications,” John Wiley & Sons, New York, 1974.
- M. Gilbert and C. Melbourne, “Rigid-Block Analysis of Masonry Structures,” The Structural Engineering, Vol. 72, No. 21, 1994, pp. 356-361.
- C. A. Castigliano, “Théorie de l’Équilibre des Systèmes Élastiques et ses Applications,” Editore Negro, Torino, 1879.
- J. Ochsendorf, “Collapse of Masonry Structures,” Ph.D. Dissertation, University of Cambridge, Cambridge, 2002.
- S. Galassi, M. Paradiso, E. Pieroni and G. Tempesta, “Analisi di Strutture in Muratura Soggette a Vincoli Cedevoli: Un Algoritmo di Calcolo Non Lineare,” Proceedings of XX Congresso Associazione Italiana di Meccanica Teorica e Applicata, AIMETA 2011, Publi& Stampa Edizioni, Bologna, 12-15 Settembre 2011.
- S. Galassi, M. Paradiso, E. Pieroni and G. Tempesta, “Analisi di Archi in Muratura su Imposte Cedevoli,” Atti del Workshop on Design for Rehabilitation of Masonry Structures WONDERmasonry 2011, Edizioni Polistampa, Firenze, Luglio 2012, pp. 48-58.
- V. Ceradini, M. Candela and R. Fonti, “The Role of Solid Springer in Masonry Vault,” Advanced Materials Research, Vol. 133-134, 2010, pp. 349-354. doi:10.4028/www.scientific.net/AMR.133-134.349
- S. Huerta, “Mechanics of Masonry Vaults: The Equilibrium Approach,” Proceedings of 3th International Seminar on Historical Constructions, Guimaraes, 2001, pp. 247-253.
- S. Galassi, “BrickWORK: A Software for the Analysis of Masonry Structures Composed of Rigid Blocks Jointed with or without Interposition of Mortar; A Tool Derived from the Scientific Research of the Authors, Not for Sale,” 2007-2012.
- S. Di Pasquale, “L’Arkh-Trabs del Foro Pompeiano,” Atti del Convegno Internazionale di Studi “Ercolano 1738- 1988-250 anni di Ricerca Archeologica, Roma, 20 Ottobre-5 Novembre 1988, pp. 201-218.

