Open Journal of Civil Engineering
Vol.3 No.2(2013), Article ID:32273,8 pages DOI:10.4236/ojce.2013.32009
Modelling and Analysis of Base Isolated Structures with Friction Pendulum System Considering near Fault Events
Department of Civil Engineering, University of Salerno, Salerno, Italy
Email: petti@unisa.it, fabriziopolichetti@email.it, alodato@unisa.it, palazzo@unisa.it
Copyright © 2013 Luigi Petti et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 21, 2013; revised March 22, 2013; accepted April 1, 2013
Keywords: Base Isolated Structures; Friction Pendulum Slide Bearings; Spatial Seismic Demand
ABSTRACT
The seismic behavior of base isolated structures with friction pendulum slide bearings devices subjected to near fault events characterized by significant vertical ground motion components is investigated. In particular, in order to evaluate the effects of vertical components on seismic response, non-linear dynamic analysis, carried out by using several numerical models, have been performed by considering two near-fault seismic events, L’Aquila 2009 and Emilia Romagna 2012. The obtained results show that increasing vertical seismic motion base shear significantly increases while relative displacements increase very little.
1. Introduction
In the last years, along with multilayer elastomeric bearings, more new isolator types, such as friction pendulum systems, have been developed taking advantage of a different approach like the friction systems. Within this, the friction pendulum slide bearings (FPBs) are rather widely applied nowadays leading to both affordability and very high fundamental periods. Moreover, characteristics of high rigidity to wind and minor earthquake loads, and high vertical load capacity and stability make FPBs suitable for many different situations.
The friction pendulum bearings consists of a spherical sliding surface which realize a pendulum system whose fundamental period is related essentially to the length of the pendulum, otherwise the radius of curvature of the spherical sliding surface. Observing that the dynamic response of the bearing is strictly related to the friction behavior, differently from elastomeric ones, the behavior of FPBs is affected by normal force and therefore vertical component of the ground motion could play a fundamental role.
Seismic codes, like the Italian NTC 2008, generally allow to use linear and/or non linear analysis by considering two main horizontal directions but no particular requirements for the vertical ground motion component are considered.
In this within, several studies can be found in literature for the case of multilayer elastomeric bearings. For the case of FPBs some research was done by Constantinou [1] showing that there is some interaction between the orthogonal components of the frictional force at the sliding interface.
Many numerical tests on a rigid frame model were conducted by Whittaker [2], showing that the effect of vertical shaking on the force and displacement response is negligible. In 2009, Khoshnoudian and Hagdoust [3] showed that the interaction between the stiffness of the two horizontal directions reduces structural shear and base shear, and that vertical component of an earthquake considerably affect lateral responses.
The study aim is to investigate two aspects of Friction Pendulum Bearings behavior: the influence of the vertical component of seismic motion in case of near-fault events; to analyze the seismic response of these systems subjected to tridimensional ground motions. For this purpose several non linear numerical models are comparatively considered to near fault events of L’Aquila 2009 and Emilia Romagna 2012 considering an ideal isolated system characterized by a perfect rigid superstructure neglecting lateral-torsional effects. In particular, the results obtained by SAP2000 [4], 3D models, are compared to the ones obtained in MATLAB [5], 2D models without considering vertical components. The results obtained in MATLAB are represented by using polar spectra [6,7].
Results have been carried out and compared with those obtained by using single component of the excitations by varying radius of curvature and friction of FPBs, examining the effect of vertical component on the base relative displacement, base shear and effective fundamental vibration period.
2. Principles of Friction Pendulum Bearings
The FPBs consists of a spherical sliding surface and an articulated slider which is faced with a high pressure capacity bearing material. The bearing, which realize a pendulum system, may be installed also upside-down with the spherical surface facing down rather than up. In both installation methods the behavior is identical. A cross section view of an FPBs is shown in the following Figure 1.
In particular, a friction pendulum system is constituted by a swivel slider that oscillates around the center of curvature of a concave spherical surface whose radius R is equivalent to the pendulum length (Figure 2).
One of the most important properties of FPB isolated systems is that the fundamental period of vibration 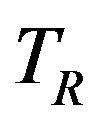 of the isolated system is independent of the overall mass [8] and can be evaluated by the pendulum behavior as:
of the isolated system is independent of the overall mass [8] and can be evaluated by the pendulum behavior as:
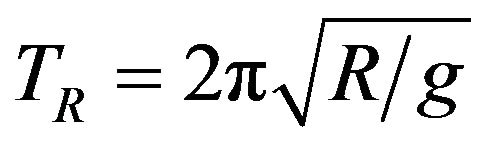 (1)
(1)
The lateral force provided by an FPBs is directly proportional to the weight W it carries and, thus, generally the isolation system force always develops at the center of mass of the supported structure if overturning effects and vertical behavior are neglected. For the single bearing, the friction force is equal to:
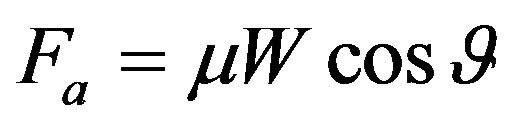 (2)
(2)
which leads, by considering the rotational equilibrium, to the following horizontal restoring force F:
 (3)
(3)
where  is the dynamic friction coefficient, D the horizontal displacement, W the vertical load and R the radius of the curvature of the bearing.
is the dynamic friction coefficient, D the horizontal displacement, W the vertical load and R the radius of the curvature of the bearing.
In the case of small oscillations, low values of the ratio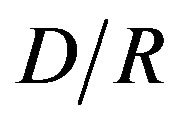 , the relationship between the restoration force and displacement (Figure 2) can be write as:
, the relationship between the restoration force and displacement (Figure 2) can be write as:
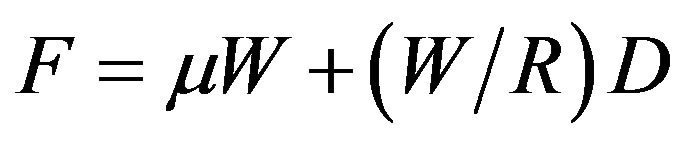 (4)
(4)
As Figure 2 shows, real FPB device presents initial elastic stiffness due to the constitutive material behavior. Instead, the secant stiffness can be evaluated in correspondence of the maximum displacement 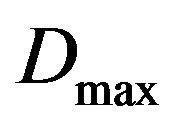 as:
as:
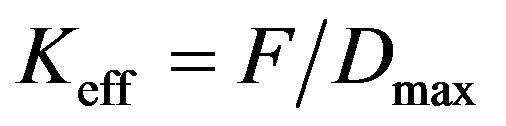 (5)
(5)
Therefore, the effective fundamental vibration period
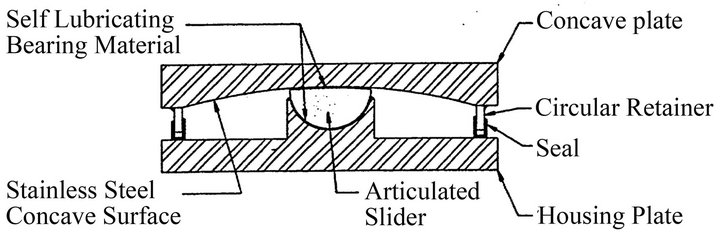
Figure 1. Friction pendulum system [9].
 (a)
(a)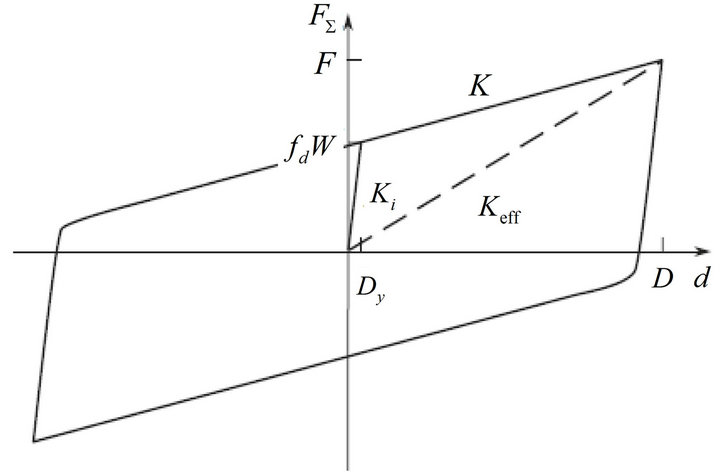 (b)
(b)
Figure 2. (a) Equilibrium of the pendulum; (b) Dynamical characteristics of an FPS.
 does not coincide with the reference period
does not coincide with the reference period 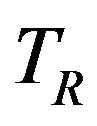 evaluated from pendulum behavior being:
evaluated from pendulum behavior being:
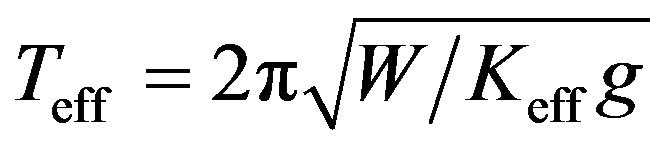 (6)
(6)
The effective damping provided by a friction isolator is equal to the integer of the hysteresis cycle area [10] :
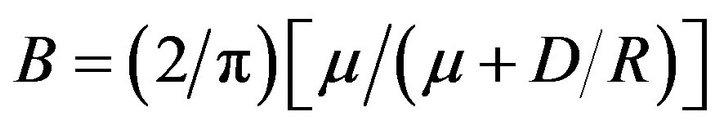 . (7)
. (7)
3. Considered Seismic Events
To evaluate the effects of the vertical ground motion components on the seismic behavior of isolated systems with FPBs the L’Aquila 2009 and Emilia Romagna 2012 near fault events have been considered. In the following, Magnitude and Peak Ground Acceleration (PGA) for horizontal (X and Y) and vertical (Z) components are represented in Table 1.
A plot of the acceleration spectra along the three main directions, for the two stations, is showed in the Figures 3 and 4:

Table 1. Considered events, seismic parameters.

Figure 3. Acceleration spectra (L’Aquila event).
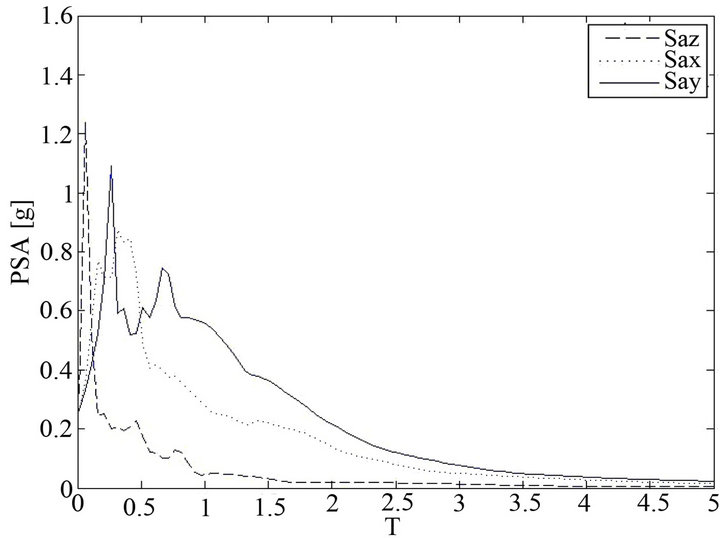
Figure 4. Acceleration spectra (Emilia Romagna event).
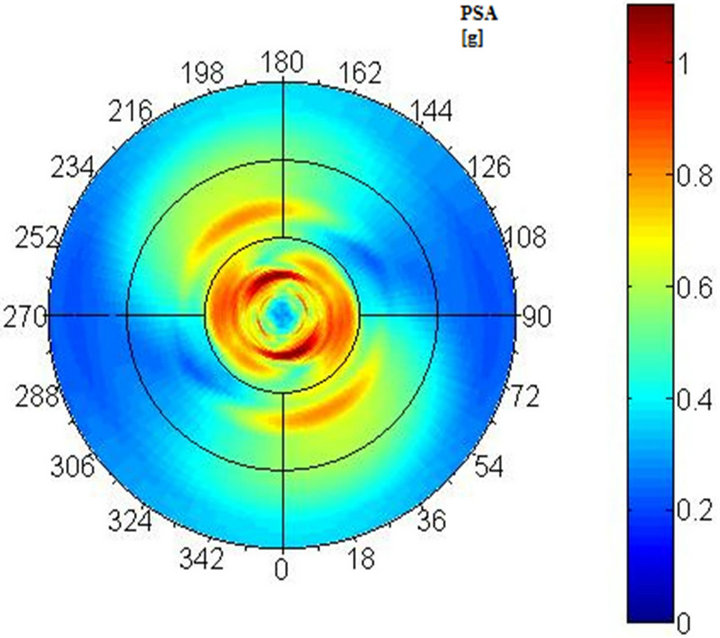
The considered seismic events are characterized, as shown in [6,7], by strong local directivity effects. In the following, polar spectrum in terms of pseudo-acceleration (PSA) and displacement (SD) are represented in the Figures 5 and 6 for both the case. In particular, the plots represent the seismic spectra demand in each horizontal direction by means of graduated color maps. In correspondence to each radius the in-plan projection of the spectrum response evaluated along that direction is represented. Instead, in correspondence to each circumference the spectral demand for a fixed period is plotted for each direction being considered. In the represented Polar Spectra, the periods 0.5, 1.0 and 1.5 are marked by thin black circumferences and the origin corresponds to 0 sec period.
 (a)
(a)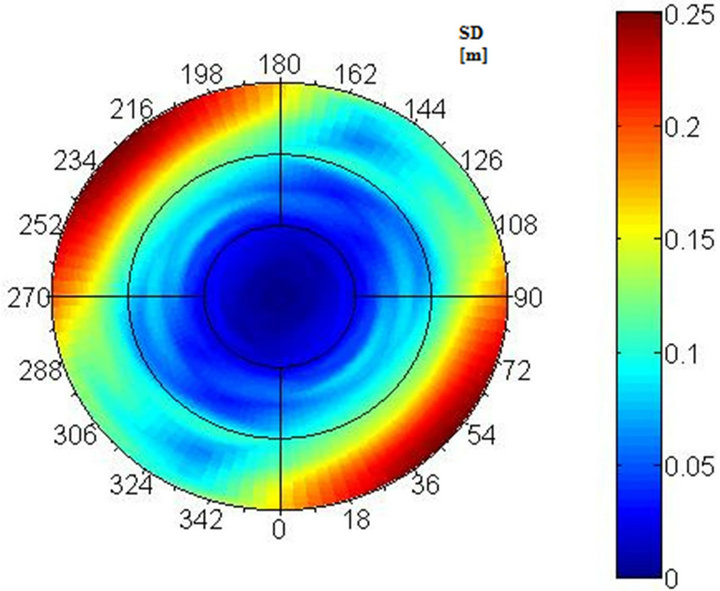 (b)
(b)
Figure 5. Polar spectrum for AQK station in terms of: (a) Pseudo-accelerations; and (b) Displacements [6].
 (a)
(a)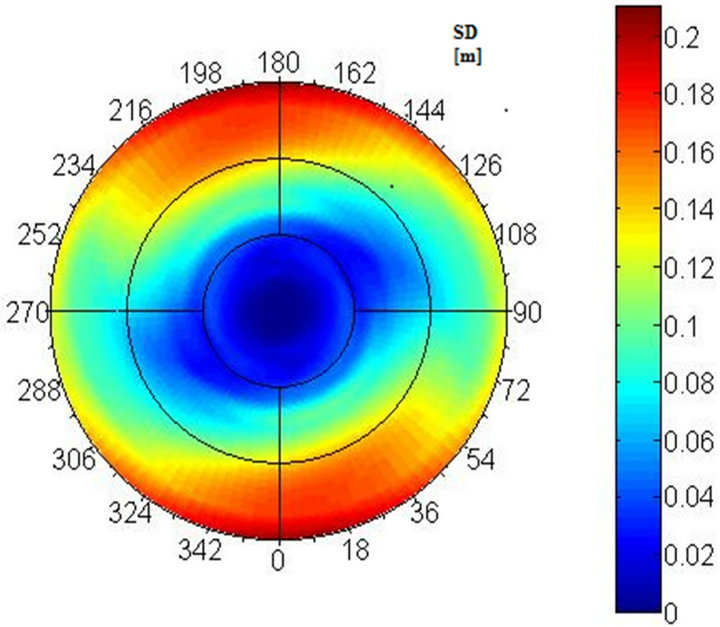 (b)
(b)
Figure 6. Polar spectrum for MRN station in terms of: (a) Pseudo-accelerations; and (b) Displacements [7].
Polar Spectra show that for the AQK station the maximum spectral demands generally are reached in the NW-SE direction for periods around 1.5 sec and 0.2 - 0.7sec respectively for SD and PSA demands. In the case of MRN station the maximum response generally is attained in the NNW-SSE direction for periods around 1,5 sec for SD and 0.3 and 0.7 sec for PSA demands. Moreover PSA presents high values around 0.45 sec in the EW direction.
4. Mathematical Models
Two models are considered in the paper to evaluate the response of base isolated system. The first one is carried out by Matlab procedures and consists of a SDOF system with friction layer representing the FPBs. The equation of motion of the considered system, neglecting the vertical component of motion, is expressed as:
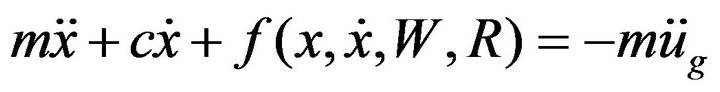 (8)
(8)
where m, c, x and 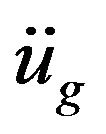 respectively represents the overall mass of the isolated system, the damping coefficient, the relative displacement and the ground displacement. The equation of motion could be writing, by dividing by mass, also as:
respectively represents the overall mass of the isolated system, the damping coefficient, the relative displacement and the ground displacement. The equation of motion could be writing, by dividing by mass, also as:
 (9)
(9)
where  represents the damping factor. For the research purpose, analyses have been carried out with and without considering the terms
represents the damping factor. For the research purpose, analyses have been carried out with and without considering the terms  which represents the hardening effects in the model due to the uplift of the mass in the pendulum model.
which represents the hardening effects in the model due to the uplift of the mass in the pendulum model.
The second model is represented by a 3-DOF system described in SAP 2000. For the purpose of the research the overall system is described by a concentrated mass with no rotational degree of freedom. The model uses a biaxial friction pendulum isolator (Figure 7) that leads to coupled friction properties for the two horizontal shear deformations, post slip stiffness in the shear directions due to the pendulum radii and gap behavior in the axial direction. The friction forces are directly proportional to the compressive axial force and the element cannot carry axial tension.
The friction model is based on the hysteretic behavior proposed by Wen and Park [11], Wen and Ang [12], and recommended for base isolation analysis by Nagarajaiah, Reinhorn and Constantinou [13].
The results obtained from the two different models are comparatively analyzed in the following to validate the results and underline the application limits of the sliding systems with regard to seismic motions for which the vertical component play a fundamental rule in the building design.
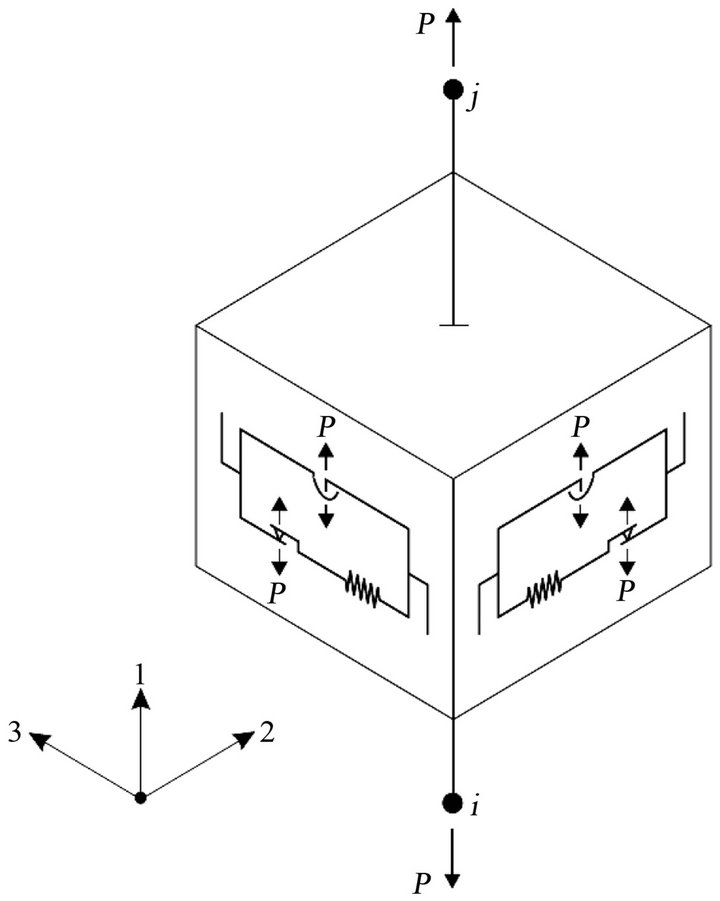
Figure 7. Friction pendulum isolator property [4].
5. Non-Linear Analysis
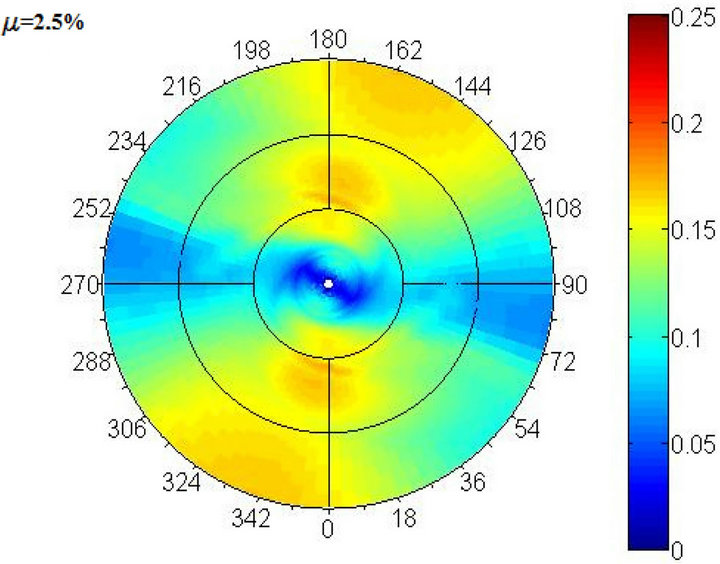
A wide set of non linear dynamic analysis has been carried out to analyze seismic response of isolated systems by means of FPBs. In the following, to preliminary characterize the system behavior, the response in terms of spectral displacements by considering the 2D numerical model in MATLAB is plotted by using polar representation [6,7]. In particular, spectra of displacement evaluated in the periods range 0 - 5 sec are obtained by changing FPB radius according to the pendulum formulation. Results for the AQK and MRN stations are represented in the Figures 8 and 9 by neglecting the vertical ground motion component.
Results first of all show that in the case of hardening behavior the maximum displacement response is attained in the NW-SE direction for periods range 1.5 - 4 sec in the case of AQK station and in the NE-SW direction for periods range 1.5 to 5 sec in the case of MRN. Instead, for the case without hardening behavior the maximum response, attained in the same directions, seems to be independent from the periods.
To investigate the effects on the seismic behavior of the vertical ground motion components several non-linear dynamic analysis have been carried out by SAP 2000 model by considering for FPBs three radii R (1, 2 and 4 m) and three friction coefficients μ (0.025, 0.05 and 0.10). The Figures 10-17 describe the results obtained alternatively for AQK and MRN stations with (3-D) and without (2-D) vertical ground motion components.
In particular, Figures 10 and 11 represent the maximum relative displacements dmax, Figures 12 and 13 the ratios between the maximum base shear Smax and the overall weight of systems W, Figures 14 and 15 the ra-
 (a)
(a)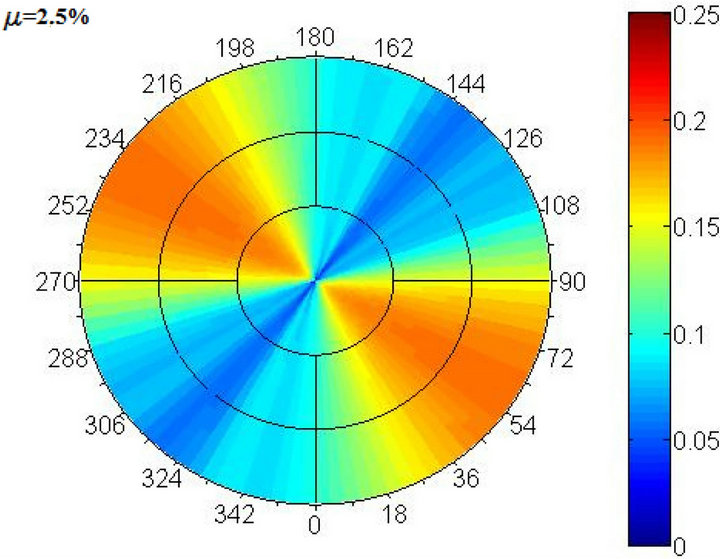 (b)
(b)
Figure 8. Non-linear polar spectrum of displacement with (a) and without (b) hardening effects, AQK station.
tios between the maximum absolute accelerations aabs and g and Figures 16 and 17 the ratios between the effective vibration periods  and the reference ones Tr.
and the reference ones Tr.
Analysis of results show that the seismic behavior of the isolated systems with FPBs is generally considerably affected by the vertical ground motion components. In particular base shear and absolute acceleration increase for considered events up to the double for the case of MRN station. Instead, the maximum relative displacements generally increase less and, finally, no remarkable differences are found on effective periods. Usually, the response worsen by decreasing the radii of FPBs. Moreover, the case with radius equal to 1 m presents a trend inversion with regard to the higher considered radii. Finally, the effective vibration periods decrease slightly by increasing the friction coefficient and the radii of FPBs.
To better investigate the effects of vertical ground motion components, the Figures 1-25 describe the seismic response by varying the PGA of vertical components scaling the original records for AQK and MRN stations. In particular, Figures 18-21 describes the ratios between the maximum relative displacements dmax obtained with (3D) and without (2D) the vertical ground motion in the case of 0.025 and 0.10 friction coefficients. The Figures 22-25 represent instead the ratios between the base shear
 (a)
(a) (b)
(b)
Figure 9. Non-linear polar spectrum of displacement with (a) and without (b) hardening effects, MRN station.
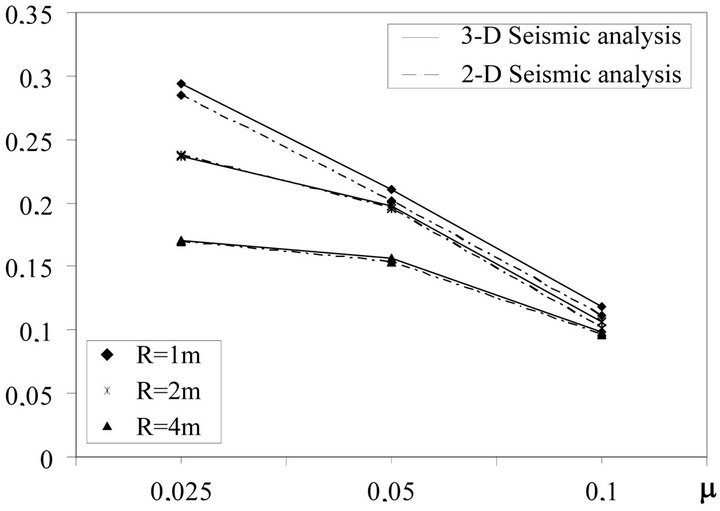
Figure 10. Maximum displacement dmax (m), AQK site.
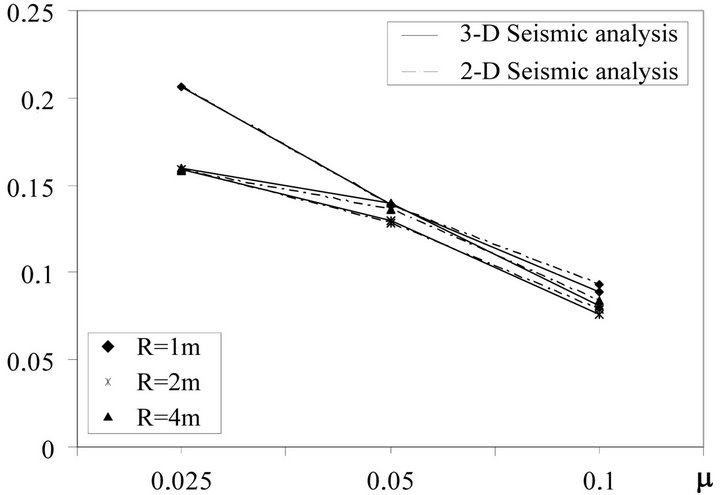
Figure 11. Maximum displacement dmax (m), MRN site.

Figure 12. Ratio Smax/W, AQK site.
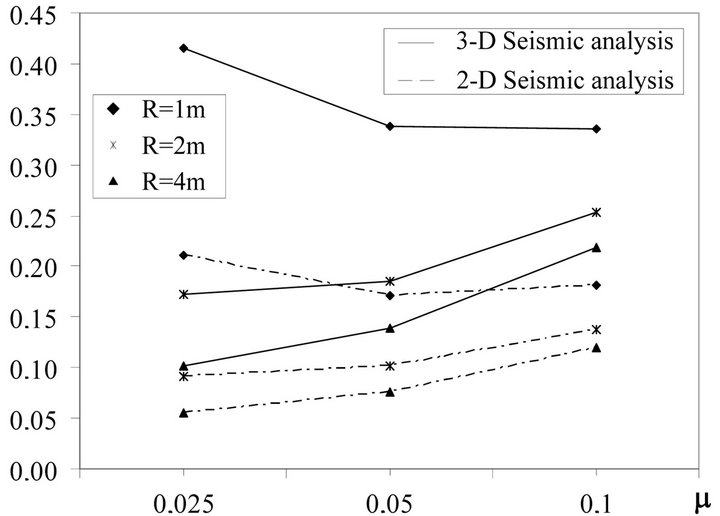
Figure 13. Ratio Smax/W, MRN site.
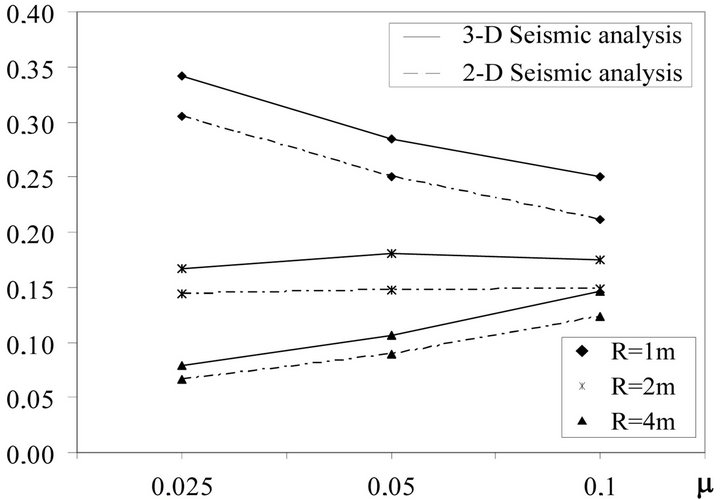
Figure 14. Ratio aabs/g, AQK site.

Figure 15. Ratio aabs/g, MRN site.

Figure 16. Ratio Teff /Tr, AQK site.
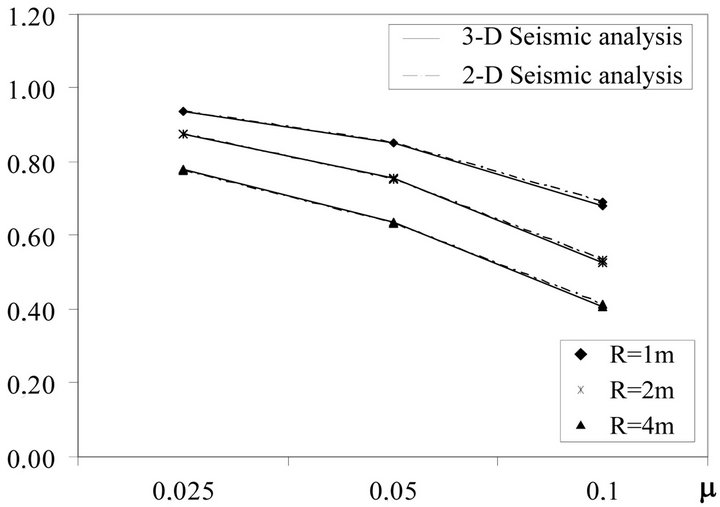
Figure 17. Ratio Teff /Tr, MRN site.
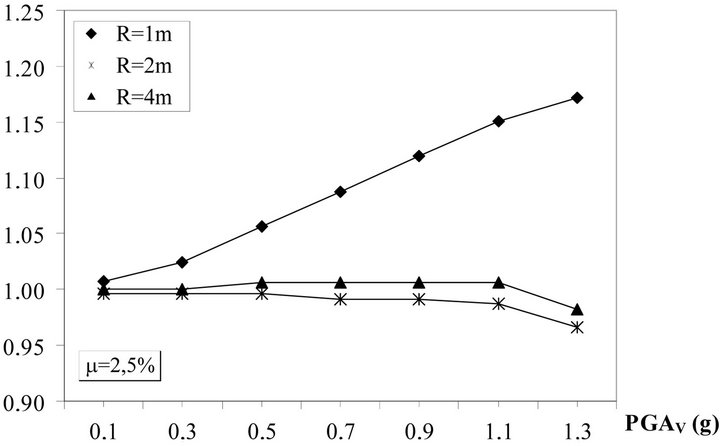
Figure 18. Ratio dmax (3D)/dmax (2D), AQK site.

Figure 19. Ratio dmax (3D)/dmax (2D), MRN site.

Figure 20. Ratio dmax (3D)/dmax (2D), AQK site.

Figure 21. Ratio dmax (3D)/dmax (2D), MRN site.
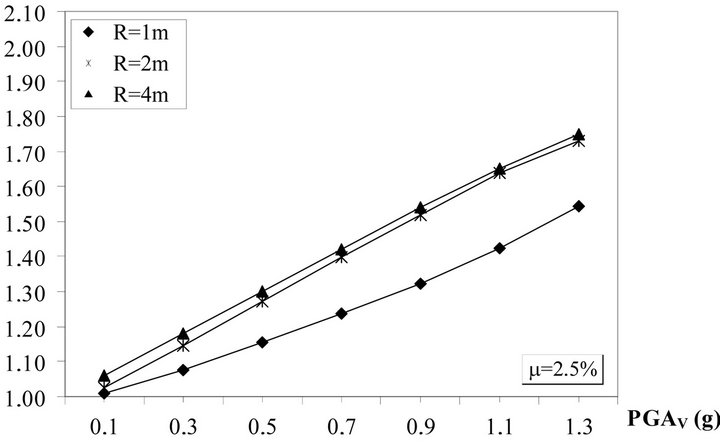
Figure 22. Ratio Smax (3D)/Smax (2D), AQK site.
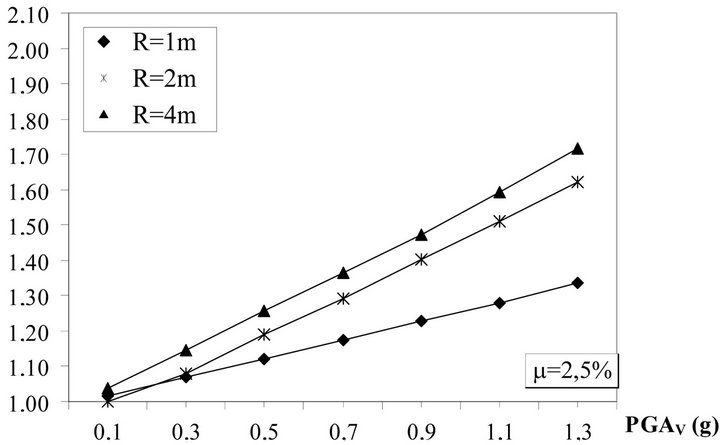
Figure 23. Ratio Smax (3D)/Smax (2D), MRN site.

Figure 24. Ratio Smax (3D)/Smax (2D), AQK site.
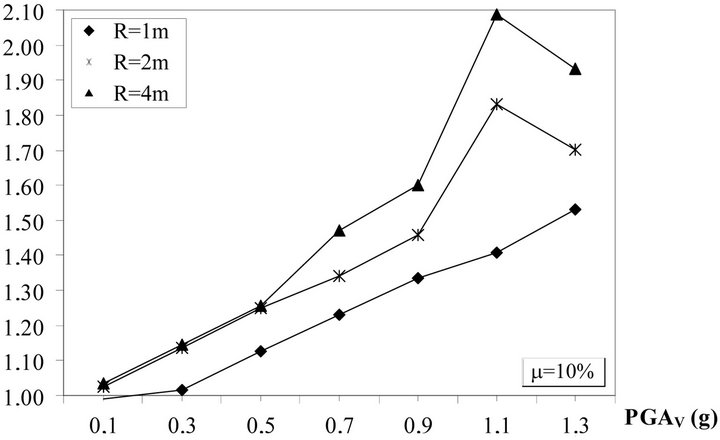
Figure 25. Ratio Smax (3D)/Smax (2D), MRN site.
evaluated with (3D) and without (2D) the vertical ground motion for the same cases.
The analysis of results show that in the case of 0.025 friction coefficient, with exception of radius equal to 1m, there are no practically increase of the relative displacements, while the base shear ratio increase linearly with vertical PGA up to 1.75 in correspondence of PGA equal to 1.3 g.
In the case of 0.10 friction coefficient the displacement ratio reaches 1.25 for the radius equal to 1m and the base shear ratio increases up to 2.10 in correspondence of PGA equal to 1.1 g.
6. Conclusive Remarks
The effects of taking into account vertical seismic component on the overall behavior of isolated structures with FPBs in case of near fault events, is investigated in this paper.
In particular, to investigate the potential performance that could be achieved by FPBs, the study considered an ideal isolated system characterized by a perfect rigid superstructure neglecting lateral-torsional effects. To assess the seismic response to near fault events, like L’Aquila 2009 and Emilia Romagna 2012, a non-linear 3-DOF system was implemented in SAP 2000. Moreover, nonlinear polar spectra responses were obtained by means of MATLAB neglecting the vertical component of seismic motion.
The obtained results by 2D model in MATLAB validate the ones carried out with the 3D model in SAP2000. Results generally show a great relevance of the vertical ground motion, most of which on the base shear, with a linear increase of the response up to the double of the case without vertical seismic component when PGAV reaches 1 g. Instead, the relative displacements substantially are not highly influenced by the vertical ground motion with exception for small radius of curvature, where the increment reaches the 20% when PGAV reaches 1 g.
REFERENCES
- A. S. Mokha, M. C. Constantinou and A. M. Reinhorn, “Verification of Friction Model of Teflon Bearings under Triaxial Load,” Journal of Structural Engineering, Vol. 119, No. 1, 1993, pp. 240-261.
- G. Mosqueda, A. S. Whittaker and G. L. Fenves, “Characterization and Modeling of Friction Pendulum Bearings Subjected to Multiple Components of Excitation,” Journal of Structural Engineering, Vol. 130, No. 3, 2004, pp. 433-442. doi:10.1061/(ASCE)0733-9445(2004)130:3(433)
- F. Khoshnoudian and V. Rezai Hagdoust, “Response of Pure-Friction Sliding Structures to Three Components of Earthquake Excitation Considering Variations in the Coefficient of Friction,” Civil Engineering, Vol. 16, No. 6, 2009, pp. 429-442,
- CSI Analysis Reference Manual, “SAP 2000,” Berkeley.
- MATLAB, “The Language of Technical Computing,” The Mathworks.
- L. Petti and A. Lodato, “Preliminary Spatial Analysis and Comparison between Response Spectra Evaluated for Emilia Romagna Earthquakes and Elastic Demand Spectra According to the New Seismic Italian Code,” Report ReLuis, 2012.
- L. Petti and I. Marino, “Preliminary Comparison between Response Spectra Evaluated at Close Source for L’aquila Earthquake and Elastic Demand Spectra According to the New Seismic Italian Code,” Report ReLuis, 2009.
- O. Soon-Taek and S. K. Young, “Experimental and Analytical Investigation of a Seismically Isolated Bridge Model with Friction Pendulum System,” KSCE Journal of Civil Engineering, Vol. 2, No. 3, 1998, pp. 265-272.
- Nistir 5800, “Guidelines for Pre-qualification, Prototype and Quality Control Testing of Seismic Isolation System,” 1996, 143 p.
- V. A. Nadein, Yu. N. Drozdov, V. N. Puchkov and M. V. Puchkov, “Characteristics of Pendulum Sliding Bearings Used as Seismic Isolators,” Russian Engineering Research, Vol. 27, No. 2, 2007, pp. 85-92.
- Y. K. Wen, “Method for Random Vibration of Hysteretic Systems,” Journal of the Engineering Mechanics Division, Vol. 102, No. 2, 1976, pp. 249-263.
- Y. J. Park, Y. K. Wen and A. H.-S. Ang, “Random Vibration of Hysteretic Systems under Bi-Directional Ground Motions,” Earthquake Engineering and Structural Dynamics, Vol. 14, No. 4, 1986, pp. 543-557.
- S. Nagarajaiah, A. M. Reinhorn and M. C. Constantinou, “3D-Basis: Non-Linear Dynamic Analysis of Three-Dimensional Base Isolated Structures: Part II,” Technical Report NCEER-91-0005, National Center for Earthquake Engineering Research, State University of New York at Buffalo, Buffalo, 1991.

