Open Journal of Civil Engineering
Vol.2 No.3(2012), Article ID:22980,11 pages DOI:10.4236/ojce.2012.23016
Simulation and Modelling of Smart Beams with Robust Control Subjected to Wind Induced Vibration
1Department of Civil Engineering, Technological Educational Institute of Crete, Crete, Greece
2Department of Production Engineering and Management, Technical University of Crete, Crete, Greece
Email: amalia@staff.teicrete.gr, gestavr@dpem.tuc.gr, tasos@dpem.tuc.gr
Received May 22, 2012; revised June 28, 2012; accepted July 9, 2012
Keywords: Smart Structures; Finite Element Formulation; Uncertainty; Robust Performance; Reduced Order Control
ABSTRACT
This paper presents some recent developments in modelling and numerical analysis of piezoelectric systems and controlled smart structures based on a finite element formulation with embedded control. The control aims at vibration suppression of the structure subjected to external disturbances, like wind and noise, under the presence of model inaccuracies, using the available measurements and controls. A smart structure under dynamic loads is analysed and comparison between results for beam with and without control is made. The numerical results show that the control strategy is very effective and suppresses the vibrations of the structure.
1. Introduction
The intelligent material sector has broadly motivated research interest during the last decades. Materials are classified as intelligent if they exhibit the ability to sense a certain stimulus and initiate a reaction to it in a controlled manner [1-11]. An intelligent structure is a structural system or member with embedded sensors and actuators, combined with a control system that automates the structure's reaction to external loadings acting on it, by attenuating their influence or improving desirable responses. Development in this scientific discipline is aided by advances in material science as well as in the field of control. Material science research has spurred the development of new materials that can be incorporated in structures to be used as actuators and sensors [9-11].
In this paper, we address the problem of vibrations of intelligent structures. Stimuli may come from external perturbations of the system, disturbances or excitation that may cause structural vibrations, such as wind loading or earthquakes. An intelligent structure is expected to be able to sense the vibration and counteract it in a controlled fashion, so that vibration of the system be reduced and contained. To that end, a number of intelligent materials may be used as actuators and sensors. [9-11] Piezoelectric materials, memory materials, electrostrictive and magnetostrictive materials are such materials. In this work, we focus on the use of piezoelectric materials, given that they exhibit good sensing and actuation properties.
Among the commonly used optimal control schemes are LQR, and . It is known that if the controller is not robust enough, the uncertainties of the system may destroy the efficiency of the controller. The
. It is known that if the controller is not robust enough, the uncertainties of the system may destroy the efficiency of the controller. The , control provides better robustness than LQR [12-14]. The aim of this work is to design an
, control provides better robustness than LQR [12-14]. The aim of this work is to design an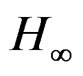 , robust controller for a beam bonded with piezoelectric sensors and actuators and to investigate the behaviour of the controlled beam. First, a detailed shear-deformable (Timoshenko) model for a laminated beam structure is developed. A finite element formulation is presented for the model. Quadratic Hermitian polynomials are used for the transverse and rotational displacements, respectively. The differential equations are based on the Timoshenko beam theory [15]. The governing state equation is established and used for the design of the control. The numerical simulations carried out on the laminated beam shows that the vibration of the system is significantly suppressed within the permitted actuator voltages. Herein the integration of control into a home-made finite element code developed in MATLAB is presented [16]. The numerical solution of the
, robust controller for a beam bonded with piezoelectric sensors and actuators and to investigate the behaviour of the controlled beam. First, a detailed shear-deformable (Timoshenko) model for a laminated beam structure is developed. A finite element formulation is presented for the model. Quadratic Hermitian polynomials are used for the transverse and rotational displacements, respectively. The differential equations are based on the Timoshenko beam theory [15]. The governing state equation is established and used for the design of the control. The numerical simulations carried out on the laminated beam shows that the vibration of the system is significantly suppressed within the permitted actuator voltages. Herein the integration of control into a home-made finite element code developed in MATLAB is presented [16]. The numerical solution of the  feedback controller has been done by using a nonconvex, non differentiable optimization approach with the usage of HIFOO software within MATLAB [14,17]. For the numerical results wind type loads are taken into account. The effectiveness of the technique in the modelling of the standard uncertainties is also presented.
feedback controller has been done by using a nonconvex, non differentiable optimization approach with the usage of HIFOO software within MATLAB [14,17]. For the numerical results wind type loads are taken into account. The effectiveness of the technique in the modelling of the standard uncertainties is also presented.
2. Mathematical Modelling
A cantilever slender beam with rectangular cross-sections is considered. Four pairs of piezoelectric patches are embedded symmetrically at the top and the bottom surfaces of the beam, as shown in Figure 1. The beam is made from graphite-epoxy T300-976 and the piezoelectric patches are PZT G1195N. The top patches act like sensors and the bottom like actuators. The resulting composite beam is modelled by means of the classical laminated technical theory of bending. Let us assume that the mechanical properties of both the piezoelectric material and the host beam are independent in time. The thermal effects are considered to be negligible as well [5, 6].
The beam has length L, width W and thickness h. The sensors and the actuators have width bS and bA and thickness hS and hA, respectively. The electromechanical parameters of the beam are given in the Table 1.
2.1. Reduced Piezoelectric Equations
In order to derive the basic equations for piezoelectric sensors and actuators (S/As), we assume that:
• The piezoelectric S/A are bonded perfectly on the host beam;

Figure 1. Beam with piezoelectric sensors/actuators.

Table 1. Parameters of the composite beam.
• The piezoelectric layers are much thinner then the host beam;
• The piezoelectric material is homogeneous, transversely isotropic and linearly elastic;
• The piezoelectric S/A are transversely polarized (in the z-direction) [5].
Under these assumptions the three-dimensional linear constitutive equations are given by [4],
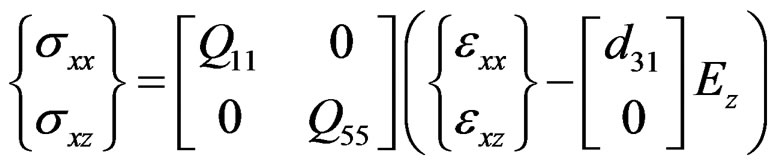 (1)
(1)
 (2)
(2)
where ,
,  denote the axial and shear stress components,
denote the axial and shear stress components, 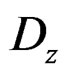 , denotes the transverse electrical displacement;
, denotes the transverse electrical displacement; 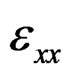 and
and 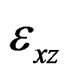 are a axial and shear strain components; Q11, and Q55, denote elastic constants; d31, and ξ33, denote piezoelectric and dielectric constants, respectively. Equation (1) describes the inverse piezoelectric effect and Equation (2) describes the direct piezoelectric effect. Ez, is the transverse component of the electric field that is assumed to be constant for the piezoelectric layers and its components in xy-plain are supposed to vanish. If no electric field is applied in the sensor layer, the direct piezoelectric Equation (2) gets the form,
are a axial and shear strain components; Q11, and Q55, denote elastic constants; d31, and ξ33, denote piezoelectric and dielectric constants, respectively. Equation (1) describes the inverse piezoelectric effect and Equation (2) describes the direct piezoelectric effect. Ez, is the transverse component of the electric field that is assumed to be constant for the piezoelectric layers and its components in xy-plain are supposed to vanish. If no electric field is applied in the sensor layer, the direct piezoelectric Equation (2) gets the form,
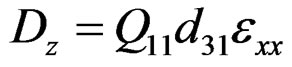 (3)
(3)
and it is used to calculate the output charge created by the strains in the beam [3].
2.2. Equations of Motion
The length, width and thickness of the host beam are denoted by L, b and h, respectively. The thickness of the sensor and actuator is denoted by hs and ha. We assume that:
• The beam centroidal and elastic axis coincides with the x-coordinate axis so that no bending-torsion coupling appears;
• The axial vibration of the host beam centreline is considered negligible;
• The displacement field {u} = (ux, uy, uz) is obtained based on the usual Timoshenko assumptions,
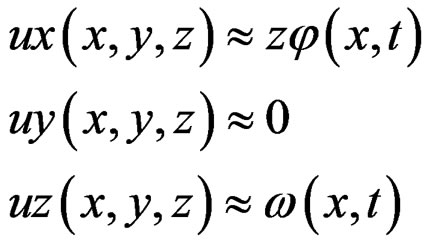 (4)
(4)
where φ is the rotation of the beams cross-section about the positive y-axis and w is the transverse displacement of a point of the centroidal axis (y = z = 0).
The strain displacement relations can be applied to Equation (4) to give,
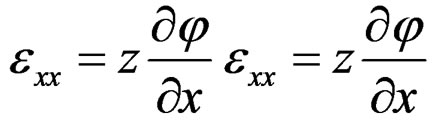 (5)
(5)
We suppose that the transverse shear deformation is equal to zero [2]. In order to derive the equations of the motion of the beam we use Hamilton’s principle,
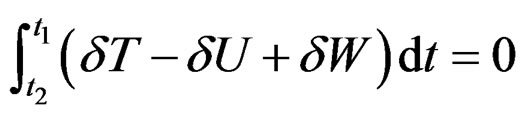 (6)
(6)
where T [6] is the total kinetic energy of the system, U is the potential (strain) energy and W is the virtual work done by the external mechanical and electrical loads and moments. The first variation of the kinetic energy is given by,
 (7)
(7)
The first variation of the kinetic energy is given by,
 (8)
(8)
If the load consists only of moments induced by piezoelectric actuators and since the structure has no bending twisting couple then the first variation of the work has the form [6],
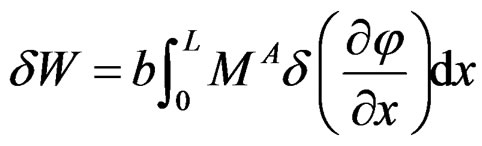 (9)
(9)
where MA is the moment per unit length induced by the actuator layer and is given by,
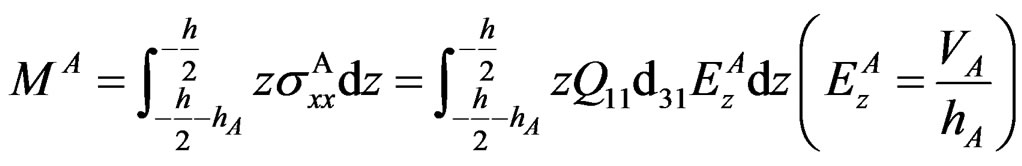 (10)
(10)
2.3. Finite Element Formulation
We consider a beam element of length Le, which has two mechanical degrees of freedom at each node: one translational ω1 (respectively ω2) in direction z and one rotational φ1 (respectively φ2), as it is shown in Figure 2. The vector of nodal displacements and rotations qe is defined as [3],
 (11)
(11)
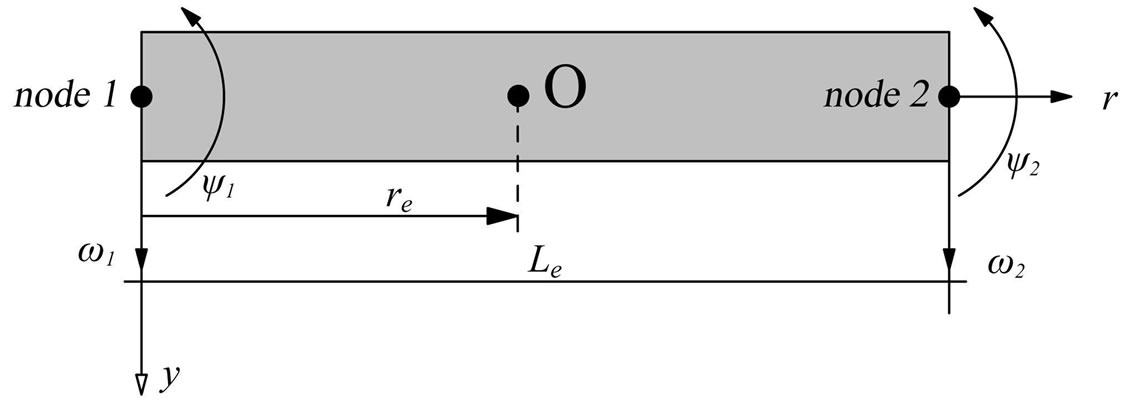
Figure 2. Beam finite element.
The beam element transverse deflection ω(x, t) and the beam element rotation ψ(x, t) of the beam are continuous and they are interpolated within by Hermitian linear shape functions  and
and  as follows [4],
as follows [4],
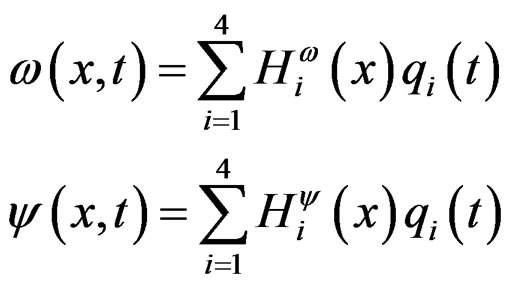 (12)
(12)
This classical finite element procedure leads to the approximate (discretized) variation problem. For a finite element the discrete differential equations are obtained by substituting the discretized expressions 12 into Equations (7) and (8) to evaluate the kinetic and strain energies. Integrating over spatial domains and using the Hamiltons principle 6 the equation of motion for a beam element are expressed in terms of nodal variable q as follows,
 (13)
(13)
where M is the generalized mass matrix, D the viscous damping matrix, K the generalized stiffness matrix, 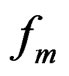 the external loading vector and
the external loading vector and 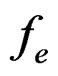 the generalized control force vector produced by electromechanical coupling effects. The independent variable q(t) is composed of transversal deflections
the generalized control force vector produced by electromechanical coupling effects. The independent variable q(t) is composed of transversal deflections 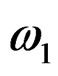 and rotations
and rotations , i.e., [7]
, i.e., [7]
 (14)
(14)
where n is the number of nodes used in analysis. Vectors ω and  are positive upwards. To transform to statespace control representation, let (in the usual manner),
are positive upwards. To transform to statespace control representation, let (in the usual manner),
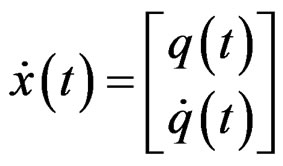 (15)
(15)
Furthermore to express  as
as  we write it as
we write it as 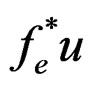 where
where  the piezoelectric force is for a unit applied on the corresponding actuator, and u represents the voltages on the actuators. Furthermore,
the piezoelectric force is for a unit applied on the corresponding actuator, and u represents the voltages on the actuators. Furthermore, 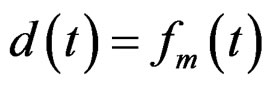 is the disturbance vector [18].
is the disturbance vector [18].
Then,
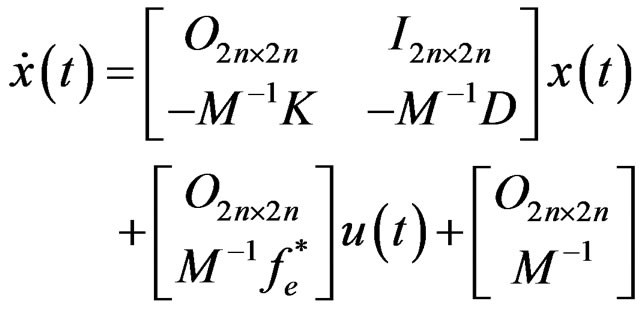 (16)
(16)
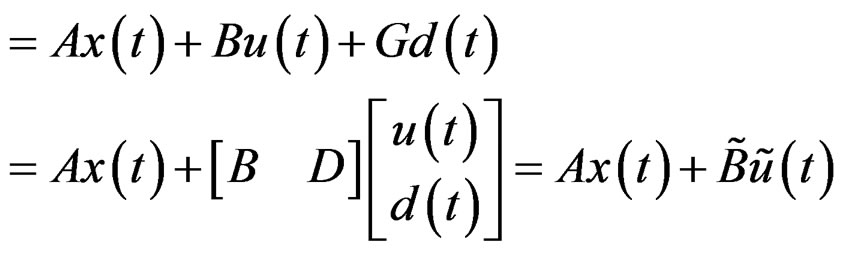 (17)
(17)
The previous description of the dynamical system will be augmented with the output equation (some displacements or velocities are measured) [4],
 (18)
(18)
In this formulation u is n × 1 (at most, but can be smaller), while d is 2n × 1. The units used are compatible for instance m, rad, sec and N.
3. Statement of the Robust Control Problem
The optimal control problem is initially studied for the nominal system, i.e., the beam with known elastic, piezoelectric and viscous properties. A more realistic question concerning the robustness of the control in the presence of defects is also addressed. The fact that the system is in subjected to disturbances, such as the wind power, as well as the noise of measurements, is taken into account. The mathematical pattern being used in the design is an approximation of the real one. Further, two control laws for the composite beam are designed in order to suppress the vibrations. Because of its linearity and easy implementation, the linear quadratic regulator (LQR) [13] is presented first. The response of the controlled nominal and damaged beams is investigated. In order to take into account the incompleteness of the information about the eventual damages and external additional influences a robust  controller is designed [12,14]. A system analysis is made on condition that the system is not accurate but includes uncertainty that may be related to some kind of damage [7].
controller is designed [12,14]. A system analysis is made on condition that the system is not accurate but includes uncertainty that may be related to some kind of damage [7].
For practical applications both algorithms need several trial-and-error design iterations in order to provide appropriate control voltages, since the piezoelectric actuators can be depolled by high oscillating voltages. The effectiveness of the proposed control strategies is investigated with the help of numerical simulations [3].
3.1. Robustness Analysis
The following three steps are taken in the robustness analysis [13,14,19]:
1) Expression of an uncertainty set by a mathematical model.
2) Robust stability (RS): check if the system remains stable for all plants within the uncertainty set.
3) Robust performance (RP): if the system is robustly stable, check whether performance specifications are met for all plants within the uncertainty set.
To perform the robustness analysis, the interconnection of Figures 3(a), (b) will be used.
Δ define the uncertainty, Μ define the nominal system, w are the inputs (the mechanical force and the noise of the system), z are the outputs (the state vector and the control vector). The uncertainty included in Δ
 (a) (b)
(a) (b)
Figure 3. Uncertainty modelling.
satisfies . Since controller K is known. Figure 3(a) can be simplified to Figure 3(b). Given this structure it is known that [16,19]1) The system (M, Δ) is robustly stable if,
. Since controller K is known. Figure 3(a) can be simplified to Figure 3(b). Given this structure it is known that [16,19]1) The system (M, Δ) is robustly stable if,
 (19)
(19)
where,
 (20)
(20)
is the structure singular value of M given the structured uncertainty set .
.
2) The system (M, Δ) exhibits robust performance if,
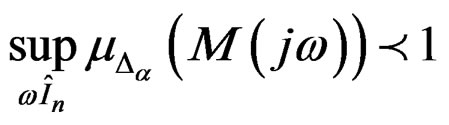 (21)
(21)
where,
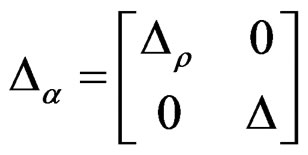
and  has the same structure as Δ but dimensions corresponding to (w,z). Unfortunately, only bounds on μ can be estimated.
has the same structure as Δ but dimensions corresponding to (w,z). Unfortunately, only bounds on μ can be estimated.
To proceed let us assume uncertainty in the M, D and K matrices of the form,
 (23)
(23)
with,
 (24)
(24)
This means that we are allowing a percentage deviation from the nominal values [4]. With these definitions Equation (13) becomes,
 (25)
(25)
where,
 (26)
(26)
Writing (25) in state space form, gives,
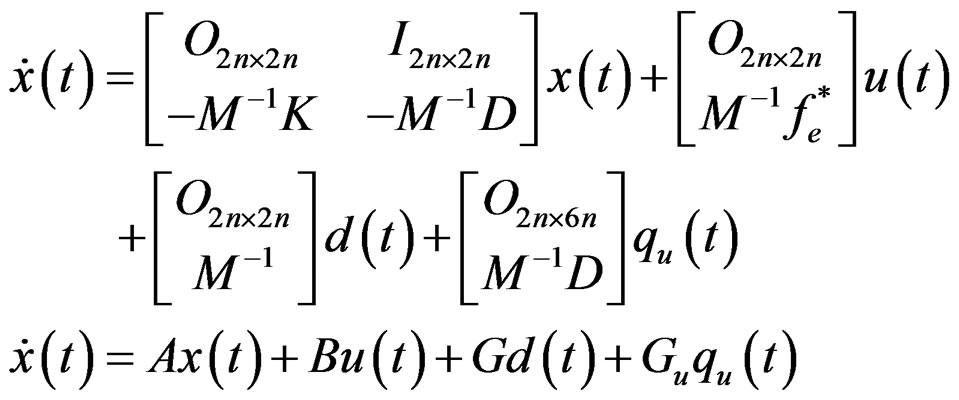 (27)
(27)
In this way we treat uncertainty in the original matrices as an extra uncertainty term.
4. Numerical Examples
For the numerical simulations a cantilever composite beam with viscous and piezoelectric layers bonded on its top and bottom and discretized with four finite elements, is used. A finer finite element discretization, which certainly is required for the approximation of higher frequencies, does not change the trend of the results. Our aim is to study the response of the composite beam in the presence of defects and damages.
Two kinds of dynamic loading are used as disturbances:
• Periodic sinusoidal loading pressure acting on the side of the structure simulating a strong wind. A sinusoidal load with an amplitude of 10 N and frequency of 6.2832 rad/sec, has been considered.
• A typical stochastic wind-type load on the side of the structure (Figure 4).
4.1. Results
The first load analyzed is sinusoidal load acting on the side of the structure. Figure 5 shows the dynamical response for the displacements of the uncontrolled and
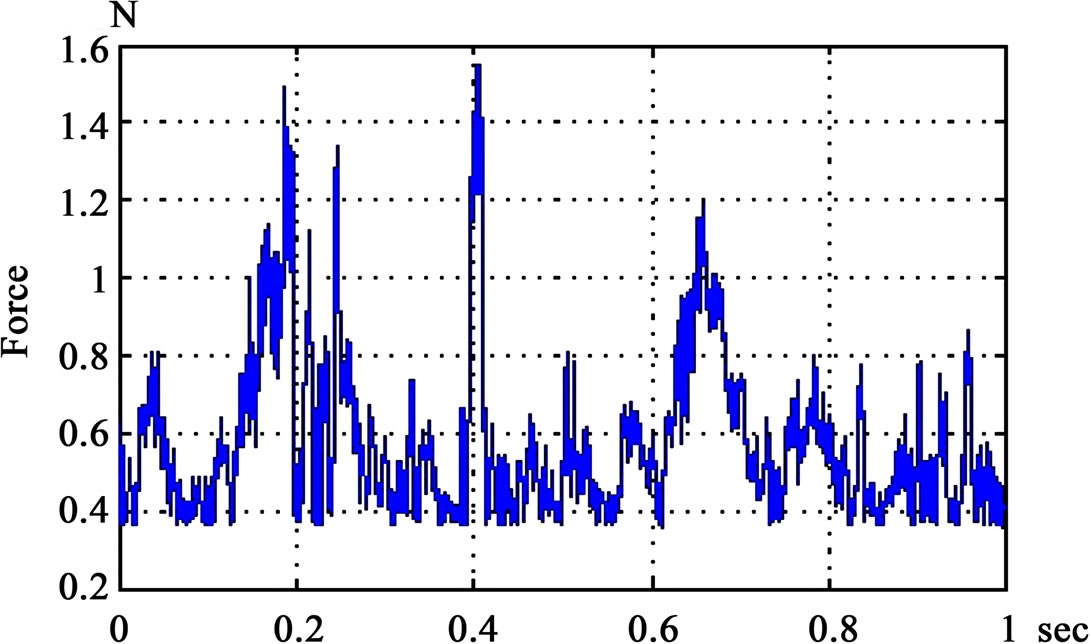
Figure 4. Corresponding wind load acting.
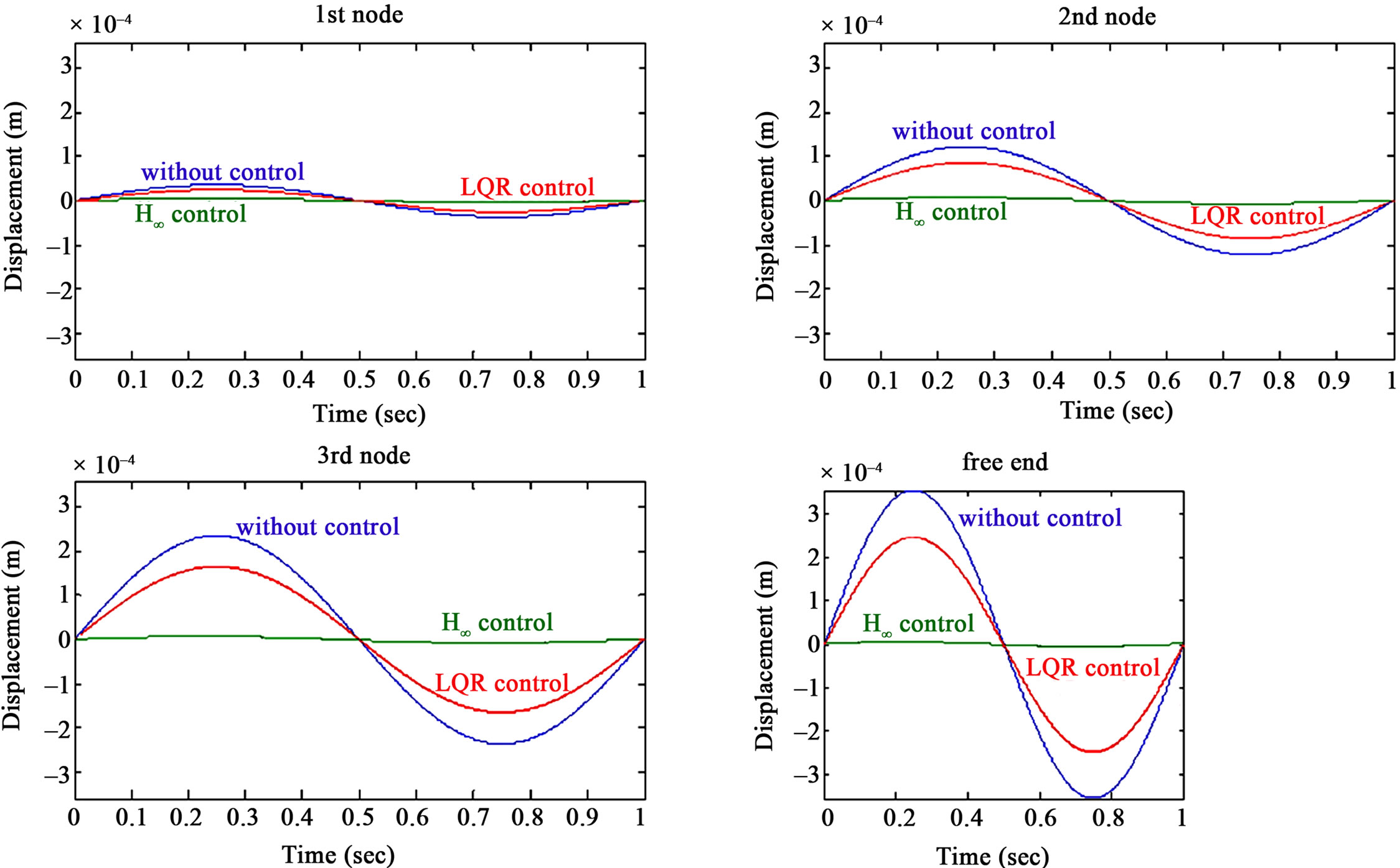
Figure 5. Response of the four nodes for the displacement with LQR and H∞ control and response without control.
controlled beam with LQR control [12,13] and 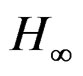 control [14,19], for the four nodes of the beam. Figure 6 shows the dynamical response for the rotations of the uncontrolled and controlled beam with LQR control and
control [14,19], for the four nodes of the beam. Figure 6 shows the dynamical response for the rotations of the uncontrolled and controlled beam with LQR control and  control strategy, for the four nodes of the beam. The beam with
control strategy, for the four nodes of the beam. The beam with  control keeps in equilibrium and we have zero ddisplacements, complete vibration reduction is achieved. The comparison of the open and closed loop frequency response of the system are shown in Figure 7, as shown in figure, there is a significant improvement in the effect of disturbance on error up to the frequency of 1000 Hz. Figure 8 shows the control voltages for the four nodes of the beam. The control voltages for the disturbance rejections of the beam are less than 500 volt.
control keeps in equilibrium and we have zero ddisplacements, complete vibration reduction is achieved. The comparison of the open and closed loop frequency response of the system are shown in Figure 7, as shown in figure, there is a significant improvement in the effect of disturbance on error up to the frequency of 1000 Hz. Figure 8 shows the control voltages for the four nodes of the beam. The control voltages for the disturbance rejections of the beam are less than 500 volt.
Comparison with the open loop response for the same plant shows the good performance of the  controller. Results are very good, and the beam remains in equilibrium. Reduction of vibrations is observed, while piezoelectric add-ons produce voltage within their tolerance limits (±500 volt).
controller. Results are very good, and the beam remains in equilibrium. Reduction of vibrations is observed, while piezoelectric add-ons produce voltage within their tolerance limits (±500 volt).
Then a typical wind load (Figure 4) acting on the side of the structure. The wind load is a real life wind speed measurements in relevance with time that took place in Estavromenos of Heraklion Crete. We transform the wind speed in wind pressure with,
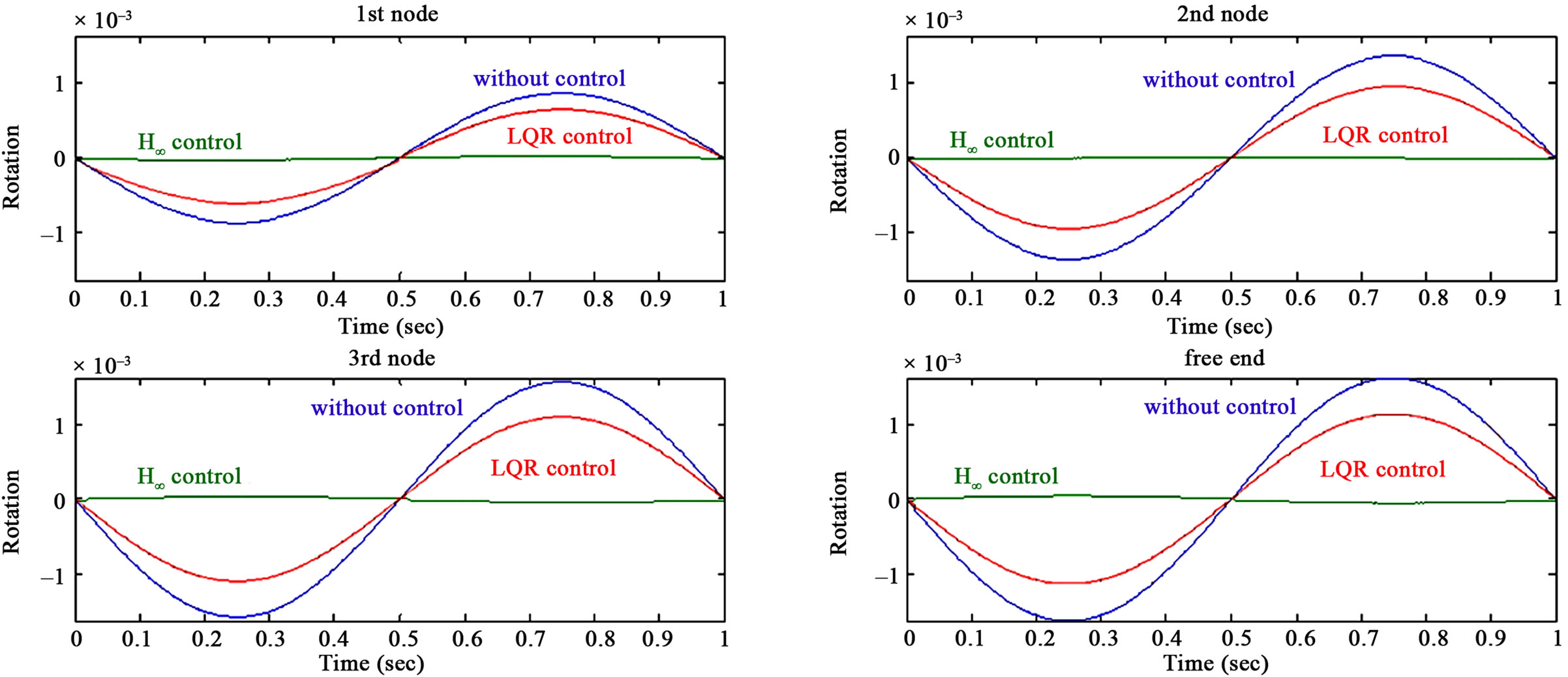
Figure 6. Response of the four nodes on the vibrating beam for the rotation with LQR and H∞ control and without control.

Figure 7. Singular value for H∞ control strategy.

Figure 8. Control profile for the four nodes with H∞ control strategy.
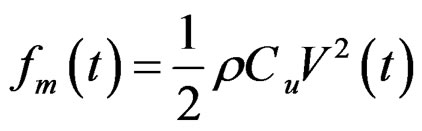 (29)
(29)
where V = velocity, ρ = density and Cu = 1.5.
In Figure 9 the structural displacement responses are reported, for the four nodes of the beam. It is possible to see clearly the benefit induced the control on the maximum value of these displacements. 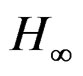 controller results are very satisfactory and prove that
controller results are very satisfactory and prove that 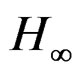 control can reduce smart structures vibrations. In Figure 10 we can see the structural rotations for the four nodes of the beam. The beam with
control can reduce smart structures vibrations. In Figure 10 we can see the structural rotations for the four nodes of the beam. The beam with 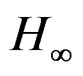 control keeps in equilibrium and we have almost zero displacements.
control keeps in equilibrium and we have almost zero displacements.
In Figure 11 we can see the control profile for the four nodes of the beams. As we can see the voltage is more less than 500 Volt, which is the piezoelectric limit.
4.2. Reduced Order Control
The H∞ controller found is of order 24. The fact that controller order, which is equal to the order of the system, is relatively higher than the order of classical controllers such as LQR has led a number of researchers to develop order reduction algorithms. The most widely used such algorithm, known as HIFOO, has been implemented in a Matlab environment, and is the one used in the following procedure [17,20].
The general problem is to compute a controller of reduced order n < 24 while retaining the performance of the H∞ criterion as well as the behaviour of a full order
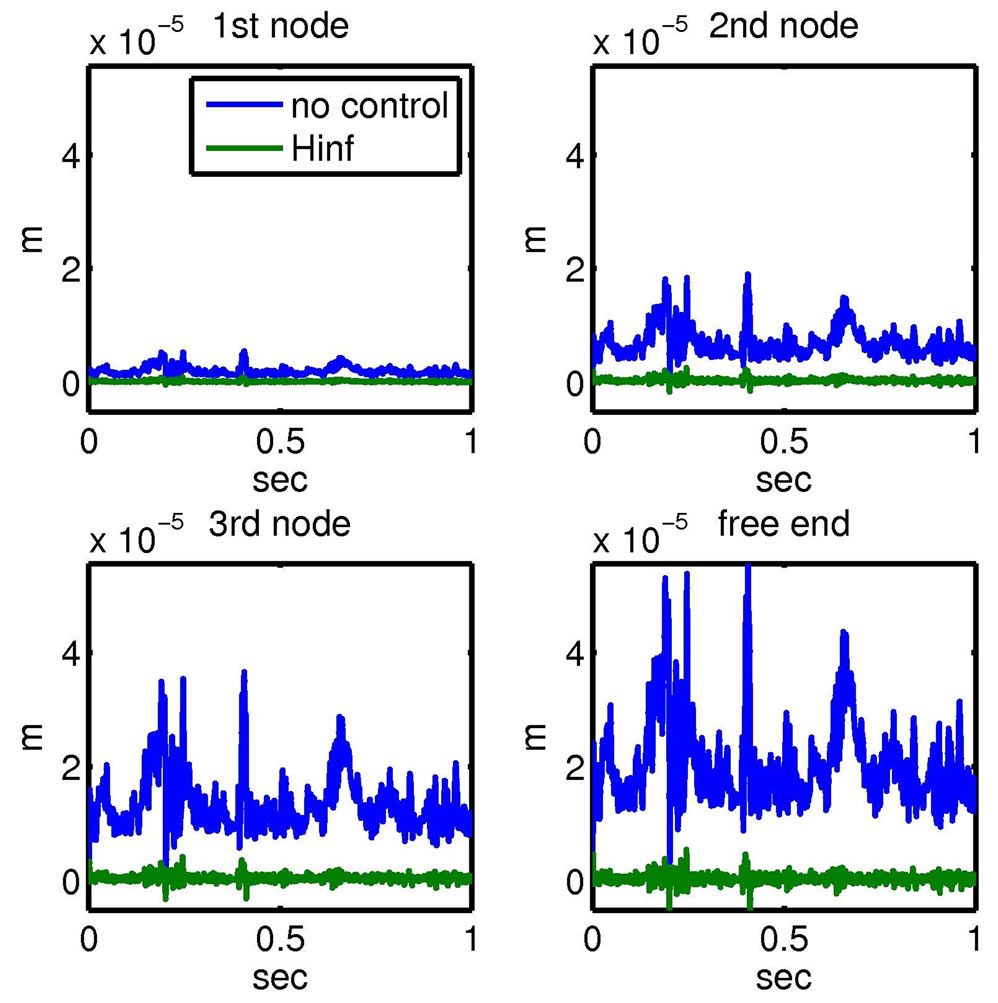
Figure 9. Responses of the four nodes of the beam without and with H∞ control.
controller for the given system [17,20].
Nonsmooth variation analysis and related computational methods are powerful tools that can be effectively applied to identify local minimizes of nonconvex +optimization problems arising in fixed-order controller design. Our computational methods found a 24th order controller that stabilized the system. Using the Matlab package HIFOO we can reduce this controller and stabilize the system with a 2nd order controller without diffi-
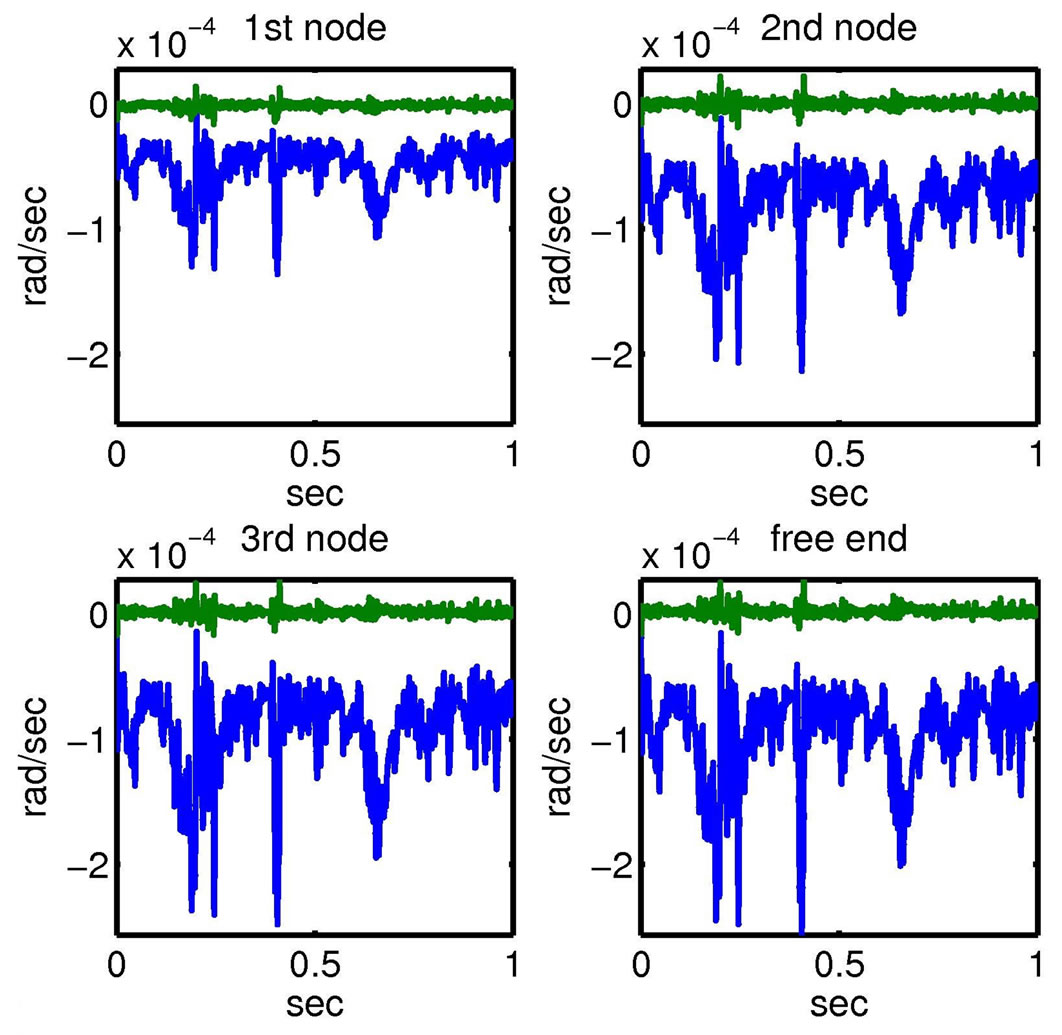
Figure 10. Rotations of the four nodes of the beam without and with H∞ control.
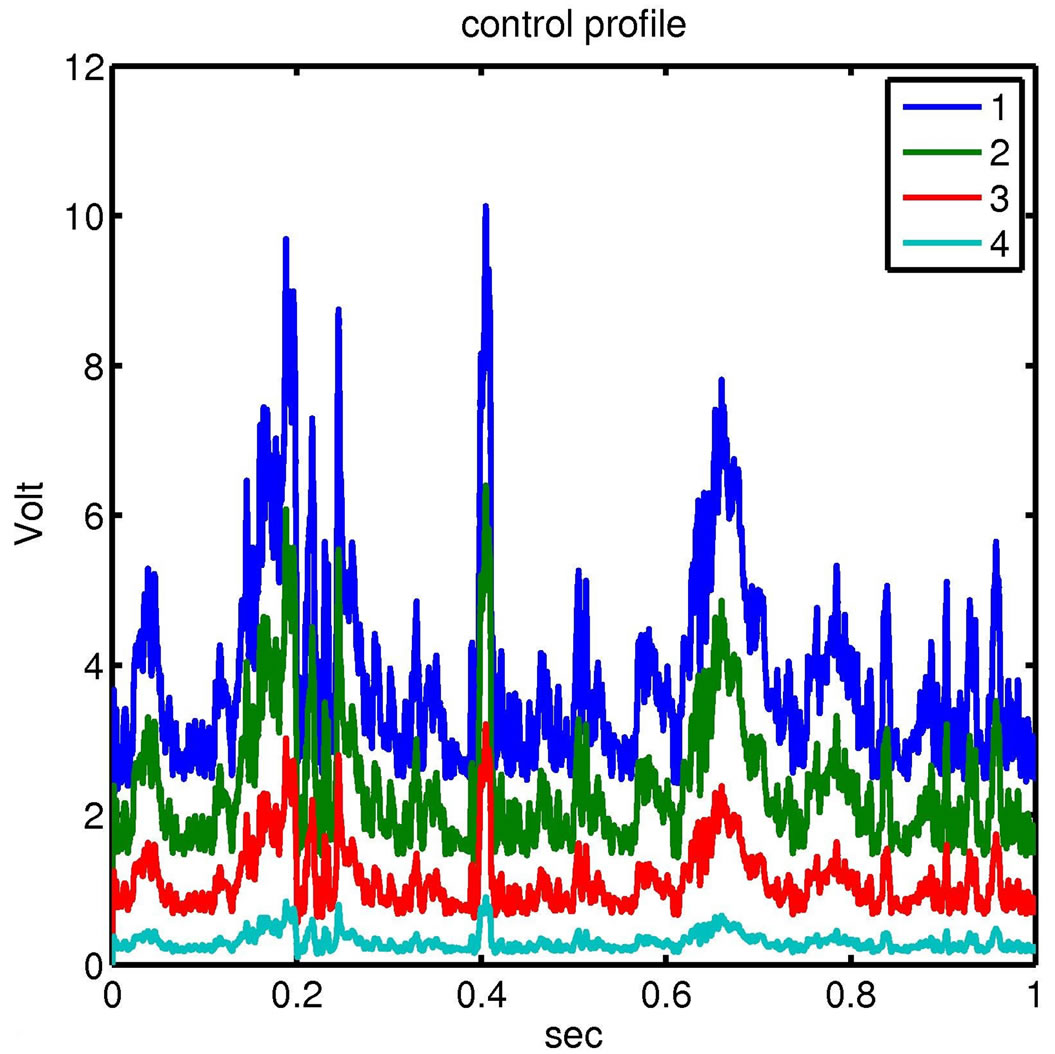
Figure 11. Control voltages for the four nodes of the beam using H∞ control.
culty, suggesting explicit formulas for the controller and for the closed loop system. Furthermore, our analytical techniques prove that this controller is locally optimal in the sense that there is no nearby controller with the same order for which the closed loop system has all its poles further left in the complex plane [20].
These approaches can be extended in order to take into account other key quantities of great practical interest, such as optimization of  performance. In particular, with the help of a MATLAB toolbox called HIFOO (
performance. In particular, with the help of a MATLAB toolbox called HIFOO (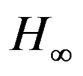 Fixed Order Optimization) we can reduce the order of the controller and have very good results. Figure 12, shows the response of the uncontrolled and control beam of the free end of the beam, using hifoo controller (a second order controller). Figure 13 shows the control voltages for the four nodes of the beam [20]. As we can see we need less energy then the 24th controller for reduced vibrations.
Fixed Order Optimization) we can reduce the order of the controller and have very good results. Figure 12, shows the response of the uncontrolled and control beam of the free end of the beam, using hifoo controller (a second order controller). Figure 13 shows the control voltages for the four nodes of the beam [20]. As we can see we need less energy then the 24th controller for reduced vibrations.
5. Conclusion
A mathematical formulation and finite element model for the vibration suppression of a cantilever beam with piezoelectric laminated surface and viscous layers and elastic core is presented in this paper. The design of the piezoelectric active control using LQR strategy and 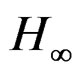 control theory for the nominal and damaged sandwich beam has been studied. The numerical results show that the
control theory for the nominal and damaged sandwich beam has been studied. The numerical results show that the 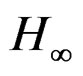 control strategy is very effective and suppresses the vibrations of the beam. The vector of active control forces
control strategy is very effective and suppresses the vibrations of the beam. The vector of active control forces
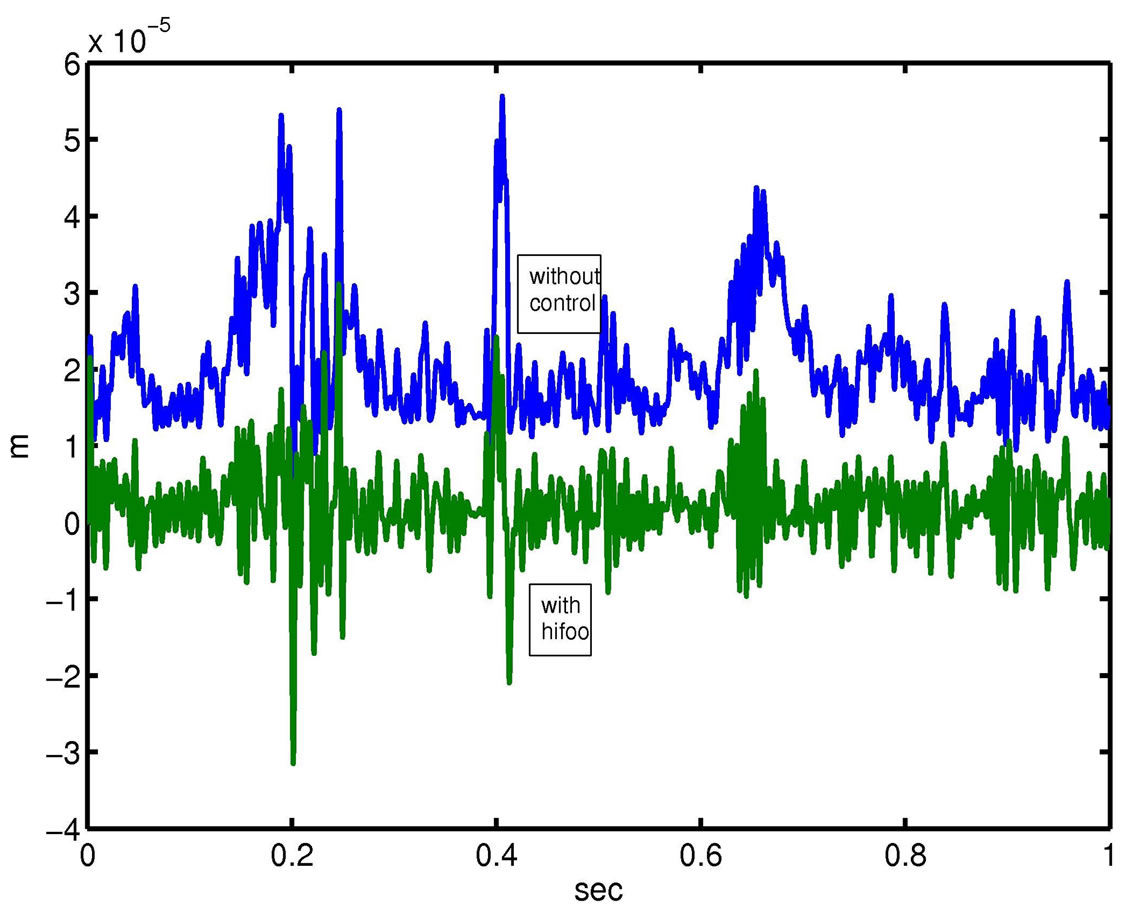
Figure 12. Displacement of the free end of the beam without and with hifoo controller.
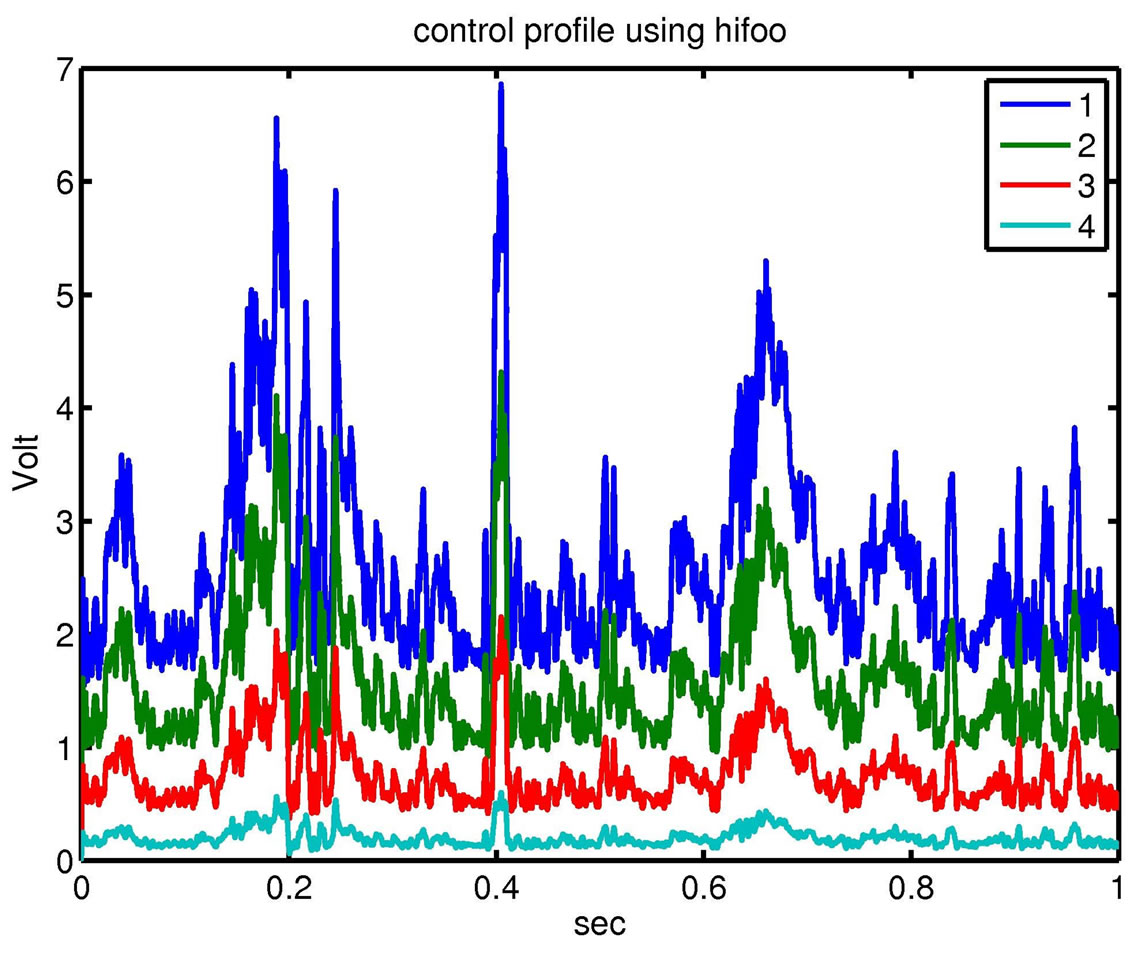
Figure 13. Control voltages for the four nodes of the beam using hifoo controller.
subjected to  performance criterion and satisfying the systems dynamic equations such that to reduce the wind excitations is determined. High robust performance and robust stability are achieved. This work clearly demonstrates the advantages of using advanced robust control theory for the design of practical smart structure.
performance criterion and satisfying the systems dynamic equations such that to reduce the wind excitations is determined. High robust performance and robust stability are achieved. This work clearly demonstrates the advantages of using advanced robust control theory for the design of practical smart structure.
6. Acknowledgements
The authors would like to thank the Wind Energy and Synthesis of Energy Systems Laboratory, of the Technological Educational Institute of Crete, for their offer on real life wind speed measurements in relevance with time that took place in Estavromenos of Heraclion Crete.
REFERENCES
- K. G. Arvanitis, E. C. Zacharenakis, A. G. Soldatos and G. E. Stavroulakis, “New Trends in Optimal Structural Control. Selected Topics in Structronic and Mechatronic System,” World Scientific Publishers, Singapore, 2003, pp. 321-415. doi:10.1142/9789812795526_0008
- G. Foutsitzi, D. Marinova, E. Hadjigeorgiou and G. Stavroulakis, “Robust H2 vi Bration Control of Beams with Piezoelectric Sensors and Actuators,” Proceedings of Physics and Control Conference (PhyCon03), St. Petersburg, Vol. I, 20-22 August 2003, pp. 158-163.
- G. Foutsitzi, D. Marinova, E. Hadjigeorgiou and G. Stavroulakis, “Finite Element Modelling of Optimally Controlled Smart Beams,” 28Ih Summer School: Applications of Mathematics in Engineering and Economics, Sozopol, Bulgaria, 2002.
- B. Miara, G. Stavroulakis and V. Valente, “Topics on Mathematics for Smart Systems,” Proceedings of the European Conference, Rome, 26-28 October 2006, World Scientific Publishers, Singapore, 2007.
- G. E. Stavroulakis, G. Foutsitzi, E. Hadjigeorgiou, D. Marinova and C. C. Baniotopoulos, “Design and Robust Optimal Control of Smart Beams with Application on Vibrations Suppression,” Advances in Engineering Software, Vol. 36, No. 11-12, 2005, pp. 806-813.
- H. F. Tiersten, “Linear Piezoelectric Plate Vibrations,” Plenum Press, New York, 1969.
- N. Zhang and I. Kirpitchenko, “Modelling Dynamics of a Continuous Structure with a Piezoelectric Sensor/Actuator for Passive Structural Control,” Journal of Sound and Vibration, Vol. 249, No. 2, 2002, pp. 251-261. doi:10.1006/jsvi.2001.3792
- T. T. Soong and G. D. Manolis. “Active Structures,” ASCE Journal of Structural Engineering, Vol. 113, No. 11, 1987, pp. 2290-2302. doi:10.1061/(ASCE)0733-9445(1987)113:11(2290)
- M. D. Symans and M. C. Konstantinou, “Semi-Active Control System for Seismic Protection of Structure: A State-of-the-Art Review,” Engineerings Structures, Vol. 21, No. 6, 1999, pp. 469-487. doi:10.1016/S0141-0296(97)00225-3
- M. Anjanappa and J. Bi, “Magnetostrictive Mini Actuators for Smart Structures for Smart Structure Applications,” Int. J. Smart Materials and Structures, Vol. 3, No. 4, 1994, pp. 383-390. doi:10.1088/0964-1726/3/4/001
- K. Chandrashekara and S. Varadarajan, “Adaptive Shape Control of Composite Beams with Piezoelectric Actuators,” Intelligent Materials Systems and Structures 8, 1997, pp112-124e IEEE EMBS, San Francisco, 1-5 September 2004, pp. 2758-2761.
- O. Bosgra and H. Kwakernaak, “Design Methods for Control Systems,” Course notes, Dutch Institute for Systems and Control, Vol. 67, 2001.
- A. Packard, J. Doyle and G. Balas, “Linear, Multivariable Robust Control with a μ Perspective,” ASME Journal of Dynamic Systems, Measurement and Control, 50th Anniversary Issue, Vol. 115, No. 2b, 1994, pp. 310-319.
- B. A. Francis, “A Course on H∞ Control Theory,” SpringerVerlag, Berlin, 1985.
- J. Friedman and K. Kosmatka, “An Improved Two Node Timoshenko Beam Finite Element,” Computer and Structures, Vol. 47, No. 3, 1993, pp. 473-481. doi:10.1016/0045-7949(93)90243-7
- A. Moutsopoulou, A. Pouliezos and G. E. Stavroulakis, “Modelling with Uncertainty and Robust Control of Smart Beams,” In: B. H. V. Topping and M. Papadrakakis, Eds., Proceedings of the Ninth International Conference on Computational Structures Technology, Paper 35, Civil Comp Press, Stirlingshire Scotland, Civil Comp Press, 2008. doi:10.4203/ccp.88.35
- J. V. Burke, D. Henrion and M. L. Lewis, “Overton HIFOO-a MATLAB Package for Fixed-Order Controller Design and Hinf. Optimization,” Proceedings of the IFAC Symposium on Robust Control Design, Toulouse, 2006. www.cs.nyu.edu/overton/software/hifoo
- C. Sisemore, A. Smaili and R. Houghton, “Passive Damping of Exible Mechanism System: Experimental and Finite Element Investigation,” The 10th World Congress of the Theory of Machines and Mechanisms, Oulu, Vol. 5, 1999, pp. 2140-2145.
- A. Pouliezos, “Mimo Control Systems,” Class Notes. http://pouliezos.dpem.tuc.gr
- J. V. Burke, D. Henron, A. S. Kewis and M. L. Overton, “Stabilization via Nonsmooth, Nonconvex Optimization,” IEE Automatic Control, Vol. 5, No. 11, 2006, pp. 1760- 1769. doi:10.1109/TAC.2006.884944

