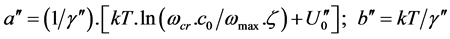Modern Mechanical Engineering
Vol.06 No.04(2016), Article ID:72449,22 pages
10.4236/mme.2016.64013
A Statistical Theory of the Damage of Materials
Georgi Zachariev
Bulgarian Academy of Sciences, Sofia, Bulgaria

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 20, 2016; Accepted: November 27, 2016; Published: November 30, 2016
ABSTRACT
A statistical theory of disperse damage of materials gained under loading is proposed. It is based on the idea of distribution of potential damage spots within a specimen similar to the distribution of the strength values found by testing a set of identical specimens. A relation between damage risk and the probability of damage of a single specimen is assumed. It conforms to the relation between risk and probability of strength distribution of a set of identical specimens, according to Weibull’s statistical theory of material strength. The damage risk just like the damage probability are assumed to be functions of loading and time. Damage is modeled regarding two mechanisms―thermo-fluctuation damage based on the kinetic theory of material strength, and damage depending on a parameter called loading degree (percentage), which depends on load and time. The first mechanism adopts two relations regarding energy barrier reduction due to loading. Equations of damage advance under short-term loading (with a constant rate of load increase) and under long-term (constant) loading are derived. Theoretical relations of damage development are compared with experimental evidence gained via specific tests on short glass fibre reinforced polyoximethylene. The damage itself consists of the accumulation of additional internal surfaces within the entire material volume as measured by small angle scattering X-ray refractometry. It is shown that the mechanism of damage as a function of loading degree where time participates implicitly, gains advantage over the kinetic mechanism where time is explicitly present. The cumulative functions derived for damage accumulation can be used to assess not only damage, but also for statistical analysis of the strength and other quantities.
Keywords:
Damage Mechanics, Mechanical Testing, Non-Destructive Testing

1. Introduction
Two mechanical processes proceed in materials under loading: deformation and fracture. Whereas the deformation can be measured on any kind of basis, the registration of fracture kinetics is a much more difficult problem. This is the reason why one would perform mechanical investigations, usually assessing not the fracture process itself but recording such integral values as strength and time to fracture―results of fracture development. This is also the reason for the introduction of some internal parameter whose physical meaning is not clear but which is to describe the damage process. Note however that there are other approaches which indirectly assess damage by registering the change of some mechanical or geometrical macrovalues, i.e. also without clear physical meaning.
The aim of this work is to derive equations approximating the damage process. Under damage we shall understand the accumulation of additional internal surfaces (micro, mezzo and macro cracks, debondings, pores) in the entire material volume due to the loading i.e. the dispersed damage in our work has a clear physical meaning. A statistical theory is developed for that purpose. The idea of Weibull for a connection between risk and probability of fracture is used. A damage model is proposed where these two quantities are assumed to be functions of loading and time. It is also assumed that potential places (spots) of damage exist within the entire material volume. Two mechanisms of spot fracture are investigated: A thermo-fluctuation one and a mechanism where spot fracture is determined by an especially defined parameter.
2. Damage Model
The notable researcher W. Weibull, in his work on strength of materials published in 1939 [1] , made no other assumption but that there exists a cumulative function of the distribution of the strength of identical specimens. Its derivative with respect to strength is the distribution function. Furthermore, Weibull concluded that “it is obvious that the distribution curve should not be influenced and distorted by alien factors independent of the specimen itself, as for instance method of measurement, measuring instruments, fixation of the test specimens, etc., but that it should be an expression of the strength properties of the material”.
A key point of Weibull’s theory is the introduction of the term “risk of rupture” R (referred to as “risk” for brevity in what follows), involving a cumulative function of strength distribution W (Weibull denoted quantities R and W, depending on strength , by B and S, respectively, in his work). The link between R and W is given by the equation:
, by B and S, respectively, in his work). The link between R and W is given by the equation:
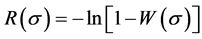 (1)
(1)
Function 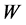 is the probability of specimen fracture at stress
is the probability of specimen fracture at stress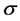 . Here a natural logarithm is used instead of a common logarithm used in [1] .
. Here a natural logarithm is used instead of a common logarithm used in [1] .
Assume that damage develops due to the existence of different potential places― spots in the material, which become active (i.e. unleash damage) depending on stress 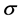 and time t. Assume also a link between risk of damage
and time t. Assume also a link between risk of damage 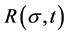 and damage probability
and damage probability 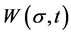 in a form identical to that in (1):
in a form identical to that in (1):
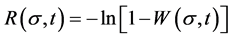 (2)
(2)
Regardless of whether we consider strength or damage, the dependence between risk R and probability W is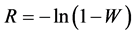 ―see Figure 1(a). For zero probability W, risk R is also zero while for
―see Figure 1(a). For zero probability W, risk R is also zero while for 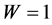 (i.e. 100% probability) risk
(i.e. 100% probability) risk
For low probability, risk R is approximately equal to probability W, i.e. R ≈ W (Figure 1(b)).
Despite the identical forms, Equations ((1) and (2)) significantly differ from each other: Equation (1) presents the distribution of strength of a set of identical specimens while Equation (2) sets forth the distribution of damage spots within the material, i.e.
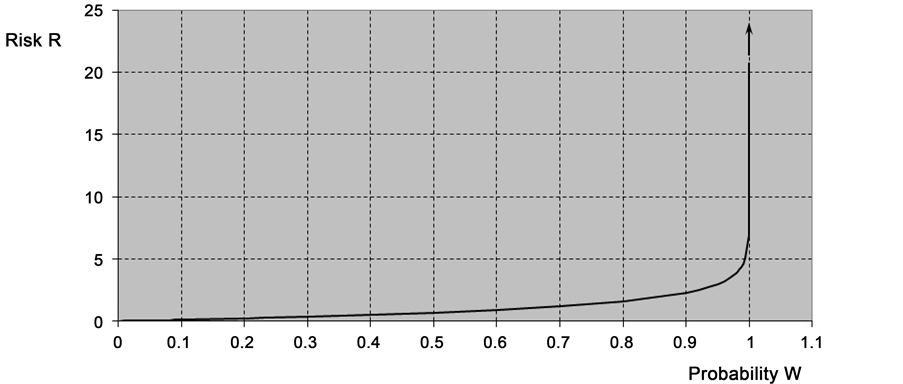

Figure 1. (a) Dependence of the risk R on the probability W; (b) dependence of the risk on the probability at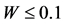 ;
; .
.
within each specimen.
Assume the following relation for damage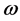 :
:
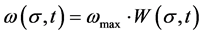 (3)
(3)
where 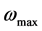 is the maximal possible damage when all potential damage spots are activated i.e. fractured.
is the maximal possible damage when all potential damage spots are activated i.e. fractured.
Consider two loading types: short-term loading with constant rate of stress increase and long-term loading with constant stress (so called regime of creep).
Time and load can be introduced in risk 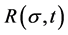 based on two mechanisms of spot fracture:
based on two mechanisms of spot fracture:
- a thermo-fluctuation mechanism where heat fluctuations play a decisive role in damage occurrence (spot fracture);
- a mechanism where spot fracture is determined by a parameter depending on time, load and rate of load increase;
3. Thermo-Fluctuation Mechanism of Damage (Mechanism I)
The thermo-fluctuation mechanism of damage lies within the basis of the kinetic theory of fracture [2] , developed in the Ioffe institute (St Petersburg―Russia). According to this theory heat fluctuations play a major role in damage accumulation. Mechanical stress only decreases the energy barrier that heat fluctuations should overcome to instigate fracture.
Ref. [2] treats break of an interatomic bond with an energy barrier 






where 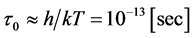
Based on break of the interatomic bonds, we assume the following model of damage accumulation: there exist potential damage spots in the material having identical energy barriers

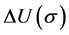
Thermal fluctuations with energy 





where 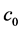

The hazardous heat fluctuations, i.e. those yielding fracture of spots, read:

The frequency of occurrence of hazardous fluctuations is 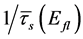

The total frequency of the occurrence of hazardous fluctuations 


where 
It follows from (7) that the account for all possible hazardous heat fluctuations increases the frequency of damage generation by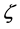
Assume that risk 

Considering (5) and (7), it follows for long-term loading (σ = const.) that:

Assume for
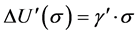
or

Pursuant to (9a) 




According to (9a) we have for
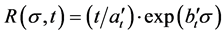
where 

According to (9b) we have for 

where 

Consider a short time of stress increase with a constant rate


For


For


4. Damage as Dependent on a Specified Loading Parameter (Mechanism II)
Assume a mechanisms of damage where damage spot activation (i.e. spot fracture and damage generation) takes place depending on a specific loading parameter p. Assume also that a curve of spot distribution exists, which is a function of that parameter: some spots fracture under smaller values of p, while others―under larger values of p.
Adopt loading degree (percentage) as a loading parameter, defined as follows:
- for short-term loading (index K) under constant stress rate

where 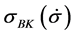

- for long-term loading (index L) under constant stress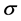
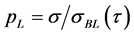
where 

Assume a linear relation between the long-term strength and the logarithm of durability, i.e.:
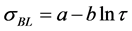
where a and b are coefficients.
The degree of loading p specifies a relation between stress acting at a specific time and material fracture stress regarding the same conditions (i.e. rate of stress increase during short-term loading and time of stress application during long-term loading). It follows from (13) and (14) that p is a function of time for both loading types.
As for the function of the risk of damage 


where 

The choice of a power or exponential form of risk 

5. Functions of Damage Accumulation
The cumulative functions of damage 

The accuracy of the approximation in (17) is as greater as 

Mechanism I
Short-term loading
? with R following (11):

where

? with R following (12):

where

Long-term loading
? with R following (8) and (9а):
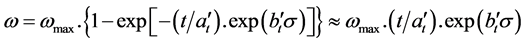
? with R following (8) and (9b):
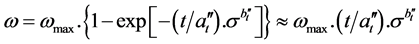
Consider relations (20) and (21) and a macrofracture criterion stating that fracture occurs when critical damage 



according to (20):
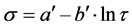
according to (21):

where:
i.e. linear relations between the durability logarithm and the constant stress (its logarithm, respectively) are derived.
Mechanism II
Consider both loading types (long-term and short-term ones) and relations (17), (15) and (16). Then, it follows that:
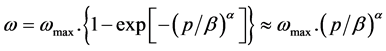

where p is presented by (13) for short-term loading, and by (14)-for long-term loading.
The comparison between the cumulative functions of damage, considering both mechanisms, shows the following specificities:
- Functions 
- Functions 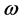

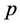
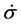



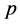
- The assumption of the form of 
To compare damage accumulation found pursuant to both mechanisms, we shall present 
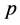
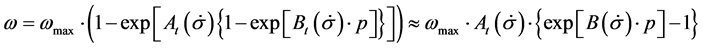
where:

and 


where:

and 

The cumulative function (19а), as well as that in (19) are similar to Weibull’s function, but having parameters depending on

where 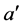


where 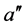
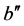
6. Experimental Verification of the Cumulative Functions
The experimental verification of the cumulative functions pursuant to mechanism I- (18а), (19а), (20а), (21а) and mechanism II-(22) and (23) requires the performance of specially designed experiments in order to register damage development for both loading regimes-short-term and long-term ones.
Assume that damage 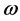
6.1. Material
The material is injection moulded polyoximethylene reinforced by means of short glass fibers. Samples, produced by Ticona GmbH Frankfurt a.M. in compliance with DIN EN ISO 527, are characterized with glass fibre (E-glass) part 26 wt%, mean fibre length 320 μm (max. 800 mm, min. 60 mm) and fibre diameter 10 ± 1 μm. Silane compounds are used for fiber adhesion dressing.
6.2. Mechanical Loading
Samples for a short-term tests were subjected to tension on an Instron testing machinery. Tension was parallel to the oriented short fibres, applying three constant loading rates dF/dt = 0.22; 1.1 and 5.5 [kN/min] i.e. 0.093; 0.465 and 2.326 [MPa/sec] respectively. After attaining different loading steps―50%, 70%, 80%, 85%, 90%, 93%, 95%, 97% and 98% of the force-at-fracture
Samples for a long-term tests are loaded by constant tension, using lever loading devices type “Frank”. Load is uniformly fed via a hydraulic jack until attaining a specific value.
To find material long-term strength, time prior to sample fracture is measured applying the following constant loads: 71.88 [MPa]; 82.32 [MPa]; 92.75 [MPa]; 100.6 [MPa]; 108.3 [MPa]. Three samples are tested under each load.
The process of creep damage accumulation is experimentally investigated for 3 degrees of constant loading: 64.06 [MPa], 74.56 [MPa] and 82.24 [MPa], and within three samples per each load. After 2 [h], 4 [h], 6 [h], 24 [h] and 48 [h], respectively, samples are unloaded and accumulated damage is measured.
6.3. Damage Processes and Their Measurement
Damage processes develop in two directions: accumulation of micro and mezzo cracks perpendicular to loading (Figure 2(b)) and accumulation of micro and mezzo fibre/matrix debondings parallel to the loading direction (Figure 2(a)). Damage takes place into the whole material volume. In what follows we denote the two kinds of damage as cracks and debondings, respectively. A damage process proceeds relatively homogeneously in isolated volumes until there is interaction between them and than it spreads to the macrovolume leading to collapse (i.e. to material splitting caused by a macrocrack).
The method of damage measure uses the effect of refraction at very small angles of few arc minutes. The scattered intensity of this refraction is by several magnitudes higher than that of conventional X-ray scattering (diffraction at larger angles).
The internal surfaces inherent to the two types of damage are measured by an appropriate guidance of the X-ray beam (Figure 2(a), Figure 2(b)). In the both cases the scattering plane (the plane determined by the collimated beam and the refracted one) is perpendicular to the plane of the inner surfaces. The planes of cracks are also perpendicular to the loading direction (Figure 2(b)), those of debondings are parallel to it (Figure 2(a)).
Quantity 
Figure 2. An X-ray beam with cross section 3 mm/50 μm scans an area 10 mm/20 mm, with a horizontal step 1 mm and vertical step 0.2 mm. So the next measurement partially overlaps the previous one. As an example, Figure 3 and Figure 4 show the distribution of single refractions cd measured by scanning loaded-unloaded samples and applying up to 98% of the fracture load, as well as refraction distribution in a virgin sample.
Figure 3. X-ray refraction topograms of loaded-unloaded up to 98% of fracture load samples and virgine sample. 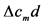

Figure 4. X-ray refraction topograms of loaded-unloaded up to 98% of fracture load samples and virgine sample. 

of damage within the volume corresponding to the scan area. All measurements shown in each of these figures are included in only one point of diagrams that follow―namely loading step 98% of the force-at-fracture. The same procedure was done for every loading step. Damage was registered by Mr. Heinz Ivers in the Federal Institute of Materials Research and Testing (BAM―Berlin).
The mean arithmetic value of the differences 

where m is the mean value of c.
The mean value 


6.4. Experimental Results
Damage accumulation 



Strength depends on the loading rate: it is 115.94 [MPa] at 0.093 [MPa/sec], 124.19 [MPa] at 0,465 [MPa/sec] and 127.72 [MPa] at 2.326 [MPa/sec], i.e. it increases with the loading rate.
It follows from Figure 5 and Figure 6 that the higher the loading degree, the higher the damage. However, this is to be expected. It can be assumed also from these figures that damage depends on the loading degree, only, but not on the loading type―short- or long-term loading. Damage measured after macrofracture at loading rate 0,465 [MPa/sec] and under short-term loading is denoted by + (cross) in Figure 5 and Figure 6. Damage
Figure 5. Experimental data of damage 
Figure 6. Experimental data of damage 
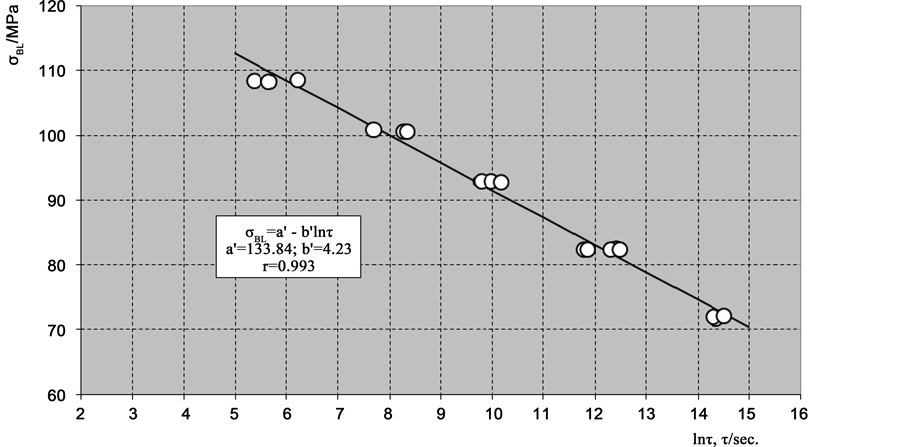
Figure 7. Long-term strength 
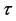
values are less than the extrapolated ones at p = 100% according to measurements on unloaded samples. This fact can be explained with the explosion-like unloading at macrofracture, which is different from the unloading at other experimental points. It causes a greater damage closure.
Long-term strength in creep as a function of specimen lifetime (time to fracture) according to Equations ((20') and (21')) is shown in Figure 7 and Figure 8.
6.5. Approximation of Damage According to Mechanism I
Equations ((18a) and (19a)) describe damage accumulation under short-term loading,
Figure 8. Logarithm of the long-term strength 

while Equations ((20a) and (21a))―that under long-term loading. There are two coefficients to be determined in these equations:






Figure 9 and Figure 11 show regression results for cracks and debondings respectively. For other loading rates and their corresponding strength, damage accumulation is calculated according to Equations ((18a) and (19a)) and plotted by solid and dashed lines respectively. Index K denotes short-term loading, index L―long-term one.
It follows from Figure 9 and Figure 11, that the calculated damage at 
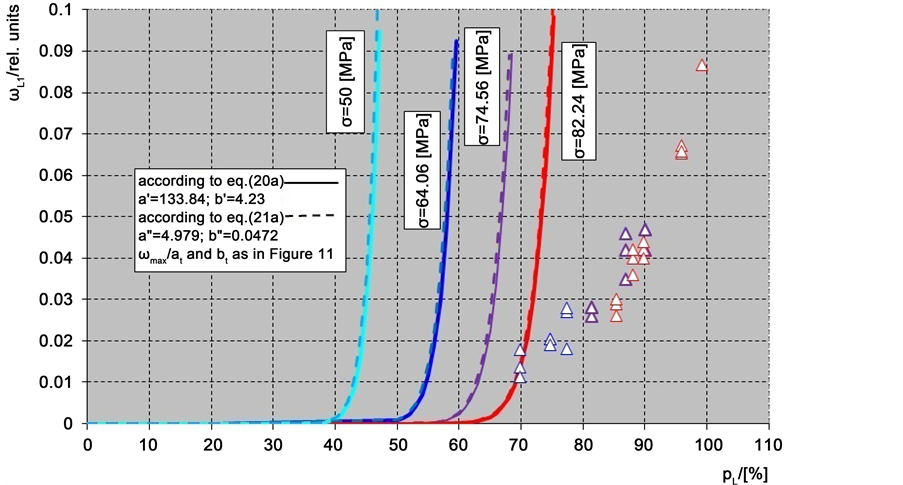
Figure 10 and Figure 12 show approximations of damage accumulation under long-term loading for cracks and debondings respectively. Solid lines present approximations according to Equation (20a) and dashed ones―according to Equation (21a). The coefficients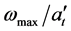







It follows from Figure 10 and Figure 12 that the calculated damage presented as a function of loading degree at four constant stresses does not agree with the experimental data.
6.6. Approximation of Damage According to Mechanism II
Equations ((22) and (23)) describe damage accumulation under short- and long-term loading. Loading degree in these equations is calculated according to (13) for short- term loading and according to (14)―for long-term loading.
Figure 13 and Figure 14 show approximations of all experimental data for cracks, while Figure 15 and Figure 16―data approximations for debondings. The coefficients in (22) were found performing an exponential regression with iteration, while those in (23)―performing a power regression.
Figure 9. Damage 
Figure 10. Damage 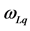
Figure 11. Damage 
Figure 12. Damage 
Figure 13. Damage 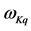
Figure 14. Damage 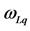
Figure 15. Damage 
Figure 16. Damage 
It follows from Figures 13-16, that the approximations employing both Equations ((22) and (23)) are very good. Comparison shows that the approximation according to Equation (22) is better (the correlation coefficients are larger) than the approximation according to Equation (23). The same result was found in [7] for damage mean values at every p.
7. Other Applications of the Cumulative Functions
The cumulative functions derived to approximate damage―Equations ((22) and (23)), can also be used in statistical data processing. For that purpose, substitute damage 



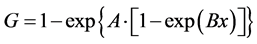
Equations ((22') and (23')) may be employed to approximate the cumulative functions of the bending strength of float glass [8] (Figure 17), lifetime of electron tubes [8] (Figure 18) and lifetime of turbine engines [9] (Figure 19). Large correlation coefficients are found.
Figure 17. Cumulative distribution function of G. Bending strength of float glass, example 1 from [8] .
Figure 18. Cumulative distribution function of G. Lifetime of electron tubes, example 2 from [8] .
Figure 19. Cumulative distribution function of G. Lifetime of turbine engines, example from [9] .
8. Conclusions
1) A statistical theory of disperse damage of materials gained under loading is proposed. It is based on the idea of distribution of potential damage spots within a specimen similar to the distribution of the strength values found by testing a set of identical specimens. A relation between damage risk and the probability of damage of a single specimen is assumed. It conforms to the relation between risk and probability of strength distribution of a set of identical specimens, according to Weibull’s statistical theory of material strength.
2) Damage is modeled regarding two mechanisms―thermo-fluctuation damage based on the kinetic theory of material strength, and damage depending on a parameter called loading degree (loading percentage), which depends on load and time. The first mechanism adopts two relations regarding energy barrier reduction due to loading. Equations of damage advance under short-term loading (with a constant rate of load increase) and under long-term (constant) loading are derived.
3) Compare the theoretical relations of damage development with experimental evidence gained via specific tests. It is seen that the mechanism of damage as a function of loading degree where time participates implicitly, gains advantage over the kinetic mechanism where time is explicitly present. To approximate damage, one should use Equations ((22) and (23)).
4) It can be assumed, that damage depends on loading degree, only, but not on the loading type (short- or long-term loading). This enables one to predict damage under long-term loading based on data on short-term loading, and vice versa.
5) The cumulative functions (22) and (23) can be used to assess not only damage, but also strength and other quantities.
6) It is necessary to verify the proposed theory for other materials. It provides an opportunity to approximate as well as predict the damage process. The equations derived for damage can be applied to a wide range of cases of material response.
Acknowledgements
This work appears thanks to the financial support of the Alexander von Humboldt Foundation (Bonn, Germany) and the fruitful collaboration with the colleagues from the Federal Institute for Materials Research and Testing (BAM-Berlin, Germany): M. P. Hentshel, H.-V. Rudolph, H. Ivers. I thank my colleagues from the Departament 5, Division 5.3 (Mechanics of Polymers) of the BAM for the long-standing support.
Cite this paper
Zachariev, G. (2016) A Statistical Theory of the Damage of Materials. Modern Mechanical Engineering, 6, 129-150. http://dx.doi.org/10.4236/mme.2016.64013
References
- 1. Weibull, W. (1939) A Statistical Theory of the Strength of Materials. Generalstabens Litografiska Anstalts Förlag, Stockholm.
- 2. Regel, V.R., Slutzker, A.I. and Tomashevskii, E.E. (1974) Kinetic Nature of Strength of Solids. Nauka, Moskow. (In Russian).
- 3. Harbich, H.-W., Hentschel, M.P. and Schors, J. (2001) X-Ray Refraction Characterization of Non-Metallic Materials. NDT&E International, 34, 297-302.
https://doi.org/10.1016/S0963-8695(00)00070-0 - 4. Bullinger, O. (2006) X-Ray Methods in the Field of Non-Destructive Testing and Evaluation of Composite Structures. In: Busse, G., Kröplin, B.-H. and Wittel, F.K., Eds., Damage and Its Evolution in Fiber-Composite Materials: Simulation and Non-Destructive Evaluation, SFB 381, ISD Verlag, Stuttgart, 73-80.
- 5. Zachariev, G., Rudolph, H.-V. and Ivers, H. (2004) Damage Accumulation in Glassfibre-Reinforced Polyoximethylene under Short-Term Loading. Composites Part A, 35, 1119-1123.
https://doi.org/10.1016/j.compositesa.2004.03.018 - 6. Zachariev, G., Rudolph, H.-V. and Ivers, H. (2009) Prediction of Creep-Damage Accumulation in Glass Fibre Reinforced Polyoximethylene. Materials Science and Engineering A, 510-511, 425-428.
https://doi.org/10.1016/j.msea.2008.04.114 - 7. Zachariev, G. (2013) Approximation of Damage Accumulation in Fibre Reinforced Polymers. Materials Testing, 55, 32-37.
https://doi.org/10.3139/120.110408 - 8. DIN 55303-7, March 1996.
- 9. Jensen, F. and Petersen, N.E. (1982) Burn-In. John Wiley & Sons, Chichester, New York, Brisbane, Toronto, Singapore.