Modern Mechanical Engineering
Vol.05 No.03(2015), Article ID:58543,17 pages
10.4236/mme.2015.53007
Adaptive Real-Coded Genetic Algorithm for Identifying Motor Systems
Rong-Fong Fung1*, Chun-Hung Lin2
1Department of Mechanical & Automation Engineering, National Kaohsiung First University of Science and Technology, Kaohsiung, Taiwan
2Graduate Institute of Electrical Engineering, National Kaohsiung First University of Science and Technology, Kaohsiung, Taiwan
Email: *rffung@nkfust.edu.tw
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2015; accepted 1 August 2015; published 4 August 2015
ABSTRACT
In this paper, the main objective is to identify the parameters of motors, which includes a brushless direct current (BLDC) motor and an induction motor. The motor systems are dynamically formulated by the mechanical and electrical equations. The real-coded genetic algorithm (RGA) is adopted to identify all parameters of motors, and the standard genetic algorithm (SRGA) and various adaptive genetic algorithm (ARGAs) are compared in the rotational angular speeds and fitness values, which are the inverse of square differences of angular speeds. From numerical simulations and experimental results, it is found that the SRGA and ARGA are feasible, the ARGA can effectively solve the problems with slow convergent speed and premature phenomenon, and is more accurate in identifying system’s parameters than the SRGA. From the comparisons of the ARGAs in identifying parameters of motors, the best ARGA method is obtained and could be applied to any other mechatronic systems.
Keywords:
Adaptive Real-Coded Genetic Algorithm (ARGA), Brushless Direct Current Motor (BLDC), Electrical Fan, Induction Motor, System Identification

1. Introduction
The mechanical commutator of the brushless direct current (BLDC) motor [1] is replaced by electronic switches, which supply current to the motor windings as a function of the rotor position. A BLDC motor is one of the permanent magnetic synchronous motors, and has advantages of simple structure, product easily, and low cost [2] . Due to their favorable electrical and mechanical properties, high starting torque and high efficiency, the BLDC motor are widely used in most servo applications such as actuation, robotics, machine tools, and so on.
Many literatures [3] - [6] have discussed motor operations. For a quality BLDC motor, proper maintenances and applications are important, and inherently more reliable, more efficient, and with current electronics technology, more cost effective than the standard electrical fans and controllers [3] . Therefore, the BLDC motor has advantages of high performance, low noise and long lifespan. The conventional dc motor can be represented by the mathematical model. The technicians often wanted to test the performance or measure the parameters of a motor, and the ordinary differential equations of a motor were solved by Runge-Kutta method [4] [5] . However, the precise of a BLDC motor requires its accurate parameters, which can be measured or estimated. In order to identify parameters of BLDC motors, the genetic algorithms were used to search for precise parameters [6] .
Recently, due to rapid improvements in power devices and microelectronics, the field-oriented control and feedback linearization techniques have increased induction motor drives for high-performance applications possible [7] . Induction motors are the most widely used motors in industry because they are simple to build, rugged, reliable and have good self-starting capability. Many advanced algorithms have been investigated to control induction motors, especially the vector control [8] . To design controllers, nonlinear motor models must be used for identification and optimization. Several methods have been proposed to tackle the problem of induction machine parameter estimation [9] [10] .
Genetic algorithm (GA) is a searching process based on natural selection, and now is used as a tool for searching the large, poorly understood spaces that arise in many application areas of science and engineering [11] . In this method, a large set of configurations forms a population with new generations created by selection, crossover and mutation of the current population. It is hoped that this evolution process can increase the fitness value of the population to a near optimal value. However, conventional GA often has slow convergent speed and premature phenomenon in engineering applications. In order to overcome these shortcomings, many researchers have made great efforts to improve the performance [12] [13] by proposing a variety of programs, such as base on the overall fitness value, average square deviation of population and dual species sub-population etc.
In this paper, the real-coded encoding scheme of fixed length to randomly generate the initial population is used by means of roulette wheel. This standard genetic features by use of only three basic genetic operators: selection operator, crossover operator and mutation operator, simplifies the process of genetic evolution, and easy to be understood. However, the fitness value may occur slow convergent speed and premature phenomenon in a traditional real-coded genetic algorithms (RGA) [14] , and the adaptive genetic algorithm (ARGA) is proposed to solve the problems and to find a solution near to the maximum optimization of the motor system.
This paper is organized as follows. Firstly, the BLDC and induction motors’ equations are established. Secondly, the algorithms in the SRGA and ARGAs are presented and discussed. Thirdly, comparisons between the SRGA and ARGA in numerical simulations and experimental results are discussed and it is concluded that the ARGAs are better than SRGA.
2. Identification Based on the RGA
2.1. Standard Real-Coded Genetic Algorithm (SRGA)
The RGA [15] [16] is an optimization searching algorithm, which simulates evolution mechanism on a computer-based platform in conjunction with natural selection and genetic mechanism. The chromosomes are expressed by vectors and each element of vectors is called a gene. The standard RGA (SRGA) has stationary crossover probability and mutation probability in the evolutional process. If the crossover probability and mutation probability are stationary values, the individual will be lack of diversity in each generation.
2.2. Adaptive Real-Coded Genetic Algorithm (ARGA)
It is important that crossover probability and mutation probability are set for genetic algorithms, the improper settings will cause falling into local optimum algorithms in search and the premature convergence. Therefore, an efficient method for a fast setting is essential. For this point, a mechanism to adjust the crossover probability and mutation probability according to the algorithmic performance is considered [17] . In this paper, the multi-me- thod ARGA for parameters’ identification of the electrical fan system will be employed.
2.2.1. Method 1 of ARGA
In Equations (4) and (5), the crossover probability will be reduced to preserve excellent chromosomes; on the contrary it will be added to evolutionary excellent chromosomes. And then, the mutation probability will be reduced to preserve excellent chromosomes; on the contrary it will increase the diversity of the population and avoid to falling into local optimum [18] . The overall structure of method 1 of ARGA can be described as follows.
A. Encoding: The parameters of the BLDC motor and induction motor are composed by real-coded values.
B. Initialization: A collection of individuals is referred to as a population. A population size of 100 is used to generate final segmentation boundaries.
C. Fitness function: The fitness function is adopted as follows.
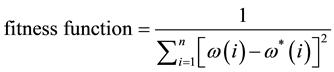 (1)
(1)
where n is the total number of sampling point, 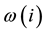 and
and 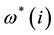 are the rotation speeds by using the identified and assigned parameters in Equations (14) and (15), respectively.
are the rotation speeds by using the identified and assigned parameters in Equations (14) and (15), respectively.
D. Selection: In this stage, the expected time of an individual being selected for recombination is proportional to its fitness value relative to the rest of the population. This operation is to achieve a mating pool with the fittest individuals selected according to a probabilistic rule that allows these individuals to be mated into new populations. The selection is carried out by using the roulette wheel method.
E. Crossover and Mutation: The crossover is the breeding of two parents to produce a single child, who has features from both parents and thus may be better or worse than either parent according to the objective function. The primary purpose of mutation is to introduce variation and help bring back some essential genetic traits, and also to avoid the premature convergence of entire feasible space caused by some super chromosomes [19] .
To reduce the premature convergence and improve convergence rate of the SRGA, the adaptive probabilities of crossover and mutation are presented in the ARGA. The probabilities of crossover  and mutation
and mutation 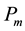 are respectively given as follows.
are respectively given as follows.
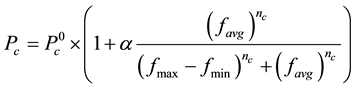 (2)
(2)
 (3)
(3)
where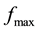 ,
,  and
and 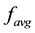 are the maximum, minimum and average individual fitness, respectively,
are the maximum, minimum and average individual fitness, respectively,  and
and 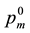 are crossover and mutation of probabilities, respectively and
are crossover and mutation of probabilities, respectively and 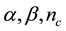 are coefficient factors. In this paper,
are coefficient factors. In this paper, 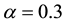 ,
, 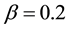 and
and  [20] are taken.
[20] are taken.
From Equations (2) and (3), it is known that the adaptive 



2.2.2. Method 2 of ARGA
The GAs have been extensively used in different domains as a type of robust optimization method. However, the GA to demonstrate a more serious question is a premature convergence problem, less capable local optimization, the late slow convergence and can’t guarantee convergence to the global optimal solution and so on. In recent years, many researches [21] [22] try to improve genetic algorithms, such as improving the encoding scheme, fitness function, genetic operator design. For this reason, the ARGA is proposed with the crossover probability 



where, 



bility; 






As a result, the adaptive 



2.2.3. Method 3 of ARGA
An important problem in usage of the RGA is premature convergence, and the searching process may trap in a local optimum before the global optimum is found. This section employs an ARGA which adjusts mutation probability dynamically based on average square deviation (ASD) of population fitness value, which shows the population diversity to solve the premature problem. From compared analysis, it is shown the proposed ARGA efficiently avoid the premature problem [27] . Premature convergence can also be blamed in [28] by avoiding the loss of critical alleles due to selection and the schemata disruption due to crossover.
The selection operation reduces the diversity of population, the crossover operation does not decrease the diversity of population, and the mutation operation can advance the diversity. Mainly, all these issues produce two effects, the lack of diversity in the population and a disproportionate exploitation or exploration relationship, cause the premature problem [29] . When the ASD becomes smaller or less, it shows that many individuals are becoming as the same, so the mutation probability should be increased to advance the diversity of population for getting global optimal solutions.
A. Selection operator: The selection is carried out using the roulette wheel method in this paper.
B. Crossover operator: The crossover operation does not decrease the diversity of population, and the crossover probability is fixed.
C. Mutation operator: This section employs an adaptive method to adjust mutation probability dynamically based on the ASD value. When the ASD decreasing, mutation probability will be increased to advance the population diversity. The relationship between mutation probability and ASD is given as follows.

where 




where 





2.2.4. Method 4 of ARGA
In this section, a new GA with two species is proposed for the ARGA. The dual-specie GA composes of two sub-populations that constitute of same size individuals. The sub-populations have different characteristics, such as crossover probability and mutation operator. In one sub-population, the parents with higher similarity are cross with higher probability, and mutate with general mutation operator. In the other sub-population, the parents with smaller similarity are cross with higher probability and mutate with big mutation probability. Therefore, the new algorithm can obtain good exploitation and exploration ability [30] .
Multi-population GA [31] - [33] is an extension of traditional single population GA by dividing a population into several isolated sub-populations, within which the evolution proceeds and individuals are allowed to migrate from one sub-population to another [34] , and the flow chart is shown as follows (Figure 1).
Figure 1. The GA of the dual-populations.
For the dual-population GA, one has the following operators:
A. Selection operator: The proposed algorithm establishes two separate sub-populations by random initialization, and then carries on evolution inside single sub-population and migration between two sub-populations. Here, the roulette selection is employed.
B. Crossover operator: The crossover probability is correlated with parents’ similarity. The similarity between two individuals is defined as:


where 










The crossover1 emphasized local search ability, and crossover probability 



C. Mutation operator: Mutation1 is the normal mutation which proceeds with constant probability. Mutation 2 needs to have ability to robustly explore the solution space and to escape from local peak. The probability
of mutation 2 is adaptive mutation probability, and the probability value 




where 



3. Examples
The different four ARGAs will be applied to the BLDC and induction motors. At first, it is needed to show the governing equations of the motor system, and find out what are parameters to be identified.
3.1. Equation of a BLDC Motor
The BLDC motor [35] is one kind of permanent magnet synchronous motor, and has permanent magnets on the rotor and trapezoidal-shape back EMF. The BLDC motor employs a dc power supply switched to the stator phase windings of the motor by power devices, and the switching sequence is determined from the rotor position. The phase current of BLDC motor, in typically rectangular shape, is synchronized with the back EMF to produce constant torque at a constant speed.
A commonly used second-order linear model for a BLDC motor [36] can be expressed mathematically as


where 









3.2. Equation of an Induction Motor
The field-oriented induction motor drive can be applied for high-performance industrial applications, and the controllers implemented in induction motor drives are generally based on the system mathematical model. The parameter identification in a rotation rotor is very useful in monitoring and testing a high-power induction motor drive, and then its performance depends heavily on the motor parameters [37] [38] . In the decoupling condition, main parametric uncertainties of induction motors are the mechanical parameters and load torque disturbances, which are slowly time-varying in general [39] . Measurements of the rotational angular speeds and input electrical voltages are required for the system identification procedure [40] . Model-based methods of rotation-speed estimation are characterized by their simplicity, but sensitivity to parameter variations is considered as the major problem [41] .
The complete electrical and mechanical models [42] are combined, and its electro-mechanical equation can be expressed as follows:

where 
















state variables and the electrical voltages 
4. Numerical Simulation
4.1. For the BLDC Motor
In the numerical simulations, the input voltage is defined as follows:


where






time. In this paper, 







Figure 2. The comparisons of the ARGAs and SRGA. (a) The input voltage; (b) The rotation speed; (c) The errors of rotation speeds between the assigned and identified parameters; (d) The fitness values.
In order to investigate the ARGAs, compare them and find the best one for system identification of the electrical fan, the parameters






From the electrical input voltages and rotation output speed, by using the ARGAs and SRGA the identified parameters and fitness values can be obtained as shown in Table 1. It is seen that the fitness value is largest for method 1 of ARGA, and is smallest for the SRGA. The errors of rotation speeds, which are solved by using the assigned parameters and identified parameters as shown in Table 1, are shown in Figure 2(c). It is seen that the errors of rotation speeds are smaller by the ARGAs than that by the SRGA. The fitness values of the ARGAs and SRGA are compared in Figure 2(d), it is seen that the fitness value of multi-ARGA are not only larger than SRGA, but also the errors of rotation speed are smaller in Figure 2(c).
From comparisons in Figure 2(d), it is demonstrated that the ARGAs are more efficient to identify system’s parameters than the SRGA in generation numbers. It means that the ARGAs do not fall into local optimum and prevent the premature convergence, and the fitness values of ARGAs are bigger than the SRGA. The number simulations are compared,and the fitness value of method 1 of ARGA is 2.54. It is the biggest value than the other ARGAs. Moreover, its error percentages are small not only in parameters but also in the rotation speeds. That means that the method 1 of ARGA is the best algorithm to identify system’s parameters.
4.2. For the Induction Motor
In an induction motor, any vector in a rotating coordinate can be described as follows:

According to Euler’s formula, the three-phase part can be rewritten as:

Therefore, the relation formula can be obtained as follows:
Table 1. The assigned and identified parameters of a BLDC motor by numerical simulations.


The stator transformation formula between the three-phase coordinate and d-q axis is shown as follows:

If there is a voltage amplitude 


The input electrical voltages 

The input voltage is with alternative current (AC) and is shown as Equation (24). If the fixed frequency is defined as



where












In order to investigate the ARGAs for system identification of the electrical fan, the parameters






From the electrical input voltages and rotational output speed, the identified parameters and fitness values by using the ARGAs and SRGA can also be obtained and shown in Table 2. It is seen that the fitness value is the biggest one for method 1 of ARGA, and is the smallest one for the SRGA. The errors of rotation speeds, which are solved by using the assigned parameters and identified parameters as shown in Table 2, are compared in Figure 3(c). It is seen that the errors of rotation speeds are smaller by the ARGAs than that by the SRGA. The


Figure 3. The comparisons of the ARGAs and SRGA. (a) The input voltage; (b) The rotation speed; (c) The errors of rotation speeds between the assigned and identified parameters; (d) The fitness values.
Table 2. The assigned and identified parameters of an induction motor by numerical simulations.
fitness values of the ARGAs and SRGA are compared in Figure 3(d), it is seen that the fitness values of ARGAs are not only larger than the SRGA, but also the errors of rotation speed are smaller in Figure 3(c).
From comparisons in Figure 3(d), it is demonstrated that the ARGAs are more efficient to identify system’s parameters than the SRGA in generation numbers. It means that the ARGAs do not fall into local optimum and prevent the premature convergence, and the fitness values of ARGAs are bigger than the SRGA. The fitness value of method 1 of ARGA is the biggest one in all the ARGAs. Moreover, its error percentages are smaller not only in parameters but also in the rotation speeds. It means that the method 1 of ARGA is the best algorithm among the four ARGAs.
5. Experimental Setup
5.1. For the BLDC Motor
In experiments, the electrical input voltage and rotation output speed of a real motor are to be measured, and the ARGAs are to be employed to obtain system’s parameters. Figure 4 shows the experimental setup, where the computer command is transformed by the driver to a BLDC fan. The input DC voltage and the rotation speed is measured and transformed by the D/A card to computer for the identification computation. The desktop computer edits C language to control microchips, and the inverter will give signal to power supplier, which drives electric fan. At first, the voltage is controlled into the microchips, and the voltage frequency is converted as a sinusoidal function. Secondly, the system is stimulated by the voltage frequency, and the signals of the rotation speeds can be obtained by inverter, and the data is the target to be identify by the ARGAs. At last, the identifiable parameters are substituted into Equations (14) and (15) to obtain the rotation speeds by C language.
5.1.1. Comparisons between the Experimental and Identified Results
In experimental results, three different input voltages are given to the BLDC motor for system’s identification. From numerical simulations, the method1 of ARGA, which not only accurately search for parameters, but also has small generation number inquick convergence, is the best method to identify parameters, and is also applied to the experimental system.
In order to compare experimental results, three different input voltages are employed by hand. The input voltages are ascendant before 1.5 sec and the stable after 1.5 sec, and shown in Figure 5(a) with steady-state voltages: 10.6 V, 11.5 V and 12 V. The rotation speeds for various voltage are comparing in Figure 5(b), where the
Figure 4. Experimental setup.


Figure 5. (a) The input voltages; (b) The comparisons in rotation speeds; (c) The errors of rotation speeds; (d) The convergences of the fitness values for three different input voltages.
curves of the experimental and identified speeds are compared. In Figure 5(b), the identified rotation speeds are approximate with the experimental rotation speeds. The error percentages of rotation speeds are very small when the voltages are stable. The identified and experimental parameters are very approximate. The speed errors of the identified speeds with respect to the experimental ones are shown in Figure 5(c). For the BLDC motor system, the fitness values with respect to total number of generations is shown in Figure 5(d) and all the fitness values converge near the 650th generation.
5.1.2. Comparisons of Identified Parameters
The feasible domains and identified parameters by method1 of ARGA are shown in Table 3. For the three different input voltages, the identified parameters are little different, and the rotation speeds are analogous as show in Figure 5(b). It is noted that the wide feasible domains may affect the identified values of system parameters, and their settings need numerical experience for rapid convergence. It is concluded that the identified parameters will be better if the feasible domains are smaller.
5.2. For the Induction Motor
The electrical input voltages and rotation output speeds of a real induction motor are measured, and the ARGAs are employed to identify system’s parameters in experiments. The experimental setup is shown in Figure 6, where the computer command is transformed by the driver to the induction motor. The input AC voltages and the rotation speeds are measured and transformed by the D/A card to numerical computation. The induction motor is three-phase with the rated specifications: 220 V, 60 Hz, 7 A, and 1720 rpm.
Figure 6. Experimental setup.
Table 3. The identified parameters of a BLDC motor for different input voltages.
5.2.1. Comparisons between the Experimental and Identified Results
The input voltages are given to the induction motor for system’s identification in experimental results. From numerical simulations, the method 1 of ARGA, which not only accurately search for parameters but also has small generation number in quick convergence, is the best method to identify parameters, and is also applied to the experimental identification.
In order to obtain experimental results, 





seen the rotation speeds of the induction motor obtained from LabVIEW are low before 10 sec, and the induction is unstable during this interval. Therefore, the identification is performed after 10 sec when the system is stable. Figure 7(b) compares the curves of the experimental and identified rotation speeds. It is seen that the identified rotation speeds are close to the experimental ones. The comparisons of the identified speeds by the SRGA and ARGA with respect to the experimental ones are shown in Figure 7(c). It is seen that the error per-


Figure 7. (a) The input voltages; (b) The comparisons in rotation speeds; (c) The errors of rotation speeds; (d) The convergences of the fitness values for the SRGA and ARGA.
centages are very small, and the errors of the ARGA are smaller than the SRGA. The fitness value with respect to total number of generations is shown in Figure 7(d). The SRGA converges near the 200th generation. It is seen that the ARGA has faster convergence near the 50th generation and higher fitness value.
In order to validate the identified parameters by the SRGA and ARGA in Equation (16), the input voltage as an exponential function in experiments is taken as follows:

where 


voltages into (16), the rotation speeds are obtained. The rotation speeds for these three voltages are shown in Figures 8(b)-(d), respectively.
The electric currents 


5.2.2. Comparisons of Identified Parameters
The feasible domains and the identified parameters between the SRGA and method 1 of ARGA are compared in Table 4. It is seen the identified parameters are similar in experiments. However, the fitness value of the ARGA


Figure 8. (a) The input voltages; (b) The rotation speeds for 95 V; (c) The rotation speeds for 150 V; (d) The rotation speeds for 210 V.
Table 4. The identified parameters for the SRGA and ARGAs.


Figure 9. (a) The electric current for the input voltage 95 V; (b) The electric current for the input voltage 150 V; (c) The electric current for the input voltage 210 V.
is bigger than the SRGA, and it means the ARGA parameters are more accurate and correct. For the convergence in generations, the ARGA converges at the 53thgeneration, and is faster than the SRGA.
6. Conclusion
This paper attempts to improve crossover and mutation operators in the traditional genetic algorithm by the adaptive technique. Effectiveness of the algorithm in identifying system’s parameters is verified by the BLDC motor and induction motor. It is found that the SRGA and ARGA methods are feasible to system identification. The results show that the ARGA is found to have the faster convergence and the larger fitness value than the SRGA. In numerical simulations, the ARGAs with the identified parameters’ errors percentages are less than 5% with respect to the assigned parameters. In this paper, method 1 of ARGA is found to be the best one to identify parameters of the BLDC and induction motors, and some experimental results are also compared.
Acknowledgements
The financial support from Ministry of Science and Technology of the Republic of China (MOST103-2221- E-327-009-MY3) is gratefully acknowledged.
Cite this paper
Rong-FongFung,Chun-HungLin, (2015) Adaptive Real-Coded Genetic Algorithm for Identifying Motor Systems. Modern Mechanical Engineering,05,69-86. doi: 10.4236/mme.2015.53007
References
- 1. Markovic, M., Hodder, A. and Perriard, Y. (2009) An Analytical Determination of the Torque-Speed and Efficiency-Speed Characteristics of a BLDC Motor. IEEE Conversion Congress and Exposition, September 2009, 168-172.
- 2. Hemati, N. and Leu, M. (1990) A Complete Model Characterization of Brushless DC Motors. IEEE Transactions on Industry Applications, 28, 172-180.
http://dx.doi.org/10.1109/28.120227 - 3. Lee, C.Y. and Hsieh, Y.H. (2012) Bearing Damage Detection of BLDC Motors Based on Current Envelope Analysis. Measurement Science Review, 12, 290-295.
http://dx.doi.org/10.2478/v10048-012-0040-7 - 4. Fazil, M. and Rajagopal, K.R. (2011) Nonlinear Dynamic Modeling of a Single-Phase Permanent-Magnet Brushless DC Motor Using 2-D Static Finite-Element Results. IEEE Transactions on Magnetics, 47, 781-786.
http://dx.doi.org/10.1109/TMAG.2010.2103955 - 5. Wang, S.J., Cheng, C.C., Lin, S.K., Ju, J.J. and Huang, D.R. (2005) An Automatic Pin Identification Method for a Three-Phase DC Brushless Motor. IEEE Transactions on Magnetics, 41, 3916-3918.
http://dx.doi.org/10.1109/TMAG.2005.854970 - 6. Melkote, H. and Khorrami, F. (1999) Nonlinear Adaptive Control of Direct-Drive Brushless DC Motors and Applications to Robotic Manipulators. IEEE/ASME Transactions on Mechatronics, 4, 71-81.
http://dx.doi.org/10.1109/3516.752086 - 7. Wang, W.J. and Wang, C.C. (1998) A New Composite Adaptive Speed Controller for Induction Motor Based on Feedback Linearization. IEEE Transactions on Energy Conversion, 13.
- 8. Krishnan, R. and Doran, F.C. (1987) Study of Parameter Sensitivity in High Performance Inverter Fed Induction Motor Drive System. IEEE Transactions on Industry Applications, IA-23, 623-635.
http://dx.doi.org/10.1109/tia.1987.4504960 - 9. Toliyat, H.A., Levi, E. and Raina, M. (2003) A Review of RFO Induction Motor Parameter Estimation Techniques. IEEE Transactions on Energy Conversion, 18.
http://dx.doi.org/10.1109/TEC.2003.811719 - 10. Wong, C.D., Wang, C.H. and Rung, R.F. (2013) System Identification of an Induction Motor. Chinese Society of Mechanical Engineers in Ilan University.
- 11. Srinivas, M. and Patnaik, L.M. (1994) Adaptive Probabilities of Crossover and Mutation in Genetic Algorithms. IEEE Transactions on System, Man, and Cybernetics, 24, 656-667.
http://dx.doi.org/10.1109/21.286385 - 12. Ginley, B.M., Maher, J., Riordan, C.O. and Morgan, F. (2011) Maintaining Healthy Population Diversity Using Adaptive Crossover, Mutation, and Selection. IEEE Transactions on Evolutionary Computation, 15, 692-714.
http://dx.doi.org/10.1109/TEVC.2010.2046173 - 13. Jiang, Y., Jiang, J. and Zhang, Y. (2011) A Novel Fuzzy Multi-Objective Model Using Adaptive Genetic Algorithm Based on Cloud Theory for Service Restoration of Shipboard Power Systems. IEEE Transactions on Power Systems, 27, 612-620.
http://dx.doi.org/10.1109/TPWRS.2011.2179951 - 14. Schaible, U. and Szabados, B. (1999) Dynamic Motor Parameter Identification for High Speed Flux Weakening Operation of Brushless Permanent Magnet Synchronous Machines. IEEE Transactions on Energy Conversion, 14, 486-492.
http://dx.doi.org/10.1109/60.790901 - 15. Goldberg, D.E. and Holland, J.H. (1988) Genetic Algorithms and Machine Learning. Machine Learning, 3, 95-99.
- 16. Ha, J.L., Fung, R.F. and Han, C.F. (2005) Optimization of an Impact Drive Mechanism Based on Real-Coded Genetic Algorithm. Sensors and Actuators A: Physical, 121, 488-493.
http://dx.doi.org/10.1016/j.sna.2005.03.001 - 17. Chang, P.C., Hsieh, J.C. and Wang, C.Y. (2007) Adaptive Multi-Objective Genetic Algorithms for Scheduling of Drilling Operation in Printed Circuit Board Industry. Applied Soft Computing, 7, 800-806.
http://dx.doi.org/10.1016/j.asoc.2006.02.002 - 18. Raman, S. and Patnaik, L.M. (1996) Performance-Driven MCM Partitioning through an Adaptive Genetic Algorithm. IEEE Transactions on Very Large Scale Integration Systems, 4, 434-444.
http://dx.doi.org/10.1109/92.544408 - 19. Wang, F., Li, J., Liu, S., Zhao, X., Zhang, D. and Tian, Y. (2014) An Improved Adaptive Genetic Algorithm for Image Segmentation and Vision Alignment Used in Microelectronic Bonding. IEEE/ASME Transactions on Mechatronics, 19, 291-296.
http://dx.doi.org/10.1109/TMECH.2013.2260555 - 20. Wang, L. and Tang, D.B. (2011) An Improved Adaptive Genetic Algorithm Based on Hormone Modulation Mechanism for Job-Shop Scheduling Problem. ELSEVIER Expert Systems with Applications, 38, 7243-7250.
http://dx.doi.org/10.1016/j.eswa.2010.12.027 - 21. Yuan, L.Z., Xiao, B. and Wei, X.J. (2010) BP Network Model Optimized by Adaptive Genetic Algorithms and the Application on Quality Evaluation for Class Teaching. IEEE International Conference on Future Computer and Communication, 3, 273-276.
http://dx.doi.org/10.1109/icfcc.2010.5497635 - 22. Du, Y., Fang, J. and Miao, C. (2014) Frequency-Domain System Identification of an Unmanned Helicopter Based on an Adaptive Genetic Algorithm. IEEE Transactions on Industrial Electronics, 61, 870-881.
http://dx.doi.org/10.1109/TIE.2013.2257135 - 23. Yang, X. (2012) Quantitative Detection for Gas Mixtures Based on the Adaptive Genetic Algorithm and BP Network. Proceedings of the IEEE International Conference on Industrial Control and Electronics Engineering, Xi’an, 23-25 August 2012, 1341-1344.
- 24. Lin, G. and Liu, G. (2010) Tuning PID Controller Using Adaptive Genetic Algorithms. Proceedings of the IEEE International Conference on Computer Science and Education, Hefei, 24-27 August 2010, 519-523.
http://dx.doi.org/10.1109/iccse.2010.5593559 - 25. Chang, C.Y. and Chen, D.R. (2010) Active Noise Cancellation without Secondary Path Identification by Using an Adaptive Genetic Algorithm. IEEE Transactions on Instrumentation and Measurement, 59, 2315-2327.
http://dx.doi.org/10.1109/TIM.2009.2036410 - 26. Xu, X.Q. and Lei, L. (2011) The Research of Advances in Adaptive Genetic Algorithm. Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, 14-16 September 2011, 1-6.
- 27. Lin, C. (2009) An Adaptive Genetic Algorithm based on Population Diversity strategy. Proceedings of the 3rd International Conference on Genetic and Evolutionary Computing, Guilin, 14-17 October 2009, 93-96.
http://dx.doi.org/10.1109/wgec.2009.67 - 28. Potts, J.C. and Giddens, T.D. (1994) The Development and Evaluation of an Improved Genetic Algorithm Based on Migration and Artificial Selection. IEEE Transactions on Systems, Man, and Cybernetics, 24, 73-86.
http://dx.doi.org/10.1109/21.259687 - 29. Li, T.H., Lucasius, C.B. and Katerman, G. (1992) Optimization of Calibration Data with the Dynamic Genetic Algorithm. Analytica Chimica Acta, 268, 123-134.
http://dx.doi.org/10.1016/0003-2670(92)85255-5 - 30. Li, J.H. and Li, M. (2008) Genetic Algorithm with Dual Species. Proceedings of the IEEE International Conference on Automation and Logistics, Qingdao, 1-3 September 2008, 2572-2575.
http://dx.doi.org/10.1109/ical.2008.4636604 - 31. Nowostawski, M. and Poli, R. (1999) Parallel Genetic Algorithm Taxonomy. Proceedings of the IEEE International Conference on Knowledge-Based Intelligent Information Engineering Systems, Adelaide, 31 August-1 September 1999, 88-92.
http://dx.doi.org/10.1109/kes.1999.820127 - 32. Alba, E. and Tomassini, M. (2002) Parallelism and Evolutionary Algorithms. IEEE Transactions on Evolutionary Computation, 6, 443-462.
http://dx.doi.org/10.1109/TEVC.2002.800880 - 33. Chen, F., Jiang, B., Tao, G. and Zhang, X. (2013) Improved Adaptive Genetic Algorithm For Grid Resource Scheduling via Quantum Control Techniques. Proceedings of the IEEE Control and Decision Conference, Guiyang, 25-27 May 2013, 3974-3978.
http://dx.doi.org/10.1109/ccdc.2013.6561644 - 34. Jiang, Y., Jiang, J. and Zhang, Y. (2012) A Novel Fuzzy Multi-Objective Model Using Adaptive Genetic Algorithm Based on Cloud Theory for Service Restoration of Shipboard Power Systems. IEEE Transactions on Power Systems, 27, 612-620.
http://dx.doi.org/10.1109/TPWRS.2011.2179951 - 35. Shao, J., Nolan, D., Teissier, M. and Swanson, D. (2003) A Novel Microcontroller-Based Sensorless Brushless DC (BLDC) Motor Drive for Automotive Fuel Pumps. IEEE Transactions on Industry Applications, 39, 1734-1740.
- 36. Kuria, J. and Hwang, P. (2011) Investigation of Thermal Performance of Electric Vehicle BLDC Motor. International Journal of Mechanical Engineering, 1, 1-17.
- 37. Liaw, C.M., Chao, K.H. and Lin, F.J. (1992) A Discrete Adaptive Field-Oriented Induction Motor Drive. IEEE Transactions on Power Electronics, 7, 411-419.
- 38. Attaianese, C., Damiano, A., Gatto, G., Marongiu, I. and Perfetto, A. (1998) Induction Motor Drive Parameters Identification. Transactions on Power Electronics, 13.
- 39. Wang, W.J. and Wang, C.C. (1999) Speed and Efficiency Control of an Induction Motor with Input-Output Linearization. IEEE Transactions on Energy Conversion, 14, 373-378.
- 40. Shaw, S.R. and Leeb, S.B. (1999) Identification of Induction Motor Parameters from Transient Stator Current Measurements. IEEE Transactions on Industrial Electronics, 46, 139-149.
http://dx.doi.org/10.1109/41.744405 - 41. Zaky, M.S., Khater, M.M., Shokralla, S.S. and Yasin, H.A. (2009) Wide-Speed-Range Estimation with Online Parameter Identification Schemes of Sensorless Induction Motor Drives. IEEE Transactions on Industrial Electronics, 56, 1699-1707.
http://dx.doi.org/10.1109/TIE.2008.2009519 - 42. Liaw, C.M., Kung, Y.S. and Wu, C.M. (1991) Design and Implementation of a High-Performance Field-Oriented Induction Motor Drive. IEEE Transactions on Industrial Electronics, 38, 275-282.
NOTES
*Corresponding author.

















