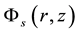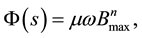Modern Mechanical Engineering
Vol.04 No.02(2014), Article ID:45839,23 pages
10.4236/mme.2014.42009
Heat Flux Analysis in Electrical Transformers through Integral Operators of Mechanics
Francisco Bulnes1, Alejandro R. Tello2, Máximo Livera3
1Research Department of Mathematics and Engineering, TESCHA, Federal Highway Mexico-Cuautla “La Candelaria”, Chalco, Mexico
2Headquarters of Computational Systems Engineering, TESCHA, Federal Highway Mexico-Cuautla “La Candelaria”, Chalco, Mexico
3Federal Highway Mexico-Cuautla “La Candelaria”, Chalco, Mexico
Email: francisco.bulnes@tesch.edu.mx, atello1@yahoo.com, Maximo@Gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 February 2014; revised 3 April 2014; accepted 16 April 2014
ABSTRACT
Considering the continuous functioning of a power transformer under charge of high capacity of 50 MVA, predicted studies are proposed to be performed of their thermal behavior under perma- nent and variable regimens of flow of charge, using non-invasive methods based in integral trans- forms that measure and determine parameters of geometrical, analytical and physical type of the transformer. In before works, we have studied a basic geometry of a winding composed of high and low voltage sections with a uniform heat generation and heat convection boundary conditions. The heat conduction equation representing the phenomena of heat generation in a cylindrical structure was solved by using an integral transform. In this sense, this new study considers the basic geometry composed of a three cylindrical windings (high and low voltage turns) and a rec- tangular core. Thus it is proposed to solve magnetic flow equations using integral transforms (Han- kel transforms and Bessel integrals) in order to obtain the heat source distribution in the core due to the magnetization currents which are developed in function of the magnetic field flow equations. Based on this, it is proposed as a second step to use this heat source distribution to obtain the corresponding temperature distribution in the core by solving the cylindrical heat conduction equation for the core (cylindrical). Bearing this in mind, it is proposed finally to solve the 3D cylindrical heat conduction equation for the one winding using the calculated heat convection coefficients, the conductivity of the winding, behavior of the mineral oil and the non uniform winding heat generation predicted in recent researches. This equation will be solved by using integral methods (Radon, Hankel and Fourier transforms). This methodology will be useful to establish a new design of a power transformer based on the values of their integrals and the results that throw the inverse methods for this case. Finally if possible we will use the programs of Fluent and/or Phoenics for the validation of functional proposed models of prediction and prevention of heat flow and charge based on the obtained results.
Keywords:
Power Transformer, Thermal Model, Critical Temperature Points, Integral Transforms to Heat Flux, Magnetic Flux

1. Introduction
Power transformers are devices which are used to convert the electrical energy from a high voltage level to a lower voltage level that can be distributed among domestic and industrial users. These levels vary in the 13 to 34.5 kV high level voltage to 220 to 480 V lower level voltage [1] .
Nowadays various power transformers designs can be found in the industry which can be differentiated on the basis of the inclusion of new core materials or the type of cooling system. In this respect, manufacturers continue to analyze the thermal design of the cooling ducts for the assembly of windings-core as well as the cooling efficiency of the radiators of the transformer. A characteristic transformer geometry is depicted in Figure 1.
IEEE standards [2] do not mention calculation of detailed oil temperature distributions neither the best fan arrangements in order to achieve the highest thermal efficiency. Nevertheless, the cited IEEE standards [2] do mention how to calculate the oil temperature rises and winding temperature rises using empirical formulas. Some transformer manufacturers refer to methods of calculation which are based on the fundamental theory of heat transfer in order to calculate the oil and winding temperature rises. Recently, researchers [3] have focused on the detailed calculation of oil and windings temperature distributions of the transformer. This method is aimed to determine the maximum windings temperature (hot spot). Then, researchers have taken different ways of calculation of the detailed oil and windings temperatures such as concentrated parameters, thermal-hydraulic net, numerical and analytical techniques [4] -[8] .
From this outset, it can be deduced that the detailed thermal calculation of electric transformers is required and herein the computational thermal model as well as the functional analysis based on the energy optimization of the transformer is used to obtain the detailed oil and winding temperatures.
2. Functional Analysis
The functional analysis is based on the solution of a fundamental equation derived from fundamental theory

Figure 1. Transformer winding. (a) Side view; (b) Top view.
which is composed of a defined integral over the  space and values in
space and values in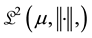 . This equation is a first order integral equation which propose solutions for the transformer through cylindrical functions that model more precisely the cooling effects that are considered [9] [10] .
. This equation is a first order integral equation which propose solutions for the transformer through cylindrical functions that model more precisely the cooling effects that are considered [9] [10] .
The referred cylindrical functions are Bessel type, first order. The proposed model will embody harmonic regular solutions defined in a finite interval, which is an immediate consequence of the use of an integral transform method, which is applicable to a decreasing function defined in the cylindrical radius. Regularity of obtained solutions and the spectral analysis of the points of continuous perturbation (heating points of the transformer core or temperature singular points) are considered through the integral transform such as the Hilbert transform, obtaining the real and imaginary parts of the impedance of the load of the transformer core, which is partly responsible of the heating.
It is worth to mention that bay using perturbation theory, the perturbation space has an spectrum in a w-space of hyperbolic type, being necessary the asymptotic developments of the matrix coefficients for the functional equation that models our phenomena in the approach and analysis of the phenomena which in turn determine the ergodicity for the complete set of parameters which are necessary for a precise analysis of the heat flux and representatively in heat control instruments that measure energies in 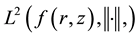 [10] .
[10] .
On the other hand, identification of the heating points within the physical interior space of the transformer is important for the location of the heating source and its likely cause, being applicable a vector tomography of the core and windings, obtaining in this way an exact image of the heat flux, the velocity currents of cooling and the geometry of the temperature states in the inner core and windings.
Nevertheless, within the electromagnetic design of a transformer, it is evident that locating and identifying those heating points, as well as the heat distribution in the inner core and windings is necessary in the redesign of the cooling systems which have to be applied to the precisely located heating zones.
3. Integral Transform of Heat Transfer in Electrical Transformers
Considering Maxwell equations, in reference to the existence of magnetic flux 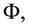 parallel to boundary [11],
parallel to boundary [11],
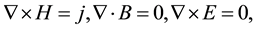 (1)
(1)
These are equivalent to Laplace equations with magnetic flux 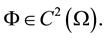 Then performing a cylindrical transformation of Laplacian, yields
Then performing a cylindrical transformation of Laplacian, yields
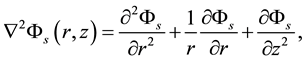 (2)
(2)
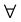 magnetic potential (it is the component of potential of the magnetic vector at the boundary)
magnetic potential (it is the component of potential of the magnetic vector at the boundary) 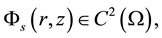 under the boundary conditions:
under the boundary conditions:
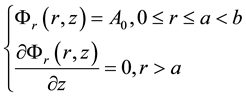 (3)
(3)
Referring to Equation (1), 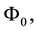 is the magnetic potential of the transformer cylindrical core, as it is shown in Figure 1. Real geometry of transformer is shown in Figure 2. If we consider temperature as function
is the magnetic potential of the transformer cylindrical core, as it is shown in Figure 1. Real geometry of transformer is shown in Figure 2. If we consider temperature as function 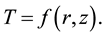 Then function
Then function 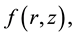 must be a function stemming from spectral transform of
must be a function stemming from spectral transform of 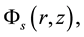 on a symmetric space. The core that is analyzed is symmetrical due to the fact that is a straight circular cylinder composed of disks of radius
on a symmetric space. The core that is analyzed is symmetrical due to the fact that is a straight circular cylinder composed of disks of radius 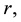 and height
and height 
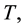

such that we apply the Hankel transform to the Laplace equation, yielding:

Solutions of this differential equation are:

Figure 2. Core ground and their high voltage conductors.
where

Reformulating our boundary conditions for the temperature function 



and the corresponding conditions in 


Using boundary conditions (7), in solutions given in (6), yields:

Performing similarly for boundary conditions in (7), yields

Finally and applying Inverse Hankel transform to the superposition of solutions proposed for the geometry of space interactions 

The tangent vector spectrum is derived from the pre-defined boundary conditions by the derivatives:

From which differential Equation (5) is obtained, for any segment

then

which demonstrate the consistency of our procedure over any segment
4. Specific Generation of Heat in Winding and Analytical Solution of Heat Transfer Equation
The geometry considered for the transformer is the one for a three phase power transformer of 30 MVA capacity which is simplified to a two dimension cylindrical winding model which in turn is composed of high and low voltage windings and a central portion of core. Such geometry is shown in Figure 3.

Figure 3. (a) Heat measure per unit of sectional conductor; (b) Total contribution of the generated heat for all electrical conductors.
It is being considered a simplified geometry of the core of the transformer with an inner ring of radius 

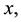
The abovementioned winding has a generation of heat coming from the high and low voltage windings. It is not considered the heat produced by the core. For the analysis it was determined that the cylindrical coordinates heat transfer equation would be considered:

The solution of the equation shown is performed considering the boundary conditions (8):


the solution of (15) is given by (11).
As a special case it is considered heat conduction through our cylinder under a heat rate given by 

where

If 










The integral transform is being deduced from the Green function as a core of an integral transform better known as Green transform [9] , within the chosen winding. The corresponding functions are spectral functions of heat and the integral (19), is the Green operator which determines the temperature distribution in points of the conductor (see Figure 2, Figure 3(a) and Figure 3(b), Figures 4-6).
5. Computational Model for Integral Transforms of Thermo-Magnetism
Considering ideally the horizontal problem [13] [14] , in other words, over the horizontal outward appearance




Describing this problem through the integral equation:

where
Figure 4. Potential surface of temperature.
Figure 5. Heat flow generated by one conductor section. The Bessel function is: J = besselh (0, 2, x + i*y).
Figure 6. Irradiated heat diffusion curve for winding x.
where







parametric representation of a smooth contour



that 


function, 


From the complex integral Equation (20), we pass to a system of real equations, assuming:



Figure 7. (a) Heat flow from magnetic potentials 




Approaching the functions






The indeterminate coefficients










of this work. Then the system of Equations (21)-(23), can be represented in a finite form by means of the vector equation:

where the components of the vector equations are:


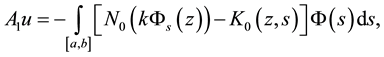


The operator




In the continuum media of high viscosity such as the oil used inside of the transformer, the heat that from the magnetic field is comported and shaped by the magnetic lines which are closed [2] [5] . This shapes a solid of certain symmetries consigned from the symmetry of magnetic field (see the Figure 8, [15] -[17] ).
6. Distribution of Temperature According to the Variation of Output
Let’s consider an alternative solution to the heat equation for the high-low voltage of a power transformer according to the variation of response to a variation in voltage as input to the power system. After, we will obtain a model of thermal diffusion derived from the inverted energy by the winding to move the potential in the two voltages ranges, the high voltage range 13 - 34.5 kV and the low voltage range 220 - 480 V as was described in the introduction.
Considering the diffusion of heat bay means of the energy equation applied to the heat generation

This problem will be addressed later in future work following the solution given [2] , where temperature only varies with coordinate

Figure 8. 3-D Thermal model of oil flow and their evolution inside the transformer core. The MathLab routine is given by multi-physics design ande modeling using the conditions: yy = yy.*cos(order*phi); order = max(max(abs(yy))); rho = 5 + 2 *yy/order; r = rho. *sin(theta); x = r. *cos(phi); y = r. *sin(phi); z = rho.*cos(theta); clf >> surf(x,y,z).

Taking the Hankel transform of the first term:

Evaluating the last term of the above equation:

Then

Considering the boundary conditions:

From which:

and

Then:

Then expanding the first and second term, we have:

and considering

For the second term of the differential equation we have

Using (43) and (44), we have
Applying the finite Fourier transform we found:

Again, expanding the first two terms:
Considering the boundary conditions:

And

Then

Now substituting

The third term is:
Then:

Applying the Fourier transform to the rest of the differential equation and including the results previously obtained:

which yields

or

where

7. Results
In this study the following physical considerations were considered while developing the numerical simulations. Taking into account these real parameters the thermal model is completely simulated as a system, following the technical specifications being considered in the electrical industry [2] -[6] [11] -[14] .
Data considered for the analysis were given by the Table 1.
In the case of a distribution transformer a symmetrical section was considered along the vertical axis of the transformer, according to the geometrical dimensions and shape of the assembly windings-core. The average conductivity of the windings-core was 8.94 W/m・˚C.
In reference to Figure 9, the reduction in oil temperature is observed in the lower part of the transformer. This is due to the cooling effect that is taking place in the radiator. The simulation was performed using FLUENT™ [3] [13] .
In reference to the numerical results for the power transformer model of 30 MVA, the corresponding data for a disk are shown in Table 2.
According to the data shown on Table 2 a solution was obtained by using Matlab (see the Figure 10).
Figure 9. Temperature distribution due to the heat generation coming from windings-core.
Table 1. Transformer and cooling media data.
Figure 10. Winding temperature distribution, Tamb = 30˚C, Re = 750, ht = 0.08 W/m2 ˚C, hb = 0.03 W/m2・˚C. The red top of the surface corresponds to the temperature that provokes the 2-surface using to the model in this direction.
Table 2. Power transformer data.
Then a numerical simulation using Comsol was performed in an air cooled transformer. The experiment includes a transient simulation of the electromagnetic effect created by the B-H curve for the core which produces the electrical and magnetic distribution. Data for the simulation is shown in Table 3. The resulting electrical currents are shown in Figure 11.
We realize the analysis of some functions that are characteristics of the thermal-magnetic behavior (see Figure 12(a) and Figure 12(b), Table 3 and Table 4):
Figure 11. Winding electrical currents.
Table 3. Data on electrical design characteristics of the transformer for the simulation.
Table 4. Material parameters.
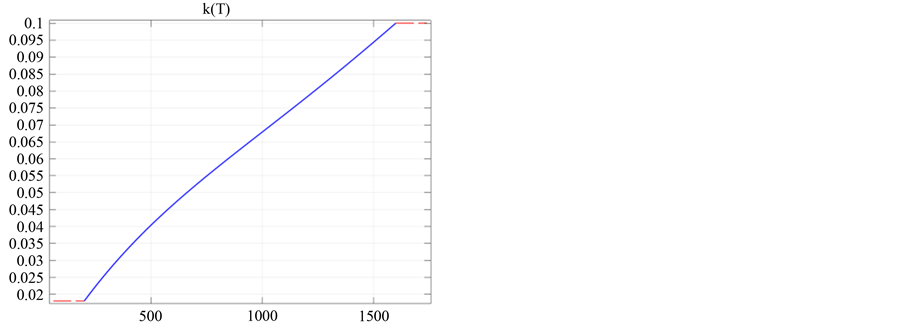

Figure 12. Functions of (a) heating capacity to constant pressure



The corresponding energy equation considered for the analysis was:

The geometry used as well as the corresponding surface magnetic flux density and air flow distribution is shown in Figures 13-15.
Considering the solution presented in Section 4, additional results are presented (see the Figure 16(a) and Figure 16(b)):
To obtain the idealized states of winding temperature distributions showed in the Figure 16(a) and Figure 16(b), is necessary that let designed an distribution of heat on the geometrical entire of the transformer core obeyed the cylindrical geometry and heat source produced inside the transformer core. Very of this heat is produced in the centre the core and generated by the winding through the contribution of each conductor line around of nucleus. The contribution of the magnetic field (which produced heat) in this idealized case can be given by our Hankel transform as shows the Figure 17. The cooling is idealized with the optimal cooling system

Conjecture. (F. Bulnes-A. Tello). The degeneration of the hyperbolic space of heat flow inside the transformer (perturbation singular space) must be to an elliptic space with one finite singularity bounded by the Fourier coefficients given in (53) (see the Figure 18).
The elliptic space is more stable than the hyperbolic space. Their solutions can be approximated by harmonics terms that fluctuate inside the amplitudes space to Fourier series (see Figure 19). The hyperbolicity of the heat
Figure 13. Transformer geometry.
Figure 14. Surface magnetic flux density.
Figure 15. Air flow velocity distribution.
flow space, as is said, depends of the magnetic field and their potentials. Then we want become this hyperbolicity in an elliptic behavior of our electromagnetic solutions to derive an elliptic behavior in our magnetic field solutions and we obtain stability (uniformity of heat increasing and bound to this heat) (see the Figure 20 and Figure 21).

Figure 16. Idealized winding temperature distributions shaped by the specific heat and heating capacity to constant pressure curve (see the Figure 12(a) and Figure 12(c)).
Figure 17. Idealized cooling of the transformer nucleus.

Figure 18. Hyperbolic and elliptic heat flow behavior.
8. Conclusions
The development of solution to the conduction heat equation represents a physical phenomenon that includes natural convection of a fluid in power transformers. Several approaches were presented including analytical using the Hankel transform and numerical schemes.
The numerical solutions using Fluent were presented as well as Comsol Multiphysics. In the first case of the analytical solution a 30 MVA ONAN power transformer was considered. For the numerical solutions an air cooled
Figure 19. Thermo magnetic wave from the heat term
Figure 20. From (55) taking the inputs

e-transformer was simulated having a one turn relation and a resistance connected to the primary and secondary sides and air convection. Also, the thermal simulation of a distribution transformer was presented.
According to the graphs shown it is interesting to note that several data which are quite helpful to the designer are obtained. The effects of different thermal parameters are shown and a maximum winding temperature is observed. IEEE standard [2] presents a way of calculating the maximum winding temperature based on a methodology. This standard does not include the location of the hot spot. This hot spot can be located based on the numerical and analytical approaches. Other authors have developed similar solutions of the heat conduction equation regarding location of hot spot and their numerical value. Values and location of hot spot encountered by these authors are dependent on the type of method of solution and vary according to the construction of the

Figure 21. (a) Global: current in secondary winding; (b) Global: current in primary winding.
transformer. Results there shown are in concordance to the ones found in this work in respect to the approaches used in this work to obtain the maximum winding temperature.
Acknowledgements
Authors thank the encouragement given by Technological Institute of High Studies of Chalco, for development of these works and financial support.
References
- Pierce, L.W. and Holifield, T. (1999) A Thermal Model for Optimized Distribution and Small Power Transformer Design. IEEE Transactions on Power Systems, 2, 925-929.
- (1996) ANSI/IEEE Loading Guide for Mineral oil Immersed Transformer. C57.91-1995.
- Tello, A. (2009) Modelo Térmico de Transformador Eléctrico. Tesis de Doctorado, Escuela Superior de Ingeniería Mecánica (ESIME), Instituto Politécnico Nacional, Ciudad de México.
- Susa, D., Lethonen, M. and Nordman, H. (2005) Dynamic Thermal Modeling of Power Transformers. IEEE Transactions on Power Delivery, 20, 197-204. http://dx.doi.org/10.1109/TPWRD.2004.835255
- Nordman, H. (2004) Average Oil Temperature Rise in Distribution Transformers without External Oil Circulation. Te- chnical Memorandum, 2004-03-15.
- Montsinger, V.M. (1951) Thermal Characteristics of Transformer. In: Blume, L.F., et al., Eds., Transformers Engineering: A Treatise on the Theory, Operation and Application of Transformers, Wiley, New York.
- Pradhan, M.K. and Ramu, T.S. (2003) Prediction of Hottest Spot Temperature (HST) in Power and Station Transformers. IEEE Transactions Power Delivery, 18, 1275-1283. http://dx.doi.org/10.1109/TPWRD.2003.817739
- (2005) Market and Technology Assessment. Prentice Hall, Upper Saddle River.
- Bulnes, F. (1998) Treatise of Advanced Mathematics: Analysis of Signals and Systems. Faculty of Science, National Autonomous University of Mexico, Mexico City.
- Bulnes, F. (2008) Analysis of Prospective and Development of Effective Technologies through Integral Synergic Operators of the Mechanics. In: 14th Scientific Convention of Engineering and Arquitecture: Proceedings of the 5th Cuban Congress of Mechanical Engineering, ISPJAE and Superior Education Ministry of Cuba, Eds., 2-5 December 2008, Havana.
- Feynman, R., Leighton, R. and Sands, M. (1964) Electromagnetism and Matter. Addison-Wesley, Boston.
- Bulnes, F. and Maya, J. (2009) Synergic Integral Operators and Thompson Effect to the Evaluating to Temperature Electrical Conductors. CIM2009, Electrical Engineering, Instituto Tecnológico de Orizaba, Veracruz, 328-335.
- Bulnes, F. and Tello, A. (2010) Thermal Modeled of Electric Transformers through Their Evaluating by Integral Operators of the Mechanics (II). Proc. 15ª CCIA-SIDEGI, CUJAE, Ministerio de Educación Superior de Cuba, Habana, 273-279.
- Pierce, L.W. (1994) Hottest Spot Temperatures in Ventilated Dry Type Transformers. IEEE Transactions on Power Delivery, 9, 257-264. http://dx.doi.org/10.1109/61.277697
- Alegi, G.L. and Black, W.Z. (1990) Real Time Thermal Model for an Oil-Immersed Forced Air Power Transformer. IEEE Transactions on Power Delivery, 5, 991-999. http://dx.doi.org/10.1109/61.53112
- Ramaswamy, B. and Jue, T.C. (1992) Some Recent Trends and Development in Finite Element Analysis for Incompressible Flows. International Journal for Numerical Methods in Engineering, 35, 671-707. http://dx.doi.org/10.1002/nme.1620350405
- Patankar, S.V. (1980) Numerical Heat Transfer and Fluid Flow. Hemisphere, New York.
Appendix A
Theorem (F. Bulnes, A. Tello) A. 1. From a point of view of heat transfer an electrical transformer is a box 





Proof. Let



where the state manifold
zontal spaces (as elements corresponding horizontal bundle

where



Then the manifold

the heat flow) we have a smooth map 



where the 1-form 


1Thermo-dynamical manifold of points 




2By the conservation of energy for a closed system as 
3These maps characterize this sub-manifold with Riemannian structure. The idea of the smooth map
4Hankel functions with the functional integral expressions:
which have spectral solutions given by (4), where explicitly their solutions are functions
By (4) the unique functions that shape the horizontal bundles are created to start of the magnetic field. But these come from of the geometry of the core of transformer. These functions are 





which in particular are the spherical functions 
These functions are radial and shape the vertical bundles in the z-direction. Then the smooth map



But the Equation (60) can be write through the temperature measured by the

Using (A.6) (A.7) and the modeling given by the Section 5, we have to all bundle

An approximation in their extending to a Hilbert space








where

where
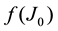

The demonstration of (A.9) can be obtained using the fact that (53) haves the form

where 


which proves (A.8). Then their trace is the temperature
Here the extension, the operator


Technical Notation
5Consider the spherical function:













6
7