Modern Mechanical Engineering
Vol.3 No.1(2013), Article ID:28252,7 pages DOI:10.4236/mme.2013.31003
Study on Interface Friction Model for Engineering Materials Testing on Split Hopkinson Pressure Bar Tests
1Key Laboratory of Testing Technology for Manufacturing Process (Ministry of Education), Southwest University of Science and Technology, Mianyang, China
2Student Office of School of Arts and Literature, Southwest University of Science and Technology, Mianyang, China
Email: *yubinluzju@hotmail.com, songshupanda@hotmail.com
Received November 15, 2012; revised December 20, 2012; accepted December 31, 2012
Keywords: Kinetic Interface Friction Model; Sliding Velocity; Contact; Split Hopkinson Pressure Bar (SHPB); Engineering Materials
ABSTRACT
Split Hopkinson pressure bar (SHPB) has become a frequently used technique to measure the uniaxial compressive stress-strain relation of various engineering materials at high strain-rates. The accuracy of an SHPB test is based on the assumption of uniaxial and uniform stress distribution within the specimen, which, however, is not always satisfied in an actual SHPB test due to the existence of some unavoidable negative factors, e.g., interface friction constrains. Kinetic interface friction tests based on a simple device for engineering materials testing on SHPB tests are performed. A kinetic interface friction model is proposed and validated by implementing it into a numerical model. It shows that the proposed simple device is sufficient to obtain kinetic interface friction results for common SHPB tests. The kinetic friction model should be used instead of the frequently used constant friction model for more accurate numerical simulation of SHPB tests.
1. Introduction
Split Hopkinson pressure bar (SHPB) technique, as shown in Figure 1, is commonly used to determine the strain-rate dependence of the dynamic compressive properties for engineering materials such as metals, concrete-like materials and polymers. Due to the significant importance and great success of SHPB in the dynamic testing of mechanical properties of engineering materials, SHPB has been named by American Society of Mechanical Engineers (ASME) as a historical engineering landmark [1]. It was estimated from the most comprehensive engineering science database, Engineering Village, that more than 2500 papers have been published on SHPB related researches since 1949. It was shown by both Engineering Village and Science Citation Index that the number of publications on SHPB has increased dramatically since 1980s, as shown in Figure 2. But it is expected that a valid SHPB test should give the uniaxial stress-strain curve at the planned strain-rate, which im-

Figure 1. The schematic of SHPB technique.
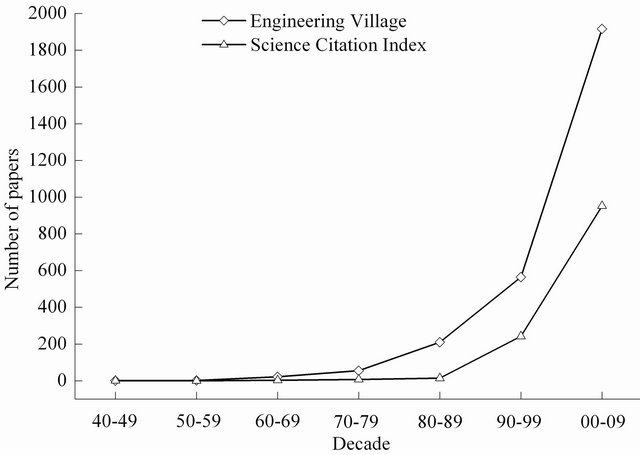
Figure 2. Estimation of the total number of papers published in each decade between 1940 and 2009 where an SHPB test was used to obtain the high strain-rate mechanical properties of materials.
poses requirements of uniaxial and uniform stress distribution in the SHPB specimen while the strain-rate variations in the specimen during the effective range of an SHPB test are small. However, these requirements are not satisfied in some SHPB tests, and therefore, the strain-rate effects due to the non-strain-rate factors cannot be considered as genuine strain-rate effects in an SHPB test.
Friction between specimens and anvils has long been recognized as a problem in compression testing, both at low [2] and high strain-rates of deformation [3,4]. It has three major effects, i.e., 1) it generates a shear stress at the specimen/anvil interface and so changes the stress state in the specimen from uniaxial to triaxial [5] which leads to the measured stress being higher than the true strength (yield stress) of the material [6]; 2) the specimen does not preserve its original geometry but ‘barrels’ [5,7-10]; 3) localization of deformation within the specimen is promoted due to frictional locking of the surface resulting in truncated cones of non-deforming material which slide over the unconstrained material at the sides [5,11,12]. These shear bands are often precursors of fracture [13]. Accordingly, interfacial friction constrains between SHPB specimen and pressure bars are one of the non-strain-rate factors that may significantly affect the SHPB results by violating the uniaxial stress state through boundary constrains [3,14-19].
Thus, constructing a proper interface friction model is vital for the accurate determination of material properties. Over the years two main methods have been developed for the study of friction relevant to compression testing, i.e., 1) the ring test, e.g. [2,3] and 2) the aspect ratio test where cylinders with a variety of different height/diameter ratios are used. Of the two, probably the ring test is the most used with at least 160 published studies. The Avitzur analysis [20-26] has been checked using highspeed photography [27-29]. In this study, kinetic friction coefficients for various engineering materials sliding against stainless steel measured from a simple slip-way setup are presented, and a kinetic interface friction model for engineering materials testing on SHPB tests is proposed in Section 1. The kinetic friction model is used to interpret and correct the compression stress-strain curves obtained from SHPB tests in Section 2 followed by discussion in Section 3. Conclusions are drawn in Section 4.
2. A Kinetic Interface Friction Model in SHPB Tests
The Coulomb friction model is widely used in numerical simulations of contact problems
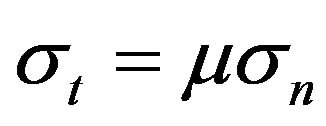 (1)
(1)
in which  is the tangential friction force per unit area,
is the tangential friction force per unit area, 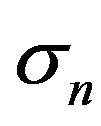 is the pressure in normal direction of the contact area, and
is the pressure in normal direction of the contact area, and  is the coefficient of friction, which has been taken as a constant in many previous numerical simulations of SHPB tests (e.g. [14,19]). Researchers like Siebel [30], Briscoe and Nosker [31], Malinowski and Klepaczko [15] and Wang et al. [32] have also proposed theoretic expressions for the influence of the interface friction on the dynamic compressive behavior of engineering materials in SHPB tests. However, they also used a constant friction coefficient.
is the coefficient of friction, which has been taken as a constant in many previous numerical simulations of SHPB tests (e.g. [14,19]). Researchers like Siebel [30], Briscoe and Nosker [31], Malinowski and Klepaczko [15] and Wang et al. [32] have also proposed theoretic expressions for the influence of the interface friction on the dynamic compressive behavior of engineering materials in SHPB tests. However, they also used a constant friction coefficient.
In fact, in an SHPB test, the relative velocity (sliding velocity) between the end surfaces of the SHPB specimen and the pressure bars varies continuously at different time and different position of the surface, which causes the variation of the friction coefficient since it is dependent of the relative velocity between two contacting surfaces. The kinetic friction coefficient is normally smaller than the static friction coefficient (for some macromolecular materials, e.g. Polyurethane, their kinetic friction coefficient is larger than the static one [33], which will not be studied in this paper). In an SHPB test, when assuming the specimen to be incompressible, the maximum relative radial velocity on the interfaces between the SHPB specimen and the end surfaces of the pressure bars can be estimated by [34]
 (2)
(2)
in which 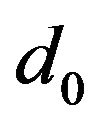 is the original outer diameter of the specimen,
is the original outer diameter of the specimen, 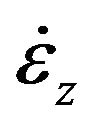 is the engineering axial strain-rate and
is the engineering axial strain-rate and  is the engineering axial strain. Thus, for a mortar specimen of
is the engineering axial strain. Thus, for a mortar specimen of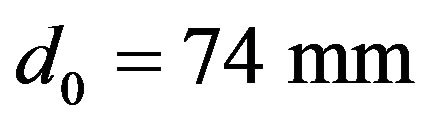 , Figure 3 shows the variation of the maximum relative radial velocity (
, Figure 3 shows the variation of the maximum relative radial velocity (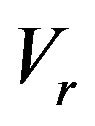 , at the edge of specimen) versus strain at different strain-rates in SHPB tests. It can be seen that the maximum relative radial velocity between the specimen and the pressure bars varies in the range of 0.62 to 12 m/s for a common SHPB test when measured strain is less than 3.5%.
, at the edge of specimen) versus strain at different strain-rates in SHPB tests. It can be seen that the maximum relative radial velocity between the specimen and the pressure bars varies in the range of 0.62 to 12 m/s for a common SHPB test when measured strain is less than 3.5%.
In this velocity range, the so-called Stribeck curve is suitable to describe the variation of the friction coefficient with the relative velocity [35]. The friction coefficient has its maximum value at 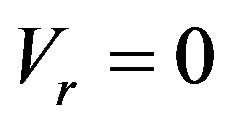 (i.e. the static friction coefficient,
(i.e. the static friction coefficient,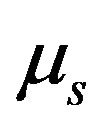 ) and then decreases considerably to its minimum value with the increase of the relative velocity in a small range and followed by a slow increase with the relative velocity. However, details of the relationship between the kinetic friction coefficient and the relative velocity depend upon the degree of surface roughness
) and then decreases considerably to its minimum value with the increase of the relative velocity in a small range and followed by a slow increase with the relative velocity. However, details of the relationship between the kinetic friction coefficient and the relative velocity depend upon the degree of surface roughness
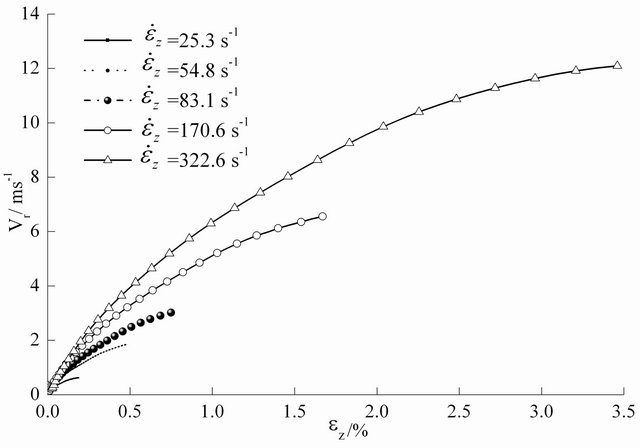
Figure 3. Variation of  with engineering axial strain
with engineering axial strain  with different values which are attained under various strain-rates in an SHPB test on mortar specimens.
with different values which are attained under various strain-rates in an SHPB test on mortar specimens.
and lubrication. For example, as the longitudinal pressure is applied, the lubricant will be pressurized, which could squeeze the lubricant out from the interface and/or increase the pore pressure of a thin layer lubricant fluid on the specimen. Such effects could influence the local stress state, and therefore, affect the SHPB measurements. The effects of the hydrodynamics of lubricants in SHPB tests were partly addressed in [36-39], which, however, demand further investigations.
In the 1960’s, the American Society for Lubrication Engineers (ASLE) listed more than 200 types of friction tests and equipment in use [40], and the list has since grown. However, within the test configurations described by Benzing [40], the relative velocity can only vary from 2.5 mm/s to 2.54 m/s depending on the apparatus [34]. SHPB techniques were also used to test the friction in high velocity (e.g. [32,41-46]). However, it is difficult to get a single friction-velocity equation over a wide range of relative velocities. Friction measurements under changed relative velocities will be conducted in order to relate the kinetic friction coefficient to the relative velocities for different engineering materials. The experiments here were designed to find the dependence of the kinetic friction coefficient on the relative velocity. Meng [34] used a simple apparatus which consists of a slip-way, a specimen and some measuring devices, as shown in Figure 4, for the measurement of the kinetic friction coefficient at a velocity of several meters per second. A highly sensitive capacitive accelerometer on a ceramic base with built-in electronics was used in the test, which can measure acceleration down to 0 Hz. The contact surface was lubricated by Shell Helix Super oil to simulate a similar situation in an SHPB test. The specimen slips from the top of the slip-way. Using the data of the acceleration history,  , the kinetic friction coefficient,
, the kinetic friction coefficient, 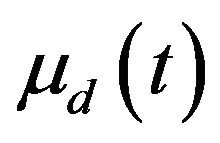 , between the specimen and the stain-less steel slip-way and the corresponding
, between the specimen and the stain-less steel slip-way and the corresponding 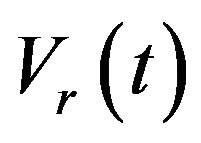 history can be obtained using the following formula [34],
history can be obtained using the following formula [34],
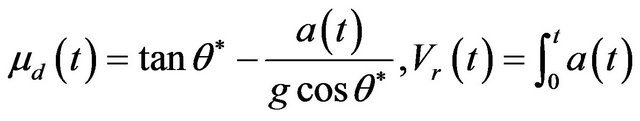 (3)
(3)
where  is the slope angle of the slip-way, and
is the slope angle of the slip-way, and 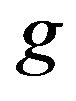 is the acceleration of gravity.
is the acceleration of gravity.
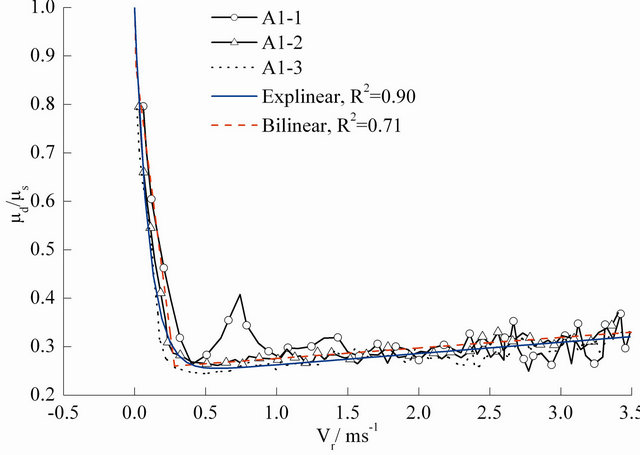
A series of tests were performed based on the equipment shown in Figure 4 to construct the kinetic friction model for engineering materials in common SHPB tests, and the results are shown in Figure 5, where the vertical coordinate is the ratio of the kinetic friction coefficient  to the static friction coefficient
to the static friction coefficient ,
,  , and the horizontal coordinate is
, and the horizontal coordinate is . In a practical numerical analysis, it is necessary to propose a simplified friction model to describe experimental results. Comparing with the Stribeck curve [34], it is reasonable to use an exponential-linear function to fit the testing results, i.e.
. In a practical numerical analysis, it is necessary to propose a simplified friction model to describe experimental results. Comparing with the Stribeck curve [34], it is reasonable to use an exponential-linear function to fit the testing results, i.e.
 (4)
(4)
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 4. Test apparatus: (a) Slip-way (side view); (b) Specimen; (c) Measuring devices; (d) Photo of the test apparatus [40].
(a) 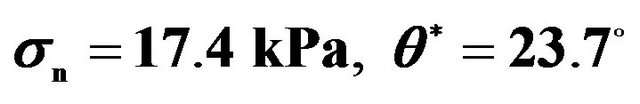

(b) 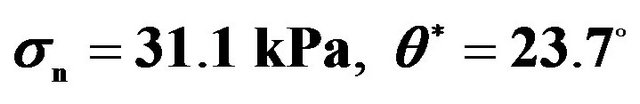

(c) 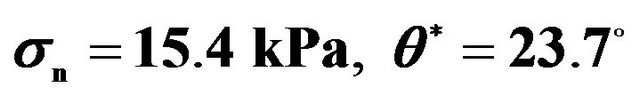

(d) 
(e) 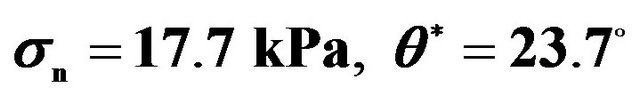
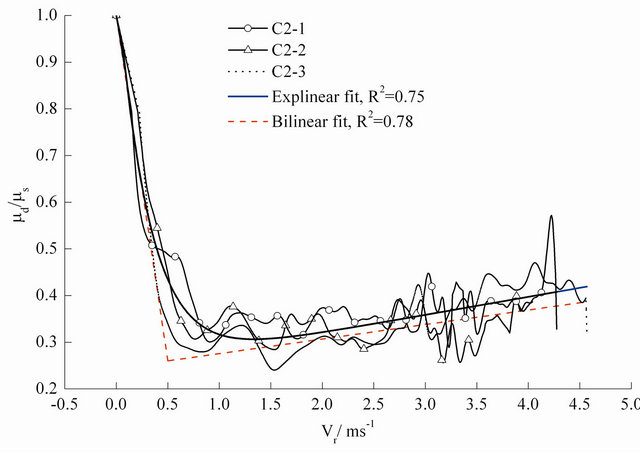
(f) 

(g) 

(h) 
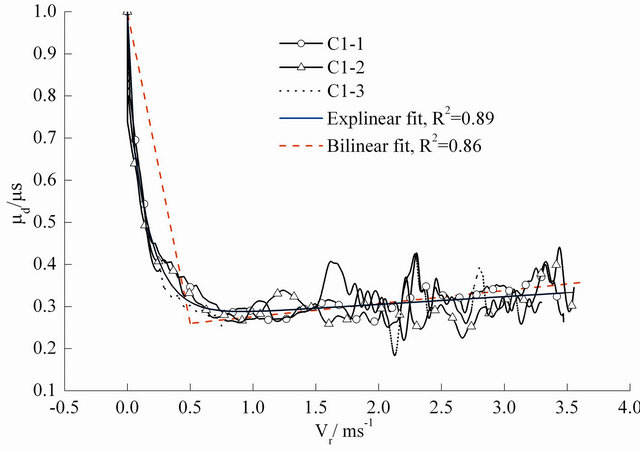
Figure 5. Variations of  with
with  based on repeat tests for (a) and (b) aluminum-alloy specimens (i.e. A1-# and A2-# where #Î1, 2, 3), for (c) and (d) polycarbonate (PC) specimens (i.e. P1-# and P2-# where #Î1, 2, 3), for (e) and (f) concrete specimens (i.e. C1-# and C2-# where #Î1, 2, 3), and for (g) and (h) mortar specimens (i.e. M1-# and M2-# where #Î1, 2, 3), under different normal stresses and slope angles, and fitted curves of these variations.
based on repeat tests for (a) and (b) aluminum-alloy specimens (i.e. A1-# and A2-# where #Î1, 2, 3), for (c) and (d) polycarbonate (PC) specimens (i.e. P1-# and P2-# where #Î1, 2, 3), for (e) and (f) concrete specimens (i.e. C1-# and C2-# where #Î1, 2, 3), and for (g) and (h) mortar specimens (i.e. M1-# and M2-# where #Î1, 2, 3), under different normal stresses and slope angles, and fitted curves of these variations.
in which 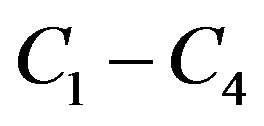 are constants obtained from the test results between
are constants obtained from the test results between  and
and , as shown in Table 1, and
, as shown in Table 1, and  when
when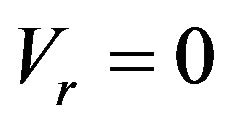 .
.
The coefficient of determination (Adj. R-Square, R2) between the experimental data and fitted curves obtained from Origin 8.0 is also shown in Figure 5. It is observed
Table 1. Constants in Equation (4).
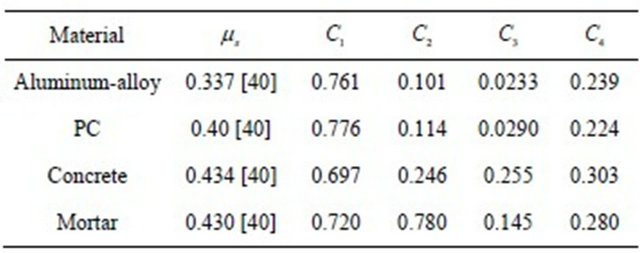
that under the same slope angle, the value of R2 will be reduced with the increase of normal pressure; while under the nearly same normal pressure, the value of R2 will also be reduced with increasing the slope angle. The exponential-linear function is better than the bilinear function used in Ref. [34] to fit the kinetic friction coefficient, as the former can be easily input into numerical simulations. The maximum relative velocity in the present tests (up to 4.6 m/s) covers the relative velocity range in typical SHPB tests of engineering materials studied in this paper because Equation (2) is based on the incompressibility of the specimen and the neglect of Poisson’s effect in the pressure bar material. When the elastic deformation of an SHPB specimen and the lateral movement of the pressure bars are considered, the relative velocity between the specimen faces and the pressure bars is smaller than that estimated by Equation (2).
3. Discussion
To study the friction effect on the SHPB results using the constant friction model and the proposed kinetic friction model, taking mortar as an example, four cases were simulated with different values of 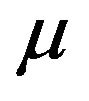 based on the constitutive equation and numerical SHPB model of mortar as described in Ref. [18], i.e. 1)
based on the constitutive equation and numerical SHPB model of mortar as described in Ref. [18], i.e. 1) , which corresponds to the frictionless case; 2)
, which corresponds to the frictionless case; 2)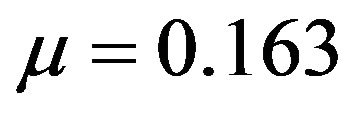 , corresponding to
, corresponding to , which is the minimum value of Equation (4) for mortar; 3)
, which is the minimum value of Equation (4) for mortar; 3)  where
where  is given by Equation (4), which is implemented into ABAQUS using a user subroutine VFRIC; 4)
is given by Equation (4), which is implemented into ABAQUS using a user subroutine VFRIC; 4) 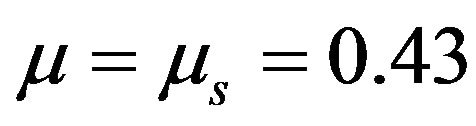 for mortar, which is the static friction coefficient. The simulation results under the strain-rate of 170 s−1 corresponding to the peak strength of mortar specimens with the ratio of length to diameter
for mortar, which is the static friction coefficient. The simulation results under the strain-rate of 170 s−1 corresponding to the peak strength of mortar specimens with the ratio of length to diameter 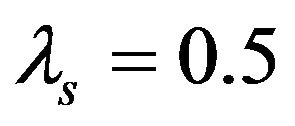 and
and , are shown in Figure 6. It is observed that the maximum difference among cases 1-3 is about 15%. However, a large difference between case 4 and three other cases is observed. A constant friction coefficient of zero and the kinetic friction model are applied in the finite element analysis of SHPB tests for mortar specimens of
, are shown in Figure 6. It is observed that the maximum difference among cases 1-3 is about 15%. However, a large difference between case 4 and three other cases is observed. A constant friction coefficient of zero and the kinetic friction model are applied in the finite element analysis of SHPB tests for mortar specimens of  mm and
mm and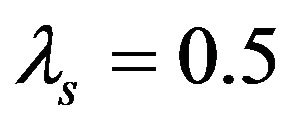 . Comparison results of friction contribution to the dynamic compressive strength enhancement are shown in Figure 7. In Figure 7, the vertical coordinate is the dynamic increase factor (DIF), defined as the ratio of dynamic compressive strength under the
. Comparison results of friction contribution to the dynamic compressive strength enhancement are shown in Figure 7. In Figure 7, the vertical coordinate is the dynamic increase factor (DIF), defined as the ratio of dynamic compressive strength under the

Figure 6. Comparison of calculated results for different friction models at the strain-rate of 170 s−1 corresponding to the peak strength of mortar specimens with 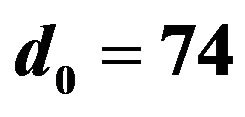 mm and
mm and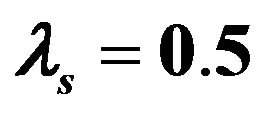 .
.

Figure 7. Contribution of friction to the dependence of the dynamic increase factor (DIF) on strain-rate in the numeric SHPB tests when using different friction models for mortar specimens with mm and
mm and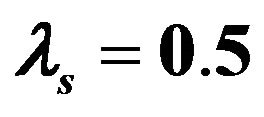 .
.
testing strain-rate to quasi-static compressive strength, which represents the dynamic compressive strength enhancement of mortar specimens testing on SHPB set-up. It is observed from Figure 7 that DIFs obtained from numerical SHPB simulations when using the kinetic friction model are greater than those predicted based on the frictionless assumption in the strain-rate range of 101 - 103 s−1, especially when the strain-rate is greater than the transition strain-rate (the critical strain-rate where strainrate dependence of DIF starts to increase apparently). There seems to be no remarkable difference in the transition strain-rate between the frictionless model and kinetic model. The end friction effect described by the kinetic friction model induces higher hydrostatic pressure on the mortar specimens comparing with not considering the end friction effect (frictionless), and higher dynamic compressive strength of mortar specimens will be obtained from numerical SHPB simulations as the mechanical behavior of mortar is hydrostatic-pressure-dependent.
Therefore, the DIF predicted from the kinetic friction model is higher than that from the frictionless model at the same strain-rate. Thus, a more reliable assessment and correction procedure for SHPB tests should be based on the kinetic friction model whenever the results of kinetic friction coefficient versus the relative velocity are available.
4. Conclusion
Friction on the bar/specimen interfaces is one of the possible error sources of the SHPB tests and should be examined in the assessment and correction procedure for SHPB results through numerical analyses. The simple device is capable of providing the kinetic interface friction test results for common SHPB tests. Based on the numerical analyses which implement the proposed kinetic interface friction model, it is found that the difference between the constant friction model and kinetic interface friction model may cause different results. Thus, whenever it is possible, a more reliable assessment and correction procedure for the SHPB test should be based on a kinetic friction model.
5. Acknowledgements
We acknowledge the support by Scientific Research Fund of Sichuan Provincial Education Department (10zd1012), and the Doctorate Foundation of Southwest University of Science and Technology (10zx7141).
REFERENCES
- ASME, “#242 Split-Hopkinson Pressure Bar Apparatus,” 2010. http://www.asme.org/Communities/History/Landmarks/241_SwRI_SplitHopkinson.cfm
- P. Hartley, C. E. N. Sturgess and G. W. Rowe, “Influence of Friction on the Prediction of Forces, Pressure Distributions and Properties in Upset Forging,” International Journal of Mechanical Sciences, Vol. 22, No. 12, 1980, pp. 743-753. doi:10.1016/0020-7403(80)90059-4
- J. R. Klepaczko and Z. Malinowski, “Dynamic Frictional Effects as Measured from the Split Hopkinson Pressure Bar,” In: K. Kawata and J. Shioiri, Eds., High Velocity Deformation of Solids, Springer-Verlag, Berlin, 1978, pp. 403-416.
- D. A. Gorham, P. H. Pope and O. Cox, “Sources of Error in Very High Strain Rate Compression Tests,” In: J. Harding, Ed., Mechanical Properties at High Rates of Strain, Institution of Physics Conference Series, Oxford, 1984, No. 70, pp. 151-158.
- J. Mescall, R. Papirno and J. Mclaughlin, “Stress and Deformation States Associated with Upset Tests in Metals,” In: R. Chait and R. Papirno, Eds., Compression Testing of Homogeneous Materials and Composite, American Society for Testing and Materials, Philadelphia, 1983, pp. 7- 23. doi:10.1520/STP36193S
- J. A. Schey, T. R. Venner and S. L. Takomana, “The Effect of Friction on Pressure in Upsetting at Low Diameter-to-Height Ratios,” Journal of Mechanical Working Technology, Vol. 6, No. 1, 1982, pp. 23-33. doi:10.1016/0378-3804(82)90017-1
- J. K. Bannerjee, “Barreling of Solid Cylinders under Axial Compression,” Journal of Engineering Materials and Technology, Vol. 107, No. 2, 1985, pp. 138-144. doi:10.1115/1.3225789
- J. K. Bannerjee and G. Cárdenas, “Numerical Analysis on the Barreling of Solid Cylinders under Axisymmetric Compression,” Journal of Engineering Materials and Technology, Vol. 107, No. 2, 1985, pp. 145-147. doi:10.1115/1.3225790
- R. Narayanasamy and K. S. Pandey, “Phenomenon of Barrelling in Aluminium Solid Cylinders during Cold Upset-Forming,” Journal of Materials Processing Technology, Vol. 70, No. 1-3, 1997, pp. 17-21. doi:10.1016/S0924-0136(97)00035-6
- E. Parteder and R. Bünten, “Determination of Flow Curves by Means of a Compression Test under Sticking Friction Conditions Using an Iterative Finite Element Procedure,” Journal of Materials Processing Technology, Vol. 74, No. 1-3, 1998, pp. 227-233. doi:10.1016/S0924-0136(97)00275-6
- W. Ohnson, G. L. Baraya and R. A. C. Slater, “On Heat Lines or Lines of Thermal Discontinuity,” International Journal of Mechanical Sciences, Vol. 6, No. 6, 1964, pp. 409-414. doi:10.1016/S0020-7403(64)80001-1
- Y. L. Bai and B. Dodd, “Adiabatic Shear Localization: Occurrence, Theories and Applications,” 1st Edition, Pergamon, Oxford, 1992.
- A. Jenner, Y. L. Bai and B. Dodd, “A Thermo-Plastic Shear Instability Criterion Applied to Surface Cracking in Upsetting and Related Processes,” The Journal of Strain Analysis for Engineering Design, Vol. 16, No. 3, 1981, pp. 159-164. doi:10.1243/03093247V163159
- L. D. Bertholf and C. H. Karnes, “Two Dimensional Analysis of the Split Hopkinson Pressure Bar System,” Journal of the Mechanics and Physics of Solids, Vol. 23, No. 1, 1975, pp. 1-19. doi:10.1016/0022-5096(75)90008-3
- J. Z. Malinowski and J. R. Klepaczko, “A Unified Analytic and Numerical Approach to Specimen Behaviour in the Split-Hopkinson Pressure Bar,” International Journal of Mechanical Sciences, Vol. 28, No. 6, 1986, pp. 381- 391. doi:10.1016/0020-7403(86)90057-3
- D. A. Gorham, “The Effect of Specimen Dimensions on High Strain Rate Compression Measurements of Copper,” Journal of Physics D: Applied Physics, Vol. 24, No. 8, 1991, pp. 1489-1492. doi:10.1088/0022-3727/24/8/041
- Q. M. Li and H. Meng, “About the Dynamic Strength Enhancement of Concrete-Like Materials in a Split Hopkinson Pressure Bar Test,” International Journal of Solids and Structures, Vol. 40, No. 2, 2003, pp. 343-360. doi:10.1016/S0020-7683(02)00526-7
- Q. M. Li, Y. B. Lu and H. Meng, “Further Investigation on the Dynamic Compressive Strength Enhancement of Concrete-Like Materials Based on Split Hopkinson Pressure Bar Tests, Part II: Numerical Simulations,” International Journal of Impact Engineering, Vol. 36, No. 12, 2009, pp. 1335-1345. doi:10.1016/j.ijimpeng.2009.04.010
- H. Meng and Q. M. Li, “Correction between the Accuracy of a SHPB Test and the Stress Uniformity Based on Numerical Experiments,” International Journal of Impact Engineering, Vol. 28, No. 5, 2003, pp. 537-555. doi:10.1016/S0734-743X(02)00073-8
- B. Avitzur, “Forging of Hollow Discs,” Israel Journal of Technology, Vol. 2, No. 3, 1964, pp. 295-304.
- B. Avitzur, “Metal Forming: Processes and Analysis,” McGraw-Hill, New York, 1968.
- B. Avitzur and F. Sauerwine, “Limit Analysis of Hollow Disk Forging. Part 1: Upper Bound,” Journal of Engineering for Industry, Vol. 100, No. 3, 1978, pp. 340-344. doi:10.1115/1.3439437
- B. Avitzur and C. J. Van Tyne, “Ring Forming: An Upper Bound Approach. Part 2: Process Analysis and Characteristics,” Journal of Engineering for Industry, Vol. 104, No. 3, 1982, pp. 238-247. doi:10.1115/1.3185825
- B. Avitzur and C. J. Van Tyne, “Ring Forming: An Upper Bound Approach. Part 3: Constrained Forging and Deep Drawing Applications,” Journal of Engineering for Industry, Vol. 104, No. 3, 1982, pp. 248-252. doi:10.1115/1.3185826
- B. Avitzur and R. A. Kohser, “Disk and Strip Forging for the Determination of Friction and Flow Strength Values,” Tribology Transactions, Vol. 21, No. 2, 1978, pp. 143- 151. doi:10.1080/05698197808982870
- B. Avitzur and C. J. Van Tyne, “Ring Forming: An Upper Bound Approach. Part 1: Flow Pattern and Calculation of Power,” Journal of Engineering for Industry, Vol. 104, No. 3, 1982, pp. 231-237. doi:10.1115/1.3185824
- S. M. Walley, J. E. Field, P. H. Pope and N. A. Safford, “A Study of the Rapid Deformation Behaviour of a Range of Polymers,” Philosophical Transactions of Royal Society A, Vol. 328, No. 1597, 1989, pp. 1-33. doi:10.1098/rsta.1989.0020
- S. M. Walley, J. E. Field, P. H. Pope and N. A. Safford, “The Rapid Deformation Behaviour of Various Polymers,” Journal de Physique III France, Vol. 1, No. 12, 1991, pp. 1889-1925. doi:10.1051/jp3:1991240
- S. M. Walley, P. D. Church, M. Furth and J. E. Field, “A High-Speed Photographic Study of the Rapid Deformation of Metal Annuli: A Comparison of Theory with Experiment,” Journal de Physique IV France, Vol. 7, No. C3, 1997, pp. 317-322. doi:10.1051/jp4:1997356
- E. Siebel, “Fundamentals for the Calculation of Power and Working Requirements in Forging and Rolling-Mill Practice (Grundlagen zur Berechnung des Kraftund Arbeitsbedarf beim Schmieden und Walzen),” Stahl und Eisen, Vol. 43, 1923, pp. 1295-1298. (in German)
- B. J. Briscoe and R. W. Nosker, “The Influence of Interfacial Friction on the Deformation of High Density Polyethylene in a Split Hopkinson Pressure Bar,” Wear, Vol. 95, No. 3, 1984, pp. 241-262. doi:10.1016/0043-1648(84)90140-6
- X. Y. Wang, F. Y. Lu and Y. L. Lin, “Study on Interfacial Friction Effect in the SHPB Tests,” Explosion and Shock Waves, Vol. 26, No. 2, 2006, pp. 134-139. (in Chinese)
- F. Y. Lin, D. S. Zhang and X. D. Ma, “Study on the Friction Characteristics of Polyurethane for the Friction Linear of Hoisting,” Lubrication Engineering, Vol. 2, No. 33-34, 2000, p. 60. (in Chinese)
- H. Meng, “Numerical Split Hopkinson Pressure Bar (NSHPB) Test and Its Applications in the Assessment and Improvement of SHPB Test Results,” Ph.D. Thesis, Nanyang Technological University, Singapore, 2002.
- D. Pavelescu and A. Tudor, “The Sliding Friction Coefficient—Its Evolution and Usefulness,” Wear, Vol. 120, No. 3, 1987, pp. 321-336. doi:10.1016/0043-1648(87)90025-1
- G. I. Taylor, “Plastic Strain in Metals,” Journal of the Institute of Metals, Vol. 62, 1938, pp. 307-324.
- J. A. C. Martins, J. T. Oden and F. M. F. Simoes, “A Study of Static and Kinetic Friction,” International Journal of Engineering Sciences, Vol. 28, No. 1, 1990, pp. 29- 92. doi:10.1016/0020-7225(90)90014-A
- B. A. Hélouvry, P. Dupont and C. C. D. Wit, “A Survey of Models, Analysis Tools and Compensation Methods for the Control of Machines with Friction,” Automatica, Vol. 30, No. 7, 1994, pp. 1083-1138. doi:10.1016/0005-1098(94)90209-7
- D. P. Hess and A. Soom, “Friction at a Lubricated Line Contact Operating at Oscillating Sliding Velocities,” Journal of Tribology, Vol. 112, No. 1, 1990, pp. 147-152. doi:10.1115/1.2920220
- R. Benzing, I. Goldblatt and V. Hopkins, et al., “Friction and Wear Devices,” 2nd Edition, ASLE, IL Park Ridge, 1976.
- K. Ogawa, “Impact Friction Test Method by Applying Stress Wave,” Experimental Mechanics, Vol. 37, No. 4, 1997, pp. 398-402. doi:10.1007/BF02317304
- V. Prakash, “Time Resolved Friction with Applications to High Speed Machining,” Tribology Transactions, Vol. 41, No. 2, 1998, pp. 189-198. doi:10.1080/10402009808983738
- S. Rajagopalan and V. Prakash, “A Modified Torsional Kolsky Bar for Investigating Dynamic Friction,” Experimental Mechanics, Vol. 39, No. 4, 1999, pp. 295-303. doi:10.1007/BF02329808
- H. Zhang, A. Patanella and H. D. Espinosa, et al., “Dynamic Friction of Nano-Materials,” AIP Conference Proceedings, Vol. 505, No. 1, 2000, pp. 1225-1228. doi:10.1063/1.1303682
- H. D. Espinosa, A. Patanella and M. Fischer, “A Novel Dynamic Friction Experiment Using a Modified Kolsky Bar Apparatus,” Experimental Mechanics, Vol. 40, No. 2, 2000, pp. 138-153. doi:10.1007/BF02325039
- Y. L. Lin, F. Y. Lu and Y. X. Cui, “Testing of Friction Coefficients of Material Loaded by Shock Wave,” Tribology, Vol. 27, No. 1, 2007, pp. 64-67. (in Chinese)
NOTES
*Corresponding author.

