Modern Mechanical Engineering
Vol.2 No.4(2012), Article ID:24895,7 pages DOI:10.4236/mme.2012.24017
Numerical Study on Application of CuO-Water Nanofluid in Automotive Diesel Engine Radiator
1Department of Mechanical Engineering, Abadan Branch, Islamic Azad University, Abadan, Iran
2Department of Mechanical Engineering, College of Engineering, Trivandrum, India
Email: *N.Bozorgan@gmail.com
Received August 15, 2012; revised September 17, 2012; accepted September 29, 2012
Keywords: Automotive Diesel Engine Radiator; CuO-Water Nanofluid; Turbulent Flow; Heat Transfer; Pumping Power
ABSTRACT
Application of CuO-water nanofluid with size of the nanoparticles of 20 nm and volume concentrations up 2% is numerically investigated in a radiator of Chevrolet Suburban diesel engine under turbulent flow conditions. The heat transfer relations between airflow and nanofluid coolant have been obtained to evaluate local convective and overall heat transfer coefficients and also pumping power for nanofluid flowing in the radiator with a given heat exchange capacity. In the present study, the effects of the automotive speed and Reynolds number of the nanofluid in the different volume concentrations on the radiator performance are also investigated. The results show that for CuO-water nanofluid at 2% volume concentration circulating through the flat tubes with Renf = 6000 while the automotive speed is 70 km/hr, the overall heat transfer coefficient and pumping power are approximately 10% and 23.8% more than that of base fluid for given conditions, respectively.
1. Introduction
Cooling is one of the top technical challenges to obtain the best automotive design in multiple aspects (performance, fuel consumption, aesthetics, safety, etc.). Automotive radiator is an important part of the engine cooling system. Due to limited space at the front of the engine, the size of the radiator is restricted and cannot be essentially increased. Therefore, it is necessary to increase the heat transfer capabilities of working fluids such as water and ethylene glycol in radiators because of their low thermal conductivity. A recent advancement in nanotechnology has been the introduction of nanofluids, i.e. colloidal suspensions of nanometer-sized solid particles instead of common working fluids. Nanofluids were first innovated by Choi [1] in 1995 at the Argonne National Laboratory, USA. Compared with traditional solid-liquid suspensions containing millimeter or micrometer sized particles, nanofluids as coolants in the heat exchangers have shown better heat transfer performance because of small size of suspend solid particles. It causes that nanofluids have a behavior similar to base liquid molecules. Because of their excellent thermal performance, nanofluids have attracted attention as a new generation of heat transfer fluids in building heating, in heat exchangers, in chemical plants and in automotive cooling applications. Recently there have been considerable research findings highlighting superior heat transfer performances of nanofluids. Peyghambarzadeh et al. [2] investigated experimentally the convective heat transfer enhancement of water and EG based nanofluids consisting of Al2O3 nanoparticles up 1% volume concentration as the coolants inside flat aluminum tubes of the car radiator under laminar and turbulent flows. The results show that the heat transfer enhances about 40% compared with the base fluids in the best conditions. Ollivier et al. [3] investigated the use of nanofluids as a jacket water coolant in a gas spark ignition engine. They numerically simulated the unsteady heat transfer through the cylinder and inside the coolant flow and reported that because of higher thermal diffusivity of nanofluids, the thermal signal variations for knock detection increased by 15% over the predicted using pure water. Vajjha et al. [4] numerically investigated the heat transfer augmentation by application of two different nanofluids consisting of Al2O3 and CuO nanoparticles in an ethylene glycol and water mixture circulating through the flat tubes of an automobile radiator. The numerical results showed that at a Reynolds number of 2000, the percentage increase in the average heat transfer coefficient over the base fluid for a 10% Al2O3 nanofluid was 94% and that for a 6% CuO nanofluid was 89%. Also the average heat transfer coefficient increases with the Reynolds number and also with the particle volumetric concentration. Leong et al. [5] have studied the application of nanofluids as working fluids in shell and tube heat recovery exchangers in a biomass heating plant and showed that about 7.8% of the heat transfer enhancement could be achieved with the addition of 1% copper nanoparticles in ethylene glycol based fluid at 26.3 kg/s and 111.6 kg/s mass flow rate for flue gas and coolant, respectively. Ijam et al. [6] theoretically analyzed a minichannel heat sink with a 20 × 20 cm bottom for SiC-water and TiO2-water nanofluids as the coolants through hydraulic diameters under turbulent flow. Their results showed a maximum enhancement of 12.44% in thermal conductivity for SiC-water and 9.99% for TiO2-water at 4% of volume fraction. Also the maximum improvement in heat flux by using SiC-water and TiO2-water nanofluids at 4% of volume fraction for inlet velocities of 2 and 6 m/s is calculated by ~7.63%, 12.43% and 7.25%, 12.43%, respectively. In 2012 Saeedinia et al. [7] applied CuO-base oil particles varying in the range of 0.2% - 2% inside a circular tube and showed that the CuO nanoparticles suspended in base-oil increases the heat transfer coefficient even for a very low particle concentration of 0.2% volume concentration. They found a maximum heat transfer coefficient enhancement of 12.7% for 2% CuO nanofluid. Shafahi et al. [8] used a two-dimensional analysis to study the thermal performance of a cylindrical heat pipe utilizing Al2O3, CuO and TiO2 nanofluids. Their results confirmed that the thermal performance of a heat pipe is improved and temperature gradient along the heat pipe and thermal resistance across the heat pipe are reduced and maximum capillary heat transfer of the heat pipe is observed when nanofluids are utilized as the working fluid.
In the present paper, 20 nm-CuO/water nanofluid with concentration up 2 vol% has been numerically studied as a coolant in a radiator of Chevrolet Suburban diesel engine with a given heat exchange capacity. It shall be noted that metal oxides such as CuO nanoparticles are chemically more stable than their metallic counterparts.
2. Analysis
In order to investigate the heat transfer performance of nanofluids and use them in practical applications, it is necessary first to study their thermophysical properties such as density, specific heat, viscosity and thermal conductivity. In this study, to validate the numerical results, the methodology employed to determine the efficiency of CuO-water nanofluid as coolant in a radiator of Chevrolet Suburban diesel engine with a given heat exchange capacity is based on new rheological and thermophysical properties correlations developed from experiments.
2.1. Prediction of Thermophysical Properties
At the first step, the heat characteristics of the nanofluid have been evaluated and at the next step the application of nanofluid coolant has been investigated to improve the heat transfer performance of the radiator. This radiator consists of 644 brass flat tubes and 346 continuous copper fins [9,10]. The main characteristics of radiator are listed in Table 1 that useful for assessing the radiator performance in this work. However, following assumptions are made:
• The flow is an incompressible, steady state and turbulent.
• The effect of body force is neglected.
• The thermophysical properties of nanofluids are constant.
The characteristics of nanoparticles and base fluid used in this study are summarized in Table 2. The necessary thermophysical properties in this paper are density, viscosity, specific heat and thermal conductivity.
In this paper, density (ρnf) and special heat capacity (cp,nf) of CuO/water nanofluid have been calculated based on empirical correlations proposed by Pak [11] and Xuan [12] as follows:
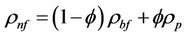 (1)
(1)
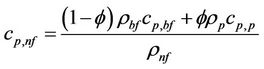 (2)
(2)
where 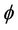 is nanoparticle volume concentration and ρp, ρbf and cp,p, cp,bf are the densities and the specific heats of
is nanoparticle volume concentration and ρp, ρbf and cp,p, cp,bf are the densities and the specific heats of
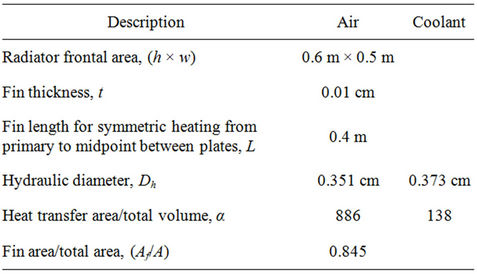
Table 1. Radiator specifications.

Table 2. Thermophysical properties of base fluid and nanoparticles.
the nanoparticles and base fluid, respectively.
Also, thermal conductivity (knf) and viscosity (μnf) for nanofluid have been estimated based on two semi-empirical equations presented by Corcione [13] in 2011 on the basis of a wide variety of experimental data available in the literature as following equations:
 (3)
(3)
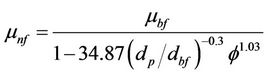 (4)
(4)
where kbf is the thermal conductivity of the base fluid, Re is the nanoparticle Reynolds number, Prbf is the Prandtl number of the base fluid, T is the nanofluid temperature, Tfr is the freezing point of the base fluid, kp is the thermal conductivity of the nanoparticles, μbf is the dynamic viscosity of the base fluid, dp is the diameter of the nanoparticles and dbf is the equivalent diameter of a base fluid molecule. The standard deviations of error of Equations (3) and (4) are 1.86% and 1.84%, respectively.
In more detail, the Reynolds number of the suspended nanoparticles can be calculated as follows [13]:
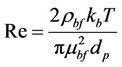 (5)
(5)
where in kb = 1.38066 × 10−23 J/K is the Boltzmann constant.
2.2. Heat Transfer and Pressure Drop Modeling
2.2.1. Heat Transfer Modeling
The rate of heat transferred between nanofluid coolant and airflow in the radiator can be written as follows:
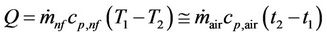 (6)
(6)
where nf and air denote the relevant parameters of nanofluid coolant and airflow. Here, T1 = 110˚C and T2 = 49˚C are the inlet and outlet temperatures of nanofluid coolant, t1 = 32˚C is the inlet air temperature and outlet air temperature (t2) can be calculated as:
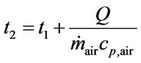 (7)
(7)
The mass flowrates are calculated based on the pump flowrate for water and the speed and frontal area for the air as follows:
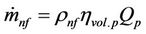 (8)
(8)
 (9)
(9)
Here, the Bosch Cobra pump is used with flowrate of Qp = 317 gallons/hour and volumetric efficiency (hvol.p) by 80%. In Equation (9), VAutomotive is the automotive speed.
The total heat transfer area of the radiator, A, is computed from the following equation:
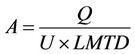 (10)
(10)
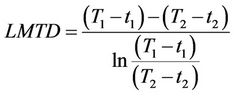 (11)
(11)
In Equation (10), U is the overall heat transfer coefficient which is expressed in the following form [9]:
 (12)
(12)
where hair is the heat transfer coefficient of air, ho is the total surface temperature effectiveness, hnf is the heat transfer coefficient of nanofluid coolant and Rf is the fouling resistance that is assumed to be 5 × 10−4 m2·KW−1. In the present study, the heat transfer coefficient of air is calculated as:
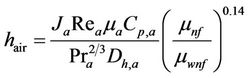 (13)
(13)
In the above equation,  is the viscosity correction factor that is defined as the ratio of viscosity of the nanofluid at the mean temperature of inlet and outlet conditions to that one at the mean temperature of wall tube and also cp,air = 1007 J·kg−1·K−1, Pra = 0.7057, μa = 0.00001889 (Nsm−2)
is the viscosity correction factor that is defined as the ratio of viscosity of the nanofluid at the mean temperature of inlet and outlet conditions to that one at the mean temperature of wall tube and also cp,air = 1007 J·kg−1·K−1, Pra = 0.7057, μa = 0.00001889 (Nsm−2)
In Equation (13), Reynolds number and Colburn factor for the air are calculated with considering the air properties as follows:
 (14)
(14)
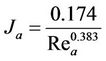 (15)
(15)
where Ga is the mass flow rate of air. In Equation (12), the total surface temperature effectiveness is expressed as:
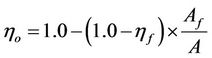 (16)
(16)
where hf is the fin efficiency of plate fin which is defined as follows:
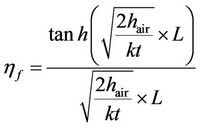 (17)
(17)
Here, k = 377 Wm−1·K−1 is thermal conductivity of copper fin.
The heat transfer coefficient of the nanofluid coolant (hnf) flowing in the flat tubes can be calculated with considering the turbulent Nusselt number presented by Li and Xuan [14] as follows:
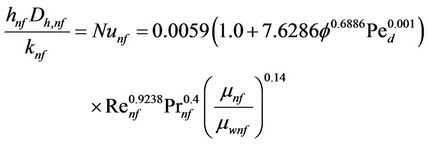 (18)
(18)
where Ped is the nanofluid Peclet number and is defined in the following form:
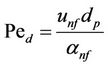 (19)
(19)
where αnf is the nanofluid thermal diffusivity which is defined as follows:
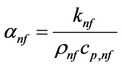 (20)
(20)
The Reynolds and Prandtl numbers in Equation (18) are calculated with considering the nanofluid properties as follows:
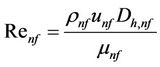 (21)
(21)
 (22)
(22)
2.2.2. Pressure Drop Modeling
In the present paper, the fanning friction factor (fn), the pressure drop (Δpnf) and pumping power (PP) for CuO- water nanofluid coolant flowing in the flat tubes are calculated as follows [10]:
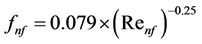 (23)
(23)
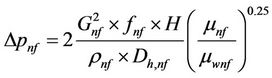 (24)
(24)
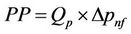 (25)
(25)
In Equation (24), H is the total nanofluid flow length which is obtained as:
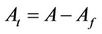 (26)
(26)
 (27)
(27)
where At is the total heat transfer area of flat tubes.
3. Simulation Results and Discussion
3.1. Local Heat Transfer
In Figure 1 the ratio of thermal conductivity and heat transfer coefficient of nanofluid in comparison with the base fluid (kr and hr) emphasize the local heat transfer augmentation. This analysis is carried out at Renf = 6000. This figure reveals that as the concentration increases, the effect of increasing nanoparticles concentration on changing the thermal conductivity is lower than changing the heat transfer coefficient. As an example, for a volume concentration of 2 vol%, the local heat transfer coefficient ratio is about hr = 2.05 while the thermal conductivity ratio is kr = 1.55. Figure 2 shows the effect of nanoparticles concentration on the heat transfer coefficient and Nusselt number. Results show that the heat transfer coefficient and Nusselt number can be enhanced by adding nanoparticles to the base fluid. Enhancement of heat transfer by the nanofluid may be resulted from the following two aspects: first the incremented particles which increase the thermal conductivity of the mixture; second, chaotic movement of ultrafine particles accelerates the energy exchange between the fluid and the wall of the heat exchanger. However, it should be noted that increasing the particles concentration raises the fluid viscosity and decreases the Reynolds number and consequently decreases the local heat transfer behavior. But the results shown in Figures 1 and 2 indicate that increasing in particles concentration raises the heat transfer coefficient. This is due to the fact that the change in the thermal conductivity is more effective than the change in

Figure 1. Comparison between kr and hr for CuO-water nanofluid coolant in the radiator at different volume fractions.
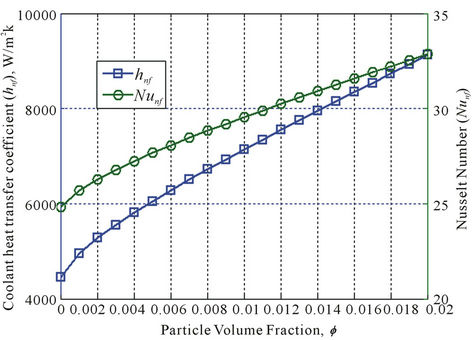
Figure 2. The Local heat transfer coefficient and Nusselt number for CuO-water nanofluid coolant at various concentrations.
the fluid viscosity on heat transfer enhancement of nanofluid at higher concentration.
3.2. Overall Heat Transfer
Figures 3-5 show the results of simulating the effects of using CuO-water nanofluid coolant with different volume fractions flowing in the flat tubes in the various ranges of the automotive speed and Reynolds number of the nanofluid on the overall heat transfer coefficient. The results of this study show that nanofluid enhances the overall heat transfer coefficient in the radiator and therefore the total heat transfer area of the radiator can be reduced.
Figure 3 shows the overall heat transfer coefficient for CuO-water nanofluid coolant in an automotive radiator that has been calculated by Equation (12). In this analysis, Reynolds number of the nanofluid is 6000 and the automotive speed is assumed to be 70 km/hr. As shown in this figure, the overall heat transfer coefficient is high when the probability of collision between nanoparticles and the wall of the flat tubes has increased under higher concentration conditions. It confirms that nanofluids have considerable potential to use in the automotive radiator. A further inspection of Figure 3 shows that the overall heat transfer coefficient of the CuO-water nanofluid for volume concentrations in the range of 0.1% to 2% is about 122 and 134.27 W/m2k, respectively.
The coolant Reynolds number has an important role in determining the radiator performance. The coolant Reynolds number must be properly controlled by thermostating pump because engine might be overcooled or overheated. Therefore, the effect of the coolant Reynolds number on the radiator performance at an automotive speed of 70 km/hr has been studied in this paper. According to Figure 4, the increase in the coolant Reynolds number increases the overall heat transfer coefficient that
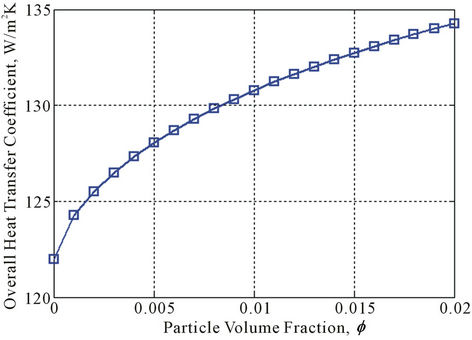
Figure 3. Variations of overall heat transfer coefficient for nanofluid at different volume fractions.

Figure 4. Effect of coolant Reynolds number on overall heat transfer coefficient in the radiator.
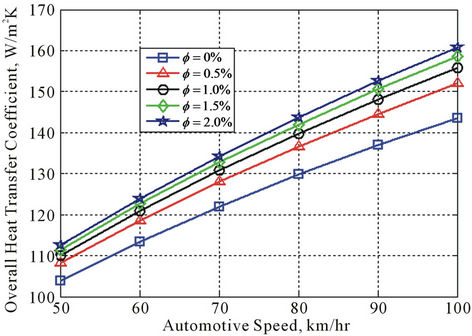
Figure 5. Effects of the automotive speed and CuO volume fraction on overall heat transfer coefficient in the radiator.
the magnitude of this property for CuO-water nanofluid at higher concentration is more than that of a base fluid. For instance, the results show that the increase in overall heat transfer coefficient for 2% CuO-water nanofluid at Renf = 8000 compared with Renf = 6000 is about 2.3%.
As well as, the automotive speed plays an important role in the radiator performance. As expected, the mass flowrate of the air increases with increasing the automotive speed and therefore Reynolds number and mass velocity for the air increase. Increasing the air Reynolds number raises the air mass velocity (refer to Equation (14)) and decreases the air Colburn factor (refer to Equation (15)). But the results shown in Figure 5 indicate that increasing in automotive speed and air Reynolds number raises the overall heat transfer coefficient because of the increase in air heat transfer coefficient. Therefore, it can be concluded that the change in the air mass velocity is more than the change in Colburn factor with increasing the air Reynolds number. In the analysis shown in Figure 5, the overall heat transfer coefficient of the radiator is calculated for the fixed coolant Reynolds number of 6000 at different volume fractions. For instance, the results show that the increase in overall heat transfer coefficient for 2% CuO-water nanofluid at automotive speed of 80 km/hr compared with 60 km/hr is about 16%.
3.3. Pumping Power
In order to apply the nanofluids for practical application, in addition to the heat transfer performance it is necessary to study their flow features. With increasing nanoparticles loading in the base fluid, viscosity and density of the nanofluids increase and therefore the friction factor and the pressure drop must be increased. Hence, nanofluids generally require the greater pumping power than their base fluid. In the present paper, the pumping power for CuO-water nanofluid coolant flowing in the flat tubes in the various ranges of the coolant Reynolds number (at VAutomotive = 70 km/hr) and the automotive speed (at Renf = 6000) are calculated and shown in Figures 6 and 7. For instance, Figure 6 shows that the increase in pumping power for 2% CuO-water nanofluid at Renf = 8000 compared with Renf = 6000 is about 61.75%. Also as an example, Figure 7 shows that the decrease in pumping power for 2% CuO-water nanofluid at the automotive speed of 80 km/hr compared with 60 km/hr is about 16.7%.
4. Conclusion
This paper presented a numerical investigation of the use of CuO-water nanofluid as a coolant in a radiator of Chevrolet Suburban diesel engine with a given heat exchange capacity. The local convective and overall heat transfer coefficients and pumping power for CuO-water nanofluid at different volume fractions (0.1% - 2%) was studied under turbulent flow conditions. Also, the effects of the coolant Reynolds number and the automotive speed on the radiator performance are considered in this
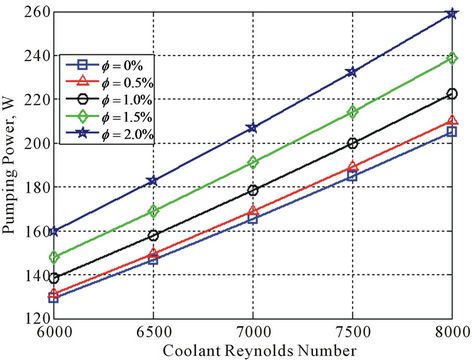
Figure 6. Effect of coolant Reynolds number on pumping power in the radiator.

Figure 7. Effect of the automotive speed on pumping power for nanofluid with different volume fractions in the radiator.
work. The simulation results indicate that the overall heat transfer coefficient of nanofluid is greater than that of water alone and therefore the total heat transfer area of the radiator can be reduced. However, the considerable increase in associated pumping power may impose some limitations on the efficient use of this type of nanofluid in automotive diesel engine radiators.
5. Acknowledgements
The authors would like to express their appreciation to the Islamic Azad University of Abadan Branch for providing financial support.
REFERENCES
- S. U. S. Choi and J. A. Eastman, “Enhancing Thermal Conductivity of Fluids with Nanoparticles,” ASME International Mechanical Congress and Exposition, San Francisco, 12-17 November 1995.
- S. M. Peyghambarzadeh, S. H. Hashemabadi., S. M. Hoseini and M. S. Jamnani, “Experimental Study of Heat Transfer Enhancement Using Water/Ethylene Glycol Based Nanofluids as a New Coolant for Car Radiators,” International Communications in Heat and Mass Transfer, Vol. 38, No. 9, 2011, pp. 1283-1290. doi:10.1016/j.icheatmasstransfer.2011.07.001
- E. Ollivier, J. Bellettre, M. Tazerout and G. C. Roy, “Detection of Knock Occurrence in a Gas SI Engine from a Heat Transfer Analysis,” Energy Conversion and Management, Vol. 47, No. 7-8, 2006, pp. 879-893. doi:10.1016/j.enconman.2005.06.019
- R. S. Vajjha, D. K. Das and P. K. Namburu, “Numerical Study of Fluid Dynamic and Heat Transfer Performance of Al2O3 and CuO Nanofluids in the Flat Tubes of a Radiator,” International Journal of Heat and Fluid Flow, Vol. 31, No. 4, 2010, pp. 613-621. doi:10.1016/j.ijheatfluidflow.2010.02.016
- K. Y. Leong, R. Saidur, T. M. I. Mahlia and Y. H. Yau, “Modeling of Shell and Tube Heat Recovery Exchanger Operated with Nanofluid Based Coolants,” International Journal of Heat and Mass Transfer, Vol. 55, No. 4, 2012, pp. 808-816. doi:10.1016/j.ijheatmasstransfer.2011.10.027
- A. Ijam and R. Saidur, “Nanofluid as a Coolant for Electronic Devices (Cooling of Electronic Devices),” Applied Thermal Engineering, Vol. 32, 2012, pp. 76-82. doi:10.1016/j.applthermaleng.2011.08.032
- M. Saeedinia, M. A. Akhavan-Behabadi and M. Nasr, “Experimental Study on Heat Transfer and Pressure Drop of Nanofluid Flow in a Horizontal Coiled Wire Inserted Tube under Constant Heat Flux,” Experimental Thermal and Fluid Science, Vol. 36, 2012, pp. 158-168. doi:10.1016/j.expthermflusci.2011.09.009
- M. Shafahi, V. Bianco, K. Vafai and O. Manca, “An Investigation of the Thermal Performance of Cylindrical Heat Pipes Using Nanofluids,” International Journal of Heat and Mass Transfer, Vol. 53, No. 1-3, 2010, pp. 376- 383. doi:10.1016/j.ijheatmasstransfer.2009.09.019
- D. G. Charyulu, G. Singh and J. K. Sharma, “Performance Evaluation of a Radiator in a Diesel Engine—A Case Study,” Applied Thermal Engineering, Vol. 19, No. 6, 1999, pp. 625-639. doi:10.1016/S1359-4311(98)00064-7
- K. Y. Leong, R. Saidur, S. N. Kazi and A. H. Mamun, “Performance Investigation of an Automotive Car Radiator Operated with Nanofluid-Based Coolants (Nanofluid as a Coolant in a Radiator),” Applied Thermal Engineering, Vol. 30, No. 17-18, 2010, pp. 2685-2692. doi:10.1016/j.applthermaleng.2010.07.019
- B. C. Pak and Y. I. Cho, “Hydrodynamic and Heat Transfer Study of Dispersed Fluids with Submicron Metallic Oxide Particles,” Experimental Heat Transfer, Vol. 11, No. 2, 1998, pp. 151-170. doi:10.1080/08916159808946559
- Y. Xuan and W. Roetzel, “Conceptions of Heat Transfer Correlation of Nanofluids,” International Journal of Heat and Mass Transfer, Vol. 43, No. 19, 2000, pp. 3701-3707. doi:10.1016/S0017-9310(99)00369-5
- M. Corcione, “Empirical Correlating Equations for Predicting the Effective Thermal Conductivity and Dynamic Viscosity of Nanofluids,” Energy Conversion and Management, Vol. 52, No. 1, 2011, pp. 789-793. doi:10.1016/j.enconman.2010.06.072
- Q. Li and Y. Xuan, “Convective Heat Transfer and Flow Characteristics of Cu-Water Nanofluid,” Science in China Series E: Technological Sciences, Vol. 45, No. 4, 2002, pp. 408-416. doi:10.1360/02ye9047
NOTES
*Corresponding author.

