Open Journal of Biophysics
Vol.05 No.03(2015), Article ID:58364,11 pages
10.4236/ojbiphy.2015.53008
Shifts in Photon Spectral Power Densities within Schumann (7.7 to 7.8 Hz) Values in Microtubules during Complex Magnetic Field Exposures May Reflect an Information Interface with Universal Energies
Michael A. Persinger, Blake T. Dotta, David A. E. Vares, Stanley A. Koren
Quantum Neurobiology Laboratory, Behavioural Neuroscience, Biomolecular Sciences and Human Studies Programs, Laurentian University, Sudbury, Canada
Email: mpersinger@laurentina.ca, bx_dotta@laurentian.ca, dx_vares@laurentian.ca, SKoren@laurentian.ca
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 May 2015; accepted 25 July 2015; published 28 July 2015
ABSTRACT
The specific diameter of microtubules was shown to be a primary solution when magnetic energy was set equal to Casimir energy. To discern if this spatial containment could be foci for information photon emissions were measured from preparations of microtubules (MTs) while they were exposed in sequential 4 min intervals to various patterns of weak magnetic fields whose intensities ranged from 3 to 10 μT. Calculations from the median mass of a tubulin dimer, its summed charges and the applied magnetic field as well as the change in magnetic moment derived from the energy of the hydrogen line when applied to our experimental fields predicted a dynamic shift (Δf) between 0.03 and 0.21 Hz. Spectral power densities (SPD) indicated marked enhancements in photon numbers during periods of magnetic field exposures within the 7.6 to 7.8 Hz increment. The total SPD units for the shift were 10−18 to 10−17 J per s. Five of the eight patterns elicited a split spectrum of power within this range. Separate factor analyses of the SPDs of the serial values that composed the points of the actual field patterns indicated those that evoked the split-spectrum (Δf = 0.05 to 0.13 Hz) displayed significantly higher loadings on the same factor compared to those that did not. If this shift in photon energy reflects a phase modulation of the coherence frequency (8 MHz) of MTs, the increment of energy per MHz frequency would be within the energy of the neutral hydrogen line. These results suggest that the intrinsic structure or information from specific intensity magnetic fields when applied to MTs is reflected in photon energy densities vacillating around the fundamental Schumann Resonance that could be an interface between Casimir and magnetic sources.
Keywords:
Microtubules, Casimir Energy, Magnetic Energy, Photon Emissions, Schumann Resonance, Phase Modulation, Split-Spectrum

1. Introduction
One of the fundamental challenges of biophysics has been to resolve or at least accommodate the probable artificial (or in the very least arbitrary) differentiation between phenomena that have been considered “non-phys- ical” such as consciousness and phenomena with discrete properties such as action potentials or cellular electrodynamics. A series of eloquent philosophical and mathematical arguments by Hameroff and Penrose [1] have suggested the microtubule might be the integrator of the “energy” and the matter (such as protons and electrons) occupying living matter. The potency of the Hameroff and Penrose Orch OR (objective reduction) model [1] is contained within predictions that can be quantified. They have been supported across levels of discourse by Bandyopadhyay and colleagues [2] . If consciousness is “an intrinsic feature of the action of the universe” as postulated by Hameroff and Penrose [1] and it is an emergent process within cells because they are components of the universe [3] according to Mach’s Principle, there should be some primary structure by which this “universal” nature is mediated. If microtubules are central to this process then they or their constituents should exhibit characteristics that reflect fundamental forces. They could be local or non-local. Here we present quantitative solutions and experimental evidence for this proposition.
Bras et al. [4] indicated that the assembled microtubule (MT) exhibits approximately 13 protofilaments which compose a hollow tube whose maximum diameter is 24.6 ± 0.6 nm. The length extends into the micron range with a typical value between 1 and 2 μm although some estimates extend to the length of the neuronal soma (~10 μm). The narrow range of the maximum diameter, that is the coefficient of variation of less than 2% rather than the more typical normal distribution of about 30%, is more consistent with the precision required for tuning rather than broad detection or stochastic distribution of properties. Microtubule structure exhibits dynamic and continuous changes within cells that divide. Although neurons do not divide, except for the unusual adult neurogenesis displayed within specific regions of the hippocampal formation [5] , an intrinsic dynamic process cannot be excluded.
Considering the preponderance of the aromatic amino acids with aggregates of π orbital electrons able to delocalize across discrete spatial regions, photon emissions would be expected even without conspicuous structural degradation or synthesis [6] . If gravitons, an intrinsic component of one of Penrose’s [7] contributions, are indeed “confined photons of the unified non-local field that curves space-time” as suggested by Amoroso [8] , then the critical feature may involve the substrate capacity to emit and receive photons. We have empirical evidence for this possibility [9] . Irena Cosic [10] , the originator of the Resonant Recognition Model for molecular interactions, transformed each of the different amino acids within the tubulin molecule into pseudopotentials. Fast Fourier Transforms of the spectral power densities for the spatial periodicities were then converted to equivalent wavelengths. The assumption is that energy can be transferred as resonance by de-localized electrons. For tubulin the main resonant wavelengths are 2.05 to 2.14 μm, 600 to 615 nm, and 440 to 470 nm. The latter two are within the visible range of detection by conventional digital photomultiplier units. We [11] have verified the validity of Cosic’s concepts by applying filters for specific wavelengths matched for specific molecular pathways [12] .
The metaphor that the “collapse of the wave function” may affect the “dynamics of brain function” and the “emergent properties” such as consciousness [7] has been popular. This “collapse” allows the conditions for the occurrence of specific series of material (matter-related) events. Although it can be considered similar to the matter-wave duality of de Broglie’s earlier concepts [13] , one type of collapse of the wave function suggests that matter can be manifested from virtual particles associated with the vacuum energies and zero point oscillating potentials. In other words, as aptly stated by Bordag et al. [14] , the application of an external (magnetic) field whose boundary conditions depends upon time exhibits the potential to transform vacuum oscillations into real particles. In addition to a Casimir force there is “particle creation”.
If there is a convergence of Casimir energy (Ec):
 (1)
(1)
where ħ is the modified Planck’s constant (1.05 × 10−34 J・s), c is the velocity of light in a vacuum, “a” refers to the width between two Casimir plate-like conditions and m3 is functional volume of the separation between the two plates, and, “magnetic field energy” (Em):
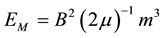 (2)
(2)
where B is the strength of the magnetic field, μ is magnetic permeability (in a vacuum, 4π・10−7 N・A−2) and m3 is the volume within which the field is contained, then when these energies are set equal and the inter-plate distance is calculated from:
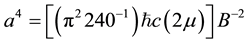 (3)
(3)
the volume component is cancelled and the only variable (non-constant) is B, the strength of the field.
If there is a pervasive component to “consciousness in the universe”, as suggested by Hameroff and Penrose [1] , then one “universal” wave structure and frequency that is ubiquitous would be the neutral hydrogen line. The strength of field required to converge with the energy from the neutral hydrogen line (1.42 GHz) or 9.41 × 10−25 J for the magnetic moments of an electron’s orbit or spin (μB = 9.2740780 × 10−24 J・T−1; μe = 9.2847701 × 10−24 J・T−1, respectively) would be ~0.1 T. With this quantity the 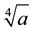 (from equation 3) value is 23.8 nm. This is within the range of the width of the microtubule.
(from equation 3) value is 23.8 nm. This is within the range of the width of the microtubule.
Recent measurements by Dotta et al. [15] indicated that when preparations of microtubules were exposed to 3 to 10 μ Tesla physiologically patterned fields there was an enhancement of spectral power density (SPD) in numbers of photon emissions around 7.7 to 7.8 Hz. Frequency can be derived from (q・kg−1)・B, or, Hz (s−1). The median mass of a tubulin dimer is 55 kD with each monomer carrying 10 units of charge [16] . Hence: [(32 × 10−19 A・s)/(9.13 × 10−23 kg)] (3 × 10−6 T) = Δf = 0.11 Hz. This is remarkably convergent with the power-spectra split measured within the 7.7 to 7.8 Hz range when weak magnetic fields were applied to the microtubule preparations. The shift could be related to a fundamental relationship between charge density, mass and the strength of the applied field. Photons, in the most general sense, have been considered the “process” that mediates forces between the basic units of matter. Contemporary models of physics assume interactions between quarks and leptons are mediated by an exchange of particles or gauge bosons which, within the electromagnetic domain, are photons.
The numbers of photons per second measured by Dotta et al. [15] from preparations of microtubules were directly related to the numbers of microtubules in the experimental condition. The radiant flux density as measured by photomultiplier tubes was in the order of 10−12 W・m−2. This is within the same order of magnitude as the changes in power density from the right side of the heads of participants sitting in hyper-darkness and actively engaging in imagining white light compared to baseline conditions or durations of thinking about “mundane” events [17] . In those studies there was a strong correlation (0.90) between the electroencephalographic power from the left prefrontal lobes (associated with intention) of the participants and the radiant flux density of light emitted from their right caudal skulls. The left prefrontal region is a central node in cerebral networks associated with “intention”, “thinking” and the putative engagement of “free-will” [18] . The patterns of weak magnetic fields that elicited the increased photon emissions during brief exposures have been shown to affect T-type calcium channels in cell membranes [19] as well as produce changes in behaviour that are consistent with long- term potentiation (LTP) after only 30 min of exposure. LTP is considered a fundamental correlate of the transition between acquisition (learning) and memory [20] .
Further fine-structure analyses of the SPD of photon emissions during exposures to temporally-patterned magnetic fields indicated there were two peaks of power at 7.74 and 7.87 Hz, that is a separation Δf = 0.13 Hz. If the applied field induces a change in magnetic moment in an electron orbit by affecting the angular velocity, then the energy for the magnetic field required for the hydrogen line (~0.1 T) would result in the product of that value and the magnetic moment q2・r2・kg−1 where r is the Bohr radius, q is the unit charge and kg is the mass of
an electron, or 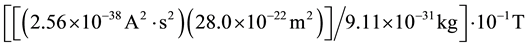 or 7.37 × 10−30 A・m2 or J per T.
or 7.37 × 10−30 A・m2 or J per T.
This also results in a convergent value.
When multiplied by the same minimum value of 3 micro Tesla employed by Dotta et al. [16] the energy is 22.11 × 10−36 J and when divided by Planck’s constant is Δf = 0.03 Hz. If the energy is divided by Planck’s modified constant the result is Δf = 0.21 Hz. This suggests that photon amplitude emissions may match the Schumann fundamental when the appropriate magnetic field is applied and could be “modulated” within the width of the Δf by electromagnetic fields with specific internal temporal structures. The fixed width of the tubulin cylinder could allow Casimir transformations of the magnetic field strength from the hydrogen line energy which is mediated through direct effects of induced magnetic moment from a discrete change in angular velocity.
Here we report evidence that different patterns of magnetic fields produce different shifts in the split spectra around the fundamental Schumann frequency in microtubule preparations and that these interesting dimers may serve as an interface between fundamental forces and essential biological functions including the more ephemeral features of consciousness which is strongly correlated with electromagnetic fields with a centroid ~40 Hz. In addition we present results that strongly suggest that information (as different electromagnetic temporal patterns) relevant to cell function could be mediated through or strongly correlated with the configuration of the split in Schumann-like fundamentals in the spectral power density of the photon emissions from MTs during brief field exposures.
2. Methods and Materials
Plates of ~5 × 105 B16-BL6 mouse melanoma cells were prepared so that microtubules (MTs) and the cell nucleus primarily remained in the dish [6] . The incubated (37˚) plates of microtubule preparations were then removed to room temperature within a 13 m3 Faraday Room where a hyperdark environment (10−11 W・m−2) was maintained. Each plate was placed on top of the aperture of a digital PMT (Model DM0090C from SENS-TECH, LTD). The plate and the sensor for the PMT were positioned between two containers within which the solenoids were contained. A diagram of the experimental arrangement is shown in Figure 1 that was identical to those reported for other experiments in which photon emissions in response to weak patterned magnetic fields had been measured [6] [21] .
The magnetic fields were generated from special software by which a series of numbers between 0 and 256 were transformed to −5 to +5 V where 127 = 0 V through a custom-constructed digital to analogue converter (DAC). The point durations (presentation time) for each number was primarily 1 ms although some patterns involved 3 ms (there was no difference in effect). The output was connected to four pairs of solenoids arranged in a quasi-circle within the containers. The circuit was constructed so that at any given time only one pair (one in the left and one in the right container) was activated for 0.5 s, or 2 s for one rotation.
Eight programmable patterns, shown in Figure 2, were presented for 4 min each in a sequence with intermittent 4 min periods of no magnetic fields to plates of MTs. For any given experiment not more than 5 field patterns from Figure 2 were presented along with the intermittent 4 min intervals with no field presentations. Results of previous experiments indicated this duration was sufficient to elicit clear photon emissions when the fields were present with intensities between 3 and 10 μT.
Figure 1. Diagram of the experimental arrangement indicating the placement of the plates of microtubule (MT) preparations over the aperture of the PMT and the placement of the EMF devices.
Figure 2. The temporal shapes of the patterns employed in the present study to affect the Spectral Power Density of the photon emissions from microtubule preparations. Top (Linda- gene), second row left (LTP), second row right (negative polarity, third row left (burstx), third row right (Thomas), fourth row left (40 Hz sine wave, and fourth row right (Fibonacci). The 8th pattern (Schumann variant) is not shown; it was a square wave 7 Hz pattern.
Measurement and Analysis Procedures
During the successive 4 min periods of either field (one of the patterns in Figure 2) or no field intervals the numbers of photons emitted from the MTs were measured once every 20 ms (50 Hz) which was the upper limit for the software for collection for the equipment. The monitoring equipment as well as the computer that allowed the changes in programming to generate the different field patterns was outside of the closed exposure chamber. The data were then loaded into SPSS-PC 16 programs and analyzed for total photon counts per second for each 4 min exposure. In addition, spectral analyses were completed for each 4 min (240 s) segment in order to discern Spectral Power Densities (SPD). In previous experiments we had found that although the absolute numbers of photons may not increase with some types of patterned magnetic fields there was a robust shift in the amplitude distributions (reflected as SPD) of the photon emissions over the frequency range during the exposures.
3. Results
The first conspicuous effect measured from MTs during serial exposures of 4 min to the various magnetic field configurations was the diminished responsiveness over time. The effect occurred regardless of the order of the presentations of the patterned magnetic fields which were always counterbalanced for presentation. An example is shown in Figure 3. Each trial was about 4 min.
The inflection point for the diminished photon emissions was about trial 3 and 4 which was about 45 min after removal from incubation. The first measurement (about 30 min after removal from incubation) was 3 photons
Figure 3. Vertical axis indicated the photon counts from dishes of micro- tubule preparations per 20 ms as a function of the successive 4 min trials. Vertical bars indicate standard deviation.
per 20 ms or 150 photons per s. The value at trial 11 was similar to that which was measured from the beginning of the experiment when medium only was present in the plates and was similar to the dark counts for this particular instrument. Assuming the energy associated with the peak wavelength of the PMT (5 × 10−19 J), the power would be 7.5 × 10−17 J per s (Watts). Because the area of the aperture was 10−4 m2 the radiant flux density (irradiance) of the MTs would be about 7.5 × 10−13 W・m−2 which is within the range of our typical measurements.
There was no statistically significant difference between the mean photon counts measured from the MTs as a function of the different patterns. The increased amplitude of the spectral power density (SPD) from the applied fields was evident as well as the “split” or bimodal variation of the peak power within the 7.6 to 7.8 Hz band. The major peak was between 7.75 and 7.85 Hz. Each SPD unit was equivalent to about 0.28 photon counts per s. The magnitude for the split for the elevated SPD above the conditions when no field or a field that was not effective was present varied between 10 and 40 SPD units. This would be equivalent to the increased availability of energy of between 1.4 and 5.6 × 10−18 J per s per 0.1 Hz due to the presence of the appropriately patterned magnetic field for only 4 min. This separation occurred (Δf indicated in parentheses) only for the following patterns (Figure 2): (Thomas: 0.13 Hz), LTP (0.13 Hz), Lindagene (0.05 Hz), pure 40 Hz sine wave oscillations (0.06 Hz) and negative polarity sine-wave oscillations (0.08 Hz). The other patterns (Schumann variant, Fibonacci, and Burstx) did not elicit a significant separation of SPD peaks within this band. There were no statistically significant correlations (Spearman rho) between the numbers of original points in the patterns and the magnitude of the shifts in Δf.
In order to discern the physical features of the patterns of the fields that produced the significant split in the 7.7 Hz to 7.8 Hz SPD for numbers of photons compared to those that did not spectral analyses were completed for the values that defined each of the 8 patterns (DAC files) from which the magnetic fields were created. Again each file was composed of a column of numbers between 0 and 256. Because the original number fields were different lengths and spectral analyses require equal sample sizes the shorter files were systematically repeated until they reach the value of the longest field (Lindagene) which was 9999 points. We know that the lowest spectral frequencies distort the effects because of their magnitudes. Consequently, factor analyses were completed on successive 0.01 increments of spectral frequency (temporal) units for >0.01 units.
The conspicuous relationship was apparent at >0.03 spectral frequency or above 30 Hz (assuming 1 ms point durations). The non-rotated factor scores for the largest factor (of 3 factors) that explained 19% of the variance (eigen value = 1.5) were obtained for each of the 8 patterns. The means and standard deviation for the factor scores for the five patterns that produced the split in the photon emission power spectra between 7.7 and 7.8 Hz were 0.52 and 0.23, respectively. The mean and standard deviation for the three patterns that did not produce this separation were 0.14 and 0.04. There was no overlap in values between the two groups. The differences were strongly statistically significant [F (1, 6) = 14.26, p < 0.01; 70% variance explained].
We discerned the relationship between the factor scores upon which the different patterned magnetic fields loaded differentially depending upon their capacity to elicit the splitting of SPD of the photon emission from MTs and the intrinsic frequency. To obtain this solution the factor score was calculated by adding the products for the square of each of the loading factors and the spectral values for the internal variation of the values that defined the pattern for each of the 8 patterns for the range between 30 and 40 Hz. This interval was selected because it displayed the greatest variability and most of the power compared to >40 Hz. The spectral pattern of the log10 of these values as a function of frequency revealed a conspicuous periodicity.
Based upon our assumption that the complex interaction between electromagnetic fields associated with consciousness and universal energies (mediated through photons) occur within the domains of second derivatives, that is rates of rates of change [22] , we performed a second order spectral analysis. It was completed as a function of the rate of change of frequency. The results are shown in Figure 4. The recondite second order derivative of frequency or shift in power frequency peaked within the 0.03 and 0.11 ΔHz band. Again this reflects the occluded temporal properties of the internal structures of the magnetic fields (which we suspect are the analogues to inner dot products, a first step to engaging Hilbert space) that produced the shift (ΔHz) in the photon SPD between 7.7 to 7.8 Hz.
4. Discussion
If the specific width of the tubulin dimer organization of the microtubules relates to a fundamental property that is reflected at the level of the interaction between Casimir energies and magnetic energies as derived in the Introduction, then there should be convergence of other energies that have universal features. The average numbers of photons emitted from the preparations of microtubules (MTs) was about 50 photons per s. Assuming each photon was ~5 × 10−19 J (based upon the peak sensitivity of the PMT), the power would have been 2.5 × 10−17 W. Given the aperture was 10−4 m2, the radiant flux density would have been about 0.3 × 10−12 W・m−2 which is well within the range measured for a variety of tissue preparations such as hippocampal slices [23] as well as from the active human brain [17] .
More salient to the present approach is the quantitative amount of energy per microtubule dimer. Assuming the equivalent of 106 cell equivalents of microtubule preparations within the area of the aperture within the dishes and about 100 microtubules (a typical average) per cell, the average energy per microtubule would be ~2.5 × 10−25 J. When divided by Planck’s modified constant, 1.05 × 10−34 J・s, the resulting frequency is within a few percent of the frequency for the neutral hydrogen line (1.42 × 109 Hz). This ubiquitous and pervasive frequency can be measured across the universe. Hence this particular flux power density from these structures
Figure 4. Spectral power density of primary factor for spectral densities as a function of the derivative of Hz (shift in frequency) within the 30 to 40 Hz range of the factor scores based upon the internal structure of the applied magnetic fields. within the 30 to 40 Hz range of the factor scores based upon the internal structure of the applied magnetic fields.
within cells would have the potential to intercalate with the frequency associated with hydrogen lines. This could include juxtaposition for local effects and superposition for non-local effects [13] .
The convergence of the specific diameter of the microtubule with the solution between the Casimir and magnetic energies and the specific enhancement of spectral power densities with the Schumann Resonance (7.7 to 7.8 Hz) for photons emitted from MTs when weak fields were applied would be compatible with the concept that the MTs are interfaces of universal energies. Our results are consistent with the (but not the only) possibility that these interactions are mediated through the spherical wave guide between the earth and ionosphere through which the fundamental frequency of the Schumann Resonance is generated [24] . The Schumann Resonance was very likely to have been present during the Precambrian abiogenesis [25] when lightning strikes (which are the energetic source of the resonances) contributed to the formation of amino acids from atmospheric constituents. Such convergence would also be compatible with Hameroff and Penrose [1] concept that “consciousness” is a property or action within the universe.
If the Schumann resonance, particularly the fundamental frequency, has been present since the beginning of biophysical systems on this planet an intrinsic residual would be expected. Consequently the ubiquitous presence of the theta rhythm (4 to 8 Hz) pattern within the hippocampal formations of mammals upon which a 40 Hz ripple is superimposed and transmitted through the cerebral cortices would facilitate a coupling between the capacity to represent information (i.e., memory) and cerebral cortical consciousness [26] [27] . One of the implications of such coupling between hippocampal activity and earth-ionospheric activity is that interaction could occur.
Saroka and Persinger [28] while measuring the quantitative electroencephalographic power of human volunteers discerned a superimposition of the Schumann fundamental of 7 - 8 Hz as well as the harmonics, primarily 14 - 15 Hz, 20 - 21 Hz and occasionally 26 to 27 Hz, within the electroencephalographic profile. These brief (~0.3 s about two times per min) displays were coherent in real time with the power fluctuations in the Schumann Resonance as measured directly in Italy and locally. The strong correlations between our local station (in Sudbury, Ontario) and another more than 3000 km away and their values with spectra power densities from human electroencephalographic activity suggest that changes within the spherical waveguide anywhere over the earth’s surface could be correlated with discrete, brief power changes (in the order of 1 to 2 μV) within the human cerebral cortices. When diffusivity is included, derived from the magnetic permeability of space and the typical resistivity of aqueous extracellular cerebral environment (~2 Ω・m) the magnetic field strength would be around 2 pT. This is the average amplitude of the Schumann Resonance [24] .
The mechanism by which such coupling could occur has been isolated to the right hemisphere, specifically within the right parahippocampal region which is known to interface and to interact within the entire cerebral cortical manifold [29] . Mulligan and Persinger [30] showed that the right hemisphere is also the region of the brain that responds maximally to weak geomagnetic activity and its simulation in experimental settings. The results of our experiments here indicate that the microtubule, an integral component of neurons and a major factor in Hameroff and Penrose’s model for cognitive function [1] , generate 7 - 8 Hz fluctuations in the spectral power of numbers of photons per s. The flux densities of these emitted photons are within the range expected to be sources of “information” within and without cells [31] [32] .
Although the diminishment of bulk photon emissions as a function of time since the removal form the optimal temperature (37˚C) would be expected (Figure 3) if these quanta were related to information between MTs or cells, the quantitative values might be revealing. The asymptote for the habituation occurred around 45 min. According to a general estimate for time to habituation [33] , as inferred by the inflection latency (τ) of any system which is:
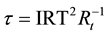 (4)
(4)
where IRT is the time between responses and Rt is the duration of the elemental unit. For 2.7 × 103 s (45 min) with an IRT of 25 ms (the duration of our photon measurement as well as the intrinsic repetition rate of the electromagneto-dynamic 40 Hz gamma synchrony component of consciousness [34] , an important feature of the Hameroff and Penrose hypothesis [1] ), the value would be the equivalent of about 4 to 5 MHz. This is within the range of the 8 MHz coherence measured in microtubules by Pokorny [35] .
That photon emission would be expected from microtubules is compatible with the original concepts of Cosic’s Resonant Recognition Model [36] . This model focuses upon the spatial periodicities (of frequencies) within the energy distributions of delocalized electrons along a sequence of amino acids, that is, a protein. According to Cosic the movements of these delocalized electrons along the “protein backbone” reveal as energetic resonance that determines the function of molecules. The movement of electrons produces an electromagnetic field with very specific characteristics that are primarily within the infrared and ultraviolet range. Cosic, Lazar and Cosic [10] showed that tubulin exhibits very specific resonant frequencies with peaks within the 2.05 to 2.14 μm (infrared), 440 to 470 nm (ultraviolet interface with the visible wavelength boundary) and 600 - 615 nm. The PMT that we employed is maximally sensitive around the 450 nm range.
The infra-red peak is particularly important from a fundamental physics perspective in light of Bohr’s solution [37] . According to his seminal concepts the frequency and hence magnitude of the quantum involved if one nucleus is removed from another as a standing space, reflected as λ, can be derived from:
 (5)
(5)
where M is the mass of the proton, m is the mass of the electron and ωo = 6.2 × 1015 Hz. The inverse wavelength value for the frequency is λr = 1.57 μm. In other words one of the Cosic solutions for photon energy for tubulin converges with the wavelength corresponding to the displacement when one proton is removed from the context of another. This is a major feature of both this particle’s movement across hydronium ions and is a strong contributor to Grotthuss chains. We have shown experimentally [38] that the mediation of applied photons through living human cerebral tissue is consistent with proton movements typical of those responsible for the hydronium ion and shifts in pH. These proton movements may be a primary process by which embedded magnetic fields from external sources mediate their effects within aqueous solutions [39] [40] .
The results of this experiment confirm those from previous research [6] that demonstrated a shift in spectral power densities of spontaneous photon (biophoton) emissions from preparations of microtubules from cells. One of the major peaks in SPD occurred within the band that has been associated with the Schumann Resonance. What we found is that different patterns of the applied magnetic fields at intensities sufficient to produce a small but predictable shift in frequencies produced specific patterns in the “splitting” of this Schumann-like profile. Because all patterns did not produce the significant bimodal separation of spectral power within the Schumann fundamental frequency the effect was not likely due to simply the application of a magnetic field per se.
Instead the presence or absence of the “splitting” in the 7.7 to 7.8 Hz enhancement of power density of photon emissions from the MTs was related to the quantitative loading of the spectral power densities above 30 Hz of the actual power distributions within the structure of the applied magnetic fields loading on the same shared source of variance (factor). The difference in the magnitude of the loading coefficients on the factor for those patterns that elicited the split in SPD for photon emissions within the 7.7 to 7.8 Hz band and those that did not was equivalent to a correlation coefficient of 0.83. The spectral pattern of this factor was most effective within the 30 to 40 Hz range. The derivative or rate of change of the frequency, as shown in Figure 4, for the intrinsic structural complexity within the applied fields was within the 0.03 to 0.11 Hz range.
This convergence strongly suggests that the apparent “shape” of the applied magnetic field is less important than its property of temporal (derivative) shifting within a specific narrow band. We have also shown experimentally that the gross visual pattern of complex magnetic fields that appear to be quite dissimilar but share factor structures or similar spectral power densities produce almost identical suppression of malignant cell growth in cell culture [41] . From this perspective it may not be spurious that the typical splitting of the actual Schumann fundamental within the earth-ionosphere waveguide is also within the tenths of a Hz range although the actual band of the fundamental is ~2 Hz [24] .
On the bases of our current theoretical conceptions and several anecdotal measurements and observations under special conditions the Δfs may not have been simple displacements such as a shift in polarization. We suggest that the narrow range of shift, Δf = 0.05 to 0.13 Hz, within the 7.7 to 7.85 Hz interval was not static but could have reflected a phase modulation of this Schumann fundamental within the MHz range. Interestingly Streltsov et al. [42] experimentally induced large amplitude 7.8 to 8 Hz waves when the ionosphere was penetrated by 3.2 to 4.57 MHz radiation and correlative electric fields > 5 mV・m−1. The amplification occurred in successive 0.2 Hz increments of 7.4, 7.6, 7.8 and 8.0 Hz.
Although most phase modulation systems involve shifting a faster frequency carrier by a lower frequency, a spherical-wave guide source that encompasses the earth (a sphere, with a second derivative of 8π) and hence is an inclusive surface area antenna may shift the parameters. If this approach is valid then the 8 MHz coherence measured in microtubules by Pokorny [35] is applicable. This would mean that about 1 Mbyte of information per s could be processed within this phase modulation within a prototypical array of microtubules.
For our measurements the SPD equivalent in raw photon counts within the elevated 7.7 to 7.8 Hz band that was associated with the split by the specific magnetic fields was about 0.28 photons per SPD unit. The magnitude of the enhanced SPD in the split band was between 10 and 40 SPDs or between 1.4 and 5.6 × 10−18 J per s of energy. If this were a coherent phase modulation associated with 8 MHz, then there would be about 0.7 × 10−24 J per unit Hz for 10 MHz. When divided by Planck’s constant the equivalent frequency is convergent with 1.4 × 109 Hz, the neutral hydrogen line. There is also sufficient energy for involvement of the dissipation of energy from or to entropy as defined by the Landauer Limit which is defined as ln2 kT where k is the Boltzmann constant and T is temperature. From the temperature of the microtubules the threshold would be about 2.96 × 10−21 J. This would be equivalent to the capacity for about 1000 bits per second for MTs from about 105 cells.
Acknowledgements
We thank Dr. W. E. Bosarge, Jr., CEO of Capital Technologies, Inc. for his support of innovative research. Professor Kevin Saroka’s experimentation with complexity and Dr. Carly Buckner’s preparation of MTs were appreciated.
Cite this paper
Michael A.Persinger,Blake T.Dotta,David A. E.Vares,Stanley A.Koren, (2015) Shifts in Photon Spectral Power Densities within Schumann (7.7 to 7.8 Hz) Values in Microtubules during Complex Magnetic Field Exposures May Reflect an Information Interface with Universal Energies. Open Journal of Biophysics,05,84-95. doi: 10.4236/ojbiphy.2015.53008
References
- 1. Hameroff, S. and Penrose, R. (2014) Consciousness in the Universe: A Review of the “Orch OR” Theory. Physics of Life Reviews, 11, 39-78. http://dx.doi.org/10.1016/j.plrev.2013.08.002
- 2. Sahu, S., Ghosh, S., Fujita, D. and Bandyopadhyay, A. (2014) Live Visualizations of Single Isolated Tubulin Protein Self-Assembly via Tunneling Current: An Effect of Electromagnetic Pumping during Spontaneous Growth of Molecule. Scientific Reports, 4, Article Number: 7303.
http://dx.doi.org/10.1038/srep07303 - 3. Persinger, M.A. and Lafrenie, R.M. (2014) The Cancer Cell Plasma Membrane Potentials as Energetic Equivalents to Astrophysical Properties. International Letters of Chemistry, Physics and Astronomy, 17, 67-77. http://dx.doi.org/10.18052/www.scipress.com/ILCPA.36.67
- 4. Bras, W., Torbet, J., Diakum, G.L., Rikken, J.A. and Diaz, J.F. (2014) The Diamagnetic Susceptibility of the Tubulin Dimer. Journal of Biophysics, 2014, Article ID: 985082.
http://dx.doi.org/10.1155/2014/985082 - 5. Eriksson, P.S., Perfilieva, E., Bjork-Eriksson, T., Alborn, A.-M., Nordborg, C., Peterson, D.A. and Gage, F.H. (1998) Neurogenesis in the Adult Human Hippocampus. Nature Medicine, 4, 1313-1317.
http://dx.doi.org/10.1038/3305 - 6. Dotta, B.T., Vares, D.E.A., Buckner, C.A., Lafrenie, R.M. and Persinger, M.A. (2014) Magnetic Field Configurations Corresponding to Electric Field Patterns that Evoke Long-Term Potentiation Shift Power Spectra of Light Emissions from Microtubules from Non-Neural Cells. Open Journal of Biophysics, 4, 112-118. http://dx.doi.org/10.4236/ojbiphy.2014.44013
- 7. Penrose, R. (1989) The Emperor’s New Mind: Concerning Computers, Minds and the Laws of Physics. Oxford University Press, Oxford.
- 8. Amoroso, R.L. (1997) A Brief Introduction to Noetic Field Theory: The Quantization of the Mind. Brain and Cognition, Proceedings ECPD Symposium, Belgrade, 22-23 September 1997, 297-302.
- 9. Dotta, B.T., Buckner, C.A., Lafrenie, R.M. and Persinger, M.A. (2011) Photon Emissions from Human Brain and Cell Cultures Exposed to Distally Rotating Magnetic Fields Shared by Separate Light-Stimulated Brains and Cells. Brain Research, 388, 77-88.
http://dx.doi.org/10.1016/j.brainres.2011.03.001 - 10. Cosic, K., Lazar, K. and Cosic, D. (2014) Prediction of Tubulin Resonant Frequencies Using the Resonant Recognition Model (RRM). IEEE Transactions on NanoBioscience, 14, 491-496.
- 11. Karbowski, L.M., Murugan, N.J. and Persinger, M.A. (2015) Novel Cosic Resonance (Standing Wave) Solutions for Components of JAK-STAT Cellular Signaling Pathways: A Convergence of Spectral Density Profiles. FEBS Open Bio, 5, 245-250. http://dx.doi.org/10.1016/j.fob.2015.03.004
- 12. Dotta, B.T., Murugan, N.J., Karbowski, L.M., Lafrenie, R.M. and Persinger, M.A. (2014) Shifting Wavelengths of Ultraweak Photon Emissions from Dying Melanoma Cells: Their Chemical Enhancement and Blocking are Predicted by Cosic’s Theory of Resonant Recognition Model for Macromolecules. Naturwissenchaften, 101, 87-94. http://dx.doi.org/10.1007/s00114-013-1133-3
- 13. Aczel, A.D. (2002) Entanglement: The Great Mystery of Physics. Raincoast, Vancouver.
- 14. Bordag, M., Mohideen, U. and Mostepanenko, V.M. (2001) New Developments in the Casimir Effect. Physics Reports, 353, 1-205. http://dx.doi.org/10.1016/S0370-1573(01)00015-1
- 15. Dotta, B.T., Vares, D.A.E. and Persinger, M.A. (2015) Spectral Power Densities of the Fundamental Schumann Resonance Are Enhanced in Microtubule Preparations Exposed to Temporally Patterned Weak Magnetic Fields. (in submission)
- 16. Raviv, U., Needleman, D.J., Ewert, K.K. and Safinya, C.R. (2007) Hierarchical Bionanotubules Formed by the Self-Assembly of Microtubules with Cationic Membranes and Polypeptides. Journal of Applied Crystallography, 40, s83-s87. http://dx.doi.org/10.1107/S0021889806051995
- 17. Dotta, B.T., Saroka, K.S. and Persinger, M.A. (2012) Increased Photon Emission from the Head While Imaging Light in the Dark Is Correlated with Changes in Electroencephalographic Power: Support for Bokkon’s Biophoton Hypothesis. Neuroscience Letters, 513, 151-154.
http://dx.doi.org/10.1016/j.neulet.2012.02.021 - 18. Reniers, R.L.E.P., Corcoran, R., Vollm, B.A. Mashru, A., Howard, R. and Liddle, P.F. (2012) Moral Decision-Making, Theory of Mind, Empathy and the Default Mode Network. Biological Psychology, 90, 202-210. http://dx.doi.org/10.1016/j.biopsycho.2012.03.009
- 19. Buckner, C.A., Buckner, A.L., Koren, S.A., Persinger, M.A. and Lafrenie, R.M. (2015) Inhibition of Cancer Cell Growth by Exposure to a Specific Time-Varying Electromagnetic Field Involves T-Type Calcium Channels. PloS ONE, 10, e0124136. http://dx.doi.org/10.1371/journal.pone.0124136
- 20. Mach, Q.M. and Persinger, M.A. (2009) Behavioural Changes with Brief Exposures to Weak Magnetic Fields Patterned to Simulate Long-Term Potentiation. Brain Research, 1261, 45-53.
http://dx.doi.org/10.1016/j.brainres.2009.01.002 - 21. Dotta, B.T., Buckner, C.A., Cameron, D., Lafrenie, R.F. and Persinger, M.A. (2011) Biophoton Emission from Cell Cultures: Biochemical Evidence for the Plasma Membrane as the Primary Source. General Physiology and Biophysics, 30, 301-309.
- 22. Tsang, E.W., Koren, S.A. and Persinger, M.A. (2004) Power Increases within the Gamma Range Over the Frontal and Occipital Regions during Acute Exposures to Cerebrally Counterclockwise Rotating Magnetic Fields with Specific Derivatives of Change. International Journal of Neuroscience, 114, 1183-1193.
http://dx.doi.org/10.1080/00207450490475643 - 23. Isojima, Y., Isoshima, T., Nagai, K., Kikuchi, K. and Nakagawa, H. (1995) Ultraweak Biochemiluminescence Detected from Rat Hippocampal Slices. NeuroReport, 6, 658-660.
http://dx.doi.org/10.1097/00001756-199503000-00018 - 24. Nickolaenko, A. and Hayakawa, M. (2014) Schumann Resonance for Tyros: Essentials of Global Electromagnetic Resonance in the Earth-Ionospheric Cavity. Springer, New York.
http://dx.doi.org/10.1007/978-4-431-54358-9 - 25. Graf, F.E. and Cole, E.R. (1974) Precambrian ELF and Abiogenesis. In: Persinger, M.A., Ed., ELF and VLF Electromagnetic Field Effects, Plenum Press, New York, 243-273.
- 26. Buzsaki, G. (2002) Theta Oscillations in the Hippocampus. Neuron, 33, 325-340.
http://dx.doi.org/10.1016/S0896-6273(02)00586-X - 27. Angel, A. and Klink, R. (1993) Differential Responsiveness of Stellate and Pyramidal-Like Cells of the Medial Entorhinal Cortex: Layer II. Journal of Neurophysiology, 70, 128-143.
- 28. Saroka, K.S. and Persinger, M.A. (2014) Quantitative Evidence for Direct Effects between Earth-Ionosphere Schumann Resonances and Human Cerebral Cortical Activity. International Letters of Chemistry, Physics and Astronomy, 20, 166-194.
http://dx.doi.org/10.18052/www.scipress.com/ILCPA.39.166 - 29. Persinger, M.A. and Saroka, K.S. (2014) Quantitative Support for Convergence of Intrinsic Energies from Applied Magnetic Fields and “Noise” Fluctuations of Newton’s Gravitational Value within the Human Brain. International Letters of Chemistry, Physics and Astronomy, 19, 181-190.
http://dx.doi.org/10.18052/www.scipress.com/ILCPA.38.181 - 30. Mulligan, B.P. and Persinger, M.A. (2012) Experimental Simulation of the Effects of Sudden Increases in Geomagnetic Activity upon Quantitative Measures of Human Brain Activity. Neuroscience Letters, 516, 54-56. http://dx.doi.org/10.1016/j.neulet.2012.03.054
- 31. Fels, D. (2009) Cellular Communication through Light. PloS ONE, 4, e5086.
http://dx.doi.org/10.1371/journal.pone.0005086 - 32. Trushin, M.V. (2004) Light-Mediated Conversation among Microorganisms. Microbiological Research, 159, 1-10. http://dx.doi.org/10.1016/j.micres.2003.11.001
- 33. Persinger, M.A. (1979) A First Order Approximation of Satiation Time: IRT2/Rt. Perceptual and Motor Skills, 49, 649-650. http://dx.doi.org/10.2466/pms.1979.49.2.649
- 34. Llinas, R.R. and de Pare, D. (1991) Of Dreaming and Wakefulness. Neuroscience, 44, 521-535.
http://dx.doi.org/10.1016/0306-4522(91)90075-Y - 35. Pokorny, J. (2004) Excitation of Vibrations in Microtubules in Living Cells. Bioelectrochemistry, 63, 321-326. http://dx.doi.org/10.1016/j.bioelechem.2003.09.028
- 36. Cosic, I. (1994) Macromolecular Bioactivity: Is It Resonant Interaction between Macromolecules? Theory and Applications. IEEE Transactions on Biomedical Engineering, 41, 1101-1114.
http://dx.doi.org/10.1109/10.335859 - 37. Lewis, W.C. (1921) A System of Physical Chemistry. Longmans, Green and Co., London.
- 38. Persinger, M.A., Dotta, B.T. and Saroka, K.S. (2013) Bright Light Transmits through the Brain: Measurement of Photon Emissions and Frequency-Dependent Modulation of Spectral Electroencephalographic Power. World Journal of Neuroscience, 3, 10-16.
http://dx.doi.org/10.4236/wjns.2013.31002 - 39. Murugan, N.J., Karbowski, L.M. and Persinger, M.A. (2014) Serial pH Increments (20 to 40 Milliseconds) in Water during Exposures to Weak, Physiologically Patterned Magnetic Fields: Implications for Consciousness. Water, 6, 45-60.
- 40. Murugan, N.J., Karbowski, L.M., Lafrenie, R.M. and Persinger, M.A. (2015) Maintained Exposure to Spring Water But Not Double Distilled Water in Darkness and Thixotropic Conditions to Weak (~1 μT) Temporally Patterned Magnetic Fields Shift Photon Spectroscopic Wavelengths: Effects of Different Shielding. Journal of Biophysical Chemistry, 6, 14-28. http://dx.doi.org/10.4236/jbpc.2015.61002
- 41. Karbowski, L.M., Harribance, S.L., Buckner, C.A., Mulligan, B.P., Koren, S.A. Lafrenie, R.M. and Persinger, M.A. (2012) Digitized Quantitative Electroencephalographic Patterns Applied as Magnetic Fields Inhibit Melanoma Cell Proliferation in Culture. Neuroscience Letters, 523, 131-134.
http://dx.doi.org/10.1016/j.neulet.2012.06.059 - 42. Streltsov, A.V., Guido, T., Tulegenov, B., Lanenski, J. and Chang, C.-L. (2014) Artificial Excitement of ELF Waves with Frequency of Schuman Resonance. Journal of Atmospheric and Solar-Terrestrial Physics, 119, 110-115. http://dx.doi.org/10.1016/j.jastp.2014.07.004





