Open Journal of Biophysics
Vol.3 No.4(2013), Article ID:38150,5 pages DOI:10.4236/ojbiphy.2013.34027
An Influence of the Noise on the Imaging Algorithm in the Electrical Impedance Tomography*
1Faculty of Physics and Electronic Engineering, Xianyang Normal University, Xianyang, China
2School of Highway, Chang’an University, Xi’an, China
3Department of Civil, Environmental and Geomatic Engineering, University College London, London, UK
Email: xdzhxy@163.com
Copyright © 2013 Hui Zhang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 24, 2013; revised August 31, 2013; accepted September 16, 2013
Keywords: MPSO-MNR Algorithm; Signal-To-Noise Ratio; Objective Function; EIT
ABSTRACT
Electrical impedance tomography (EIT) reconstructs the internal impedance distribution of the body from electrical measurements on body surface. The algorithm research is one of the main problems of the EIT. This paper presents the MPSO-MNR Algorithm, which is formed by combining the Modified Particle Swarm Optimization (MPSO) with Modified Newton-Raphson algorithm (MNR), gives the reconstruction results of certain configurations and analyzes the influence of the noise on the MPSO-MNR algorithm in the EIT. The numerical results show that the MPSO-MNR algorithm can reconstruct the resistivity distribution within the certain iterations. With the moving of the target to the centre of 2-D solution domain and the increase of noise, the border of the reconstruction objects becomes vague, and the fitness value and the total error increase gradually.
1. Introduction
Electrical impedance tomography (EIT) is a non-invasive imaging technique, which aims to reconstruct images of internal electrical property (conductivity, permittivity and permeability in some high-frequency non-medical applications) distributions and variations by making electrical measurements on the body’s surface [1]. The imaging methods are classified as dynamic or static imaging form. The static imaging method reconstructs the electrical parameter distribution in the solution domain. Static EIT imaging problem is solved by transforming the problem into an objective function, and using the iterative method to achieve the electrical parameter reconstruction [2,3], because it is the nonlinear inverse problem.
Algorithm research is one of the main problems of the static EIT. Based on deterministic and stochastic optimizers, many static EIT algorithms have been proposed [2,3], such as Modified Newton-Raphson (MNR) algorithm [4], Double Constraint Method (DCM), Layer Stripping Method (LSM), the reconstruction algorithms based on the Particle Swarm Optimization (PSO) [5-7], Genetic algorithm (GA) [8] etc. In recent years, some synthetic algorithms have been proposed, for example, Homotopy-Modified Newton-Raphson algorithm (HMNR) [1], and MPSO-MNR algorithm [9]. From a computational point-of-view, the deterministic techniques (e.g., MNR methods) are very attractive, for example, MNR algorithm has the fast convergence speed and the calibration nature. However, the starting trial solution should be closed enough to the “actual” solution. The use of the stochastic genetic algorithms (GA) would, in principle, avoid such a circumstance. But in the GA, various numerical parameters must be carefully calibrated and customized to the application. PSO is a robust stochastic algorithm which overcomes GA’s drawbacks [10]. Taking into account the features of PSO and MNR, we combine the advantages of MPSO and MNR algorithm to form the MPSO-MNR algorithm. Its performance and influence of the noise on the PSO-MNR are analyzed and discussed in this paper.
The paper is structured as follows. After the introduction of the mathematical model of the EIT (Section 2), Section 3 presents the MPSO-MNR algorithm, Section 4 presents a case study to show the MPSO-MNR algorithm performance and the influence of the noise on the reconstruction results. Section 5 provides some concluding remarks.
2. Mathematical Model
The principle of operation of EIT is shown in Figure 1, where the electrical current is injected according to the certain driven pattern, and the electrical potential of the body’s surface is measured by the electrodes. Based on electromagnetic theory, when an injected electrical current is at a sufficiently low frequency, the EIT problem can be treated as a quasi-static problem. Given the resistivity distribution inside the body, the potential  satisfies the Laplace’s equation and the boundary conditions as follows [11]:
satisfies the Laplace’s equation and the boundary conditions as follows [11]:
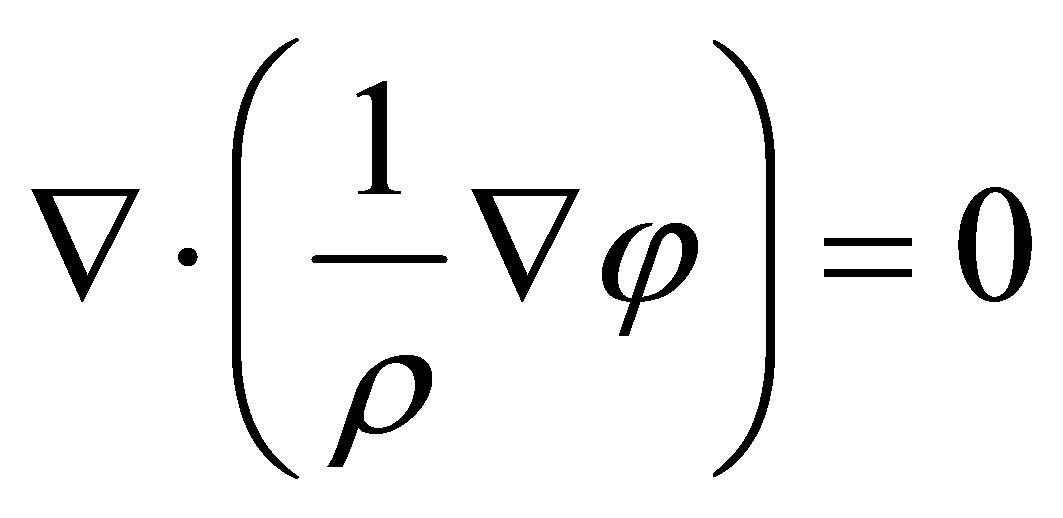 in solution domain, (1)
in solution domain, (1)
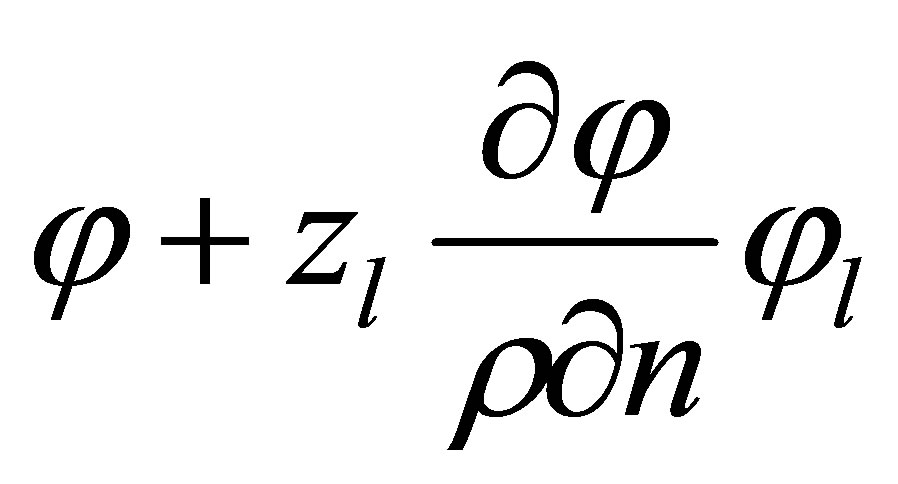 at measuring electrodes, (2)
at measuring electrodes, (2)
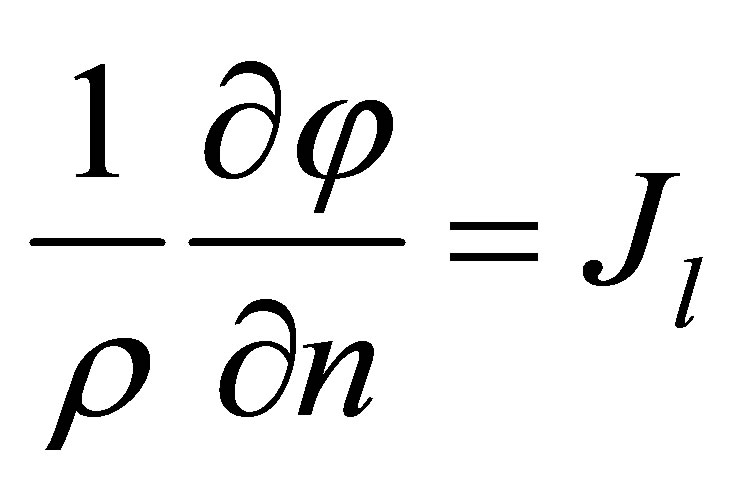 at the current injection electrodes, (3)
at the current injection electrodes, (3)
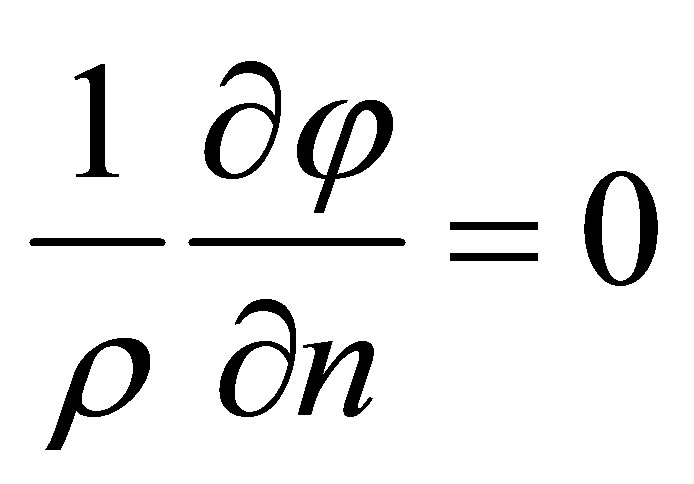 at no-injection electrodes. (4)
at no-injection electrodes. (4)
where 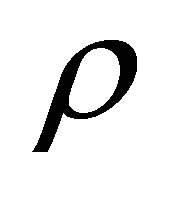 is the electrical resistivity distribution in 2-D circular domain
is the electrical resistivity distribution in 2-D circular domain ,
, 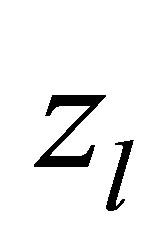 is the contact impedance on l-th electrode,
is the contact impedance on l-th electrode, 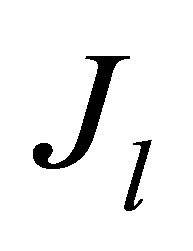 is the electric current density at l-th electrode respectively,
is the electric current density at l-th electrode respectively, 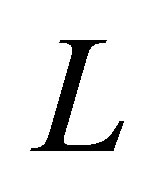 is the total electrode numbers.
is the total electrode numbers.
In this paper, we subdivided the 2-D circular solution domain into small cells by using Finite Element Method (FEM) (see Figure 2).
The EIT problem is an ill-posed inverse problem. Given the electrical resistivity distribution in the solution domain and the injected current at the body’s surface, the forward problem of the EIT is to solve the potential distribution in the solution space. The inverse problem is to reconstruct the resistivity distribution by the measuring electrical potential at the electrodes.
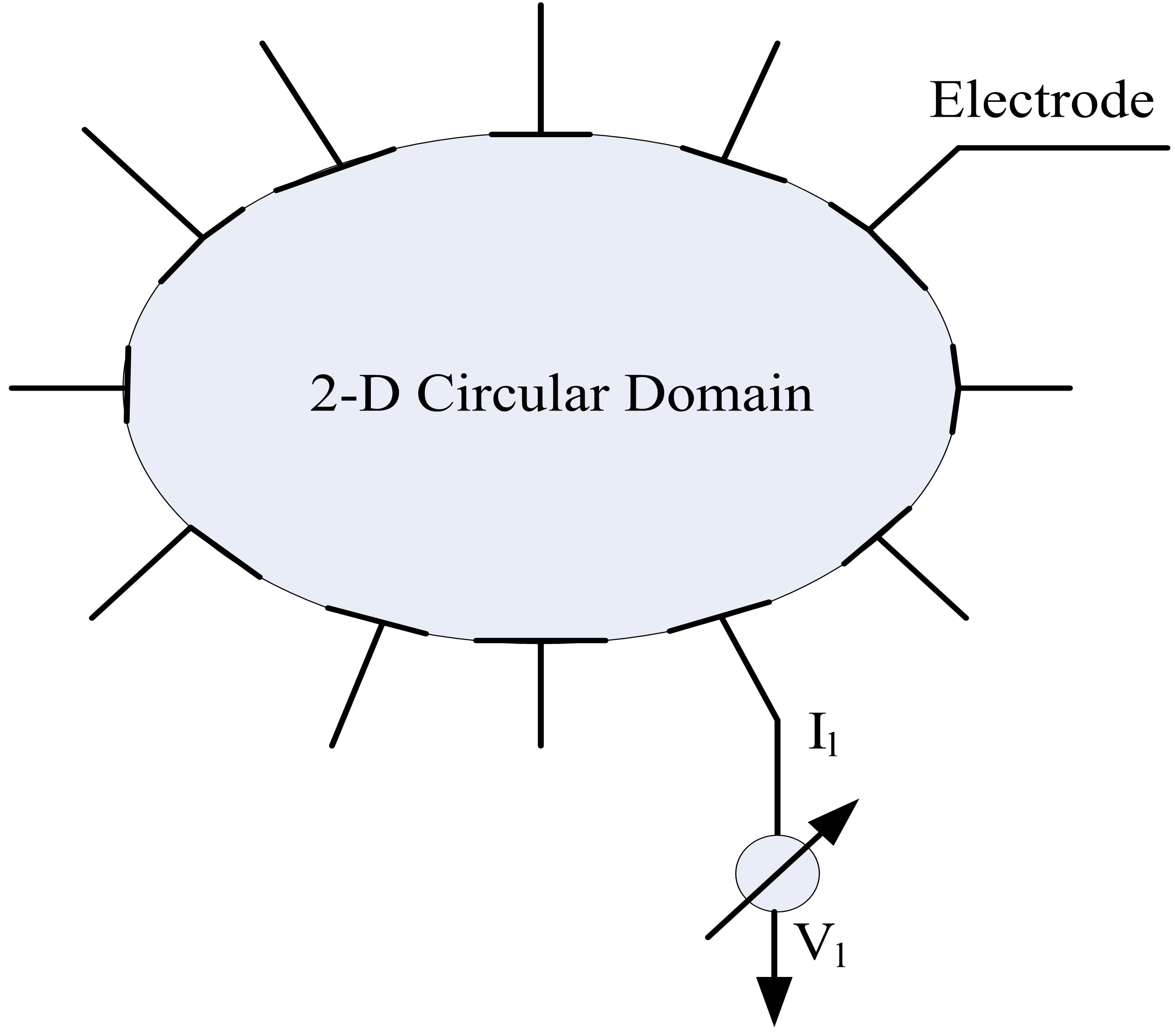
Figure 1. Principle of operation of EIT.

Figure 2. 2-D circular model.
For the all-electrode current model, the EIT problem can be written as [11]:
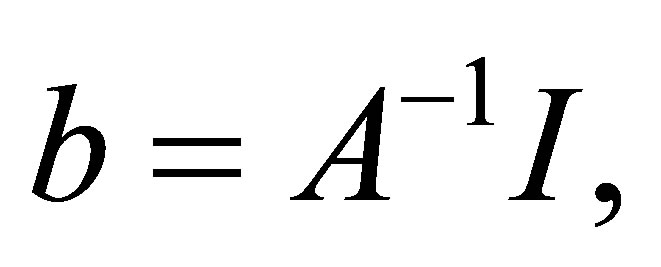 (5)
(5)
where, 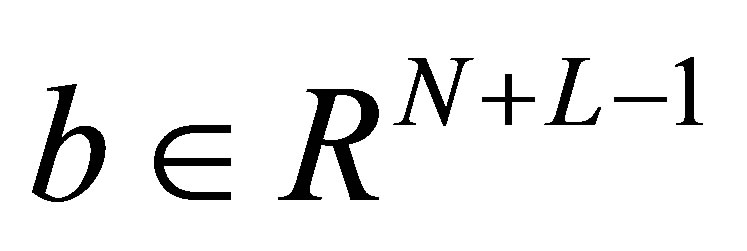 , the elements from 1 to
, the elements from 1 to 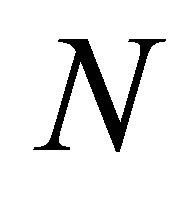 of the matrix
of the matrix  are the electrical potential of all FEM node in solution domain, and from
are the electrical potential of all FEM node in solution domain, and from 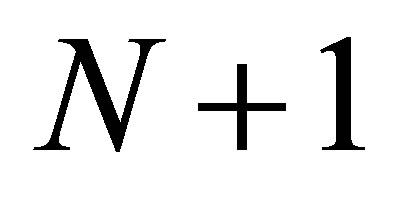 to
to 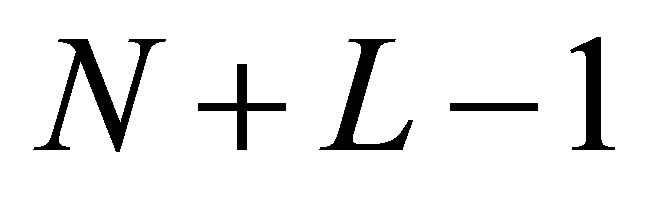 are the electrode potential.
are the electrode potential. 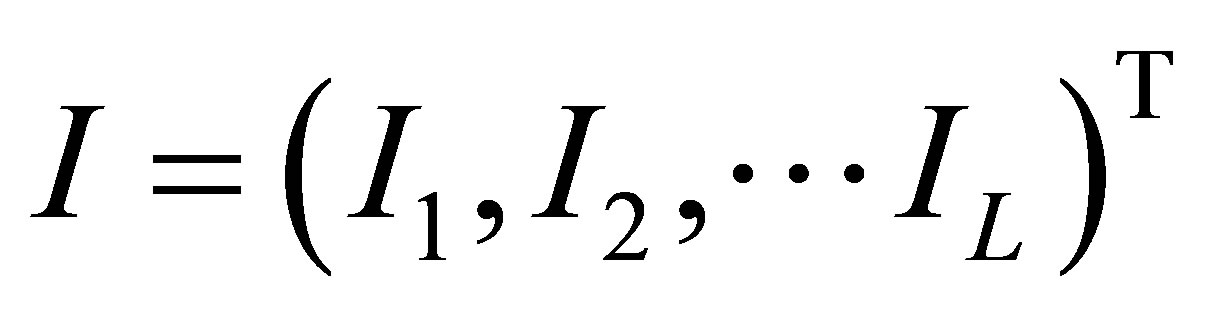 is the vector of the injecting electrical current. The matrix
is the vector of the injecting electrical current. The matrix  consists of the stiffness matrix of FEM and the coefficient matrix of the electrodes.
consists of the stiffness matrix of FEM and the coefficient matrix of the electrodes.
The iterative method is used to reconstruct the resistivity distribution. Given the initial value of the MPSOMNR algorithm at random, to update constantly the resistivity distribution by comparing the changes of the fitness value and the total error until the end condition is satisfied.
3. MPSO-MNR Algorithm
PSO has been shown to be effective in optimizing difficult multidimensional discontinuous problems in a variety of fields, it is not rigorous demand for the iterative initial value. MNR has the high computational efficiency when the starting trial solution is closed to the true value. In view of the advantages of the PSO and MNR algorithm, the MPSO-MNR algorithm is formed in EIT. The idea of the MPSO-MNR is to produce an initial value closed to the true value by MPSO, to acquire the resistivity distribution through MNR algorithm.
3.1. Modified Particle Swarm Optimization
PSO is a kind of stochastic, evolutionary and global optimization algorithm. In this algorithm, the solution of each optimization problem is a bird in search space, which is called particle. All particles have its fitness value determined by the optimization function, and each particle’s fly direction and distance are determined by its velocity. The particle swarm is updated by tracking the personal best (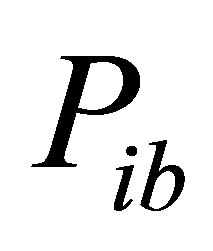 ) and global best (
) and global best (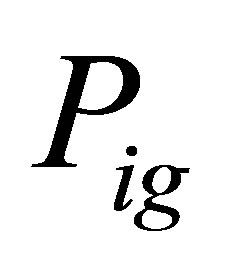 ) at each iteration [6,7,10].
) at each iteration [6,7,10].
In this paper, MPSO updates the population using the population mutation method, which is to update some particles using (6), and the other particles track the personal best and global best by using (7), (8),
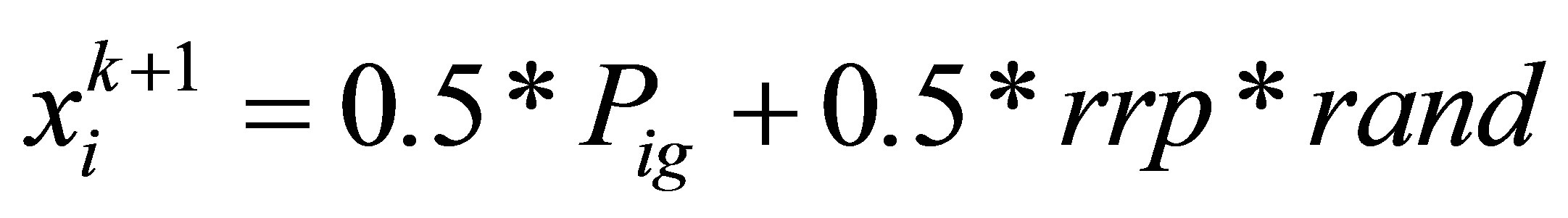 , (6)
, (6)
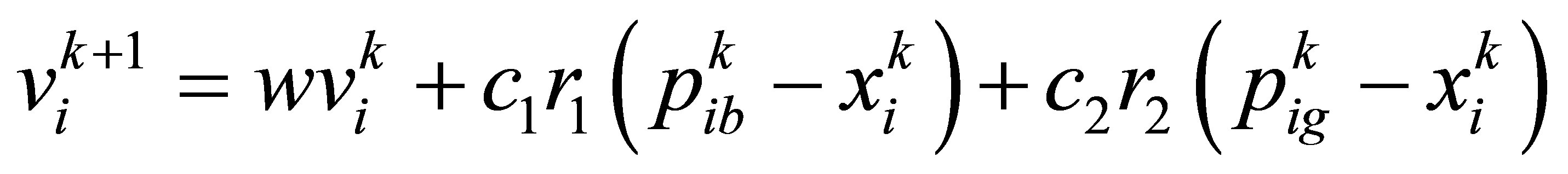 , (7)
, (7)
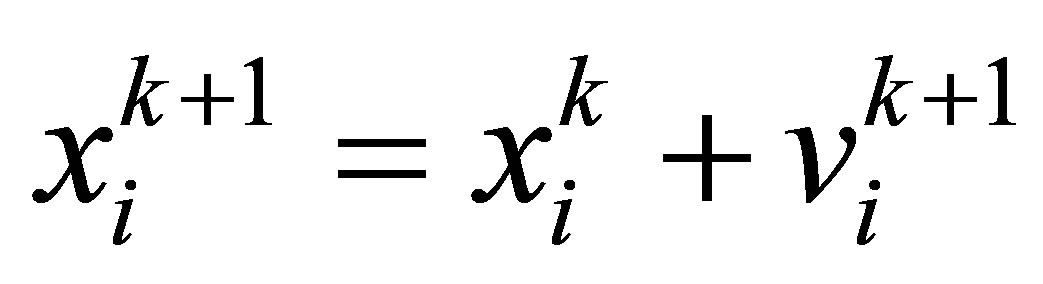 , (8)
, (8)
where 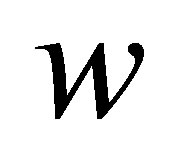 is dynamic inertia weight,
is dynamic inertia weight, 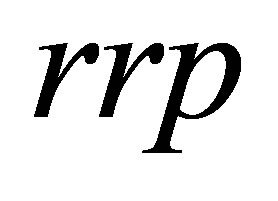 is the maximum empirical value of the electrical resistivity in solution domain,
is the maximum empirical value of the electrical resistivity in solution domain, 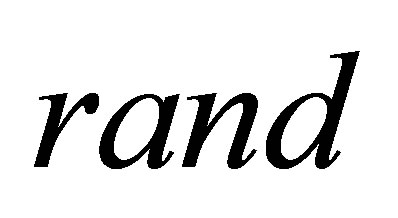 is the random number between 0 and 1.
is the random number between 0 and 1.
Definition: Fitness Value Function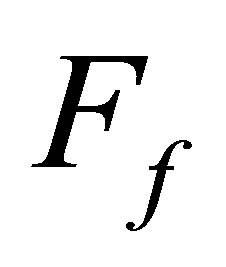 :
:
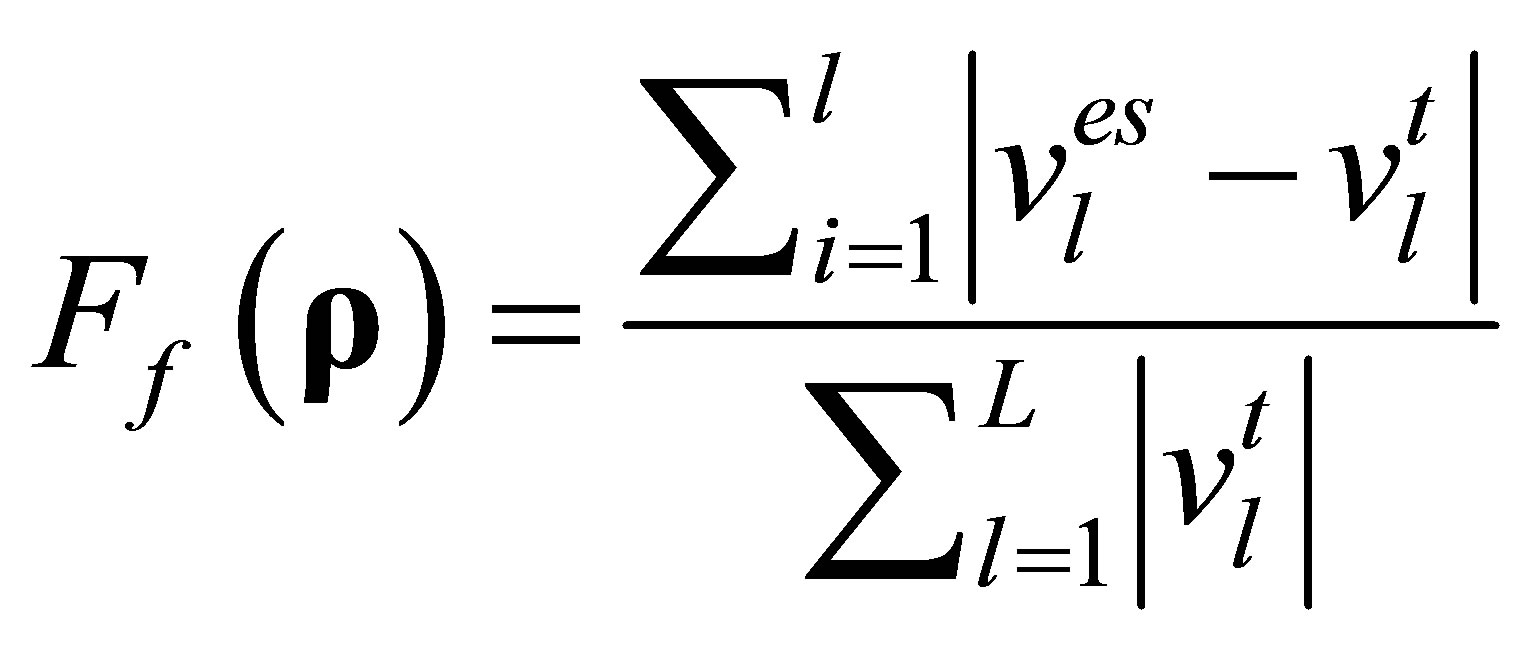 . (9)
. (9)
3.2. MNR Algorithm
Definition: Objective Function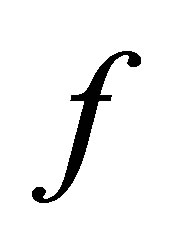 :
:
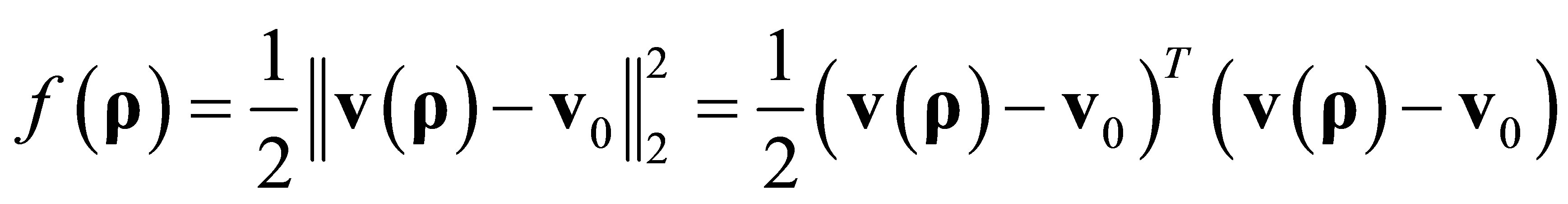 ,(10)
,(10)
where  is the vector of the electrical resistivity distribution,
is the vector of the electrical resistivity distribution, 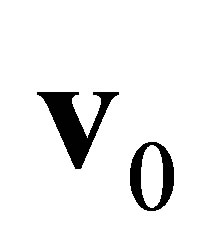 ,
, 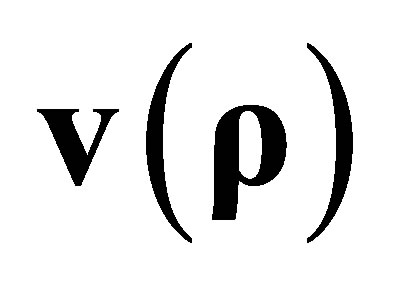 are the measuring and the calculation electrical potential value at the surface electrode, respectively. The
are the measuring and the calculation electrical potential value at the surface electrode, respectively. The 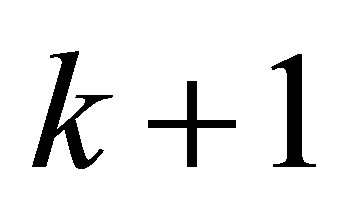 -th iteration of
-th iteration of  using MNR algorithm is
using MNR algorithm is
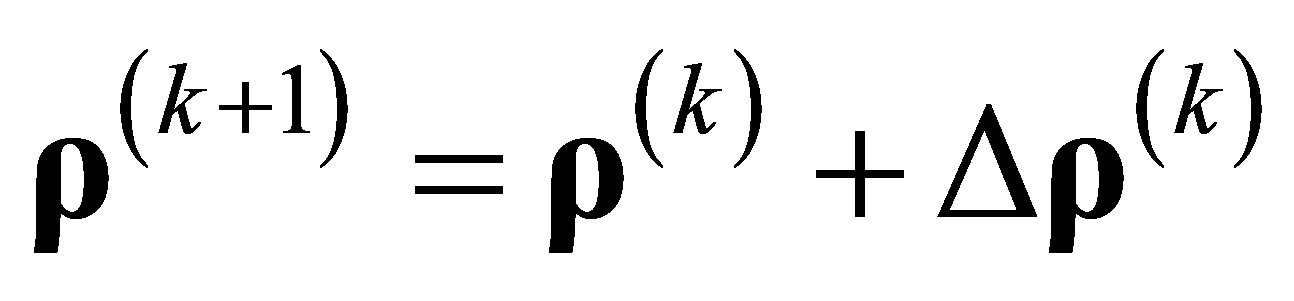 , (11)
, (11)
where
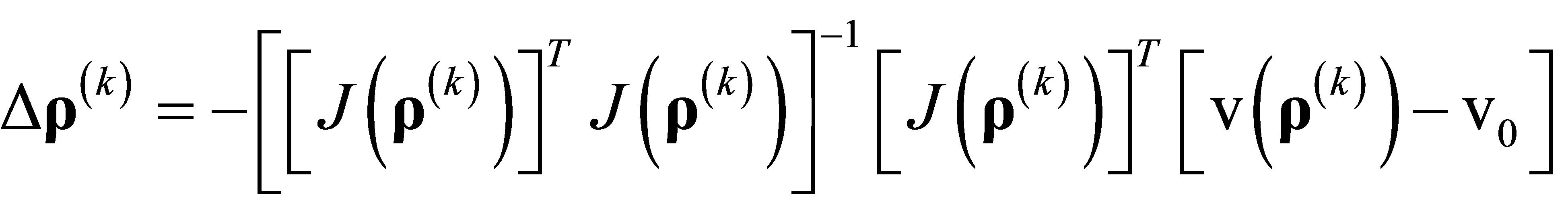 , (12)
, (12)
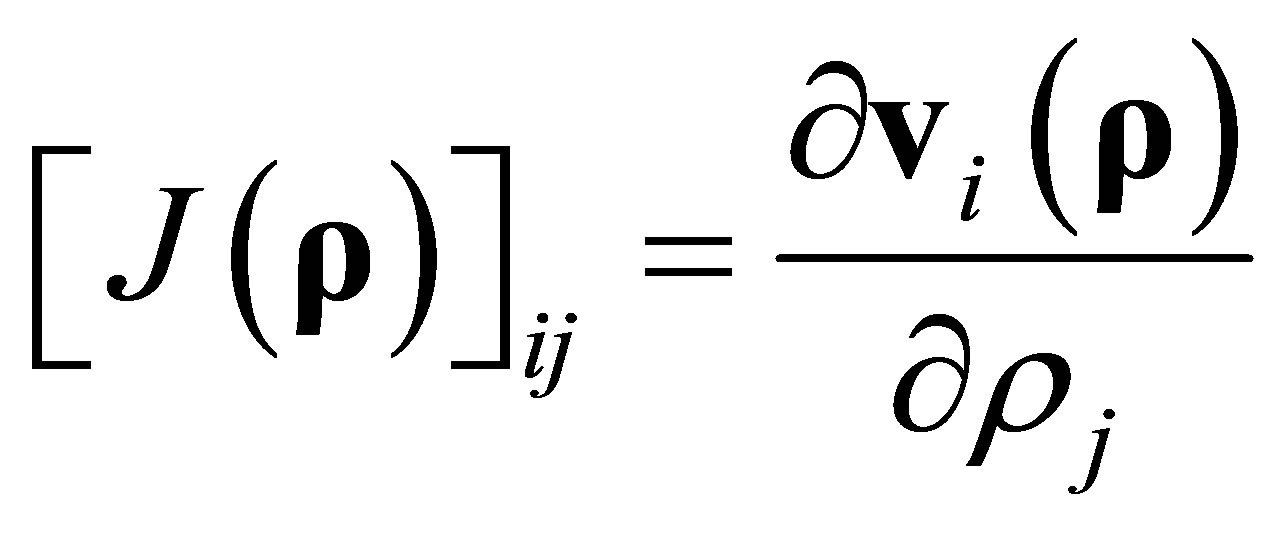 (13)
(13)
is the Jacobian matrix.
3.3. MPSO-MNR Algorithm Flow [9]
1) Set up the FEM model in the solution space.
2) Obtain the initial value of the MNR by the MPSO algorithm.
Step a). Initialization. Initialize the particle position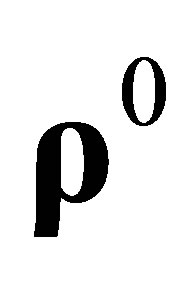 , velocity
, velocity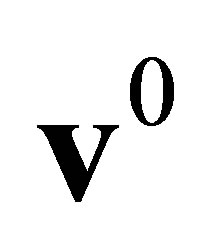 , Set the acceleration constant
, Set the acceleration constant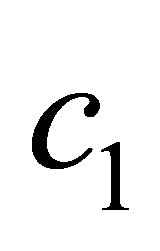 ,
, 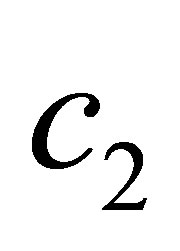 and inertia constant
and inertia constant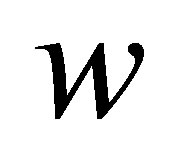 .
.
Step b). Calculate and evaluate the particle’s fitness value, compare and obtain the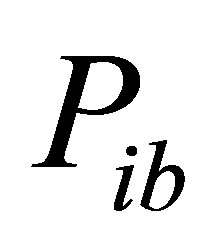 ,
,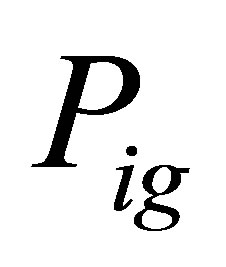 .
.
Step c). Calculate the particle’s velocity, update the swarm.
Step d). Repeat.
3) Reconstruct by the MNR algorithm.
Step a). Using the numerical result of the MPSO algorithm as the initial value , to calculate the objective function value
, to calculate the objective function value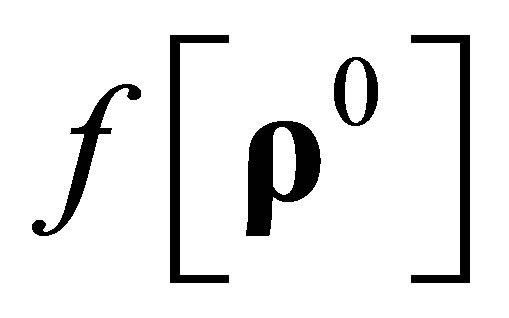 .
.
Step b). If the end condition is met, end iteration, else go to step c).
Step c). Calculate objective function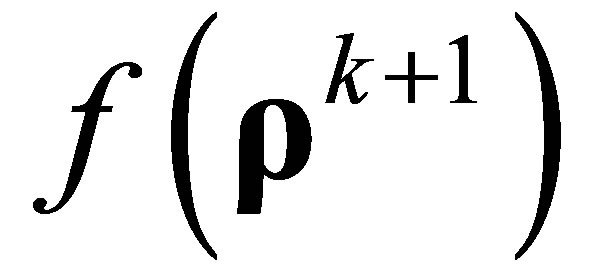 .
.
Step d). Calculate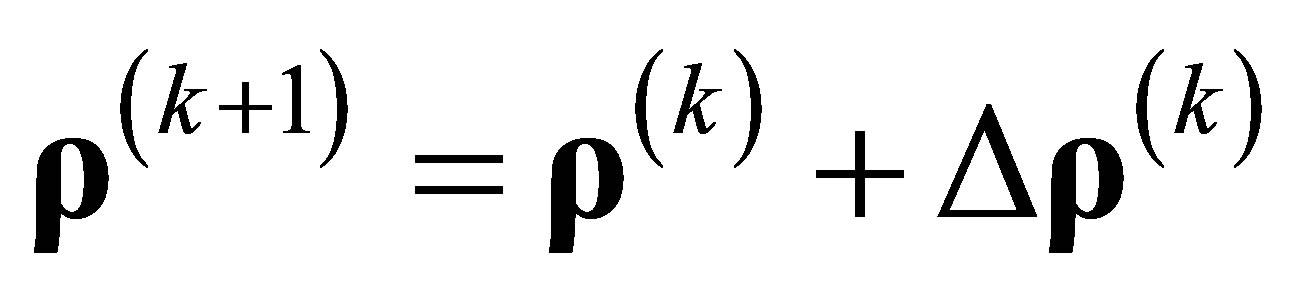 ,
, 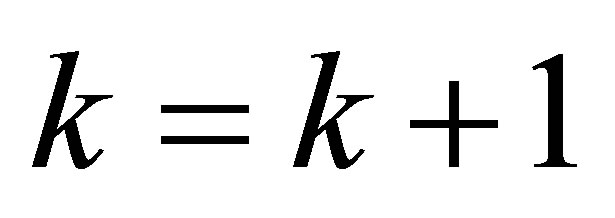 , go to step b).
, go to step b).
4. Numerical Simulation
Definition: Total Error (TE)
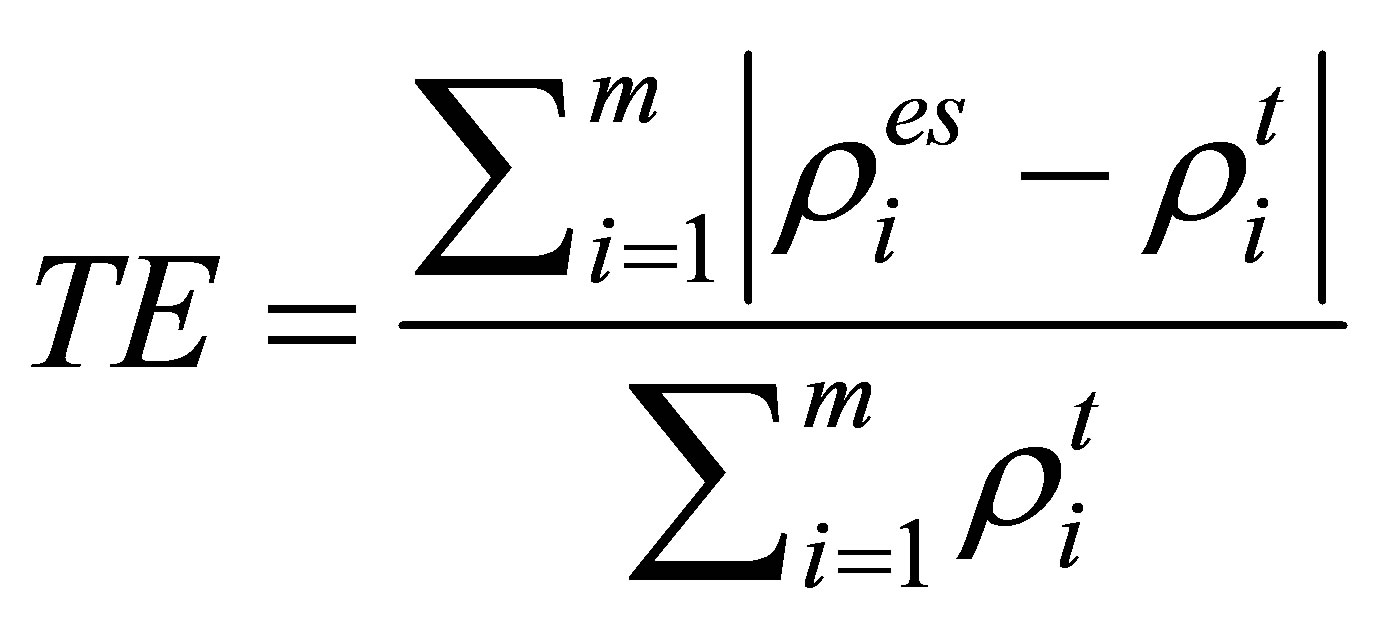 (14)
(14)
where 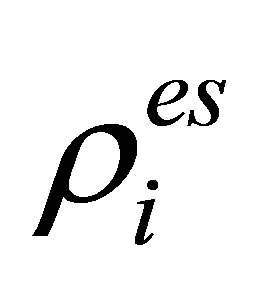 and
and 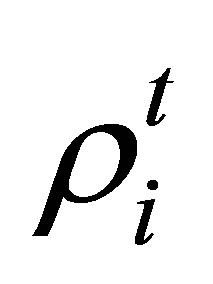 are the reconstruction value and the true value of the resistivity in the solution domain, respectively.
are the reconstruction value and the true value of the resistivity in the solution domain, respectively. 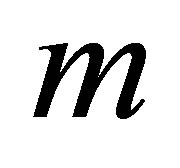 is the element numbers of the solution domain.
is the element numbers of the solution domain.
Definition: Signal-to-Noise Ratio (SNR)
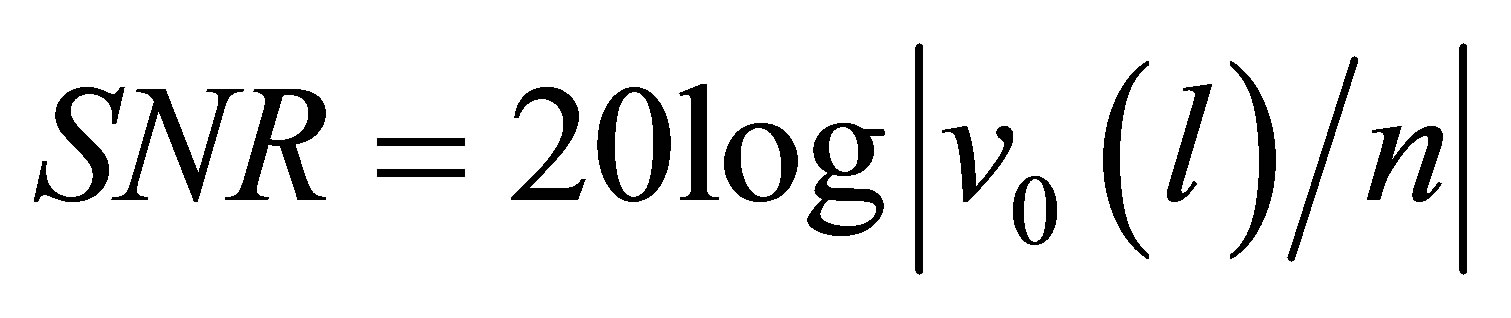 , (15)
, (15)
where 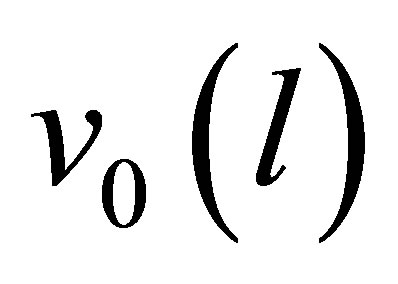 is the measure potential value at the
is the measure potential value at the 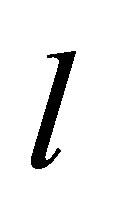 -th,
-th, 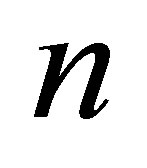 is the sampling noise amplitude.
is the sampling noise amplitude.
4.1. Single Target Simulation
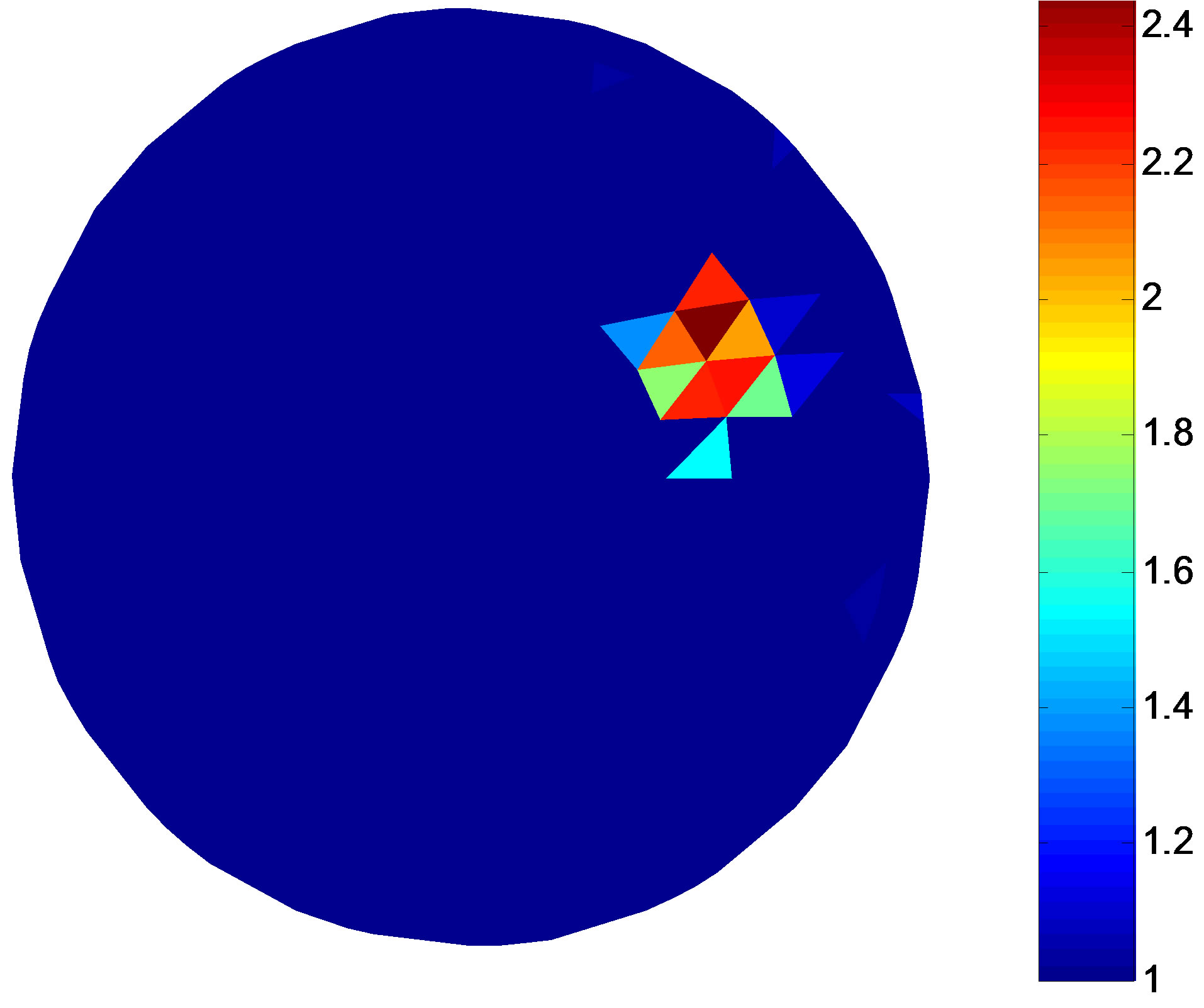
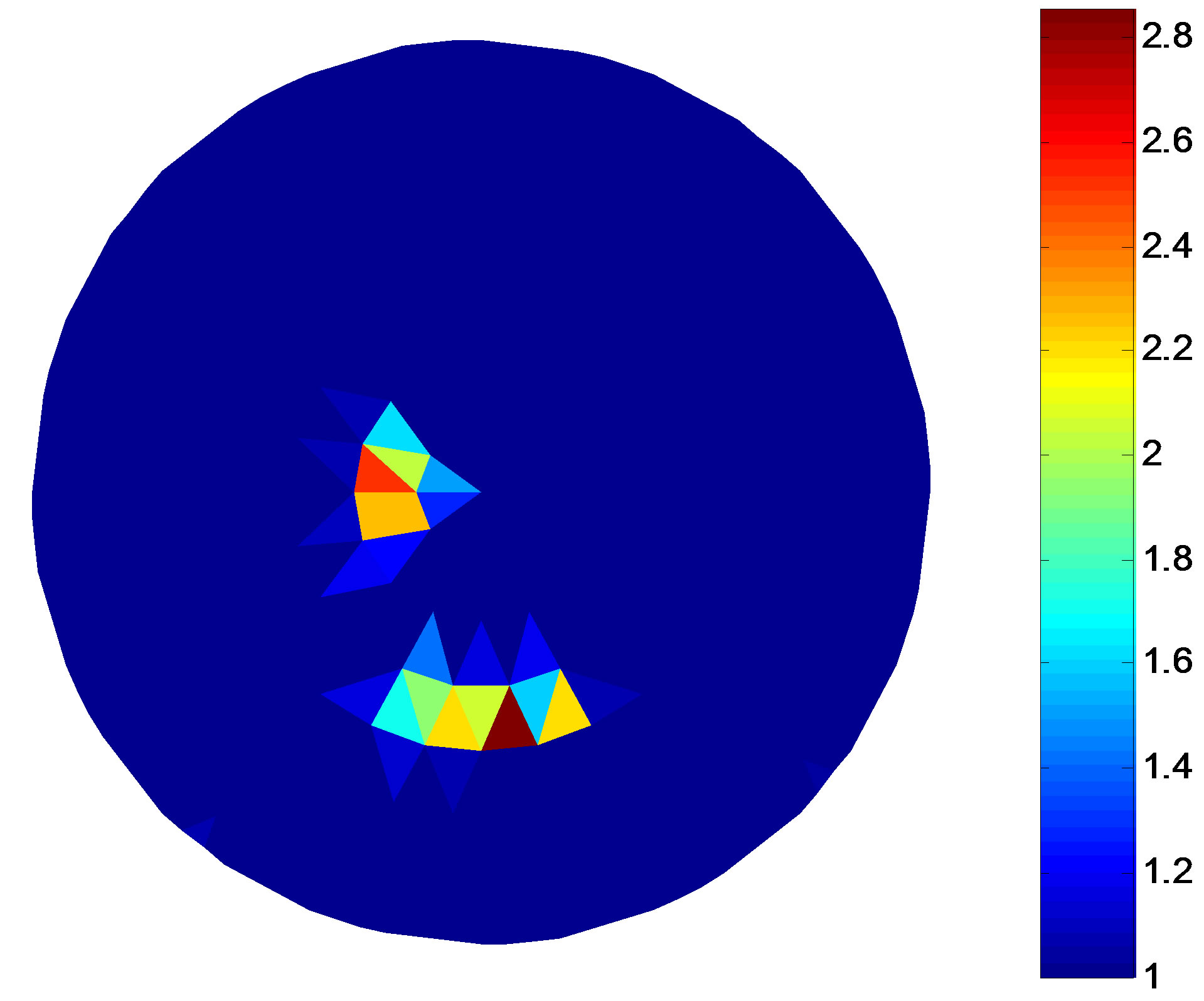
A simulation target is set in the 2-D circular domain (see Figures 3(a) and 4(a)), the background resistivity is 1 Ω·m, the target is 2.3 Ω·m. The iterative initial value of the MPSO algorithm is set as the random value between 1 and the empiric value. According to the trend of the fitness value and the total error with the number of iterations, the economic iterations of the MPSO should be about 10 times, MNR algorithm about 20 times [9]. In order to compare the reconstruction results in different configurations and noise levels, the 50-th iteration results of the MPSO is serve as the iterative initial value of the MNR algorithm, the end condition of the MPSO-MNR algorithm is at 60-th times of the MNR iteration in this paper.
The colour scale in Figures 3 and 4 represents the level of the resistivity. Figures 3 and 4 are the simulation targets and the reconstruction results in different noise levels, respectively. The target in Figure 4(a) closes to the centre of the solution domain compared with Figure 3(a). Comparing Figures 3 and 4, the numerical results show that the border of the reconstruction object is getting vague and the background become non-uniform with the target moving to the centre of the circular domain. Noise affects the imaging quality. With the increase of the noise, that is the decreasing SNR, the border of the
 (a)
(a)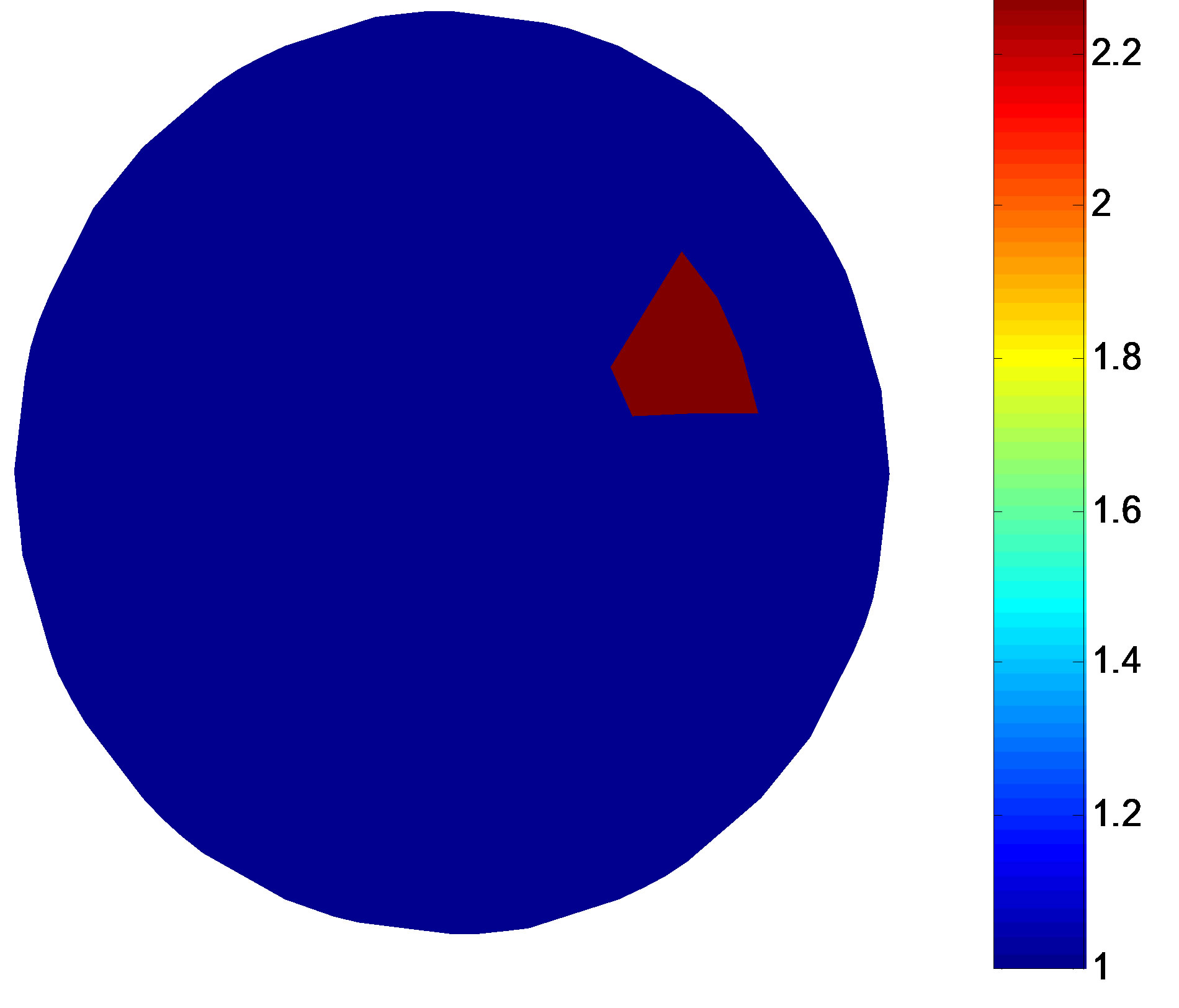 (b)
(b)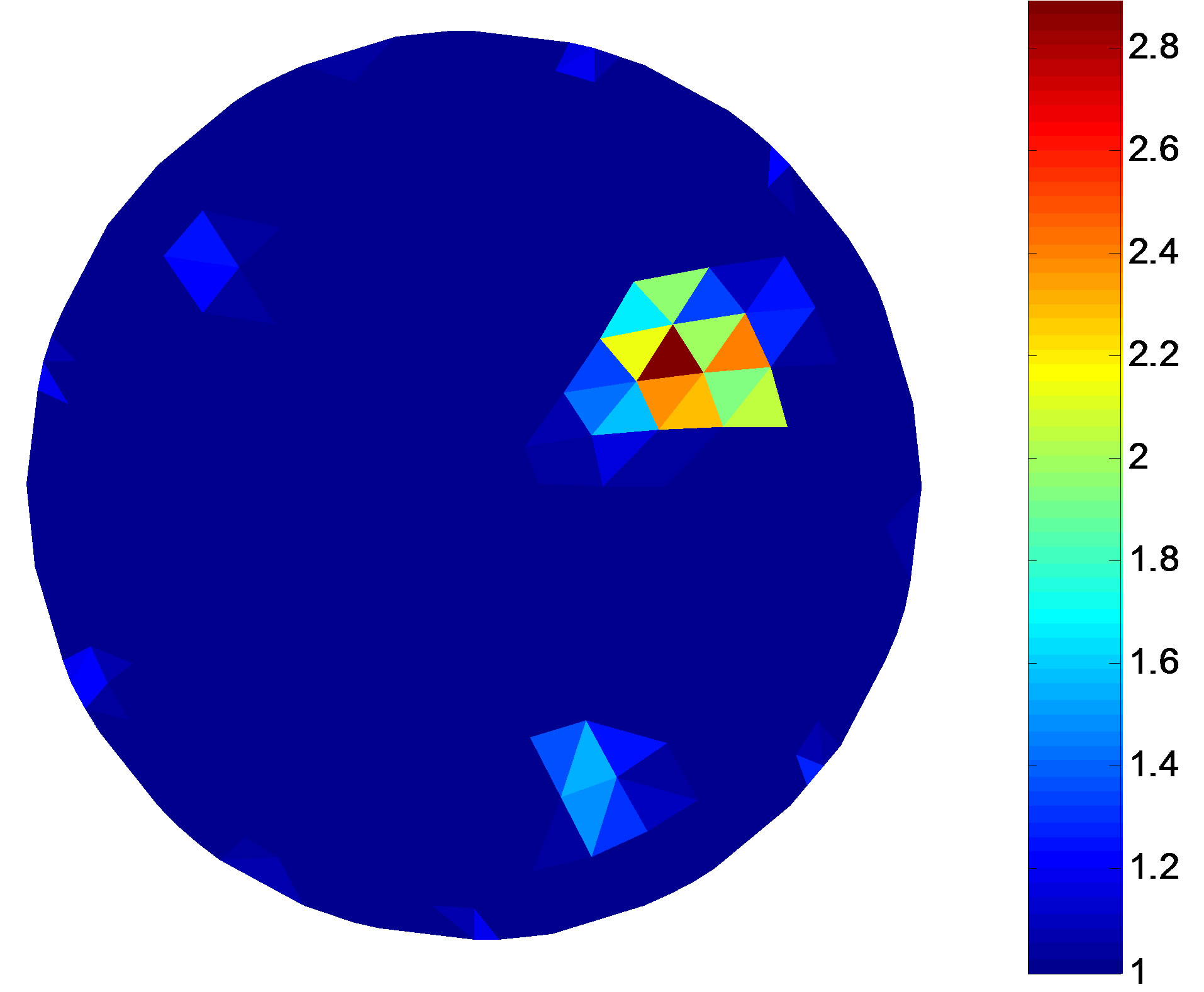 (c)
(c) (d)
(d)
Figure 3. Simulation model and the reconstruction result of the single target. (a) Simulation target; (b) Reconstruction result (non-noise); (c) Reconstruction result (SNR = 40 dB); (d) Reconstruction result (SNR = 30 dB).
 (a)
(a)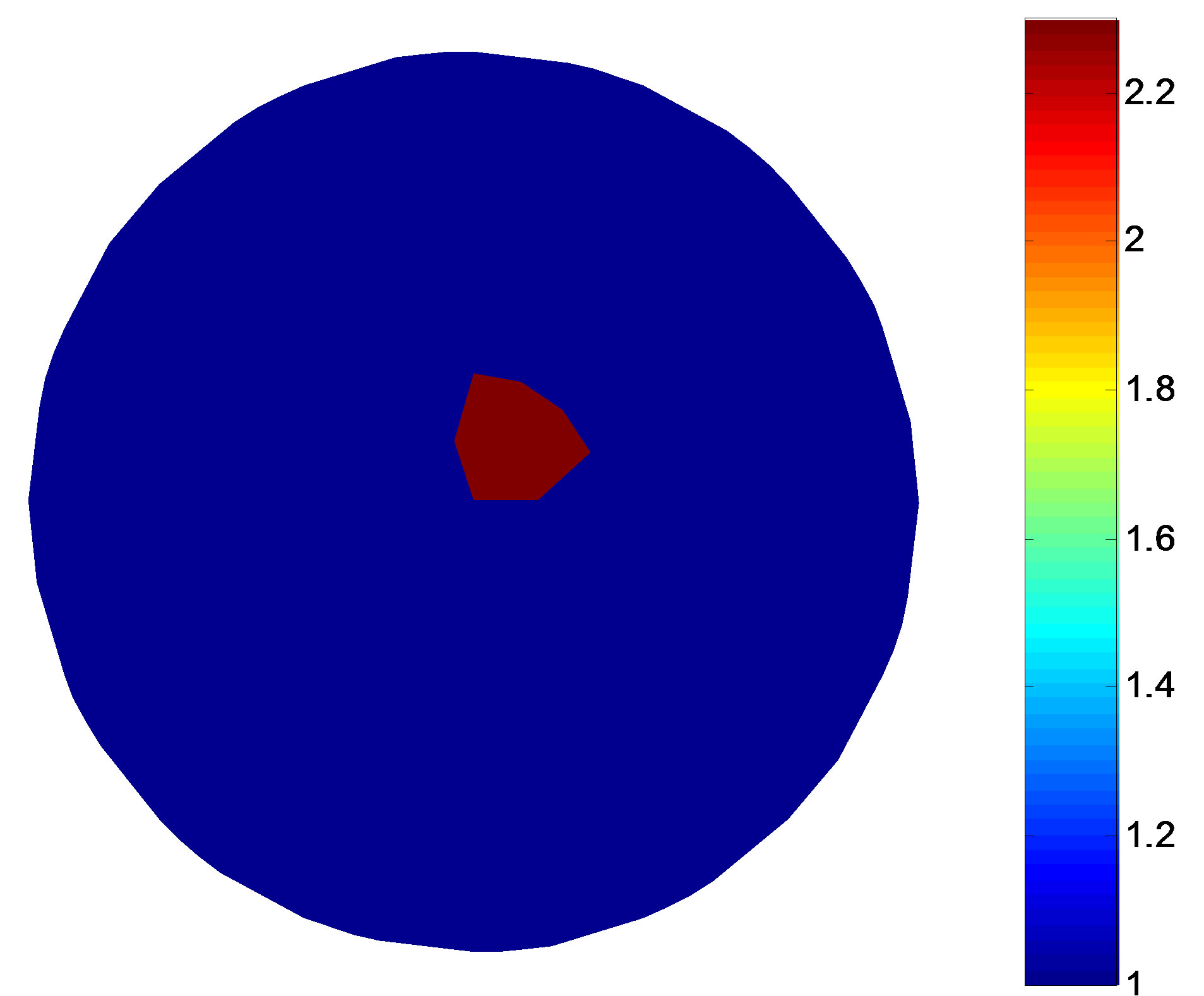 (b)
(b)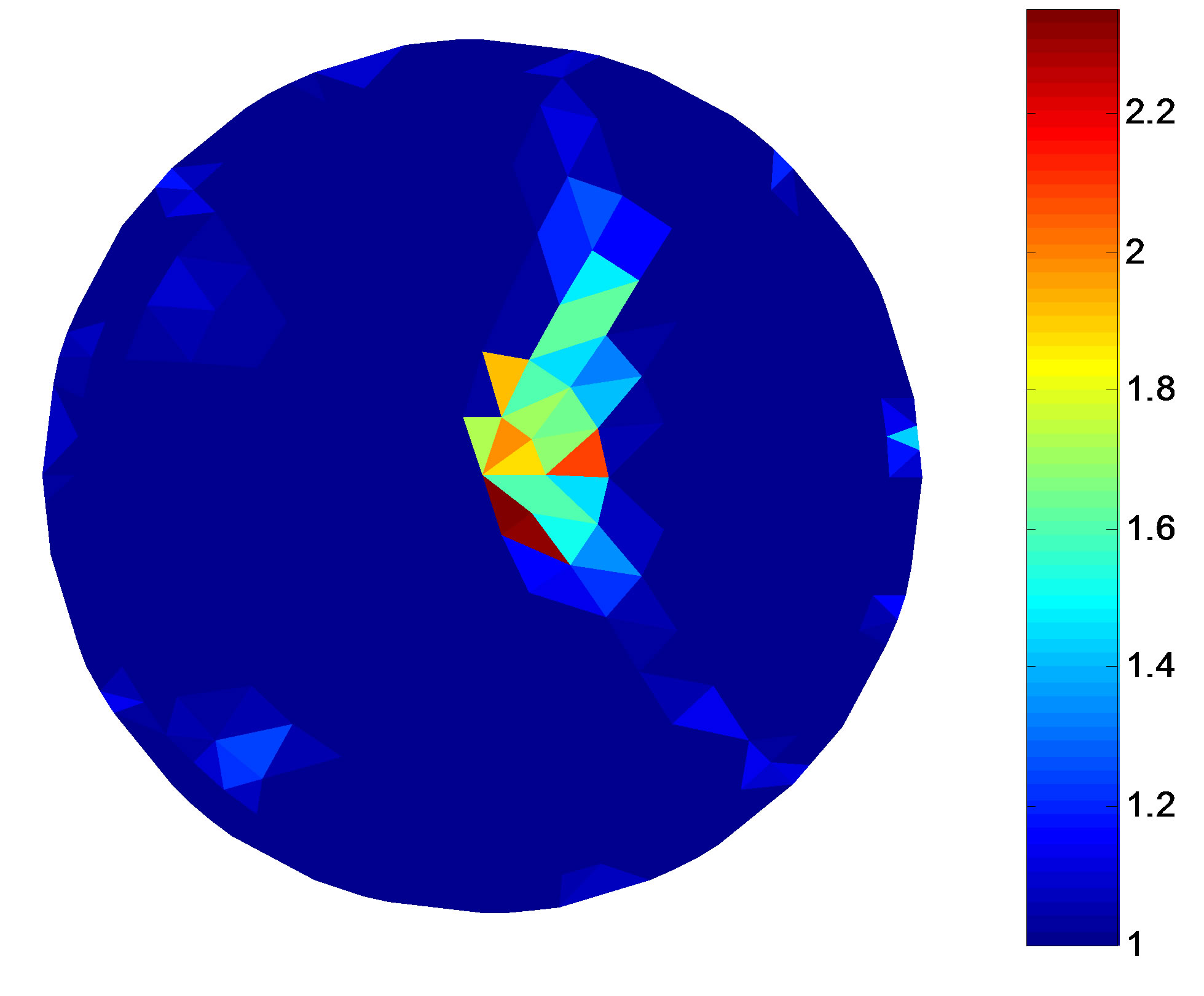 (c)
(c)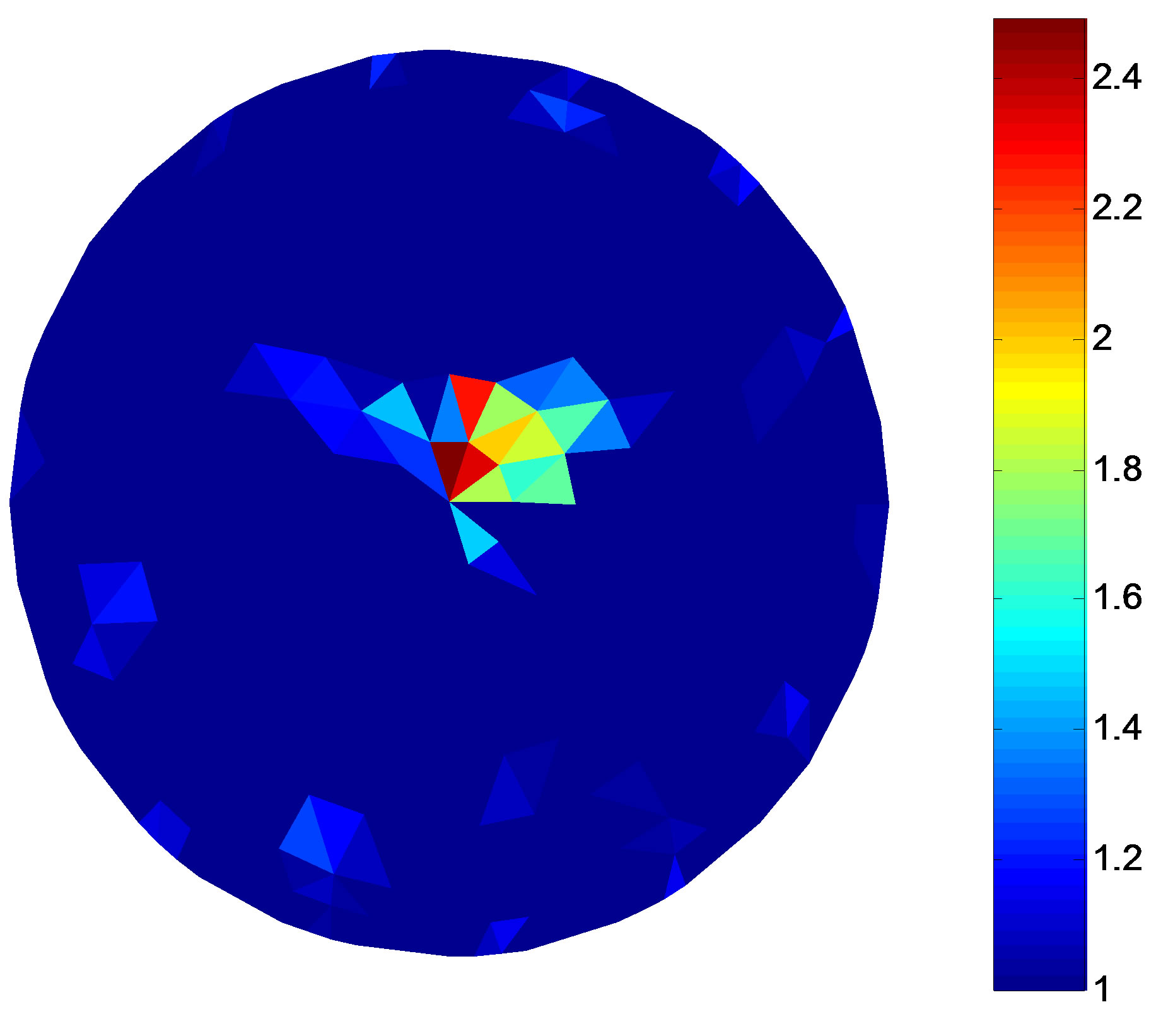 (d)
(d)
Figure 4. Simulation model and the reconstruction result of the single target. (a) Simulation target; (b) Reconstruction result (non-noise); (c) Reconstruction result (SNR = 40 dB); (d) Reconstruction result (SNR = 30 dB).
reconstruction object become vague.
The reconstruction quality of the EIT is evaluated by the fitness value and the total error. Table 1 gives the fitness value and the total error of the single target in different position and under different noise levels, which the number of the MPSO iterations are at 50-th times and MNR at 60-th times. Comparing the fitness value and the
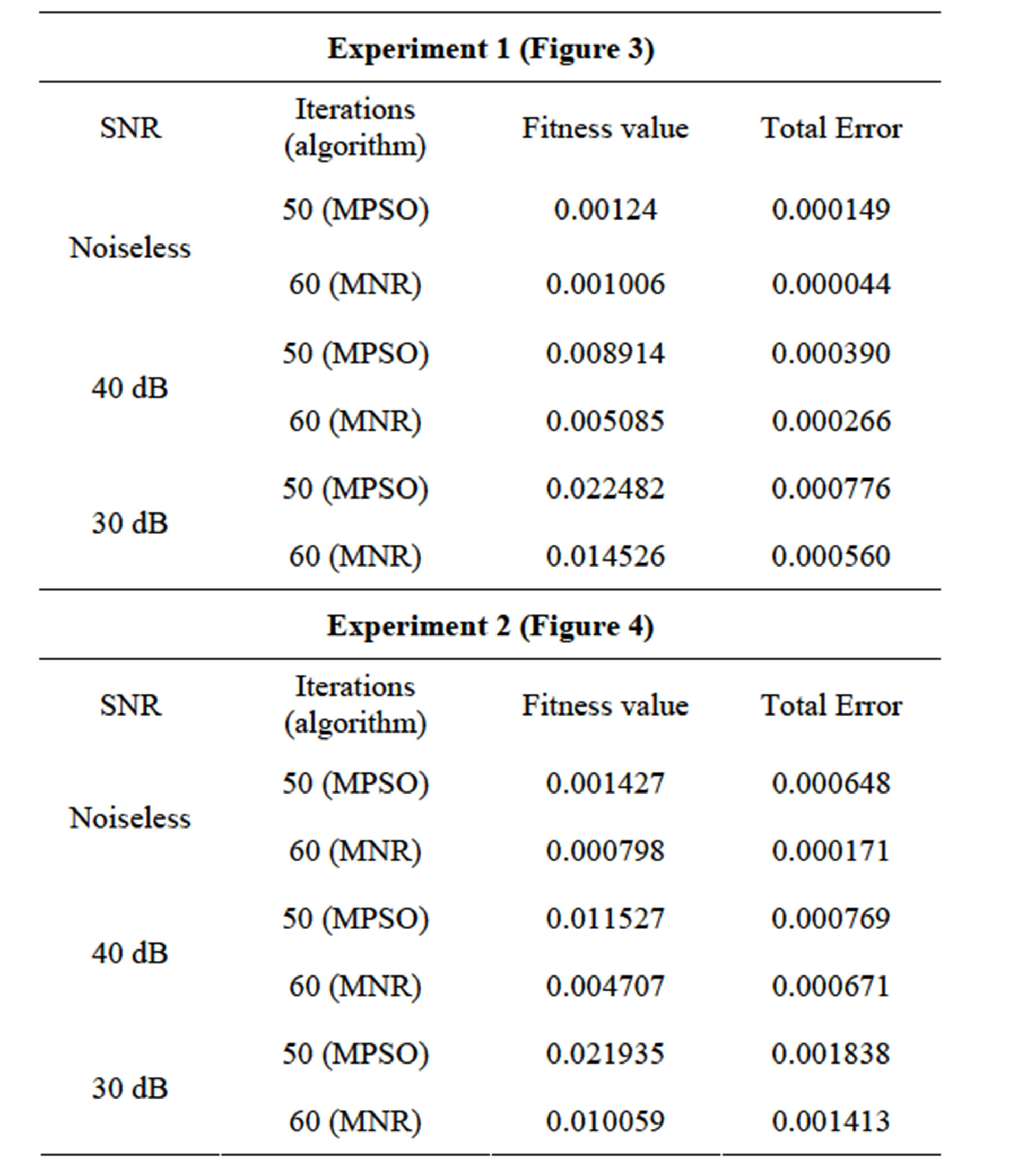
Table 1. Fitness value and the total error of the single target.
total error in different conditions, the results show that the fitness value and the total error increase gradually at same iterations with decreasing of the SNR and the target close to the centre of the solution domain, which means the lower imaging quality. This result is consistent with the results of the Figures 3 and 4.
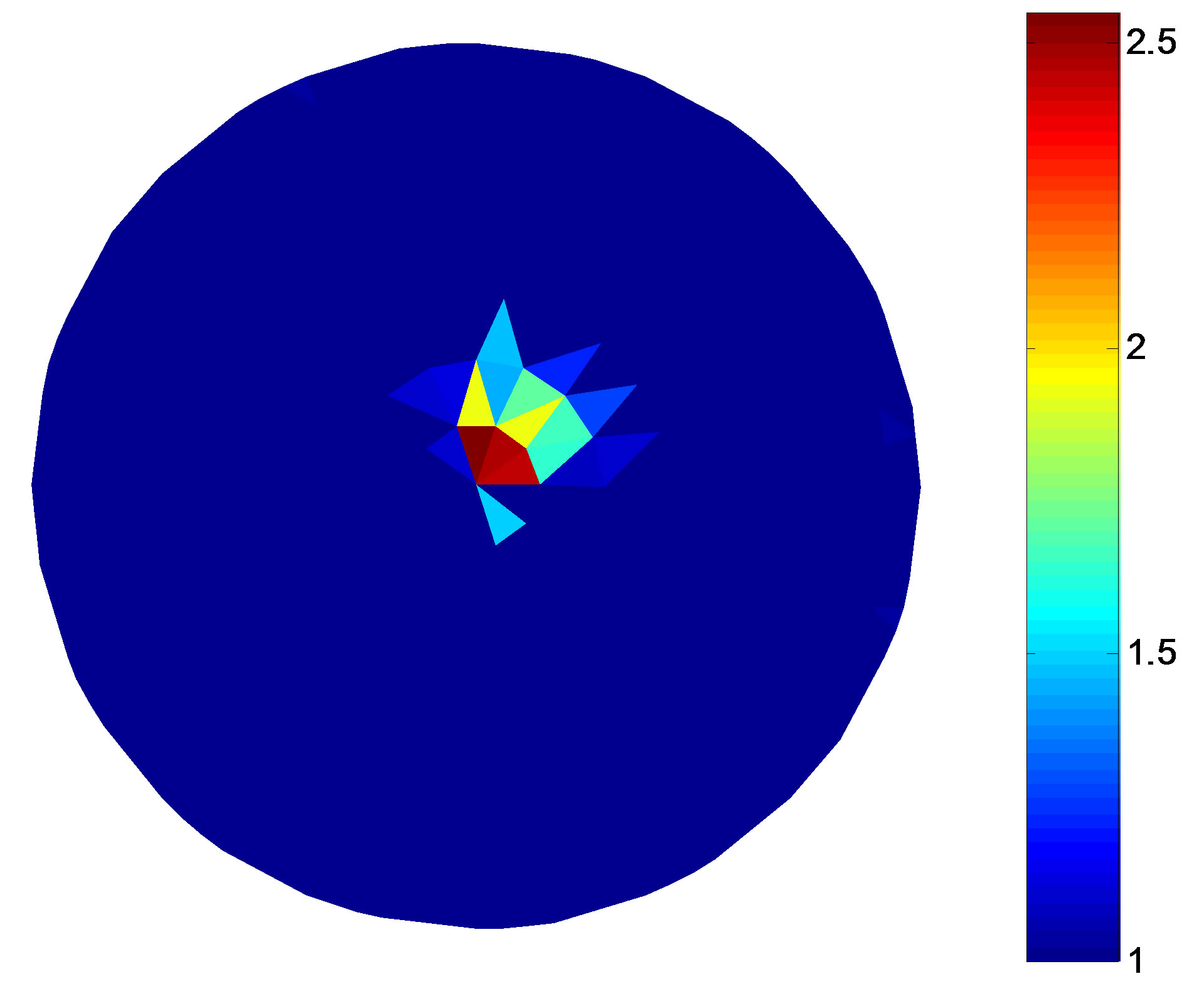
4.2. Two Targets Simulation
The two targets simulation is presented in this section. In the 2-D circular domain, the background resistivity is 1 Ω·m, and the target is 2.3 Ω·m. The setting of the iterative initial value and the end condition is same as the setting of the single target simulation.
Figure 5 shows the simulation targets and the reconstruction results under different noise levels. The fitness value and the total error are presented in Table 2. The results show that the reconstruction targets border become vague the fitness value and the total error increase gradually with the increase of noise.
5. Conclusions
Algorithm research is an important issue in EIT technique. The MPSO-MNR algorithm is formed by the MPSO algorithm and the MNR algorithm. It draws the advantages of loosing the initial value demand and the feature of the global convergence in MPSO algorithm,
 (a)
(a)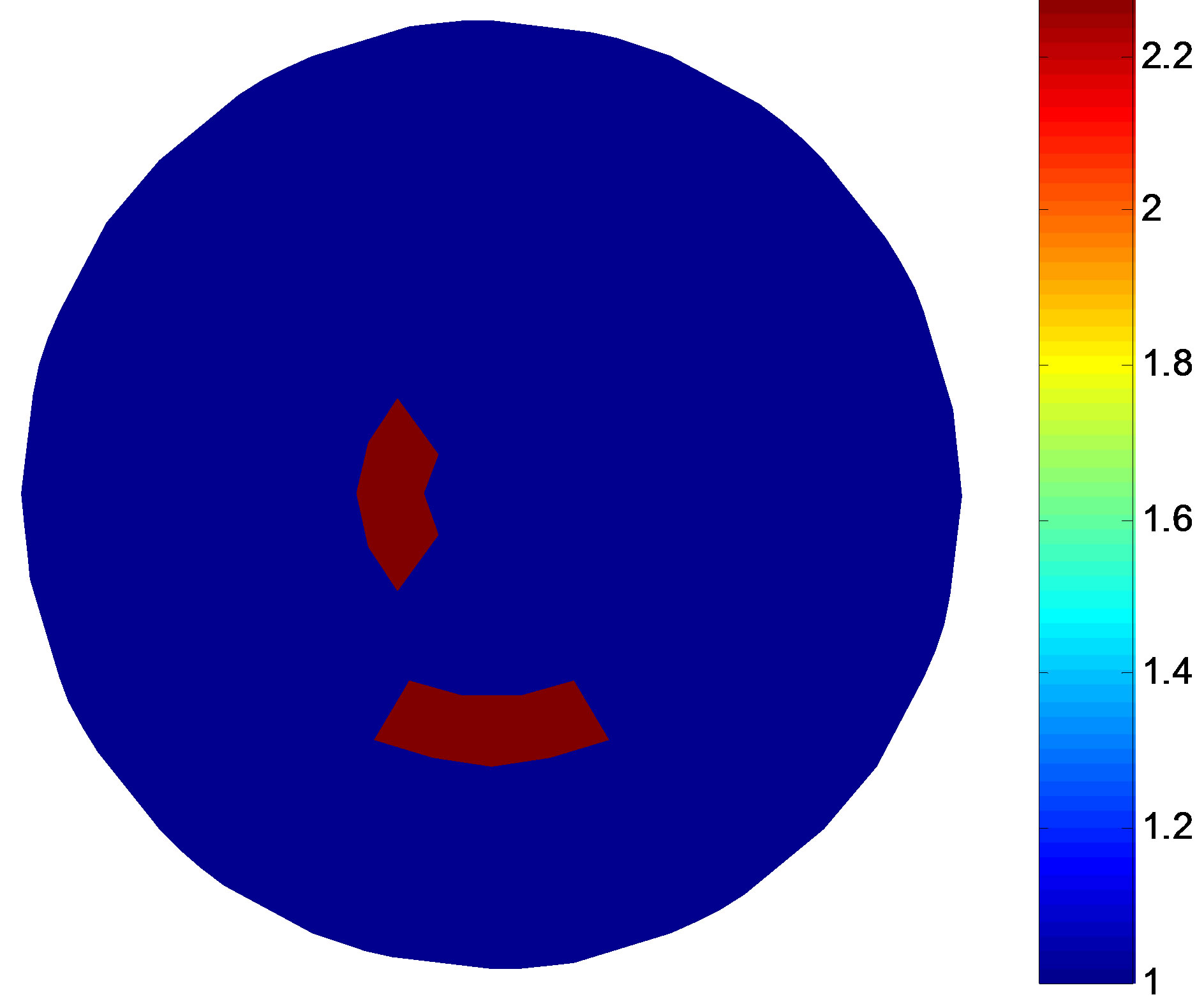 (b)
(b)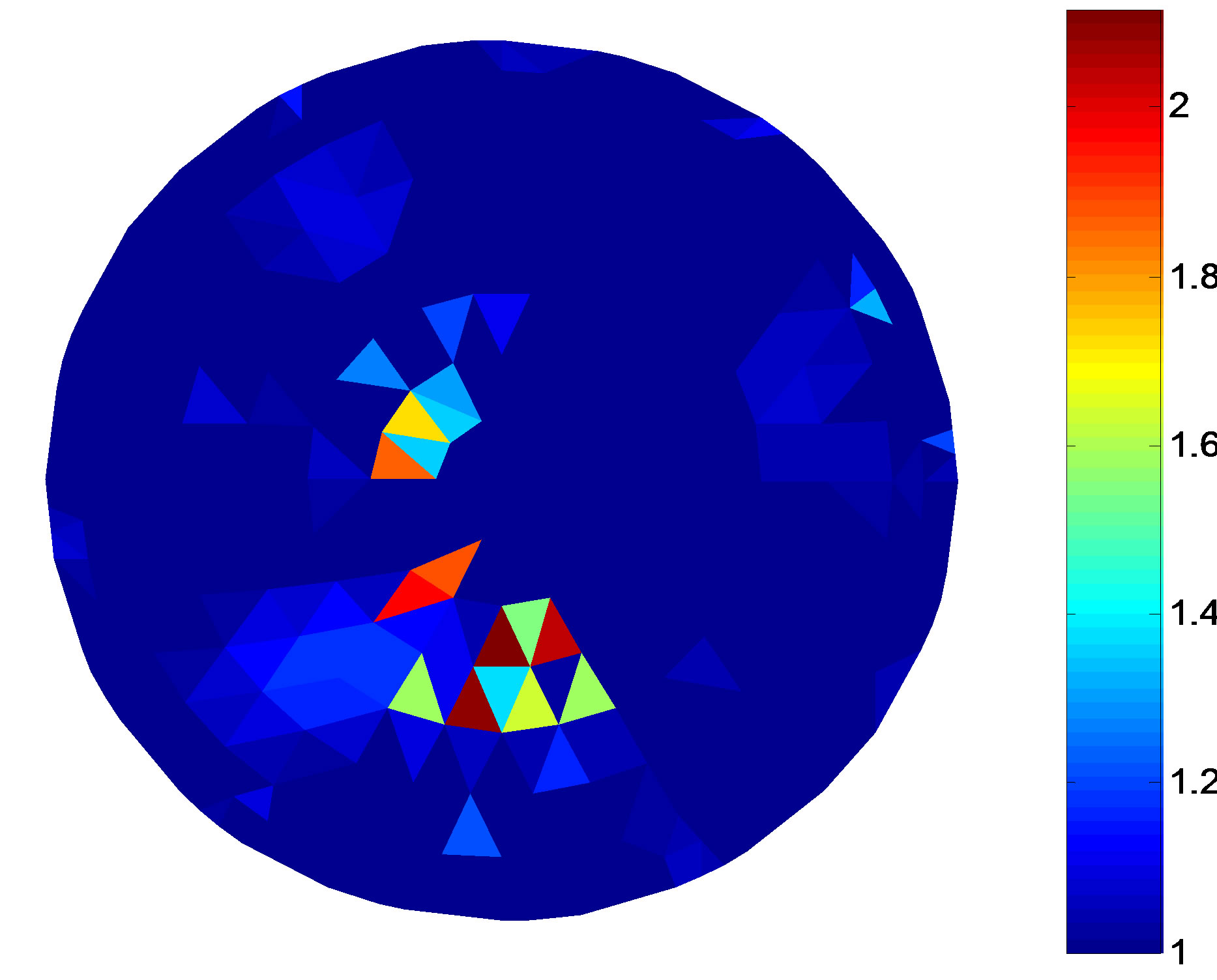 (c)
(c)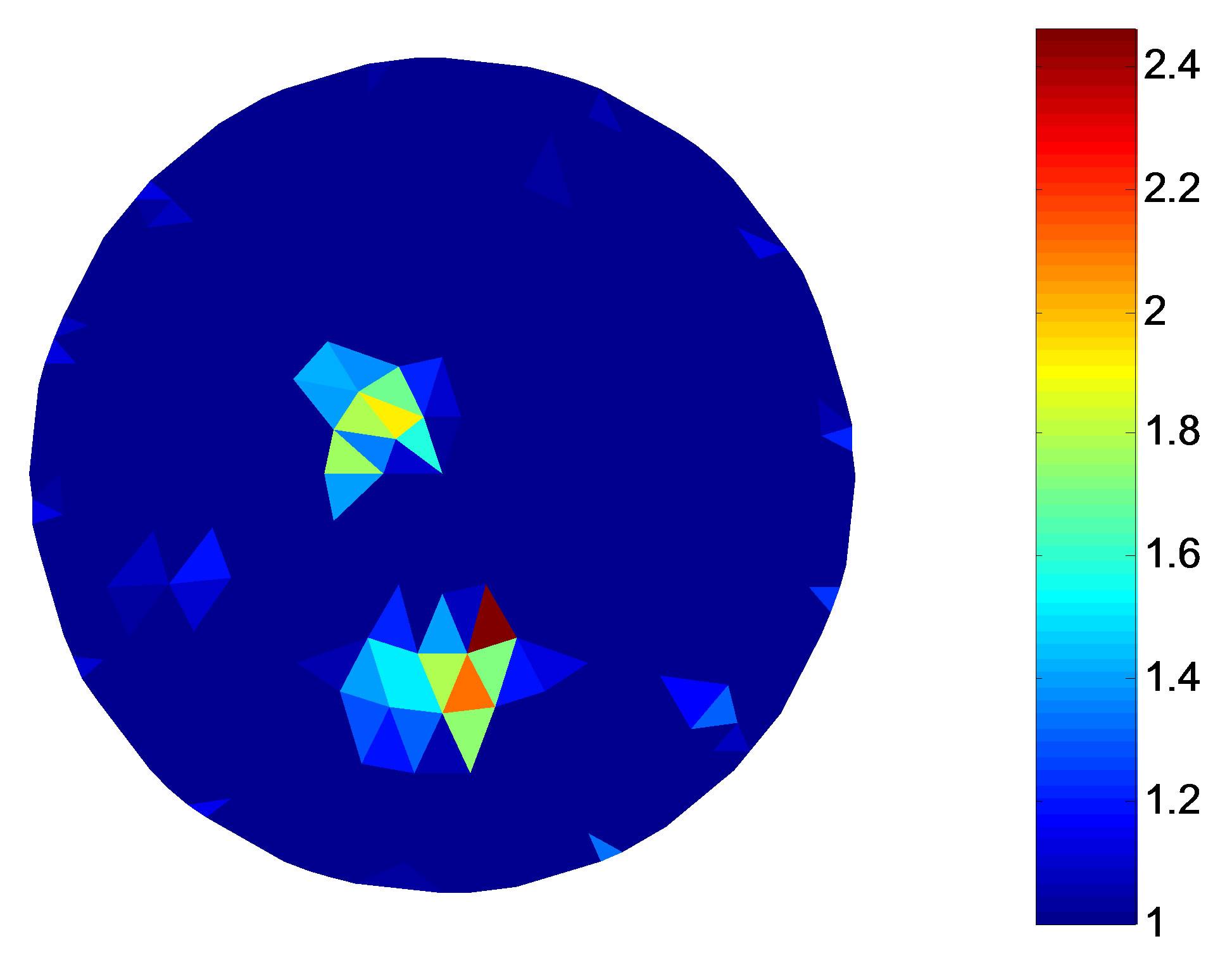 (d)
(d)
Figure 5. Simulation experiment model and the reconstruction result of the two targets. (a) Simulation target; (b) Reconstruction result (non-noise); (c) Reconstruction result (SNR = 40 dB); (d) Reconstruction result (SNR = 30 dB).
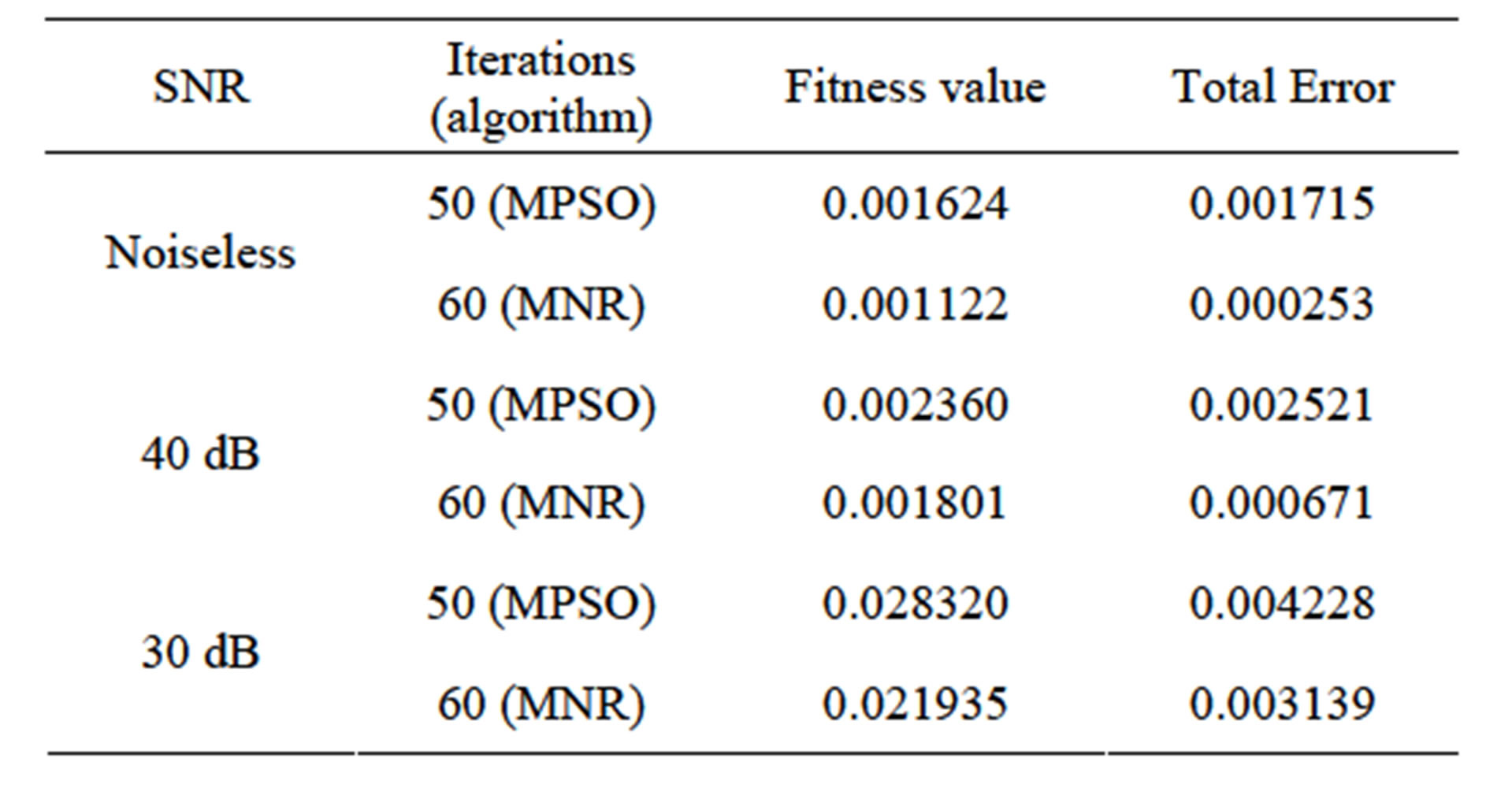
Table 2. Fitness value and the total error of the two targets.
avoids the demand of the initial value close to the true value and uses the advantages of the fast convergence speed of MNR algorithm.
The numerical results show that the MPSO-MNR algorithm can reflect the resistivity distribution in the solution space within the certain iterations. With the target moving to the centre of 2-D solution domain and the increasing of the noise, the border of the reconstruction objects becomes vague, and the fitness value and the total error increase gradually. This suggests that the noise and the relative position of target influence the image quality.
Model degeneracy is a general difficulty in optimizing problems. In this paper, the resistivity distribution of the certain configuration can be reconstructed by MPSOMNR algorithm and the results show changes in performance under different noise levels. Therefore, the anti-noise algorithm will be the research direction in the practical application of the EIT. In addition, the effect of other configurations on MPSO-MNR will be the research works in EIT as well.
6. Acknowledgements
The authors would like to thank the reviewers whose thoughtful comments added to the efficacy of this paper. This work was supported by foundation of education department of Shaanxi provincial government (No. 2010JK892) and national college’s student innovative project (No. 201210722024).
REFERENCES
- H. Dehghani and M. Soleimani, “Numerical Modeling Errors in Electrical Impedance Tomography,” Physiological Measurement, Vol. 28, No. 7, 2007, pp. S45-S55. http://dx.doi.org/10.1088/0967-3334/28/7/S04
- G.-Z. Xu, Y. Li, et al, “Electrical Impedance Tomography in Biomedical Engineering,” China Machine Press, Beijing, 2010.
- W. He, C.-Y. Luo, Z. Xu, et al., “Principle of the Electrical Impedance Tomography,” Science Press, Beijing, 2009.
- Y. Li, G. Z. Xu, L. Y. Rao, et al., “MNR Method with Self-Determined Regularization Parameters for Solving Inverse Resistivity Problem,” Proceedings of 27th Annual International Conference of the IEEE Engineering in Medicine and Biology, Vol. 3, 2005, pp. 2653-2655.
- H. Zhang, Y.-J. Zhou and X.-D. Zhang, “Algorithm Study of 2-D Electrical Impedance Tomography,” Journal of Xianyang Normal University, Vol. 27, No. 2, 2012, pp. 17- 19.
- H. Zhang, X.-D. Zhang, et al., “Electromagnetic Imaging of the 2-D Media Based on Particle Swarm Algorithm,” 2010 Sixth International Conference on Natural Computation (ICNC), 10-12 August 2010, pp. 262-264.
- H. Zhang, H. B. Wang, Y. J. Zhou and X. D. Zhang, “Research of Electrical Impedance Tomography Based on the Modified Particle Swarm Optimization,” 2012 Eighth International Conference on Natural Computation (ICNC), 29-31 May 2012, pp. 1127-1129.
- R. Olmi, M. Bini and S. Priori, “A Genetic Algorithm Approach to Image Reconstruction in Electrical Impedance Tomography,” IEEE Transactions on Evolutionary Computation, Vol. 4, No. 1, 2000, pp. 83-88. http://dx.doi.org/10.1109/4235.843497
- H. Zhang, Y. Li, X. M. Wang and X. D. Zhang, “MPSOMNR Algorithm Study of 2-D Electrical Impedance Tomography,” Computer Engineering and Applications, Vol. 49, No. 3, 2013, pp. 29-32.
- M. Donelli and A. Massa, “Computational Approach Based on a Particle Swarm Optimizer for Microwave Imaging of Two-Dimensional Dielectric Scatterers,” IEEE Transactions on Microwave Theory and Techniques, Vol. 53, No. 5, 2005, pp. 1761-1776. http://dx.doi.org/10.1109/TMTT.2005.847068
- S. Huang, “Regularization Algorithm Research of Static Electrical Impedance Tomography,” Ph.D. Dissertation, Chongqing University, Chongqing, 2005.
NOTES
*Supported by special foundation of education department of Shaanxi provincial government (No. 2010JK892), national college’s student innovative project (No. 201210722024).

