Open Journal of Biophysics
Vol.3 No.2(2013), Article ID:30140,15 pages DOI:10.4236/ojbiphy.2013.32017
Systems Approach to Mitotic Chromosome Motions
Rutgers, The State University of New Jersey, Camden, USA
Email: gagliard@camden.rutgers.edu
Copyright © 2013 Lucian John Gagliardi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 21, 2012; revised January 27, 2013; accepted February 9, 2013
Keywords: Mitotic Chromosome Motions; Systems Approach; Ndc80/Hec1; Electrostatic Force
ABSTRACT
Recent experiments revealing possible nanoscale electrostatic interactions in force generation at kinetochores for chromosome motions have prompted speculation regarding possible models for interactions between positively charged molecules in kinetochores and negative charge on C-termini near the plus ends of microtubules. A clear picture of how kinetochores establish and maintain a dynamic coupling to microtubules for force generation during the complex motions of mitosis remains elusive. The molecular cell biology paradigm requires that specific molecules, or molecular geometries, for force generation be identified. However, it is possible to account for mitotic chromosome motions within a systems approach in terms of experimentally known cellular electric charge distributions interacting over nanometer distances.
1. Introduction
Mitotic motions and events can be described within a systems approach in terms of cellular electric charge distributions. Mitotic motions are seen here as an emergent property of the pHi-dependent dynamic instability of microtubules at the balanced state, in combination with nanoscale electrostatic interactions between 1) microtubules and kinetochores; 2) microtubules and centro some matrices; and 3) microtubules and chromosome arms. A major advantage of this approach is that it appears to offer the possibility of discovering a minimal assumptions model for post-attachment chromosome motions. Current thought on mitotic motions is shifting to a more electrostatics based framework [1,2], perhaps in line with theoretical predictions made almost a decade ago [3,4].
Chromosome movement is dependent on kinetochoremicrotubule dynamics: a chromosome can move toward a pole only when its kinetochore is connected to microtubules emanating from that pole [5]. Microtubules continually assemble and disassemble, so the turnover of tubulin is ongoing. The characteristics of microtubule lengthening (polymerization) and shortening (depolymerization) follow a pattern known as “dynamic instability”, that is, at any given instant some of the microtubules are growing, while others are undergoing rapid breakdown. In general, the rate at which microtubules undergo net assembly—or disassembly—varies with mitotic stage [6]. It is proposed in this paper that changes in chromosome motions during mitosis can be attributed to changes in microtubule dynamics. It is further proposed that the influence of intracellular pH changes on kinetochore microtubule dynamics—in conjunction with nanoscale electrostatic interactions between microtubule free ends and charge distributions at kinetochores, centrosomes, and chromosome arms—is primarily responsible for post-attachment prometaphase and metaphase chromosome motions. These aspects will be described here within a systems biology approach to mitotic motions and events.
2. Some Cellular Electrostatics
In the cytoplasmic medium (cytosol) within biological cells, it has been generally thought that electrostatic fields are subject to strong attenuation by screening with oppositely charged ions (counterion screening), decreasing exponentially to much smaller values over a distance of several Debye lengths. The Debye length within cells is typically given to be of order 1 nm [7], and since cells of interest in the present work (i.e. eukaryotic) have much larger dimensions, one would be tempted to conclude that electrostatic force could not be a major factor in providing the cause for mitotic chromosome movements in biological cells. However, the presence of microtubules, as well as other factors to be discussed shortly, change the picture completely.
Microtubules can be thought of as intermediaries that extend the reach of the electrostatic interaction over cellular distances, making this second most potent force in the universe available to cells in spite of their ionic nature. Microtubules are 25 nm diameter cylindrical structures comprised of protofilaments, each consisting of tubulin dimer subunits, 8 nm in length, aligned end to end parallel to the microtubule axis. The protofilaments are bound laterally to form a cylindrical microtubule. The structure of microtubules is similar in all eukaryotic cells. Cross sections reveal that the wall of a microtubule consists of a circle of 4 to 5 nm diameter subunits. The circle typically contains 13 subunits as observed in vivo; however, 11, 12, 14, or 16 have also been observed. Neighboring dimers along protofilaments exhibit a small (Blattice) offset of 0.92 nm from protofilament to protofilament. This offset will be approximated as 1 nm in the calculations in Section 4 since protofilament curling distributions for disassembling microtubules are more significant in determining the distances of protofilament free ends from various cellular structures such as kinetochores and centrosome matrices.
It has been experimentally determined that there are differences in the profiles of growing and shrinking microtubules. Assembling and disassembling microtubules are depicted in Figure 1.
Experiments have shown that the intracellular pH (pHi) of many cells rises to a maximum at the onset of mitosis, subsequently falling steadily during later stages [8,9]. Although it is experimentally difficult to resolve the exact starting time for the beginning of the decrease in pHi during the cell cycle, it appears to decrease 0.3 to 0.5 pH units from the typical peak values of 7.3 to 7.5 measured earlier during prophase [8].
Studies [10] have shown that in vivo microtubule growth (polymerization) is favored by higher pH values. It should be noted that in vitro studies of the role of pH in regulating microtubule assembly indicate a pH optimum for assembly in the range of 6.3 to 6.7. The disagreement between in vitro and in vivo studies has been analyzed in relation to the nucleation potential of microtubule organizing centers like centrosomes [10], and it has been suggested that pHi regulates the nucleation potential of microtubule organizing centers [11-13]. In addition, ionic strength differences between cells and in vitro media must be taken into account [14]. This favors the more complex physiology characteristic of in vivo studies to resolve this question. It will therefore be assumed here that in vivo experimental design is more appropriate for experiments relating to pH conditions affecting microtubule assembly.
A number of investigations have focused on the electrostatic properties of microtubule tubulin subunits [15- 18]. Large scale calculations of the tubulin molecule
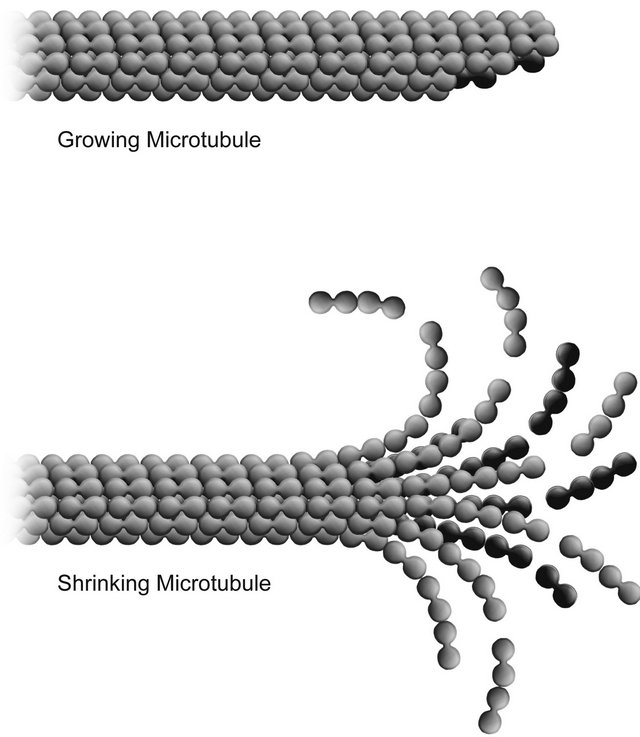
Figure 1. Shrinking (showing protofilament curling) and growing microtubules.
have been carried out using molecular dynamics programs along with protein parameter sets. The dipole moment of tubulin has been calculated to be as large as 1800 Debye (D) [16,19]. Experiments [20] have shown that tubulin net charge depends strongly on pH, varying quite linearly from −12 to −28 (electron charges) between pH 5.5 and 8.0. This could be significant for tubulin electrostatics during mitosis because, as noted above, a number of cell types exhibit a decrease of 0.3 to 0.5 pH units from a peak at prophase during mitosis.
It has been determined that tubulin has a large overall negative charge of 20 at pH 7, and that as much as 40% of the charge resides on C-termini. The C-termini can point nearly perpendicularly outward from the microtubule axis as a strong function of pHi, extending 4 - 5 nm at pHi 7 [21]. It would seem reasonable to assume that an increased tubulin charge and the resulting greater negative charge and extension of C-termini may be integral to an increased probability for microtubule assembly during prophase when pHi is highest. A higher pHi during prophase is consistent with increased interaction between the highly extended C-termini of tubulin dimers with appropriate regions of other nearest neighbor dimers.
Given the observed decrease in pHi during mitosis, changes in microtubule assembly probabilities—in conjunction with nanoscale electrostatic interactions—could be responsible for the observed changes in chromosome motions during mitosis. In particular, a decrease in pHi during mitosis may act as a master clock controlling microtubule disassembly to assembly (disassembly/assembly) probability ratios during the phases of mitosis, thereby controlling the timing and dynamics of mitotic chromosome movements through metaphase. This will be discussed in more detail in Section 5 after the necessary groundwork has been developed.
Experiments [22] have revealed that mitotic spindles can assemble around DNA-coated beads incubated in Xenopus egg extracts. Since the phosphate groups of the DNA will manifest a net negative charge at the pH of this experimental system, I have postulated that pericentriolar material—the centrosome matrix within which the microtubule dimer dipolar subunits assemble in many cell types to form asters [23]—carries a net negative charge [3,24]. Centrosomes have subsequently been shown to have a net negative charge by direct measurement [25].
Thus given the electric dipole nature of microtubule subunits and the efficiency of aster self assembly, it is likely that microtubule minus ends proximal to centrosomes are positively charged with plus free ends negatively charged. (According to existing convention, rapidly growing microtubule free ends are designated plus and the slower growing free ends are designated minus, there being no reference to charge in the use of this nomenclature.) This assignment of the signs of the net charge at microtubule free ends is consistent with 1) large scale computer calculations of tubulin dimer subunits showing that 18 positively charged calcium ions are bound within  monomers, with an equal number of negative charges localized at adjacent
monomers, with an equal number of negative charges localized at adjacent 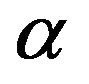 monomers [15, 16]; and 2) experiments revealing that microtubule plus ends terminate with a crown of
monomers [15, 16]; and 2) experiments revealing that microtubule plus ends terminate with a crown of 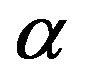 subunits and minus ends terminate with
subunits and minus ends terminate with  subunits [26]; 3) the lower pH vicinal to a negatively charged centrosome matrix will cause a greater expression of positive charge on microtubule free minus ends and the higher pH vicinal to a positively charged kinetochore pole-facing “plate” will cause a greater expression of negative charge on microtubule free plus ends; 4) negative charge on centrosome matrices will induce positive charge on microtubule minus ends and positive charge at pole-facing plates of kinetochores will induce negative charge on microtubule plus ends.
subunits [26]; 3) the lower pH vicinal to a negatively charged centrosome matrix will cause a greater expression of positive charge on microtubule free minus ends and the higher pH vicinal to a positively charged kinetochore pole-facing “plate” will cause a greater expression of negative charge on microtubule free plus ends; 4) negative charge on centrosome matrices will induce positive charge on microtubule minus ends and positive charge at pole-facing plates of kinetochores will induce negative charge on microtubule plus ends.
In 2002 and 2005 papers, I argued that indirect experimental evidence indicates that pole-facing “plates” of kinetochores exhibit positive charge [3,4,24] and interact with negatively charged microtubule free plus ends to provide the motive force at kinetochores for poleward chromosome motions. This has been supported by experiments [1,2,27] implicating positively charged kinetochore molecules (e.g., Ndc80/Hec1) in establishing a dynamic coupling to negative charge on microtubule plus ends during mitosis.
As will be discussed shortly, quite apart from the ability of microtubules to extend electrostatic interactions over cellular distances, the range of electrostatic fields within the cytosol itself is longer than ordinary counterion screening considerations would dictate. These electrostatic conditions will be seen throughout the present work to have important implications for the events of mitosis.
Evidence for positive charge at kinetochores also comes from the presence of highly basic molecules in the Dam1 complex. In particular, the isoelectric points of Dam1p, Duo1p, and Spc34p are 9.97, 10.76, and 8.6, respectively. Significantly, experiments have revealed that the microtubule binding module of the Dam1 complex involves these three molecules; acidic proteins Ask1p, Spc19p, and Dad2p fail to bind [28].
3. Spindle Assembly and Dynamics
It is reasonable to expect that the electric dipole nature of tubulin subunits greatly assists in their self-assembly into the microtubules of the asters and spindle. Thus we may envision that electrostatic fields organize and align the electric dipole dimer subunits, thereby facilitating their assembly into the microtubules that form the asters and mitotic spindle [24]. This self-assembly would be aided by significantly reduced counterion screening due to layered water adhering to the net charge of the dipolar subunits. Such water layering to charged proteins has long been theorized [29,30] and has been confirmed by experiment [31]. Additionally, as will be discussed in Section 4.1, layered water between sufficiently close charged proteins has a dielectric constant that is considerably reduced from the bulk value far from charged surfaces, further increasing the tendency for an electrostatic assist to aster and spindle self-assembly. The question of what is meant by “sufficiently close” charged protein surfaces as well as the reduction in the dielectric constant between such surfaces will be addressed in Section 4.1.
The combination of these two effects (or conditions)—water layering and reduced dielectric constant— can significantly influence cellular electrostatics in a number of important ways related to cell division. It will be convenient in the present work to characterize gaps between charged surfaces within cells that allow these two effects to significantly enhance electrostatic interactions as critical separations or critical distances (see Section 4.1). These conditions would be expected to significantly increase the efficiency of microtubule selfassembly in asters and spindles by 1) allowing electrostatic interactions over greater distances than Debye screening dictates; and 2) increasing the strength of these interactions by an order of magnitude due to a corresponding order of magnitude reduction in the cytosolic dielectric constant between charged protein surfaces separated by critical distances or less.
As we will see in subsequent sections, these two effects for charged molecular surfaces at close range may also have important consequences regarding force generation for chromosome motions and other mitotic events.
As mentioned above, measurements have shown that pHi of many cells rises to a maximum at the onset of mitosis and subsequently decreases throughout cell division. This could account for the efficient self-assembly of the spindle during prophase, when microtubule polymerization and microtubule organizing center nucleation is favored because of the greater expression of negative charge on tubulin dimers and centrosome matrices due to the higher pHi at this time.
An electrostatic component to the biochemistry of the microtubules in assembling asters is consistent with experimental observations of pH effects on microtubule assembly [10], as well as the sensitivity of microtubule stability to calcium ion concentrations [32,33]. Thus it would seem reasonable to assume that, over distances consistent with the modified counterion screening discussed above, the electrostatic nature of tubulin dimers would allow tubulin dimer microtubule subunits 1) to be attracted to and align around charge distributions within cells—in particular, as mentioned above, around centrosomes; and 2) to align end to end and laterally, facilitating the formation of asters and mitotic spindles.
The motive force for the migration of asters and assembling half-spindles during prophase can also be addressed in terms of nanoscale electrostatics. As a consequence of the negative charge on the free plus ends of microtubules at the periphery of the forming asters/ half-spindles, the asters/half-spindles would be electrostatically repelled from each other and drift apart. Specifically, as microtubule assembly proceeds, a subset of the negatively charged microtubule free ends at the periphery of one of the growing asters/half-spindles would mutually repel a subset of the negatively charged free ends within critical distances at the periphery of the other, causing them to drift apart as net microtubule assembly proceeds. Such subsets will be continually changing as poleward migration of the asters/half-spindles continues [24].
As discussed above, because of significantly reduced counterion screening and the low dielectric constant of layered water adhering to the tubulin dimers, the necessary interaction and alignment of tubulin molecules during spindle self-assembly would be enhanced by the considerably increased range and strength of the electrostatic attraction between oppositely charged regions of tubulin dimers.
Similarly, the mutually repulsive electrostatic force between subsets of interacting negatively charged microtubule free ends from opposing half-spindles in the growing mitotic spindle would be expected to be significantly increased in magnitude and range. An instantaneous subset of interacting microtubules in a small portion of a forming spindle is depicted in Figure 2. Thus mutual electrostatic repulsion of negatively charged microtubule free plus ends distal to centrosomes in assembling asters/ half-spindles could provide the driving force for their poleward migration in the forming spindle [24]. It is important to note that subsets of interacting microtubules from opposing half-spindles can result from either growing or shrinking microtubules, but—as discussed above— polymerization probabilities will dominate during prophase. This process would continue until growing halfspindles drift as far apart as possible, establishing the cell poles.
It seems clear that cellular electrostatics involves more than the traditional thinking regarding counterion screening of electric fields and the resulting unimportance within cells of the second most powerful force in nature. The reality may be that the evidence suggests otherwise, and that the resulting enhanced electrostatic interactions are more robust and act over greater distances than previously thought. One aspect of this is the ability of microtubules to extend the reach of electrostatic force over cellular distances; another lies in the reduced counterion sceeening and dielectric constant of the cytosol between charged protein surfaces.
High pHi during prophase favors spindle assembly. This includes greater electrostatic attractive forces between tubulin dimers as well as increased repulsive electrostatic interactions driving poleward movements of forming half-spindles.
Changes in microtubule dynamics are integral to changes in the motions of chromosomes during mitosis. These changes in microtubule dynamics can be attributed to an associated change in intracellular pH (pHi) during mitosis. In particular, a decrease in pHi during mitosis may act as a master clock controlling microtubule disassembly/assembly probability ratios by altering the
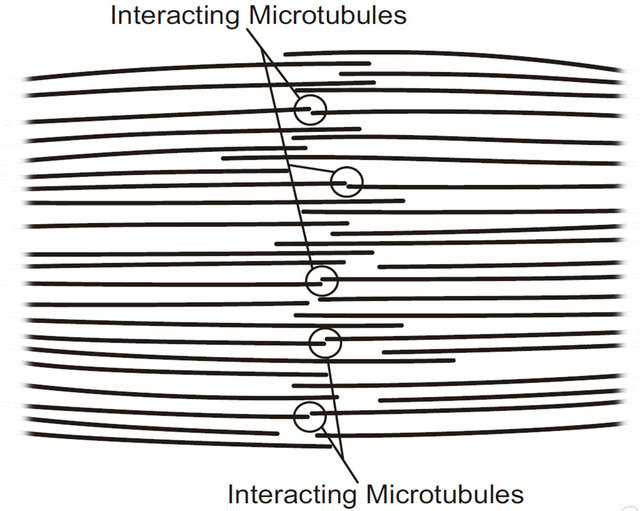
Figure 2. A subset of interacting microtubules in a small portion of a forming mitotic spindle. The free plus ends of interacting microtubules within a few nanometers are mutually repelling. Protofilament curling of disassembling microtubules is not shown on this scale.
electrostatic interactions of tubulin dimers. As will be discussed in Section 5, this may determine the timing and dynamics of post-attachment mitotic chromosome motions.
4. Electrostatic Force in Poleward Chromosome Motions
4.1. Electrostatic Microtubule Disassembly Force at Cell Poles
From the discussion in Section 2, the net charge on the free ends of microtubules at a centrosome matrix is assumed to be positive. A γ-tubulin molecule, embedded in the fibrous centrosome matrix, takes the form of a ring from which a microtubule appears to emerge [34]. This would allow the electric field of the negatively charged centrosome matrix to draw the positively charged ends of microtubules into the centrosome matrix, with the resulting rapid change of the electric field just outside and across the outer boundary of the centrosome matrix destabilizing microtubules as they pass into the charge distribution.
Thus γ-tubulin rings may be regarded as forming a firmly anchored negative charge distribution near the surface of a centrosome matrix through which microtubules pass, disassembling in the passage, as depicted in Figure 3.
As in the case for a kinetochore (discussed later), the
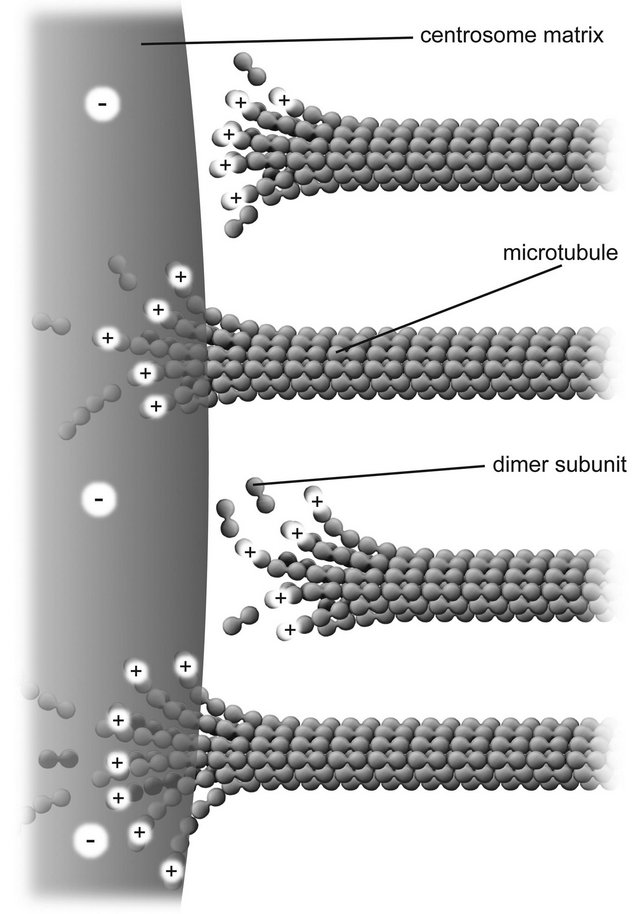
Figure 3. Nanoscale electrostatic disassembly force at a centrosome. A poleward force results from an electrostatic attraction between positively charged microtubule free ends and an oppositely charged centrosome matrix. Only disassembling microtubules are depicted; assembling microtubules could also be momentarily attracted to a centrosome.
microtubules do not necessarily need to pass through the rings; rather, the rings provide a structurally stable negatively charged volume distribution attracting microtubules to and into the centrosome matrix.
As noted above, observations on a number of cell types have shown that disassembly of microtubules at spindle poles accompanies chromosome poleward movement. Accordingly, within the context of the present work, force generation at spindle poles for prometaphase post-attachment, metaphase, and anaphase-A poleward chromosome motions can be attributed to an electrostatic attraction between the positively charged free minus ends of kinetochore microtubules and a negatively charged centrosome matrix.
We now calculate the magnitude of the force produced in this manner by a non-penetrating microtubule at a centrosome matrix. Since the outer diameter of a centrosome matrix is considerably larger than the diameter of a microtubule, we may model it as a large, approximately planar slab with negative surface charge density of magnitude  as depicted in Figure 3. From the wellknown Debye-Hückel result for a planar charged surface with area charge density
as depicted in Figure 3. From the wellknown Debye-Hückel result for a planar charged surface with area charge density  immersed in an electrolyte [35], we have for the electrostatic potential
immersed in an electrolyte [35], we have for the electrostatic potential
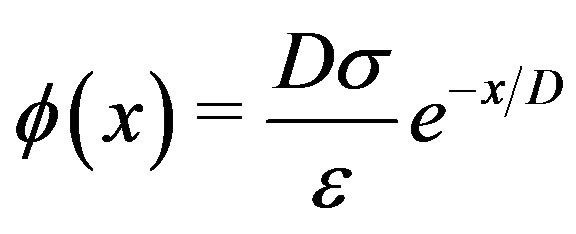 , (1)
, (1)
where  is the Debye length and
is the Debye length and 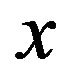 is the distance from the surface.
is the distance from the surface.
The electric field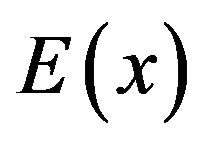 , obtained from the negative gradient of the electrostatic potential, multiplied by the charge
, obtained from the negative gradient of the electrostatic potential, multiplied by the charge 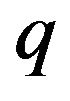 gives the magnitude of the attractive force
gives the magnitude of the attractive force 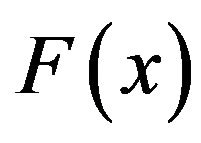 between the charge
between the charge 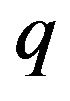 on a dimer subunit at the end of a protofilament and the centrosome. This results in
on a dimer subunit at the end of a protofilament and the centrosome. This results in
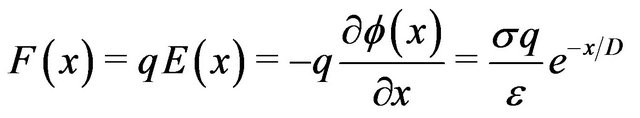 . (2)
. (2)
It is well established in electrochemistry [36] that the permittivity of the first few water layers outside a charged surface is an order of magnitude smaller than that of the bulk phase. The effective permittivity of water as a function of distance from a charged surface has been determined by atomic force microscopy [37] to increase monotonically from 4 - 6 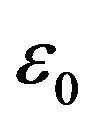 at the interface to 78
at the interface to 78 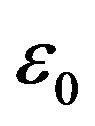 at a distance of 25 nm from the interface. The values of the dielectric constants
at a distance of 25 nm from the interface. The values of the dielectric constants 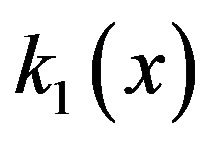 at distances of 1, 2, 3, and 4 nm from a charged surface were measured to be 9, 21, 40, and 60, respectively. As discussed in Section 3, layered water adhering to the net charge of proteins will significantly reduce counterion screening for small distances from the surface.
at distances of 1, 2, 3, and 4 nm from a charged surface were measured to be 9, 21, 40, and 60, respectively. As discussed in Section 3, layered water adhering to the net charge of proteins will significantly reduce counterion screening for small distances from the surface.
The interpolated values of 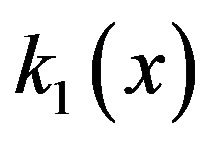 for separations between charged surfaces of up to 3 nm are 5, 9, 9, and 5 for x = 0, 1, 2, and 3 respectively, where the charged surfaces are at x = 0 and x = 3 nm. The distance range 1 to 3 nm between charged surfaces is significant for the present calculation because 1 nm may be taken as the thickness of layered water adsorbed to each charged surface [30,38], and for charged surface separations up to 3 nm, counterion screening would be virtually eliminated. Thus for charged surfaces at separations of 3 nm or less, the exponential decay of the electric field from each surface reduces the electric field to a minimum of approximately 60% of the maximum value at each surface and, to a good approximation, Debye screening can be neglected. For brevity in subsequent discussions, separations of 0 to 3 nm between charged surfaces will be designated as critical separations. The electrostatic potential energy
for separations between charged surfaces of up to 3 nm are 5, 9, 9, and 5 for x = 0, 1, 2, and 3 respectively, where the charged surfaces are at x = 0 and x = 3 nm. The distance range 1 to 3 nm between charged surfaces is significant for the present calculation because 1 nm may be taken as the thickness of layered water adsorbed to each charged surface [30,38], and for charged surface separations up to 3 nm, counterion screening would be virtually eliminated. Thus for charged surfaces at separations of 3 nm or less, the exponential decay of the electric field from each surface reduces the electric field to a minimum of approximately 60% of the maximum value at each surface and, to a good approximation, Debye screening can be neglected. For brevity in subsequent discussions, separations of 0 to 3 nm between charged surfaces will be designated as critical separations. The electrostatic potential energy 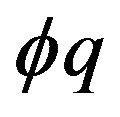 between charged surfaces separated by 5 nm is near the upper limit of the effective range within which thermal energy is less than electrostatic energy for a charge
between charged surfaces separated by 5 nm is near the upper limit of the effective range within which thermal energy is less than electrostatic energy for a charge 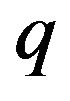 of one electron charge.
of one electron charge.
For critical separations, the expression for the force between a charged centrosome matrix surface at x = 0 and a charge 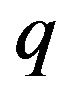 on the free minus end of a protofilament at a distance x from the surface may therefore be written
on the free minus end of a protofilament at a distance x from the surface may therefore be written
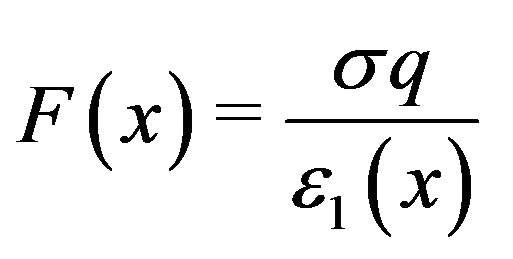 , (3)
, (3)
where  is obtained from the interpolated experimental results for
is obtained from the interpolated experimental results for  referred to above,
referred to above, 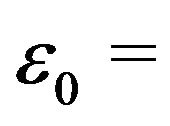 8.85 pF/m and q is the charge on the protofilament free end. This equation may be obtained from (2) in the limit as
8.85 pF/m and q is the charge on the protofilament free end. This equation may be obtained from (2) in the limit as , a condition that effectively eliminates counterion screening.
, a condition that effectively eliminates counterion screening.
There are 13 protofilaments arranged circularly in a microtubule, with an axial shift of 0.92 nm for each protofilament as one moves around the circumference of a B lattice microtubule [16]. For comparison with experimental values, a calculation of the maximum disassembly force per microtubule will be carried out for 3 protofilaments with their free ends at distances of 1, 2, and 3 nm from the centrosome matrix surface. The actual distribution for the distances of the free ends of 13— disassembling (curling), and temporarily assembling (straight)—protofilaments would be considerably complicated, and it is probable that more than 3 protofilaments will interact with a centrosome matrix within critical distances.
As mentioned above, experimental values of surface charge density  for biological surfaces range from 1 to 50 mC/m2. Thus, we may sum the forces on protofilament free ends at distances of 1, 2, and 3 nm from the centrosome matrix using the above interpolated values of
for biological surfaces range from 1 to 50 mC/m2. Thus, we may sum the forces on protofilament free ends at distances of 1, 2, and 3 nm from the centrosome matrix using the above interpolated values of 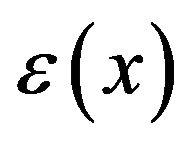 and a conservative value for
and a conservative value for  of 10 mC/m2. Carrying out this calculation with (3), we find that the electrostatic force sums to
of 10 mC/m2. Carrying out this calculation with (3), we find that the electrostatic force sums to  pN/MT (picoNewtons per microtubule), where
pN/MT (picoNewtons per microtubule), where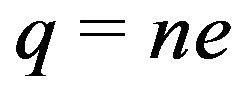 , with e equal to the magnitude of the charge on an electron and n the number of electron charges at a protofilament free end. Comparing this value with the experimental range of 1 - 74 pN/MT [39] for the maximum tension force per microtubule, we have that n = 0.04 - 3.2 electron charges. This range of values compares favorably to experiments [16, 18,40], and the agreement represents a successful ab initio theoretical derivation of the magnitude of this force. We now proceed to calculate the electrostatic force on a kinetochore due to penetrating microtubules.
, with e equal to the magnitude of the charge on an electron and n the number of electron charges at a protofilament free end. Comparing this value with the experimental range of 1 - 74 pN/MT [39] for the maximum tension force per microtubule, we have that n = 0.04 - 3.2 electron charges. This range of values compares favorably to experiments [16, 18,40], and the agreement represents a successful ab initio theoretical derivation of the magnitude of this force. We now proceed to calculate the electrostatic force on a kinetochore due to penetrating microtubules.
4.2. Electrostatic Microtubule Disassembly Force at Kinetochores
Experimental observations on force generation at kinetochores may also be addressed using electrostatics. As discussed above, kinetochore pole-facing surfaces manifest positive charge. Assuming a volume positive charge at kinetochore pole-facing surfaces, we may envision a mechanism for electrostatic force generation at kinetochores by penetrating microtubules. It has been accepted for some time that electron microscope studies show kinetochore microtubules running uninterupted between poles and kinetochores, terminating in the outer poleward-facing plate of the kinetochores [41]. It has also been assumed that this kinetochore-microtubule association is the locus of force generation. As a result, ultrastructural studies of kinetochore-microtubule associations have concentrated on the microtubules that are apparently penetrating the outer plate of kinetochores, and possibly being pulled into kinetochores by interactions between kinetochores and kinetochore microtubules to produce poleward force.
These interactions have been described in more specific terms in the recent literature, and may be classified as being based on motor molecules [42], or binding relationships between protofilaments and kinetochore molecules [43,44]. As mentioned in Section 1, experiments have recently revealed that kinetochore-microtubule binding is dependent on electrostatic interactions mediated via positive charge in the disordered N-terminal 80 amino acid tail domain of Hec1 [1,2], an observation that is in agreement with the approach presented here.
Since kinetochore plate diameters are large compared to the diameters of protofilaments, we may model the kinetochore-microtubule interaction for penetrating microtubules by assuming an approximately planar slab of uniform positive charge density, with thickness a parallel to the x axis for the outer kinetochore plate interacting with negatively charged free ends of microtubule protofilaments, as depicted in Figure 4.
The possibility of binding to kinetochore molecules, or Dam1 rings around microtubules, is not assumed in favor of a more general approach wherein interacting kinetochore molecules comprise a positive charge distribution
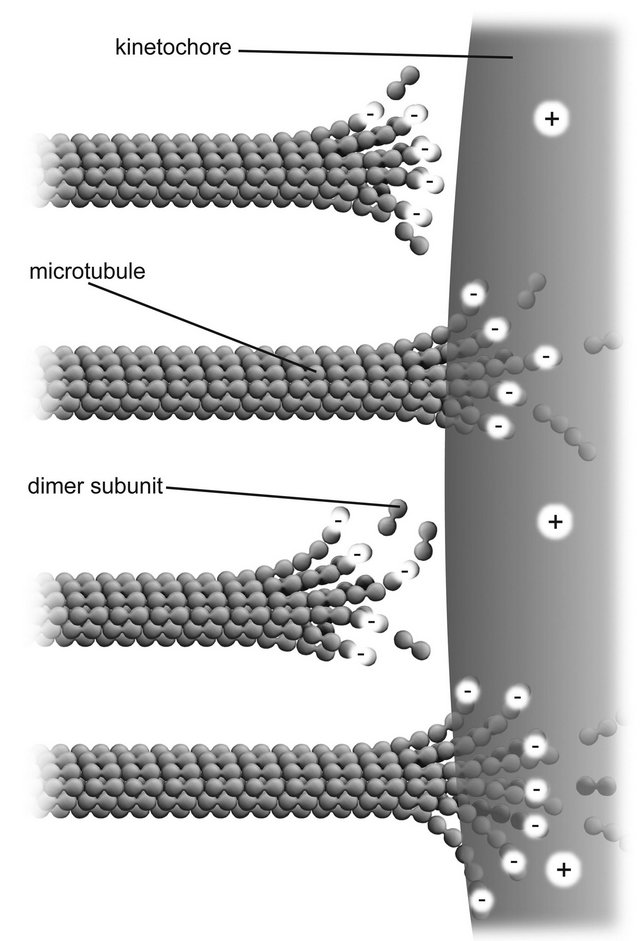
Figure 4. Nanoscale electrostatic disassembly force at a charged kinetochore. A poleward force results from an electrostatic attraction between negatively charged microtubule free ends and an oppositely charged kinetochore. Only disassembling microtubules are depicted; assembling microtubules could also be momentarily attracted to a centrosome.
through which microtubule-bound negative charges at or near the free plus ends of kinetochore microtubules are drawn.
A standard result from an application of Gauss’s law [45] gives the following result for the electric field inside a large, uniformly charged slab of positive charge
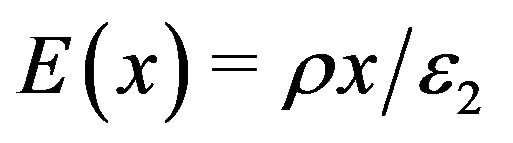 , (4)
, (4)
where  is the volume charge density,
is the volume charge density, 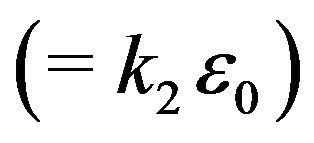
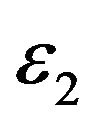 is the dielectric permittivity of the slab, and
is the dielectric permittivity of the slab, and 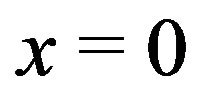 at the plane of symmetry in the center of the large rectangular slab. (Note that previously in (3),
at the plane of symmetry in the center of the large rectangular slab. (Note that previously in (3), 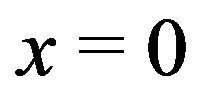 at the right boundary of the centrosome matrix, Figure 3.)
at the right boundary of the centrosome matrix, Figure 3.)
Making use of the uniform charge relation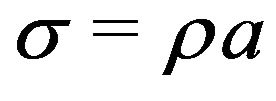 , this result may be expressed in terms of the surface charge density
, this result may be expressed in terms of the surface charge density  as
as
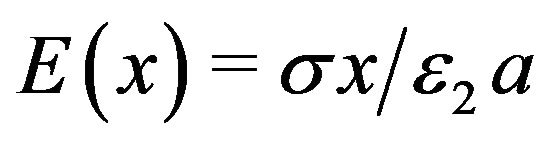 . (5)
. (5)
Electron microscope studies reveal that kinetochore microtubules penetrate only the outer (poleward-facing) plate on each kinetochore [41]. The magnitude of the force on a protofilament of negative charge magnitude 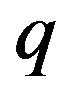 at its free end a distance x from the outer plate’s plane of symmetry is given by
at its free end a distance x from the outer plate’s plane of symmetry is given by
 . (6)
. (6)
At the left face of the kinetochore (Figure 4), 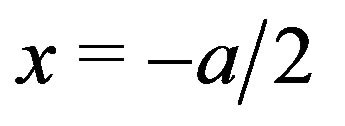 , and
, and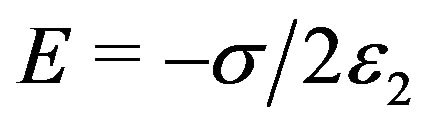 , and the force exerted in the negative
, and the force exerted in the negative 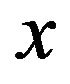 (poleward) direction on a kinetochore by a protofilament free end with negative charge of magnitude
(poleward) direction on a kinetochore by a protofilament free end with negative charge of magnitude 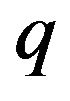 at its free end located just inside the left face is
at its free end located just inside the left face is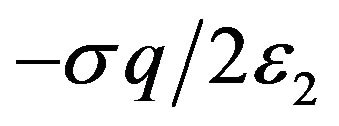 .
.
The value of the dielectric constant 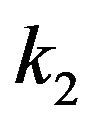 for a kinetochore has not been established. Consistent with their open structures, a cytosol-saturated kinetochore or centrosome matrix would be expected to have a dielectric constant that is quite large, roughly midway between their dry values and that of cytoplasmic water [46]. As with a centrosome matrix, 1) the value for cytoplasmic water will dominate; and 2) the calculation is relatively insensitive to the precise dry value. From these considerations,
for a kinetochore has not been established. Consistent with their open structures, a cytosol-saturated kinetochore or centrosome matrix would be expected to have a dielectric constant that is quite large, roughly midway between their dry values and that of cytoplasmic water [46]. As with a centrosome matrix, 1) the value for cytoplasmic water will dominate; and 2) the calculation is relatively insensitive to the precise dry value. From these considerations, 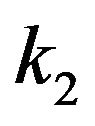 can be taken as 30.
can be taken as 30.
Using 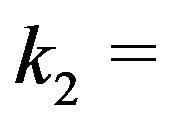 30 and the value
30 and the value 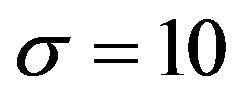 mC/m2 in carrying out a conservative calculation for a microtubule with 6 of the 13 protofilament ends—irrespective of protofilament curling—at an average distance
mC/m2 in carrying out a conservative calculation for a microtubule with 6 of the 13 protofilament ends—irrespective of protofilament curling—at an average distance 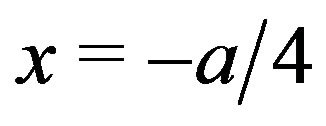 from the symmetry plane,
from the symmetry plane,  (where the force is 0), we find that the force on a penetrating microtubule sums to 90n pN/MT. Equating this result to the experimental range 1 - 74 pN/MT, we find that n = 0.01 - 0.82 electron charges, again well within the experimental range.
(where the force is 0), we find that the force on a penetrating microtubule sums to 90n pN/MT. Equating this result to the experimental range 1 - 74 pN/MT, we find that n = 0.01 - 0.82 electron charges, again well within the experimental range.
An evaluation of the force on a kinetochore from a non penetrating microtubule within a critical distance of the kinetochore mirrors the previous calculation for a centrosome matrix. As mentioned above, it has generally been assumed that penetrating kinetochore microtubules are responsible for force generation. Consequently not much attention has been given to the possibility that kinetochore microtubules may be generating force in non-contact interactions such as those arising from electrostatics.
Force generation by nanoscale electrostatic non-contact interactions, primarily over critical separations, would cause other (previously force-generating) kinetochore microtubules in the bundle to penetrate the kinetochore, giving the illusion of contact force generation by penetration. Importantly, forces acting at nanometer distances would seem to be essential for efficient microtubule reattachment and tracking to kinetochores throughout mitosis, a feature that is not addressed by any of the current models for chromosome motility. The present model assumes that force generation is due to both penetrating and non-penetrating microtubules.
As in the case for poleward force generation at a centrosome, non-penetrating microtubules that disassemble in the region of high electric field gradient just outside the outer plate of a charged kinetochore also generate a poleward force, as depicted in Figure 4. Because of the similarity in geometry, a calculation of the force per microtubule for non-penetrating microtubules at kinetochores will yield essentially the same result as the calculation at a centrosome. Accordingly, a force calculation with (3) carried out with 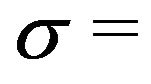 10 mC/m2 also reproduces the experimental range 1 - 74 pN/MT as the nanoscale electrostatic microtubule disassembly force at a kinetochore for the experimentally verified charge range of 0.04 to 3.2 electron charges at a protofilament free end.
10 mC/m2 also reproduces the experimental range 1 - 74 pN/MT as the nanoscale electrostatic microtubule disassembly force at a kinetochore for the experimentally verified charge range of 0.04 to 3.2 electron charges at a protofilament free end.
As mentioned earlier, given the electric dipole nature as well as the large overall net charge on C-termini of tubulin microtubule subunits, the electric field gradient over a critical separation distance within vicinal cytosol at a centrosome matrix or kinetochore would act to destabilize the microtubules. In addition, the field gradient across either boundary can destabilize microtubules, further increasing the depolymerization probability for microtubules approaching and penetrating these structures as force is generated, in agreement with observation.
These gradients will now be quantified. To gain perspective (since electric fields and electric field gradients are less intuitive) it will be convenient to calculate force gradients. For the electrostatic force gradient in the vicinal cytosol at a kinetochore or centrosome matrix, we may consider a protofilament free end with one electron charge e starting at a distance of 1 nm where the dielectric constant is 9, then moving to the surface where the dielectric constant is 5 (see interpolated values of 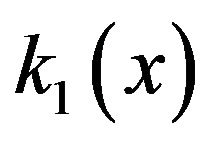 given in Section 4.1). From x = 1 to 0, we have a force increase
given in Section 4.1). From x = 1 to 0, we have a force increase 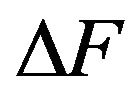 of
of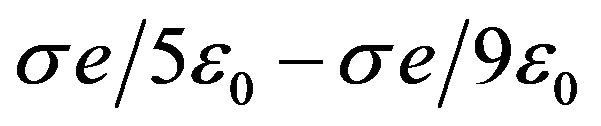 . Evaluating the average force gradient,
. Evaluating the average force gradient,  over the separation distance
over the separation distance 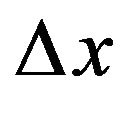 = 1 nm, we have that
= 1 nm, we have that 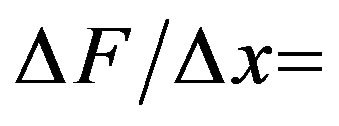 166 pN/nm. This is a rather large average force gradient. Similarly, the average gradient over 2 nm experienced by a protofilament free end with one electron charge penetrating a centrosome matrix or kinetochore boundary where the force changes from
166 pN/nm. This is a rather large average force gradient. Similarly, the average gradient over 2 nm experienced by a protofilament free end with one electron charge penetrating a centrosome matrix or kinetochore boundary where the force changes from  to
to 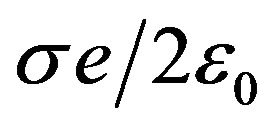 is 160 pN/nm.
is 160 pN/nm.
4.3. Penetrating Microtubules at a Centrosome
To complete the possibilities for poleward force production, we now consider the situation for microtubules penetrating a centrosome matrix. The value of the dielectric constant  for a centrosome matrix has also not been established. As discussed above for a kinetochore, due to an open structure that allows cytoplasmic water intrusion, the large dielectric constant of water would strongly influence the overall dielectric constant of the centrosome matrix, leading to a value that is relatively insensitive to the dry value. As discussed previously, consistent with their open structures, a cytosol-saturated centrosome matrix or kinetochore would be expected to have a dielectric constant that is quite large, again roughly midway between their dry values and cytoplasmic water. Therefore, as with a kinetochore, 1) the value for cytoplasmic water will dominate; and 2) the calculation is relatively insensitive to the precise dry value. For simplicity, the conservative value
for a centrosome matrix has also not been established. As discussed above for a kinetochore, due to an open structure that allows cytoplasmic water intrusion, the large dielectric constant of water would strongly influence the overall dielectric constant of the centrosome matrix, leading to a value that is relatively insensitive to the dry value. As discussed previously, consistent with their open structures, a cytosol-saturated centrosome matrix or kinetochore would be expected to have a dielectric constant that is quite large, again roughly midway between their dry values and cytoplasmic water. Therefore, as with a kinetochore, 1) the value for cytoplasmic water will dominate; and 2) the calculation is relatively insensitive to the precise dry value. For simplicity, the conservative value 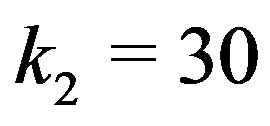 will again be assumed.
will again be assumed.
In the above force calculation at a kinetochore, the possibility that molecules of the Dam1 complex can form rings around microtubules was not considered fundamental. Instead, a more general approach considered kinetochore molecules as contributing a structurally stable positive charge distribution that negatively charged microtubule plus ends can be attracted to and drawn into. Similarly, 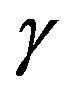 -tubulin rings may be viewed as a firmly anchored negative charge distribution through which the positively charged minus ends of kinetochore microtubules are drawn, generating poleward force associated with an observed poleward microtubule flux.
-tubulin rings may be viewed as a firmly anchored negative charge distribution through which the positively charged minus ends of kinetochore microtubules are drawn, generating poleward force associated with an observed poleward microtubule flux.
As a result of these similarities, and the assumed approximate equality of 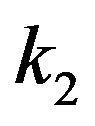 for both a kinetochore and a centrosome matrix, a calculation of the poleward force per microtubule for penetrating microtubules at a centrosome matrix will yield a result identical to the above calculation at a kinetochore. As in all the calculations in Section 4, since the calculated range of
for both a kinetochore and a centrosome matrix, a calculation of the poleward force per microtubule for penetrating microtubules at a centrosome matrix will yield a result identical to the above calculation at a kinetochore. As in all the calculations in Section 4, since the calculated range of 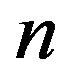 is well within the experimental range, moderate differences in
is well within the experimental range, moderate differences in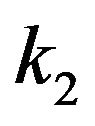 , the geometry, and other contributing factors would not be significant.
, the geometry, and other contributing factors would not be significant.
5. Operation of the Model
5.1. Introduction
Poleward and antipoleward chromosome movements occur intermittently during prometaphase and metaphase. Antipoleward motions dominate during the congressional movement of chromosomes to the cell equator. Poleward motion of chromosomes dominates during anaphase-A. The apparent complexity of these motions has challenged scientific explanation for over a hundred years. While a number of models have been advanced for individual motions, such as anaphase-A, it can be argued that the various motions are related, and that a simple theme or principle that unifies mitotic motions should be sought. It is proposed in this work that this can be accomplished within a systems approach by attributing the cause for post-attachment chromosome motions to microtubule dynamics in combination with nanoscale electrostatics.
Experiments [47] have shown that during prometaphase each pair of sister chromatids attaches by a kinetochore to the outside walls of a single microtubule, resulting in a rapid microtubule sidewall sliding movement toward a pole. This motion is postulated to be driven by molecular motors. A molecular motor-powered microtubule sidewall sliding model for this prometaphase movement would appear likely. In particular, the speed (20 - 50 μm per minute) [48] of kinetochores along microtubule walls is consistent with known molecular motor behavior. However post-attachment prometaphaseas well as metaphase, chromosome motions can be understood in terms of a cell-cycle dependent increase in the dominance of nanoscale electrostatic microtubule disassembly forces due to a steadily decreasing pHi.
As discussed elsewhere [49], force generation by induced negative charge on plus ends and induced positive charge on minus ends of microtubules could also be responsible for poleward force generation. Although a calculation of the induced positive charge on microtubule minus ends from negative charge on a centrosome matrix is difficult because of the complex geometry, a reciprocal calculation of induced negative charge on a centrosome matrix from positive charge at minus ends of microtubules is relatively straightforward and agrees with the experimental range of force per microtubule measurements [49]. Similarly a reciprocal calculation of induced positive charge on a kinetochore due to negative charge at free plus ends of microtubules also falls within the force per microtubule experimental range [49].
Antipoleward nanoscale microtubule assembly forces will now be considered. As a result of the sliding capture motion described above, the approach to the poles will result in the movement of kinetochores to within critical distances from the ends of other (astral) microtubules emanating from the closer pole. As discussed in previous sections, counterion screening is not fully operative for separation distances of 3 nm or less. The resulting proximity-in conjunction with 1) an electrostatic attraction between positively charged kinetochores and the negatively charged ends of astral microtubules; 2) an electrostatic repulsion between negatively charged chromosome arms in the chromatid pair and other negatively charged astral microtubule ends; and 3) constant thermal agitation, could be critical in the orientation and end-on attachment of kinetochores to the free plus ends of microtubules [3].
Following this monovalent (or mono-oriented) attachment to one pole, chromosomes are observed to move at considerably slower speeds, a few μm per minute, in subsequent motions throughout prometaphase [48]. In particular, a period of slow motions toward and away from a pole will ensue, until close proximity of the free end of a microtubule from the opposite pole with the other (sister) kinetochore in the chromatid pair results in an attachment to both poles (a bivalent (bioriented) attachment). Attachments of additional microtubules from both poles will follow. (There may have been additional attachments to the first pole before any attachment to the second.)
After a sister kinetochore becomes attached to microtubules from the opposite pole, the chromosomes perform a slow (1 - 2 μm per minute) congressional motion to the spindle equator, resulting in the well-known metaphase alignment of chromatid pairs. In addition to the mechanism facilitating attachment just discussed, all of the above mentioned experimentally observed postattachment poleward and antipoleward prometaphase motions, as well as metaphase oscillatory motion, can be understood in terms of electrostatic interactions coupled with pHi-dependent microtubule dynamics.
5.2. Antipoleward Nanoscale Electrostatic Assembly Force
Since chromosome arms are negatively charged, following chromosome attachment they will be repelled from the negatively charged free ends of the shorter astral microtubules in the polar region. As mentioned above and discussed in Section 4.1, this force will be effective over the critical distances allowed by modified Debye screening. As astral microtubules assemble, and chromosomes move farther from the poles, there will be a filling in of dipolar subunits in the gaps between the astral microtubule free ends and chromosome arms.
Polymerization will take place in the gaps opened up by electrostatic repulsion between negatively charged microtubule free plus ends and negatively charged chromosome arms as they drift farther from the poles, and chromosomes will be continuously repelled from the poles. This mechanism may account for the antipoleward astral exclusion force, or polar wind, the precise nature of which has been sought since it was first observed [50]. The interaction between astral microtubules and chromosome arms is depicted in Figure 5.
As a chromatid pair moves farther from a pole, electrostatic repulsive force between the negatively charged free ends of astral microtubules and chromosomes will decrease as the microtubules fan radially outward.
At a surface defined by the microtubule ends, the charge density and therefore the force, will decrease ac cording to an “inverse square law,” as we can see from
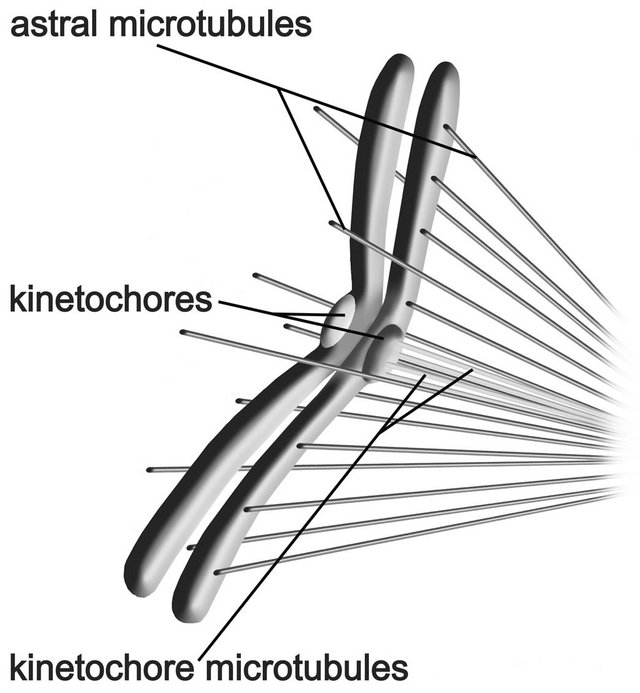
Figure 5. Antipoleward nanoscale electrostatic force between microtubules and chromosome arms. An antipoleward force results from electrostatic repulsion between negatively charged plus ends of microtubules and negatively charged chromosome arms.
the following. Given that the repulsive force on a chromosome arm depends on the total number 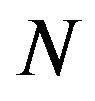 of negatively charged microtubule free ends from which it is repelled, we have that F is proportional to Nq, where
of negatively charged microtubule free ends from which it is repelled, we have that F is proportional to Nq, where 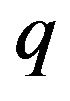 is the charge at the end of a microtubule.
is the charge at the end of a microtubule.
For N microtubules fanning radially outward from a pole, the total charge Nq is distributed over an area that increases as the distance r from the pole squared (r2), and the effective charge per unit area at a surface defined by the microtubule ends decreases as the inverse of the distance squared (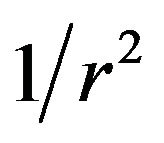 ). This results in an electrostatic antipoleward force on chromosome arms that decreases with an inverse square (
). This results in an electrostatic antipoleward force on chromosome arms that decreases with an inverse square (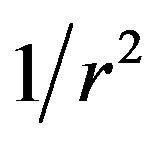 ) dependence on the polar distance.
) dependence on the polar distance.
The falloff is expected to be even more pronounced than inverse square would predict because of the decreased number of microtubule free ends at greater polar distances, as shown schematically in Figure 6, resulting in an even stronger falloff of antipoleward force with distance from cell poles. To save writing, this stronger than inverse square falloff will be characterized as robust inverse square.
5.3. Prometaphase and Metaphase Chromosome Motions
As cited in Section 2, experiments have shown that the intracellular pH (pHi) of many cell types rises to a maximum during prophase, subsequently falling steadily through mitosis. The continuing decrease in pHi through metaphase [8] would result in an increasing instability of the microtubules comprising the spindle fibers. In Section 2, I noted that in vivo experiments have shown that microtubule stability is related to pHi, with a more basic pH favoring microtubule assembly. An increased probability for microtubule depolymerization—as compared
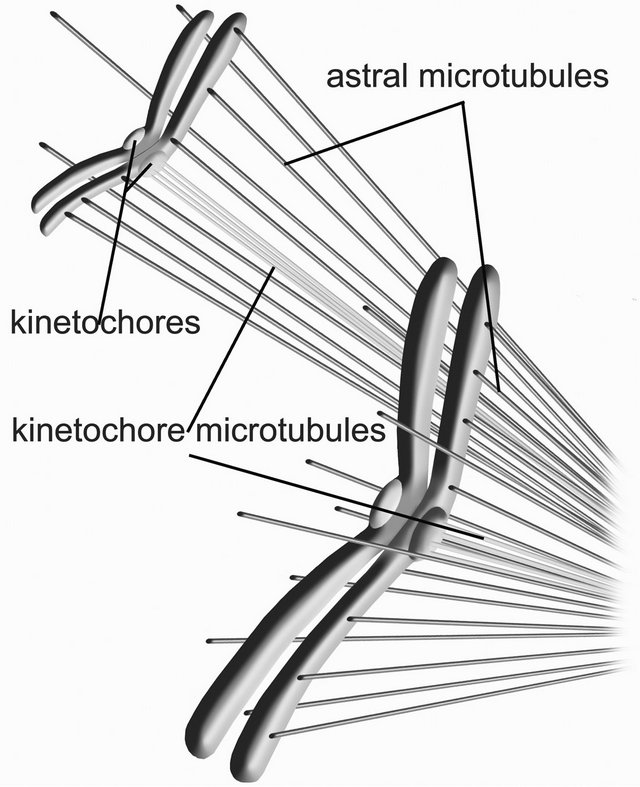
Figure 6. Antipoleward inverse square repulsive force. Two chromatid pairs at differing polar distances are depicted showing the robust inverse square dependence of the nanoscale antipoleward force.
to the prophase predominance of microtubule assembly—is consistent with the observed alternating poleward and antipoleward motions of monovalently attached chromosomes during prometaphase.
Thus microtubule polymerization and depolymerization, in combination with a repulsive electrostatic antipoleward astral exclusion force and an attractive electrostatic poleward directed force acting at kinetochores and spindle poles, is sufficient to account for the observed motion of monovalently attached chromosomes. Because of statistical fluctuations both in the number of disassembling kinetochore microtubules interacting with kinetochores as well as centrosomes, and in the number of assembling astral microtubules responsible for the antipoleward force acting at chromosome arms, the interaction of these opposing forces would result in a “tug of war,” consistent with the experimentally observed series of movements toward and away from a pole for a monovalently attached chromatid pair.
After a bivalent attachment has been established, the attractive force to the far (distal) pole will be in opposition to the attractive force to the near (proximal) pole. Because of the robust inverse square astral exclusion force, the greater repulsion from the proximal pole, along with a growing number of kinetochore attachments to microtubules from the distal pole tending to equalize poleward disassembly forces, a relatively sustained congressional motion away from the proximal pole would result, as observed experimentally.
As a chromatid pair moves farther from the proximal pole, there will be a growing number of attachments to both poles. Following approximately equal numbers of attachments to both poles, and comparable distances of a chromatid pair from the two poles, the forces exerted by both sets of poleward attractive disassembly and antipoleward repulsive assembly forces will approach equality. As a chromatid pair congresses to the midcell region, the number of attachments to both poles will tend to be the same, as will the number of microtubules interacting with chromosome arms, and equilibrium of poleward directed forces as well as antipoleward astral exclusion forces will be approached. Without specifying their exact nature, balanced pairs of attractive and repulsive forces have previously been postulated for the metaphase alignment of chromatid pairs [51].
An explanation of experimentally observed metaphase oscillations about the cell equator just prior to anaphase-A provides another example of the predictability and minimal assumptions nature of the present approach. In agreement with experiment [52], the present model predicts that the poleward force on a chromosome from kinetochore microtubule disassembly at kinetochores and poles depends on the total number of kinetochore microtubules. At the metaphase “plate,” the bivalent attachment of chromatid pairs ensures that the poleward- directed electrostatic disassembly force on one chromatid at a given moment could be greater than that at the sister chromatid’s kinetochore attached to the opposite pole. An imbalance of these poleward forces results from statistical fluctuations in the number of force generating microtubules at kinetochores as well as at poles.
This situation, coupled with similar fluctuations in the number of astral microtubules responsible for the antipoleward astral exclusion force on a chromatid pair, can result in a momentary motion toward a pole in the direction of the instantaneous net electrostatic force. However, because of the robust inverse square dependence of the repulsive astral exclusion force and the approximate equality of poleward-directed microtubule disassembly forces for chromatid pairs in the midcell region, the greater force of repulsion from the proximal pole will eventually reverse the direction of motion, resulting in stable equilibrium midcell metaphase oscillations, as observed experimentally.
Midcell metaphase oscillations are direct experimental evidence for a continuing increase in the disassembly/ assembly probability ratio resulting in parity for microtubule assembly and disassembly probabilities.
At late metaphase, before anaphase-A, experiments reveal that the poleward motions of sister kinetochores stretch the intervening centromeric chromatin, producing high kinetochore tensions. It is reasonable to attribute these high tensions to a continuing disassembly to assembly probability ratio increase caused by a further lowering of pHi. The resulting attendant increase in poleward electrostatic disassembly force would lead to increased tension. A lower pHi will also increase the expression of positive charge on sister kinetochores, further elevating the tension due to their increased mutual repulsion. At these high tensions, microtubule plus ends often switch from a depolymerization state to a polymerization state of dynamic instability. This may be explained by kinetochore microtubule free ends passively taking up the slack by polymerization to sustain attachment and resist further centromeric chromatin stretching. This is known as the “slip-clutch mechanism” [53].
This mechanism is addressed within the context of the present work as follows. Microtubule assembly at a kinetochore or pole is regarded here as operating in passive response to 1) the robust inverse square electrostatic antipoleward force acting between the plus ends of astral microtubules and chromosome arms and/or; 2) an electrostatic microtubule disassembly force at a sister kinetochore or at poles. At the highest tensions, non-contact electrostatic forces acting over a range of protofilament free end-kinetochore distances would be effective in helping to maintain coupling while other larger protofilament gaps in the same or other microtubules are passively filled in. This process would continue with new gaps and new opportunities for fill-in. In addition, the repulsive robust inverse square electrostatic assembly force acting at the sister chromatid’s arms would provide a positive feedback mechanism to resist detachment. This explanation of the slip-clutch mechanism follows as a direct consequence of the present systems approach to chromosome motility. The slip-clutch mechanism does not appear to be addressed within any of the models for chromosome motions in the current literature.
It should be noted that microtubule assembly at kinetochores and poles can occur; however because the necessary inverse square dependence of the antipoleward microtubule assembly force cannot be derived from microtubule assembly at kinetochores or spindle poles, it is assumed in the present work that assembly at either location is in passive stochastic response to assembly at chromosome arms, or to tension caused by poleward force on sister kinetochores.
Thus regarding post-attachment chromosome movements through metaphase, it seems reasonable to ascribe the increasing microtubule dissassembly/assembly probability ratio—with attendant changes in microtubule dynamics and mitotic chromosome motions—to an experimentally observed steadily decreasing pHi. We may then envision the decrease in pHi from a peak at prophase favoring microtubule (and spindle) assembly, declining through prometaphase, and continuing to decline through metaphase when parity between microtubule assembly and disassembly leads to midcell chromatid pair oscillations, culminating in increased kinetochore disassembly tension near anaphase, as a cell’s master clock controlling microtubule dynamics, and consequently the events of mitosis. One might also attribute the more complete dominance of microtubule disassembly—with an accompanying predominance of poleward electrostatic disassembly forces—during anaphase-A to a further continuation of a decreasing intracellular pH. However, as we now discuss, additional possible decreases in pHi during anaphase-A may work in conjunction with a microtubule destabilizing [Ca2+] increase.
5.4. Anaphase-A Chromosome Motion
Chromosome motion during anaphase has two major components, designated anaphase-A and anaphase-B. Anaphase-A is concerned with the poleward motion of chromosomes, accompanied by the shortening of kinetochore microtubules at kinetochores and/or spindle poles. The second component, referred to as anaphase-B involves the separation of cell poles as the cause for the further separation of chromosomes and is treated elsewhere [54]. As discussed above, antipoleward electrostatic forces compete stochastically with poleward electrostatic forces during prometaphase and metaphase. For example, after a bivalent attachment is established, the action of poleward-directed forces from both poles, in conjunction with the robust inverse square nature of the antipoleward force, is sufficient for congressional motion to the cell equator followed by midcell metaphase chromosome oscillations. As also discussed above, these oscillations result from robust inverse square antipoleward electrostatic assembly forces at chromosome arms acting in conjunction with approximately balanced poleward electrostatic disassembly forces. This balance is changed by subsequent events as will now be discussed.
In a number of cell types, intracellular calcium releases show a temporal correlation with the onset of anaphase-A. Experimental studies have shown that intracellular [Ca2+] increases are associated with anaphase-A chromosome movement [55-57]. It is well known that increased [Ca2+] facilitates the depolymerization of spindle microtubules both in vitro [58] and in vivo [59]. These experimental observations have a direct interpretation within the framework of electrostatic force generating mechanisms.
With the observed increase in [Ca2+] and the resulting further increase in the instability of microtubules, the disassembly to assembly probability ratio will be increased even more. After chromatid separation heralds the beginning of anaphase-A, the increased disassembly/assembly probability ratio allows nanoscale electrostatic microtubule disassembly forces at kinetochores and poles to dominate, enabling the dynamics for anaphase-A chromosome movement.
Given that kinetochores exhibit a net positive charge and will manifest an even greater positive charge at lower pHi levels in late metaphase, the resulting increased expression of charge on kinetochores, coupled with their close proximity and the inverse square nature of the Coulomb electrostatic force—acting in combination with increased electrostatic microtubule disassembly force tension from kinetochores and poles—could supply sufficient force to initiate chromatid separation. This is consistent with the observed increased kinetochore tension close to the metaphase-anaphase transition discussed above.
Studies have shown that changes in [Ca2+] can modulate the speed of chromosome motion [57,60]. Significantly, there appears to be an optimum concentration for maximizing the speed of chromosome motions during anaphase-A. If [Ca2+] is increased to a micromolar level, anaphase-A chromosome motion is increased two-fold above the control rate; however, if the concentration is further increased beyond a few micromolar, the chromosomes will slow down, and possibly stop [57]. It has long been recognized that one way elevated [Ca2+] could increase the speed of chromosome motion during anaphase-A is by facilitating microtubule depolymerization
[32, 58-61], and it is commonly believed that the breakdown of microtubules, if not the motor for chromosome motion, is at least the rate-determining step [62-65]. However, the slowing or stopping of chromosome motion associated with moderate increases beyond an optimum [Ca2+] is more difficult to interpret since the microtubule network of the spindle is not compromised to the extent that anaphase-A chromosome motion could be slowed or stopped; this would require considerably higher concentrations [57,66].
Experimental observation that an increase in calcium levels beyond micromolar levels results in a slowing or stopping of anaphase-A motion is a direct consequence of an electrostatic motor for mitotic chromosome motions. Higher concentrations of doubly charged calcium ions would screen the negative charge at the free ends of disassembling kinetochore microtubules and at the centrosome matrix, shutting down the poleward-directed nanoscale electrostatic disassembly force. Since this happens at concentrations that do not compromise the spindle’s microtubule network, it is reasonable to interpret these results as experimentally consistent with an electrostatic microtubule disassembly force at kinetochores and cell poles.
An experimental test of nonspecific divalent cation effects on anaphase-A chromosome motion in which Mg was substituted for Ca2+ [57] does not offer a definitive test for the possibility of negative charge cancellation by positive ions. The reason is that the positive charge of Mg is shielded much more effectively by water than is the case for Ca2+. This is shown by high frequency sound absorption studies of substitution rate constants for water molecules in the inner hydration shell of various ions which reveal that the inner hydration shell water substitution rate for Mg is more than three orders of magnitude slower than that for Ca2+ [67]. Thus the slowing or stopping of anaphase-A chromosome motion accompanying free calcium concentration increases above the optimum concentration for maximum anaphase-A chromosome speed—but well below concentration levels that compromise the mitotic apparatus—is consistent with an electrostatic disassembly motor for poleward chromosome motions. This experimental result has not been addressed by any of the current models for anaphase-A motion.
5.5. Conclusion
Post-attachment chromosome motions during prometaphase and metaphase can be explained by nanoscale electrostatic microtubule antipoleward assembly forces acting between microtubules and chromosome arms, combined with nanoscale electrostatic microtubule poleward disassembly forces acting at kinetochores and spindle poles. The shift from the dominance of microtubule growth during prophase, and to a lesser extent during prometaphase, to a parity between microtubule polymerization and depolymerization during metaphase chromosome oscillations, can be attributed to an increase in the microtubule disassembly to assembly probability ratio due to the gradual downward pHi shift during mitosis that is observed in many cell types.
The factors: 1) an intracellular pH decrease continuing through mitosis; 2) an electrostatic component to microtubule disassembly/assembly probability ratios; 3) a nanoscale electrostatic microtubule disassembly force acting at kinetochores and centrosome matrices; and 4) a nanoscale electrostatic microtubule assembly force acting between negatively charged microtubule plus ends and like charged chromosome arms, all working in conjunction with microtubule dynamics, make it possible to explain the motive force—and timing—for chromosome motions throughout post-attachment prometaphase and metaphase within the context of a systems approach to mitotic chromosome motions.
The observed intracellular increase in [Ca2+] that occurs in conjunction with anaphase-A further increases the domination of poleward microtubule disassembly forces over antipoleward microtubule assembly forces. The superiority of poleward microtubule disassembly forces combined with an increased mutual repulsion of positively charged sister kinetochores—with both due to a decreased pHi—could be integral in the initial separation of sister chromatids. Once this separation is effected, anaphase-A motion would result from the predominance of electrostatic microtubule disassembly forces at kinetochores and poles.
REFERENCES
- G. J. Guimaraes, Y. Dong, B. F. McEwen and J. G. DeLuca, “Kinetochore-Microtubule Attachment Relies on the Disordered N-Terminal Tail Domain of Hec1,” Current Biology, Vol. 18, No. 22, 2008, pp. 1778-1784. doi:10.1016/j.cub.2008.08.012
- S. A. Miller, M. L. Johnson and P. T. Stukenberg, “Kinetochore Attachments Require an Interaction between Unstructured Tails on Microtubules and Ndc80/Hec1,” Current Biology, Vol. 18, No. 22, 2008, pp. 1785-1791. doi:10.1016/j.cub.2008.11.007
- L. J. Gagliardi, “Electrostatic Force in Prometaphase, Metaphase, and Anaphase-A Chromosome Motions,” Physical Review E, Vol. 66, No. 1, 2002, Article ID: 011901.
- L. J. Gagliardi, “Electrostatic Force Generation in Chromosome Motions during Mitosis,” Journal of Electrostatics, Vol. 63, No. 3-4, 2005, pp. 309-327. doi:10.1016/j.elstat.2004.09.007
- R. B. Nicklas and D. F. Kubai, “Microtubules, Chromosome Movement, and Reorientation after Chromosomes Are Detached from the Spindle by Micromanipulation,” Chromosoma, Vol. 92, No. 4, 1985, pp. 313-324. doi:10.1007/BF00329815
- B. Alberts, D. Bray, J. Lewis, M. Raff, M. K. Roberts and J. D. Watson, “Molecular Biology of the Cell,” Garland Publishing Company, New York, 1994, p. 920.
- G. B. Benedek and F. M. H. Villars, “Physics: With Illustrative Examples from Medicine and Biology: Electricity and Magnetism,” Springer-Verlag, New York, 2000, p. 403.
- R. A. Steinhardt and M. Morisawa, “Changes in Intracellular pH of Physarum Plasmodium during the Cell Cycle and in Response to Starvation,” In: R. Nuccitelli and D. W. Deamer, Eds., Intracellular pH: Its Measurement, Regulation, and Utilization in Cellular Functions, Alan R. Liss, New York, 1982, pp. 361-374.
- C. Amirand, et al., “Intracellular pH in One-Cell Mouse Embryo Differs between Subcellular Compartments and Between Interphase and Mitosis,” Biology of Cell, Vol. 92, No. 6, 2000, pp. 409-419. doi:10.1016/S0248-4900(00)01080-7
- G. Schatten, T. Bestor, R. Balczon, J. Henson and H. Schatten, “Intracellular pH Shift Leads to Microtubule Assembly and Microtubule-Mediated Motility during Sea Urchin Fertilization: Correlations between Elevated Intracellular pH, Microtubule Activity and Depressed Intracellular pH and Microtubule Disassembly,” European Journal of Cell Biology, Vol. 36, No. 1, 1985, pp. 116- 127.
- M. W. Kirschner, “Implications of Treadmilling for the Stability and Polarity of Actin and Tubulin Polymers in Vivo,” Journal of Cell Biology, Vol. 86, No. 1, 1980, pp. 330-334. doi:10.1083/jcb.86.1.330
- M. De Brabander, G. Geuens and R. Nuydens, “Microtubule Stability and Assembly in Living Cells: The Influence of Metabolic Inhibitors, Taxol and pH,” Cold Spring Harbor Symposia on Quantitative Biology, Vol. 46, 1982, pp. 227-240. doi:10.1101/SQB.1982.046.01.026
- W. J. Deery and B. R. Brinkley, “Cytoplasmic Microtubule Assembly—Disassembly from Endogenous Tubulin in a Brij-Lysed Cell Model,” Journal of Cell Biology, Vol. 96, No. 6, 1983, pp. 1631-1641. doi:10.1083/jcb.96.6.1631
- J. B. Olmsted and G. G. Borisy, “Characterization of Microtubule Assembly in Porcine Brain Extracts by Viscometry,” Biochemistry, Vol. 12, No. 21, 1973, pp. 4282- 4289. doi:10.1021/bi00745a037
- M. V. Satarić, J. A. Tuszyński and R. B. Žakula, “Kinklike Excitations as an Energy Transfer Mechanism in Microtubules,” Physical Review E, Vol. 48, No. 1, 1993, pp. 589-597. doi:10.1103/PhysRevE.48.589
- J. A. Brown and J. A. Tuszyński, “Dipole Interactions in Axonal Microtubules as a Mechanism of Signal Propagation,” Physical Review E, Vol. 56, No. 5, 1997, pp. 5834- 5840. doi:10.1103/PhysRevE.56.5834
- N. A. Baker, D. Sept, S. Joseph, M. J. Holst and J. A. McCammon, “Electrostatics of Nanosystems: Applications to Microtubules and the Ribosome,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 98, No. 18, 2001, pp. 10037-10041. doi:10.1073/pnas.181342398
- J. A. Tuszyński, J. A. Brown and P. Hawrylak, “Dielectric Polarization, Electrical Conduction, Information Processing and Quantum Computation in Microtubules: Are They Plausible?” Philosophical Transactions of the Royal Society of London, Vol. A356, No. 1743, 1998, pp. 1897- 1926.
- J. A. Tuszyński, S. Hameroff, M. V. Satarić, B. Trpisová, and M. L. A. Nip, “Ferroelectric Behavior in Microtubule Dipole Lattices: Implications for Information Processing, Signaling and Assembly/Disassembly,” Journal of Theoretical Biology, Vol. 174, No. 4, 1995, pp. 371-380. doi:10.1006/jtbi.1995.0105
- D. Sackett, “pH-Induced Conformational Changes in the Carboxy Terminal Tails of Tubulin,” Presented at the Banff Workshop Molecular Biophysics of the Cytoskeleton, Banff, 25-30 August 1997.
- J. A. Tuszyński, J. A. Brown, E. J. Carpenter and E. Crawford, “Electrostatic Properties of Tubulin and Microtubules,” In: J. M. Crowley, Ed., Proceedings of the Electrostatics Society of America and Institute of Electrostatics Japan, Laplacian Press, Morgan Hill, 2002, pp. 41-50.
- R. Heald, R. Tournebize, T. Blank, R. Sandaltzopoulos, P. Becker, A. Hyman and E. Karsenti, “Self-Organization of Microtubules into Bipolar Spindles around Artificial Chromosomes in Xenopus Egg Extracts,” Nature, Vol. 382, 1996, pp. 420-425. doi:10.1038/382420a0
- H. C. Joshi, M. J. Palacios, L. McNamara, D. W. Cleveland, “γ-Tubulin Is a Centrosomal Protein Required for Cell Cycle-Dependent Microtubule Nucleation,” Nature, Vol. 356, 1992, pp. 80-83. doi:10.1038/356080a0
- L. J. Gagliardi, “Microscale Electrostatics in Mitosis,” Journal of Electrostatics, Vol. 54, No. 3-4, 2002, pp. 219- 232. doi:10.1016/S0304-3886(01)00155-3
- S. Hormeño, et al., “Single Centrosome Manipulation Reveals Its Electric Charge and Associated Dynamic Structure,” Biophysical Journal, Vol. 97, No. 4, 2009, pp. 1022-1030. doi:10.1016/j.bpj.2009.06.004
- Y. H. Song and E. Mandelkow, “The Anatomy of Flagellar Microtubules: Polarity, Seam, Junctions, and Lattice,” Journal of Cell Biology, Vol. 128, No. 1, 1995, pp. 81-94. doi:10.1083/jcb.128.1.81
- C. Ciferri, et al., “Implications for Kinetochore-Microtubule Attachment from the Structure of an Engineered Ndc80 Complex,” Cell, Vol. 133, No. 3, 2008, pp. 427- 439. doi:10.1016/j.cell.2008.03.020
- S. Westermann, et al., “Formation of a Dynamic Kinetochore-Microtubule Interface through Assembly of the Dam1 Ring Complex,” Molecular Cell, Vol. 17, No. 2, 2005, pp. 277-290. doi:10.1016/j.molcel.2004.12.019
- D. Jordan-Lloyd and A. Shore, “The Chemistry of Proteins,” J. A. Churchill Publishing Company, London, 1938.
- L. Pauling, “The Adsorption of Water by Proteins,” Journal of American Chemical Society, Vol. 67, No. 4, 1945, pp. 555-557. doi:10.1021/ja01220a017
- M. F. Toney, J. N. Howard, J. Richer, G. L. Borges, J. G. Gordon, O. R. Melroy, D. G. Wiesler, D. Yee and L. Sorensen, “Voltage-Dependent Ordering of Water Molecules at an Electrode-Electrolyte Interface,” Nature, Vol. 368, 1994, pp. 444-446. doi:10.1038/368444a0
- R. C. Weisenberg, “Microtubule Formation in Vitro in Solutions Containing Low Calcium Concentrations,” Science, Vol. 177, No. 4054, 1972, pp. 1104-1105. doi:10.1126/science.177.4054.1104
- G. G. Borisy and J. B. Olmsted, “Nucleated Assembly of Microtubules in Porcine Brain Extracts,” Science, Vol. 177, No. 4055, 1972, pp. 1196-1197. doi:10.1126/science.177.4055.1196
- B. Alberts, D. Bray, J. Lewis, M. Raff, M. K. Roberts and J. D. Watson, “Molecular Biology of the Cell,” Garland Publishing Company, New York, 1994, p. 930.
- G. B. Benedek and F. M. H. Villars, “Physics: With Illustrative Examples from Medicine and Biology: Electricity and Magnetism,” Springer-Verlag, New York, 2000, p. 400.
- J. O. Bockris and A. K. N. Reddy, “Modern Electrochemistry,” Plenum Press, New York, 1977. doi:10.1007/978-1-4613-4136-9
- O. Teschke, G. Ceotto and E. F. de Souza, “Interfacial Water Dielectric Permittivity Profile Measurements Using Atomic Force Microscopy,” Physical Review E, Vol. 64, No. 1, 2001, Article ID: 011605.
- G. H. Pollack, “Cells, Gels and the Engines of Life,” Ebner and Sons Publishers, Seattle, 2001, p. 69.
- S. P. Alexander and C. L. Rieder, “Chromosome Motion during Attachment to the Vertebrate Spindle: Initial Saltatory-Like Behavior of Chromosomes and Quantitative Analysis of Force Production by Nascent Kinetochore Fibers,” The Journal of Cell Biology, Vol. 113, No. 4, 1991, pp. 805-815. doi:10.1083/jcb.113.4.805
- R. Stracke, K. J. Böhm, L. Wollweber, J. A. Tuszynski and E. Unger, “Analysis of the Migration Behaviour of Single Microtubules in Electric Fields,” Biochemical and Biophysical Research Communications, Vol. 293, No. 1, 2002, pp. 602-609.
- C. L. Rieder, “The Formation, Structure, and Composition of the Mammaliam Kinetochore and Kinetochore Fiber,” International Review of Cytology, Vol. 79, 1982, pp. 1-58. doi:10.1016/S0074-7696(08)61672-1
- G. Civelekoglu-Scholey, D. J. Sharp, A. Mogilner and J. M. Scholey, “Model of Chromosome Motility in Drosophila Embryos: Adaptation of a General Mechanism for Rapid Mitosis,” Biophysical Journal, Vol. 90, No. 11, 2006, pp. 3966-3982. doi:10.1529/biophysj.105.078691
- E. L. Grishchuk et al., “The Dam1 Ring Binds Microtubules Strongly Enough to Be a Processive as Well as Energy-Efficient Coupler for Chromosome Motion,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 105, No. 40, 2008, pp. 15423-15428. doi:10.1073/pnas.0807859105
- J. R. McIntosh, et al., “Kinetochore-Microtubule Interactions Visualized by EM Tomagraphy,” The 47th Annual Meeting of the American Society for Cell Biology, Washington DC, 1-5 December 2007.
- D. J. Griffiths, “Introduction to Electrodynamics,” Prentice-Hall Publishing Company, Upper Saddle River, 1999, p. 75.
- S. A. Schelkunoff, “Electromagnetic Fields,” Blaisdell Publishing Company, New York, 1963, p. 29.
- C. L. Rieder and S. P. Alexander, “Kinetochores Are Transported Poleward along a Single Astral Microtubule during Chromosomes Attachment to the Spindle in Newt Lung Cells,” The Journal of Cell Biology, Vol. 110, No. 1, 1990, pp. 81-95. doi:10.1083/jcb.110.1.81
- A. Grancell and P. K. Sorger, “Chromosome Movement: Kinetochores Motor Along,” Current Biology, Vol. 8, No. 11, 1998, pp. R382-R385. doi:10.1016/S0960-9822(98)70243-X
- L. J. Gagliardi, “Induced Electrostatic Charge in Poleward Motion of Chromosomes during Mitosis,” Journal of Electrostatics, Vol. 66, No. 3-4, 2008, pp. 147-155. doi:10.1016/j.elstat.2007.11.002
- C. L. Rieder, E. A. Davison and L. C. W. Jensen, “Oscillatory Movements of Monooriented Chromosomes and Their Position Relative to the Spindle Pole Result from the Ejection Properties of the Aster and Half-Spindle,” The Journal of Cell Biology, Vol. 103, No. 2, 1986, pp. 581-591. doi:10.1083/jcb.103.2.581
- B. Alberts, D. Bray, J. Lewis, M. Raff, M. K. Roberts and J. D. Watson, “Molecular Biology of the Cell,” Garland Publishing Company, New York, 1994, p. 926.
- T. S. Hays and E. D. Salmon, “Poleward Force at Kinetochores in Metaphase Depends on the Number of Kinetochore Microtubules,” The Journal of Cell Biology, Vol. 110, No. 2, 1990, pp. 391-404. doi:10.1083/jcb.110.2.391
- H. Maiato, J. DeLuca, E. D. Salmon and W. C. Earnshaw, “The Dynamic Kinetochore-Microtubule Interface,” Journal of Cell Science, Vol. 117, Part 23, 2004, pp. 5461- 5477. doi:10.1242/jcs.01536
- L. J. Gagliardi, “Electrostatic Considerations in Mitosis,” iUniverse Publishing Company, Bloomington, 2009.
- P. K. Hepler and D. A. Callaham “Free Calcium Increases in Anaphase in Stamen Hair Cells of Tradescantia,” The Journal of Cell Biology, Vol. 105, No. 5, 1987, pp. 2137- 2143. doi:10.1083/jcb.105.5.2137
- P. K. Hepler, “Regulation of Anaphase Spindle Microtubule Structure in Stamen Hair Cells of Tradescantia by Calcium and Related Agents,” In: J. S. Hyams and B. R. Brinkley, Eds., Mitosis: Molecules and Mechanisms, Academic Press, San Diego, 1989, pp. 241-271.
- D. H. Zhang, D. A. Callaham and P. K. Hepler, “Regulation of Anaphase Chromosome Motion in Tradescantia Stamen Hair Cells by Calcium and Related Signalling Agents,” The Journal of Cell Biology, Vol. 111, No. 1, 1990, pp. 171-182. doi:10.1083/jcb.111.1.171
- E. D. Salmon and R. R. Segall, “Calcium-Labile Mitotic Spindles Isolated from Sea Urchin Eggs (Lytechinus variegatus),” The Journal of Cell Biology, Vol. 86, No. 2, 1980, pp. 355-365. doi:10.1083/jcb.86.2.355
- D. P. Kiehart, “Studies on the in Vivo Sensitivity of Spindle Microtubules to Calcium Ions and Evidence for a Vesicular Calcium-Sequestereing System,” The Journal of Cell Biology, Vol. 88, No. 3, 1981, pp. 604-617. doi:10.1083/jcb.88.3.604
- [61] W. Z. Cande, “Physiology of Chromosome Movement in Lysed Cell Models,” In: H. G. Schweiger, Ed., International Cell Biology, Springer Publishing Company, Berlin, 1981, pp. 382-391.
- [62] J. B. Olmsted and G. G. Borisy, “Ionic and Nucleotide Requirements for Microtubule Polymerization in Vitro,” Biochemistry, Vol. 14, No. 13, 1975, pp. 2996-3005. doi:10.1021/bi00684a032
- [63] R. B. Nicklas, “Chromosome Movement: Current Models and Experiments on Living Cells,” In: S. Inoue and R. E. Stephens, Eds., Molecules and Cell Movement, Raven Press, New York, 1975, pp. 97-117.
- [64] R. B. Nicklas, “Chromosomes and Kinetochores Do More in Mitosis than Previously Thought,” In: J. P. Gustafson, R. Appels and R. J. Kaufman, Eds., Chromosome Structure and Function, Plenum Publishing Company, New York, 1987, pp. 53-74.
- [65] E. D. Salmon, “Spindle Microtubules: Thermodynamics of in Vivo Assembly and Role in Chromosome Movement,” Annals of the New York Academy of Sciences, Vol. 253, 1975, pp. 383-406. doi:10.1111/j.1749-6632.1975.tb19216.x
- [66] E. D. Salmon, “Microtubule Dynamics and Chromosome Movement,” In: J. S. Hyams and B. R. Brinkley, Eds., Mitosis: Molecules and Mechanisms, Academic Press, San Diego, 1989, pp. 119-181.
- [67] S. L. Wolfe, “Molecular and Cellular Biology,” Wadsworth Publishing Company, Belmont, 1993, p. 425.
- [68] H. Diebler, G. Eigen, G. Ilgenfritz, G. Maass and R. Winkler, “Kinetics and Mechanism of Reactions of Main Group Metal Ions with Biological Carriers,” Pure and Applied Chemistry, Vol. 20, No. 1, 1969, pp. 93-116. doi:10.1351/pac196920010093

