Open Journal of Metal
Vol.04 No.03(2014), Article ID:49967,6 pages
10.4236/ojmetal.2014.43008
Construction of Solidus Lines of Binary Metal Systems Having a Low Solubility of Components in the Solid Phase
A. P. Shcherban, O. A. Datsenko, G. P. Kovtun
National Science Center, Kharkov Institute of Physics & Technology, Kharkov, Ukraine
Email: shcherban@kipt.kharkov.ua
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 July 2014; revised 13 August 2014; accepted 12 September 2014
ABSTRACT
The paper presents the calculation results on the construction of solidus lines of phase diagrams for some binary metal systems based on cadmium, zinc and tellurium. The investigations have been carried out using the phase equilibrium thermodynamics and known liquidus lines. By the calculation method the solidus lines of phase diagrams of the Cd-Na, Cd-Tl, Te-Ga, Te-As, Te-Cu and Zn-Sn systems were constructed in the temperature range from the base component melting point to the eutectic transformation temperature. In the Cd-Tl, Te-As, Te-Cu and Zn-Sn systems a retrograde solubility of the second component in the solid phase was observed. The temperature and maximum solubility values at the retrograde behavior of solidus lines, as well as, the limiting solubility values of components at eutectic transformation in the systems based on Cd, Zn and Te were determined.
Keywords:
Binary Metal System, Cadmium, Zinc, Tellurium, Phase Diagram, Solidus Line, Eutectic Transformation, Retrograde Solubility

1. Introduction
The investigation of the equilibrium phase transformation in the two-component metal systems is among the main problems of materials science. Although there are equilibrium deviations in any real system, the equilibrium phase diagrams serve as a basis for understanding of many phase transformation processes.
Whereas almost all the binary metal systems in the liquid phase possess a unlimited solubility, for many systems the mutual solubility of components in the solid phase is low (<1 at.%). Studying examples of phase diagrams (PD) of systems with a low solubility, being crystallized by the eutectic scheme, it should be noted that the complete mutual insolubility of components in the solid phase is a limiting case.
On the other hand, the base solid solutions with weakly soluble impurities are formed in the near temperature interval of crystallization. Therefore it is impossible to construct experimentally PD solidification curves (solidus lines). As an example we can mention such systems as two-component cadmium and zinc systems and binary tellurium systems [1] .
One of the ways for constructing solidus lines can be the calculation method taking into account thermodynamics of phase equilibriums and parameters of known PD liquidus lines. The thermodynamic approach with the use of a current computer-aided techniques permits to calculate PD unknown sections and thus to reduce significantly the scope of experiments on their construction [2] .
The aim of this study is to develop the calculation method for construction and analysis of PD solidus lines for binary metal systems with weakly soluble components in the solid phase.
2. Problem Definition
During formation of limited solid solutions the solubility maximum is reached, as a rule, at a temperature of three-phase equilibrium—eutectic (xSBE, Figure 1) or peritectic one. However, in some systems the solubility maximum of B component (xmaxB) corresponds to a higher temperature (systems with a retrograde solubility). A retrograde solubility phenomenon usually is observed in the systems with a weak solubility [3] .
One of parameters, being characteristic for the interphase equilibrium, is the equilibrium distribution coefficient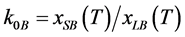 , where xSB and xLB are the B component concentrations in solid and liquid phases at corresponding temperatures respectively.
, where xSB and xLB are the B component concentrations in solid and liquid phases at corresponding temperatures respectively.
Proceeding from the suppositions, valid for ideal diluted solutions, in [4] the equation for the equilibrium distribution coefficient (DC) as a function of the B component concentration has been obtained in the following form
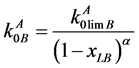 (1)
(1)
where the exponent α is determined by the formula
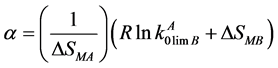 (2)
(2)
Here 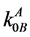 and
and 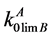 are the equilibrium and limiting distribution coefficients for the impurity B component in the base A component; xLB is the B component concentration in the liquid phase; R is the universal gas constant; ΔSMA, ΔSMB are the melting entropies of A and B components respectively.
are the equilibrium and limiting distribution coefficients for the impurity B component in the base A component; xLB is the B component concentration in the liquid phase; R is the universal gas constant; ΔSMA, ΔSMB are the melting entropies of A and B components respectively.
The exponent α for each pair of A-B components can take a positive, as well as, a negative value. In [4] [5] it is noted that the negative values of the exponent α, taking into account the melting entropies of two components,
Figure 1. Phase diagram with a retrograde solubility of B component (in diagram form).
suppose a probable occurrence of the retrograde solubility. At the same time Equation (2) for calculation of the exponent α, includes also the limiting DC of the B component which the determination of which is another problem. The limiting DC of impurities 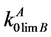 characterizes the impurity behavior near the temperature of base component melting. Before authors of this paper have proposed the calculation method of determining the limiting DC for the systems containing components being weakly soluble in the solid phase [6] . Also there are calculation values of limiting DC
characterizes the impurity behavior near the temperature of base component melting. Before authors of this paper have proposed the calculation method of determining the limiting DC for the systems containing components being weakly soluble in the solid phase [6] . Also there are calculation values of limiting DC 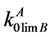 for some impurities in Cd, Zn and Te.
for some impurities in Cd, Zn and Te.
In connection with the previous calculations of parameters 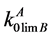 and α [7] , in the present paper we have chosen, as a subject of investigation, binary systems on the base of cadmium, zinc and tellurium. Besides, in [8] proposed was the calculation method for graphic representation of phase diagrams of two-component metal systems in the region of low component concentrations. Also there given are the plotted PD of cadmium, zinc and tellurium with some elements in the region of low impurity concentrations (from xSB < 0.1 at.% with extrapolation up to zero concentration).
and α [7] , in the present paper we have chosen, as a subject of investigation, binary systems on the base of cadmium, zinc and tellurium. Besides, in [8] proposed was the calculation method for graphic representation of phase diagrams of two-component metal systems in the region of low component concentrations. Also there given are the plotted PD of cadmium, zinc and tellurium with some elements in the region of low impurity concentrations (from xSB < 0.1 at.% with extrapolation up to zero concentration).
So, a problem of the present study was to construct, by the calculation method, the solidus lines in the region from the base component melting temperature to the eutectic transformation temperature and to reveal a possible retrograde solubility in the binary systems containing Cd, Zn and Te.
3. Calculation Method
The first stage of calculations for determining the initial values of solid solution concentrations near the base component melting temperature was to construct a liquidus line into the region of concentrations xLB ≤ 1 аt.%. The construction has been performed by the method of extrapolation of the equation for PD liquidus curve into the region of the impurity component zero concentration (the method is described in [6] [8] ).
To determine the values of solid solution concentrations in the concentration range from xLB ≥ 1 at.% to the eutectic we have used the liquidus line values xLB from the experimentally constructed PD [1] .
Using the expression of [9] [10] , the solidus line for the temperature dependence of the equilibrium DC was constructed with taking into account the thermodynamic parameters of two components
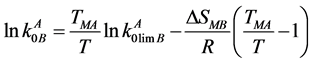 (3)
(3)
where 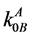 and
and 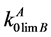 are the equilibrium and limiting coefficients of B component distribution in A component; R is the universal gas constant; ΔSMB is the B component melting entropy; ТМА is the base component melting temperature; T is the variable temperature of the liquidus line.
are the equilibrium and limiting coefficients of B component distribution in A component; R is the universal gas constant; ΔSMB is the B component melting entropy; ТМА is the base component melting temperature; T is the variable temperature of the liquidus line.
Using the determination of the equilibrium distribution coefficient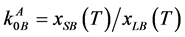 , Equation (3) can be described in the following form
, Equation (3) can be described in the following form
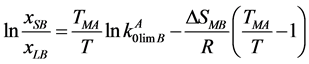 (4)
(4)
where xLB and xSB are the impurity element concentrations in the liquid and solid phases (in the liquidus and solidus lines);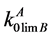 , R, ТМА and Т are the same parameters as in (3).
, R, ТМА and Т are the same parameters as in (3).
4. Results and Discussion
Table 1 gives the thermodynamic parameters used for the calculation of the second component concentration in the solid phase xSB(T) and for the subsequent construction of solidus lines of the systems under consideration.
To construct the solidus line the values xSB were obtained from Equation4 that has been solved using the mathematical packet Mathcad.
In Table 2 given are, as an example, the concentration values xLB at a variable temperature T and corresponding calculated concentrations xSB for the Zn-Sn and Cd-Tl systems, used for construction of PD solidus lines. Similar tables were also made for other systems studied below.
Figure 2 presents the assumed solidus lines constructed for the Cd-Na, Cd-Tl, Te-Ga, Te-As, Te-Cu, Zn-Sn systems according to the calculated values xSB.
As is seen from the plotted PD, in the Cd-Tl, Te-As, Te-Cu and Zn-Sn systems a retrograde character of the solidus line becomes apparent. A maximum solubility of Tl in Cd is 1.42 at.% at a temperature of 229.87
Table 1. Thermodynamic parameters for the computational construction of solidus lines for the Cd-Na, Cd-Tl, Te-Ga, Te-As, Te-Cu, Zn-Sn systems.
Table 2. Calculated values of solidus line concentration xs at a temperature T and calculated values of liquidus line concentration xl for the Zn-Sn and Cd-Tl systems.
degrees Celsius, As in Te—0.065 at.% at 384.34 degrees Celsius, Cu in Te—0.701 at.% at 229.87 degrees Celsius, Sn in Zn—1.82 at.% at 322.3 degrees Celsius. The results obtained are in agreement with the prediction on the possibility of retrograde solubility appearance, made by authors of [5] using the negative values of the exponent α in Equation (1).
The proposed method permits also to determine the limiting solubility of components in eutectic transformations (Figure 2). In Table 3 given are the maximum retrograde (xSBR) and eutectic (xSBE) solubility values and corresponding temperatures TR and TE for the binary systems containing cadmium, zinc and tellurium under study.
Figure 2. Calculated solidus lines (S) and liquidus lines (L) for the Cd-Na, Cd-Tl, Te-Ga, Te-As, Te-Cu, Zn-Sn systems.
Table 3. Maximum solubility concentrations and corresponding temperatures in the points of retrograde and eutectic transformations in the case of binary systems containing Cd, Te and Zn.
To verify the validity of Equation (4) application for the solidus line construction we have carried out calculations for PD with an experimentally determined explicit retrograde solubility in the region of significant solubility. It has been evidenced by the Co-Cu phase diagram demonstrating a distinct retrograde solubility [1] . The retrograde behavior of the Co solidus line was observed in [11] . A maximum solubility of Cu in Co is reached at a temperature of 1367 degrees Celsius and makes 19.7 at.% [11] . The solidus line, constructed by this method, coincides with the solidus line obtained by the generalized experimental data with a relative error of about 3.5% [1] . The calculated maximum solubility of Cu in Co equal to ≈ 19.7 at.% is reached at the same temperature T = 1367 degrees Celsius. A good agreement of calculated and experimental values is also observed for the limiting solubility in eutectic transformations.
For several systems based on Cd, Te and Zn with a low solubility of the second component we observed a retrograde solubility that confirms the assumptions made in [9] . According to [9] the retrograde solubility should be observed in the cases when the eutectic point is notably below the melting temperature and the solubility in the solid phase is low.
In our case the retrograde solubility has been observed in the system for which the eutectic temperature is by 100 degrees Celsius below the base component melting temperature and in the systems where this interval is less than 30 degrees Celsius it is not observed.
Analysis of results obtained shows a weak (~2% ··· 6%) retrograde solubility, as compared to the limiting solubility in eutectic transformations, for the Te-Cu, Te-As, Cd-Tl systems, and a higher (~43%) deviation of the retrograde solubility for the Zb-Sn system. Probably this is related with a high value of the partial enthalpy of tin dilution in zinc.
5. Conclusions
1) The calculation method for constructing the solidus lines of phase diagrams of binary metal systems having a low solubility in the solid phase has been proposed. By this method the phase diagrams were constructed for binary metal systems based on cadmium, zinc, tellurium in the range of the second component concentrations from 0.01 at.% to the eutectic line.
2) For the Te-Cu, Te-As and Cd-Tl systems a weak retrograde solubility of the second component in the solid phase (from 2% to 6% as compared to the limiting solubility in eutectic transformations) was found. In these systems the retrograde solubility temperature is by ~20 ··· 30 degrees Celsius higher than the eutectic transformation temperature. For the Zn-Sn system a higher deviation of the retrograde solubility (~43%), with the difference between retrograde and eutectic temperature near 124 degrees Celsius, was found.
3) For the first time the calculation method was applied to obtain the maximum solubility and temperature values with the retrograde behavior of liquidus lines, as well as, the limiting solubility values for the components undergoing eutectic transformations in the systems based on Cd, Zn and Te.
References
- Lyakishev, N.P. (1997) Phase Diagrams of Binary Metal System. Metallurgiya, Moscow, 1024 p.
- Kan, R.U. and Khaazen, P. (1987) Physical Metallurgy. Metallurgiya, Moscow, 624 p.
- Svellin, R.A. (1968) Solid Phase Thermodynamics. Metallurgiya, Moscow, 316 p.
- Romanenko, V.N. (1960) The Influence of the Concentration Dependence of the Segregation Coefficient on the Redistribution of the Components in a Binary System during Oriented Crystallization. Solid Phase Physics, 2, 866-869.
- Barthel, J., Buhrig, E., Hein, K. and Kuchar, L. (1987) Cristallisation aus Schmelzen. Reference Manual: Translation from German. Metallurgiya, Moscow, 320 p.
- Kovtun, G.P., Scherban, A.P. and Datsenko, O.A. (2003) Calculation Method for Determining the Limiting Impurity Distribution Coefficients k0limB at the Directional Crystallization of Metals. In: Voprosy atomnoj nauki i tekhniki. No 5. Series: Vacuum, Pure Materials, Superconductors, Volume 13, 3-6.
- Scherban, A.P. and Kovtun, G.P. (2014) Estimation of the Solubility Limit of Low-Soluble Components under Eutectic Transformations in the Binary Metal Systems. Problem of Atomic Science and Engineering, 89, 37-40
- Scherban, A.P. and Datsenko O.A. (2013) Analysis of Phase Diagrams of Binary Metal Systems in the Field at Low Concentration of Components. Journal of V. N. Karazin Kharkiv National University, 60, 95-99.
- Kröger, F.A. (1969) Chemistry of Imperfect Crystals. North-Holland, Amsterdam, 654 p.
- Hall, R.N. (1957) Variation of the Distribution Coefficient and Solid Solubility with Temperature. Journal of Physics and Chemistry of Solids, 3, 63-73. http://dx.doi.org/10.1016/0022-3697(57)90049-5
- Hasebe, M. and Nishizawa, T. (1980) Calculation of Phase Diagrams of the Iron-Copper and Cobalt-Copper Systems. Calphad, 4, 83-100. http://dx.doi.org/10.1016/0364-5916(80)90026-7




