Journal of Power and Energy Engineering
Vol.07 No.07(2019), Article ID:93966,10 pages
10.4236/jpee.2019.77003
Numerical Analysis of an Industrial Polycrystalline Silicon Photovoltaic Module Based on the Single-Diode Model Using Lambert W Function
Mihai Răzvan Mitroi1, Valerică Ninulescu1, Laurenţiu Fara1,2*, Dan Crăciunescu1
1University Politehnica of Bucharest, Bucharest, Romania
2Academy of Romanian Scientists, Bucharest, Romania

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 26, 2019; Accepted: July 26, 2019; Published: July 29, 2019
ABSTRACT
It is adopted the single-diode solar cell model and extended for a PV module. The current vs. voltage (I-V) characteristic based on the Lambert W-function was used. The estimation parameters for the simulation approach of the photovoltaic (PV) module make use of Levenberg-Marquardt method. It was considered an industrial polycrystalline silicon photovoltaic (PV) module and the simulated results were compared with the experimental ones extracted from a specific datasheet. The I-V characteristic for the analysed PV module and its maximum output power are investigated for different operating conditions of incident solar radiation flux and temperature, as well as parameters related to the solar cells material and technology (series resistance, shunt resistance and gamma factor). The analysis gives indications and limitations for design and optimization of the performance for industrial PV modules. This study can be implemented in any type of PV module.
Keywords:
Single-Diode Model, Electrical Modeling, I-V Characteristic, Numerical Analysis, Industrial PV Module Performance

1. Introduction
Recently, circuit-based models of photovoltaic (PV) arrays are being developed in order to predict the performance of PV modules in different operating conditions like solar irradiance and temperature. The modeling is performed via current vs voltage characteristic and this is a highly constrained nonlinear optimization problem.
There are many methods presented in the literature for modeling PV modules. Among these, the single-diode model and the two-diode model are widely adopted [1] [2] . A comprehensive review of all modeling techniques is also available [3] [4] [5] [6] . Most of the models are focused on monocrystalline and polycrystalline PV modules using different techniques. For instance, the single-diode model proposed by Gradella [7] presents a power matching algorithm by varying the series and shunt resistances simultaneously, for accurately fitting the characteristic curve at standard testing conditions. The diode ideality factor is arbitrarily chosen. This concept is extended to two-diode model [8] . There are many other models presented in the literature that use conventional methods based on datasheet parameters [9] [10] [11] . All these models accurately predict the I-V characteristics for monocrystalline and polycrystalline modules, whereas they fail in a fair prediction of the characteristics of thin film solar cells. Other methods presented in literature are based on optimization and soft computing techniques. Even though these methods envisage the behavior of PV modules accurately, they are highly complex. A modeling approach for PV modules based on amorphous silicon solar cells [12] considers an improved single diode model with two additional parameters.
Three types of PV modules are mostly commercialized: monocrystalline silicon modules, polycrystalline silicon modules and thin film modules. The performance among the three types varies in a decreasing order, from former to latter [7] .
2. Modeling Approach to the PV Module
2.1. Electrical Modeling
The electrical equivalent of a single-diode PV cell is presented in Figure 1, where: IL is the light-generated current in the absorber layer, Id—current through the diode, I—the total current, and V—the output voltage, Rs—the series resistance, Rsh—the shunt resistance.
Under illumination, the total current I [13] written for a PV module consisting of Ns cells connected in series is
(1)
Figure 1. Single-diode model of a PV cell that includes a series and a shunt resistance.
where: I0 is the reverse saturation current corresponding to the diode, Vth = kBT/q is the thermal voltage, kB and q are the Boltzmann constant and the elementary charge, respectively, γ is the diode ideality factor and T is module temperature. The value of γ is 1 for an ideal diode and greater than 1 for a real one, depending on the type of defects or/and recombination mechanisms. The series resistance takes into account the losses in neutral zones, in cell solder bonds, interconnection, junction box, etc., that are cell manufacturing dependent; the shunt resistance is due to the generation-recombination processes in the space charge region of the cell and to the leakage currents at the surface, i.e. it depends on the composition of the absorber layer [14] [15] .
The light-generated current in the absorber layer is
(2)
where Ginj is the photoelectron generation rate and L is the thickness of the absorber layer. The photoelectron generation rate is directly proportional to the incident light flux power density [16] and should take into account the carrier-injection efficiency. The absorber layer is responsible for absorption and conversion of incident photons into charge carriers.
By use of Lambert W function [17] , Equation (1) becomes
(3)
where βPV is the PV module parameter that characterizes the efficiency due to the light reflection and absorption in the transparent glass layer of the PV module, which depends on its materials and design.
The solution based on Lambert W function is exact and explicit. One can see that I depends on six parameters: Is, Rs, Rsh, T, γ and βPV.
The short-circuit current Isc, is obtained substituting V = 0 in Equation (3)
(4)
and the open-circuit voltage Voc is obtained, substituting I = 0 in Equation (3):
(5)
2.2. The Influence of Temperature
The PV modules are generally used at temperatures ranging from −15˚C ÷ 50˚C and to even higher temperatures in space applications and concentrator systems. Many studies have pointed out that the performance of solar cells degrades as temperature increases. The variation of Rs and Rsh with temperature affects slightly the efficiency [18] [19] . In this paper, we analyze the variation of parameters Vth and I0 with temperature. The thermal voltage dependence on temperature is
(6)
where is the thermal voltage at the standard temperature T = 298 K.
The reverse-bias saturation current depends on temperature according to Attivissimo [20] :
(7)
where Eg is the bandgap energy of the absorber layer. and Eg depends on temperature by the relationship:
(8)
where Eg(0) is the band gap value at T ≈ 0 K, and a and b are constants. The values of the parameters in Equation (8) are Eg(0) = 1.166 eV, a = 4.73 × 10−4 eV/K and b = 636 K [21] .
3. Numerical Analysis of an Industrial PV Module
An industrial PV module was analyzed based on the theoretical model discussed above. We analyzed a PV module produced by Tritech Group PV manufacturer [22] , WT 60P-SM_255W, consisting of Ns = 60 polycrystalline silicon cells grouped in series. The performance of a PV module is analyzed by numerical simulation for AM 1.5 G solar spectrum and standard temperature conditions [23] .
The model parameters I0, Rs, Rsh, βPV and γ as function of the incident light flux power density were determined by fitting Equation (3) with datasheet data for the PV module. The fitting program is based on the Levenberg-Marquardt method. The results are listed in Table 1. A dedicated software solves Equation (4) and Equation (5), and computes the PV module parameters Isc, Voc, FF, PM and η. These values are presented in Table 2 and compared with the datasheet ones (http://wattrom.com). The relative error in the calculated parameters is also highlighted.
The I-V curve with model parameters of Table 1 is traced in Figure 2 and compared with that from the datasheet. The correlation coefficient is greater than 0.99.
Table 1. Model parameters obtained by fitting Equation (1) with the I-V curve from the datasheet.
Table 2. PV module parameters obtained for the values from Table 1.
Figure 2. I-V characteristic of the PV module for 2 cases: Tritech Group datasheet (о) and fitted (−).
3.1. Influence of Solar Irradiance
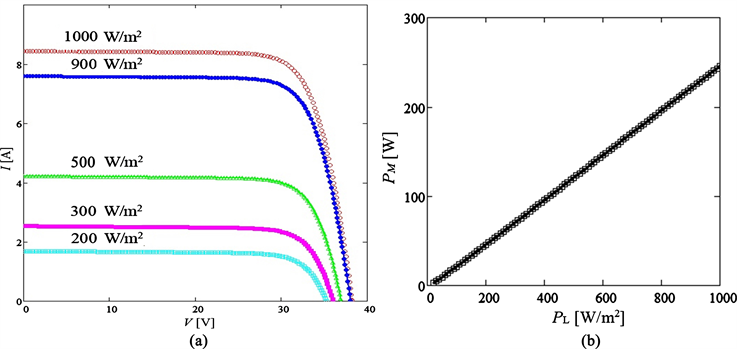
The impact of the some power densities of the incident light flux of solar irradiance (PL) on the current vs voltage characteristic is shown in Figure 3(a), thus resulting in a maximum output power that decreases linearly (Figure 3(b)). This change is mainly attributed to the lowering of the current at the maximum power point. The comparison for the voltage and current at the maximum power point relative to that at the standard conditions (1000 W/m2) with datasheet values is presented in Table 3.
3.2. Influence of the Parameters Rs, Rsh and γ
We analyzed the influence of the parameters Rs, Rsh and γ on the current-voltage characteristic and on the maximum output power for the PV module. Each parameter was varied within a range in good agreement with other studies [10]
Figure 3. Influence of incident light flux power density on the solar PV module: I-V characteristic (a) and maximum output power (b).
Table 3. The voltage and current at the maximum power point relative to that at the standard conditions for some power densities of the incident light flux.
[11] [24] [25] . We considered the standard conditions and βPV = 0.9 for all simulations. The parameter values that are kept constant in each case are from Table 2. Figure 4 shows the influence of the series resistance (a), the shunt resistance (b) and the ideality factor (c) on the I-V curve and maximum output power (PM). The increase of Rsh and γ improves the performance of the PV module, while the increase of Rs contributes to a performance decrease. The increase due to the ideality factor is significant within the range 1 < γ < 2.
3.3. Influence of Temperature
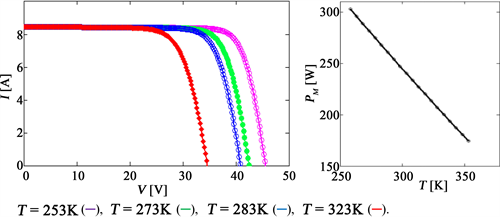
The temperature influence on the I-V characteristic and output power was analyzed using Equations (7) and (8). Figure 5 shows this dependence. A strong output power decrease with increasing the temperature is observed.
The decrease of maximum output power is of 19.48% for a temperature increase of 30 K, from T* = 298 K to T = 328 K. This aspect is mainly due to the temperature dependence of the current I0 [Equation (7)] that undergoes a rapid increase with temperature. The results indicate that the temperature is a major factor in decreasing the PV module performance [26] , which has to be considered in module design.
Figure 4. Influence of series resistance (a), shunt resistance (b) and ideality factor (c) on the PV module I-V characteristic and maximum output power.
Figure 5. Influence of the temperature on the I-V characteristic and maximum output power of the PV module.
4. Conclusions
This study presents a comprehensive numerical analysis of performance optimization of a PV module based on polycrystalline silicon solar cells grouped in series.
The novelty of this research consists in the numerical analysis based on single diode model applied for a PV module and the use of the Lambert W function for such an approach.
The numerical analyses were considered in-depth from two points of view:
1) There were compared the simulated results with the experimental ones based on the datasheet values regarding the main performance parameters for an industrial PV module namely: Isc, Voc, PM, FF, η.
2) It was considered the influence of temperature and solar irradiance (incident light flux power density) on I-V characteristics and maximum output power of the analysed PV modules.
The analytical expression of the current I is directly used to fit the experimental values and extract the model parameters: I0, Rs, Rsh, γ and βPV using the Levenberg-Marquardt estimation method. These describe the technological characteristics of the PV module. The performance parameters of PV module Isc, Voc, FF and η are in good agreement with the data for industrial PV module.
The influence of the parameters PL, Rs, Rsh, γ and T on the maximum output power of the PV module is emphasized. The obtained results are consistent with those reported in literature [10] [11] [24] [25] . The numerical analysis performed in this work provides indications for design and optimization of the PV modules performance.
The limitations of the analysed research method are determined by the constraints of Rs, Rsh and γ technological parameters on the industrial PV module performances.
This model and the corresponding numerical analysis can be implemented to any type of PV module, such as those based on silicon and metal oxide tandem solar cells.
Acknowledgements
This research was conducted under the research project “High-performance tandem heterojunction solar cells for specific applications (SOLHET)”, funded by the Research Council of Norway (RCN), project no. 251789, and the Romanian Executive Agency for Higher Education, Research, Development and Innovation Funding (UEFISCDI), project no. 34/2016 and 35/2016, through the M-Era.net program.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Mitroi, M.R., Ninulescu, V., Fara, L. and Crăciunescu, D. (2019) Numerical Analysis of an Industrial Polycrystalline Silicon Photovoltaic Module Based on the Single-Diode Model Using Lambert W Function. Journal of Power and Energy Engineering, 7, 29-38. https://doi.org/10.4236/jpee.2019.77003
References
- 1. Hejri, M., Mokhtari, H., Azizian, M.R., Ghandhari, M. and Soder, L. (2014) On the Parameter Extraction of a Five-Parameter Double-Diode Model of Photovoltaic Cells and Modules. IEEE Journal of Photovoltaics, 4, 915-923. https://doi.org/10.1109/JPHOTOV.2014.2307161
- 2. Tolic, I., Primorac, M. and Milicevic, K. (2019) Measurement Uncertainty Propagation through Basic Photovoltaic Cell Models. Energies, 12, 1029. https://doi.org/10.3390/en12061029
- 3. Abbassi, R., Abbassi, A., Jemli, M. and Chebbi, S. (2018) Identification of Unknown Parameters of Solar Cell Models: A Comprehensive Overview of Available Approaches. Renewable and Sustainable Energy Reviews, 90, 453-474. https://doi.org/10.1016/j.rser.2018.03.011
- 4. Jena, D. and Ramana, V.V. (2015) Modeling of Photovoltaic System for Uniform and Non-Uniform Irradiance: A Critical Review. Renewable and Sustainable Energy Reviews, 52, 400-417. https://doi.org/10.1016/j.rser.2015.07.079
- 5. Aernouts, T. (2006) Organic Bulk Heterojunction Solar Cells: From Single Cell towards Fully Flexible Photovoltaic Module. PhD Thesis, Departement Natuurkunde, Faculteit Wetenschappen, Katholieke Universiteit Leuven, Belgium. https://core.ac.uk/download/pdf/34435199.pdf
- 6. Lineykin, S., Averbukh, M. and Kuperman, A. (2012) Five-Parameter Model of Photovoltaic Cell Based on STC Data and Dimensionless. 27th Convention of Electrical and Electronics Engineers in Israel, Eilat, 14-17 November 2012, 13173063. https://doi.org/10.1109/EEEI.2012.6377079
- 7. Gradella, V.M., Gazoli, J.R. and Filho, E.R. (2009) Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Transactions on Power Electronics, 24, 1198-1208. https://doi.org/10.1109/TPEL.2009.2013862
- 8. Kashif, I., Salam, Z. and Taheri, H. (2011) Simple, Fast and Accurate Two-Diode Model for Photovoltaic Modules. Solar Energy Materials and Solar Cells, 95, 586-594. https://doi.org/10.1016/j.solmat.2010.09.023
- 9. Herbazi, R., Amechnoue, K., Khouya, A. and Louzazni, M. (2019) Investigation of Photovoltaic Output Characteristics with Iterative Methods. Procedia Manufacturing, 32, 794-801. https://doi.org/10.1016/j.promfg.2019.02.287
- 10. Kumar, S., Sahu, H.S. and Nayak, S.K. (2019) Estimation of MPP of a Double Diode Model PV Module from Explicit I-V Characteristic. IEEE Transactions on Industrial Electronics, 66, 7032-7042. https://doi.org/10.1109/TIE.2018.2877116
- 11. Ramana, V.V., Jena, D. and Gaonkar, D.N. (2016) An Accurate Modeling of Different Types of Photovoltaic Modules Using Experimental Data. International Journal of Renewable Energy Research, 6, 970-974.
- 12. Simon, L., Averbukh, M. and Kuperman, A. (2014) Issues in Modeling Amorphous Silicon Photovoltaic Modules by Single-Diode Equivalent Circuit. IEEE Transactions on Industrial Electronics, 61, 6785-6793. https://doi.org/10.1109/TIE.2014.2317138
- 13. Ishibashi, K., Kimura, Y. and Niwano, M. (2008) An Extensively Valid and Stable Method for Derivation of All Parameters of a Solar Cell from a Single Current-Voltage Characteristic. Journal of Applied Physics, 103, Article ID: 094507. https://doi.org/10.1063/1.2895396
- 14. van Dyk, E.E. and Meyer, E.L. (2004) Analysis of the Effect of Parasitic Resistances on the Performance of Photovoltaic Modules. Renewable Energy, 29, 333-344. https://doi.org/10.1016/S0960-1481(03)00250-7
- 15. Ghani, F. and Duke, M. (2011) Numerical Determination of Parasitic Resistances of a Solar Cell Using the Lambert W-Function. Solar Energy, 85, 2386-2394. https://doi.org/10.1016/j.solener.2011.07.001
- 16. Mitroi, M.R., Ninulescu, V. and Fara, L. (2017) Tandem Solar Cells Based on Cu2O and c-Si Sub-Cells in Parallel Configuration: Numerical Simulation. International Journal of Photoenergy, 2017, Article ID: 7284367. https://doi.org/10.1155/2017/7284367
- 17. Jain, A. and Kapoor, A. (2004) Exact Analytical Solutions of the Parameters of Real Solar Cells Using Lambert W-Function. Solar Energy and Materials, 81, 269-277. https://doi.org/10.1016/j.solmat.2003.11.018
- 18. Abderrezek, M., Fathi, M., Mekhilef, S. and Djahli, F. (2015) Effect of Temperature on the GaInP/GaAs Tandem Solar Cell Performances. International Journal of Renewable and Sustainable Energy, 5, 629-634.
- 19. Singh, P. and Ravindra, N.M. (2012) Temperature Dependence of Solar Cell Performance—An Analysis. Solar Energy Material and Solar Cells, 101, 36-45. https://doi.org/10.1016/j.solmat.2012.02.019
- 20. Attivissimo, F., Di Nisio, A., Savino, M. and Spadavecchia, M. (2012) Uncertainty Analysis in Photovoltaic Cell Parameter Estimation. IEEE Transactions on Instrumentation and Measurement, 61, 1334-1342. https://doi.org/10.1109/TIM.2012.2183429
- 21. Van Zeghbroeck, B. (2004) Principles of Semiconductor Devices.
- 22. Tritech Group. http://wattrom.com
- 23. Yang, J., Sun, Y. and Xu, Y. (2013) Modeling Impact of Environmental Factors on Photovoltaic Array Performance. International Journal of Energy and Environment, 4, 955-968.
- 24. Calnan, S. (2014) Applications of Oxide Coatings in Photovoltaic Devices. Coatings, 4, 162-202. https://doi.org/10.3390/coatings4010162
- 25. ASTM G173-03 Reference Spectra Derived from SMARTS v. 2.9.2. https://rredc.nrel.gov/solar//spectra/am1.5/ASTMG173/ASTMG173.html
- 26. Varshni, Y.P. (1967) Temperature Dependence of the Energy Gap in Semiconductors. Physica, 34, 149-154. https://doi.org/10.1016/0031-8914(67)90062-6