Journal of Power and Energy Engineering
Vol.04 No.06(2016), Article ID:67898,14 pages
10.4236/jpee.2016.46003
Design Optimization of a Micro-Combustor for Lean, Premixed Fuel-Air Mixtures
Leigh T. Powell, Ralph C. Aldredge
Department of Mechanical and Aerospace Engineering, University of California-Davis, Davis, CA, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 June 2016; accepted 27 June 2016; published 30 June 2016
ABSTRACT
Present technology has been shifting towards miniaturization of devices for energy production for portable electronics. Micro-combustors, when incorporated into a micro-power generation system, create the energy desired in the form of hot gases to power such technology. This creates the need for a design optimization of the micro-combustor in terms of geometry, fuel choice, and material selection. A total of five micro-combustor geometries, three fuels, and three materials were com- putationally simulated in different configurations in order to determine the optimal micro-com- bustor design for highest efficiency. Inlet velocity, equivalence ratio, and wall heat transfer coefficient were varied in order to test a comprehensive range of micro-combustor parameters. All simulations completed for the optimization study used ANSYS Fluent v16.1 and post-processing of the data was done in CFD Post v16.1. It was found that for lean, premixed fuel-air mixtures (φ = 0.6 - 0.9) ethane (C2H6) provided the highest flame temperatures when ignited within the micro- combustor geometries. An aluminum oxide converging micro-combustor burning ethane and air at an equivalence ratio of 0.9, an inlet velocity of 0.5 m/s, and heat transfer coefficient of 5 W/m2-K was found to produce the highest combustor efficiency, making it the optimal choice for a micro- combustor design. It is proposed that this geometry be experimentally and computationally investigated further in order to determine if additional optimization can be achieved.
Keywords:
Micro-Combustor, Combustion, Computational Fluid Dynamics, Ethane, Efficiency

1. Introduction
Present technology has been shifting towards miniaturization of devices for energy production in order to be useful to the everyday person. This miniaturization has created the need for micro-combustion, the exothermic chemical reaction between a fuel and oxidizer yielding the production of heat at the micro level. Portable communication devices, personal computers, and even portable media players all depend on some sort of energy production, usually in the form of a battery. The inevitable bulk associated with conventional batteries has become cumbersome and a growing need for a smaller and lighter power supply has emerged [1] . The invention of the micro-combustor has become one of the answers to this design problem. Such devices also have the capability to increase the amount of time one is able to use an electronic device normally powered by a battery. Micro- combustors can be part of a system replacing a typical lithium-ion battery or used in a more complex system such as a micro-engine or micro gas turbine generator. As early as 1997 the Massachusetts Institute of Technology (MIT) Gas Turbine Laboratory produced a study on fabrication of a micro gas turbine generator, which has been credited as being the impetus for the design of microelectromechanical systems (MEMS) devices [1] . This type of technology nevertheless comes with its share of challenges regarding fluid dynamics, combustion, and heat transfer. Viscous forces, reaction times, and surface-to-volume ratio are just some of the considerations that need to be addressed in micro-combustor design. A fair amount of research has been conducted on the operating conditions and ability of micro-combustors to stabilize flames [2] - [5] . A variety of fuels, geometries, and materials have been tested experimentally and computationally, however a comprehensive design optimization for the micro-combustor has featured very little in previous literature. This paper focuses on determining the best design option for a micro-combustor: the best fuel to use, the best geometry, and the best material from which to construct the micro-combustor.
2. Background
2.1. Micro-Combustors
Micro-combustors are miniaturized versions of macro scale combustors and are similar in function. The scale of such devices is separated into two groups: the microscale and the mesoscale. The microscale includes micro- combustor diameters up to 1 millimeter, while the mesoscale accounts for any other devices with a diameter larger than that. Several micro-combustor geometries have been tested and simulated in previous studies, including constant-diameter, backward-facing step, Swiss roll, and annular configurations [1] . While macro scale combustors used in conventional combustion systems are large enough to accommodate mixing of fuel and oxidizer within the combustion chamber, micro-combustors, on the other hand, are not afforded this convenience. Micro-combustors are usually operated with premixed fuel and oxidizer for combustion due to the limited space with which to allow mixing. The fuel-oxidizer mixture enters through the inlet of the micro-combustor and is ignited at a high temperature, causing the reactants to combust and form a flame. A burst of energy in the form of high temperature gases is produced and can be harnessed by a micro-turbine in a mechanical system in order to generate power for use in the previously mentioned electronic devices. There have been several advantages of micro-combustors presented in previous literature, almost all of which are due to the use of hydrocarbons as fuel for combustion. When used as a replacement to lithium-ion batteries, two notable advantages are the high energy density output and longer operational time of a micro-combustor. The large density of energy production is attributed to the use of hydrocarbon fuels for combustion in these devices: the energy density produced by these types of fuels is several orders of magnitude greater than that of a typical battery. Also of note is the advantage micro-combustors have in regards to environmental impact and overall size. When hydrocarbons have been properly combusted, primarily water and carbon dioxide result as products, whereas batteries contain several toxic chemicals and heavy metals that can pollute the environment when not disposed of properly. In addition, micro-combustors have become increasingly appealing as an alternative for energy production in portable electronics due to their small size and weight. One of the main disadvantages of micro-combustors is the surface- to-volume ratio, which can cause thermal quenching by way of excessive heat loss to the surrounding environment. For conventional combustors heat loss across the combustor walls can be neglected, however in micro- combustors the heat loss is more significant. Other disadvantages include flame instability in smaller and larger diameter micro-combustors and short residence times for mixing and combustion. Residence time is the amount of time that the gases are present within the micro-combustor: larger residence times allow for more complete combustion of the mixture. Because micro-combustors are so small, the residence time is greatly reduced and complicates the combustion process. Complete combustion is desired in all applications in order to lower emissions and produce as much usable energy as possible. Micro-combustors have a number of applications for use in present and future technology. They can be used in mechanical systems, such as micro-turbines and micro- rockets, or can be used in micro-thermophotovoltaic (TPV) systems that can take the place of an everyday battery. TPV systems convert the thermal energy production from combustion in a micro-combustor into electrical energy through the use of a thermal emitter and photovoltaic cells. MEMS (microelectromechanical systems) devices, in which micro-combustors are chief components, are being developed in order to match their large- scale counterparts in thermal, electrical, and mechanical power densities [6] . Such mechanisms have the potential to achieve similar performance but at a much smaller physical scale. Micro-combustors also have applications in micro-propulsion where they have been used to generate thrust and provide control for small satellites [7] .
2.2. Model Validation
In order to validate the solver preferences, boundary conditions, and other variables that were to be used in si- mulations for this study, the work of Murali [8] detailing premixed methane-air combustion in a micro-com- bustor was chosen as a template. One of the predominate reasons that this paper was chosen for validation purposes is that the authors also used Fluent for their CFD simulations and because of the basic geometry. The simulation is simple: the premixed methane-air mixture, at an equivalence ratio (φ) of 0.6, enters the inlet of a constant-diameter micro-combustor at 300 K and is ignited by a patched temperature of 1600 K over the entire domain. The simulation is steady-state and a schematic of the domain can be seen in Figure 1, where d represents the diameter of the micro-combustor. The micro-combustor has a wall thickness of 0.2 mm. The simulation is two-dimensional and uses a 5-step global chemical reaction mechanism used specifically for lean, premixed methane-air combustion. Stainless steel with a thermal conductivity of 20 W/m-K, a heat transfer coefficient of 50 W/m2-K, and emissivity of 0.2 was specified as the micro-combustor material for these validation simulations. For this validation case, half of the geometry was used by imposing a symmetry plane along the longitudinal axis. This cuts down on the mesh cell count, which in turn speeds up the simulation run time. As stated above, the simulation is steady-state; the pressure-based solver and an absolute velocity formulation were chosen, as well as specifying that the simulation be axisymmetric in 2D space. Gravity was not considered in these simulations. The energy equation was used as well as the realizable k-ε turbulence model; for the species transport the finite-rate/eddy-dissipation turbulence-chemistry interaction was used for the volumetric reactions. The inlet was set to a velocity-inlet boundary condition, with species mass fractions of methane (CH4) and oxygen (O2) set to 0.034 and 0.225, respectively. The outlet was set to a pressure-outlet boundary condition, with gauge pressure equal to 0 and species mass fractions of oxygen (O2), carbon dioxide (CO2), and water (H2O) set to 0.05, 0.1, and 0.1, respectively. The species mass fractions at the outlet are used in backflow calculations if cells near the outlet have lower pressure than the prescribed pressure of the outlet. At the walls a mixed boundary condition is used, which combines external radiation and convection heat transfer. A cold flow was first solved for by running a non-reacting simulation for 300 iterations first. Once the cold flow simulation was completed, the domain was patched in order to simulate ignition of the mixture inside the micro-combustor. The pressure-velocity coupling scheme was chosen to be SIMPLE. Pressure spatial discretization was seconder order; all gradients were computed using the least squares cell-based scheme. The second-order upwind scheme was used to solve for momentum, turbulent kinetic energy, turbulent dissipation rate, all species, and energy.
The reacting flow was solved for by reaching a convergence of 1e−06 for the residuals. Most of these default parameters were described in the reference work of Murali [8] ; for the parameters not explicitly stated, such as outlet species mass fractions, realistic values were chosen in order to obtain matching results. The simulation was run in Fluent for four velocities: u = 0.3 m/s, 0.5 m/s, 0.8 m/s, and 1.0 m/s. The solution converged in several thousand iterations. The profiles of temperature, velocity, and methane mass fraction for each inlet velocity can be seen in Figure 2.
It can be seen from the results that as the inlet velocity is increased, higher maximum temperatures inside the micro-combustor are reached, and the flame tends to shift more towards the outlet. In the region where the
Figure 1. Schematic of 1 mm × 10 mm micro-combustor.
Figure 2. Profiles of temperature, velocity, and CH4 mass fraction for (a) u = 0.3 m/s; (b) u = 0.5 m/s; (c) u = 0.8 m/s; and (d) u = 1.0 m/s.
maximum temperatures are located the flow becomes faster along the centerline of the geometry. The mass fraction profiles show the reaction region moving further downstream as inlet velocity is increased as well as complete combustion of the methane. Also, in terms of the flame’s shape, at higher velocities the flame becomes more pointed rather than rounded at lower velocities. All maximum temperatures calculated in ANSYS Fluent v16.1 were within 4% of the temperatures reported in the reference work of Murali [8] . Flame shapes simulated were also qualitatively close to those seen in the reference work, however flame positions in the micro-com- bustor were slightly off. The flame positions simulated were somewhat closer to the inlet than those reported by Murali [8] . The velocity and methane mass fraction profiles are also comparable to those reported in the paper. These results justify the solver settings and parameters chosen to successfully model the methane-air combustion in a micro-combustor.
3. Design Parameters Simulated
3.1. Geometry
Five micro-combustor geometries were considered for these simulations: a constant-diameter, diverging, converging, converging-diverging, and backward-facing step geometry. These geometries were chosen due to previous experiments and computational simulations focusing on micro-combustor performance. The most common geometry used for micro-combustor research is the constant-diameter micro-combustor. This geometry is very simple and is both easily manufactured for experiments and modeled for computational simulations. It has been shown that flames can easily stabilize inside this type of geometry, which is of particular interest in micro-combustor research. A diverging geometry was used in these micro-combustor simulations due to its ability to slow down the flow within it. It was thought that because of the decrease in the speed of the flow that the flame would be anchored closer to the channel inlet for higher velocities and thus more stable. The converging micro-combustor geometry was chosen for these simulations due to its ability to speed up the flow at the exit plane. A converging-diverging geometry was used in these simulations after review of the work of Yang et al. [9] , in which the geometry was used in an experiment focusing on flame characteristics. It was seen in this investigation that higher velocities create higher temperature flows within the micro-combustor which in turn can cause an increase in efficiency. Lastly, the backward-facing step geometry is also simulated. Although it is less common than the constant-diameter micro-combustor, this particular geometry has also been used quite a bit in experimental and computational simulations. The backward-facing step near the inlet of the micro-combustor helps to anchor and stabilize the flame.
3.2. Fuels
The selection of a fuel for combustion is very important. The fuel needs to have a high enough heat of combustion to produce the required energy output. Hydrocarbons as well as hydrogen are the most common fuels used in micro-combustion due to their cost, availability, and high volume to energy density ratio. The diatomic form of hydrogen (H2) is extremely combustible with air as an oxidizer at a wide range of concentrations (4% - 75% by volume). Hydrogen has one of the highest heats of combustion at about 140 MJ/kg and has a lower ignition energy compared to most hydrocarbons, making it a go-to fuel for any combustion application. Hydrocarbons, such as methane (CH4) and hexane (C6H14), are the main fuels used in combustion presently because of the energy (in the form of heat) produced in the reactions. Methane (CH4) has an adiabatic flame temperature of 2226 K and a heat of combustion (production of heat per mass unit) of 55.528 MJ/kg, which is the highest for any hydrocarbon fuel and makes it an ideal candidate for micro-combustion [6] . Ethane (C2H6), normally found in its gaseous state, has an adiabatic flame temperature for stoichiometric combustion with air of 2259 K. The heat of combustion for ethane is 51.901 MJ/kg, just slightly lower than that of methane, making it another excellent fuel choice for micro-combustion [10] .
3.3. Materials
Material selection is important in micro-combustor design and performance. Not only must the material be able to withstand the high temperature flow caused by the combustion process, it must also protect against heat loss to the ambient surroundings. Three materials were chosen to be tested in these simulations: stainless steel, aluminum oxide, and crystal quartz. Several earlier researchers have used stainless steel as their material of choice when testing micro-combustors [8] [11] [12] . This material is low maintenance, easy to manufacture, and quite abundant. Stainless steel does not easily corrode, making it one of the ideal materials for a micro-combustor. Aluminum oxide (Al2O3), or alumina as it’s commonly referred to, is a compound comprised of aluminum and oxygen and comes in many forms, including as a ceramic. In this state it has been used as an insulator in electrical applications as well as for thermal processes. Due to its moderate thermal conductivity and ability to resist corrosion, this oxide ceramic was tested as a possible micro-combustor material. Although crystal quartz has mainly been used in jewelry making, a few papers were found to use quartz as their material of choice for micro- combustor experiments. This material, like stainless steel, is readily available and it also has a low thermal conductivity.
4. Results and Discussion
In order to determine what the best micro-combustor design is a variety of simulations were conducted using ANSYS Fluent v16.1 and analyzed using ANSYS CFD Post v16.1. The simulations were split up by the various design parameters studied: geometry, fuel, and material. Each of the five geometries was tested at an equivalence ratio of 0.6 and velocities of 1.0 and 0.5 m/s. The effect of changing the equivalence ratio for each fuel was tested with the 1 mm × 10 mm constant-diameter micro-combustor; lean equivalence ratios of 0.6, 0.7, 0.8, and 0.9 were used in these instances. Each of the three previously mentioned materials was tested for the micro- combustor with the 1 mm × 10 mm geometry for each fuel and with a range of heat transfer coefficients. The following simulations all have a fuel-air mixture entering the micro-combustor at the inlet at a temperature of 300 K with a prescribed uniform velocity. The mixture is ignited at 1,600 K, the pressure is set at atmospheric (101,325 Pa), and the ambient temperature of the surroundings is 300 K. These simulations are 2D axisymmetric with only half the geometry meshed and simulated. Residuals have converged to 1e−06 for all solutions. The results and discussion provided in this section all center on maximum temperatures calculated in the micro-com- bustor simulations due to the fact that micro-combustor efficiency and exit temperature are directly related: the higher the maximum temperature seen in the micro-combustor, the higher the exit temperature and consequently the efficiency will be. In addition, flame shape and stability are also commented on.
4.1. Geometry Performance
In order to determine which geometry is best for a micro-combustor design, the five previously mentioned geometries were simulated in ANSYS Fluent v16.1 using stainless steel as the device material with a thermal conductivity of 20 W/m-K, a heat transfer coefficient of 50 W/m2-K, and inlet velocities of 0.5 and 1.0 m/s for each fuel-air mixture. Temperature and velocity profiles for a methane-air reaction for each type of micro-combustor (constant-diameter, converging, diverging, converging-diverging, and backward-facing step) can be seen in Figure 3. Operating conditions for these simulations are u = 1.0 m/s and φ = 0.6. Noticeable in these profiles is that there is blowout of the flame for the converging and converging-diverging geometries at an inlet velocity of 1.0 m/s. In a comparison between the micro-combustors that do have stable flames, the diverging geometry creates a thinner and longer flame than those seen in the constant-diameter and backward-facing step geometries.
Also of note is the location of the flame for the backward-facing step micro-combustor: it has been anchored closer to the inlet plane than all other geometries for the same initial conditions. Lastly, it can be seen from the profiles that the temperatures measured at the micro-combustor outlet for the constant-diameter and diverging geometries are similar in magnitude. Although blowout of the flame has been sustained by the converging micro-combustor at this inlet velocity, it has produced the highest outlet temperature out of the five geometries. Simulations at an inlet velocity of 0.5 m/s were also completed to use as a comparison and are shown in Figure 4. As predicted, the decrease in inlet velocity has allowed flames to stabilize in all of the micro-combustor geometries. For the converging, diverging, and converging-diverging geometries the flames are more thin and elongated than those seen in the constant-diameter and backward-facing step micro-combustors. Similar to the simulation for an inlet velocity of 1.0 m/s, the backward-facing step geometry shows that the flame produced by the combustion process has been anchored close to the inlet. This behavior suggests that for a backward-facing step geometry higher inlet velocities could be used initially while still combusting the premixed fuel and air and producing a stable flame. Again it can be seen that the converging micro-combustor produces the highest exit temperature. Table 1 summarizes the maximum temperatures calculated for all the previously mentioned simulations at inlet velocities of 0.5 and 1.0 m/s. As inlet velocity is increased flame temperature in the micro- combustor increases in the constant-diameter, diverging, and converging-diverging geometries for all three fuels. The decrease in temperature seen in the converging micro-combustor with premixed ethane and air can be attributed to the blowout experienced with the higher inlet velocity. For the backward-facing step geometry the difference in temperature for inlet velocities of 0.5 and 1.0 m/s is approximately 2 K for the methane-air mixture,
Figure 3. Profiles of temperature at u = 1.0 m/s for (a) 1 mm × 10 mm constant-diameter; (b) converging; (c) diverging; (d) converging-diverging; and (e) backward-facing step geometries.
Figure 4. Profiles of temperature at u = 0.5 m/s for (a) 1 mm × 10 mm constant-diameter; (b) converging; (c) diverging; (d) converging-diverging; and (e) backward-facing step geometries.
which suggests that for the fuel at an equivalence ratio of 0.6 inlet velocity has little impact on flame temperature for this type of micro-combustor. The increase in temperature experienced by the backward-facing step geometry for hydrogen and ethane for these inlet velocities suggests that the higher velocity provides enough
Table 1. Maximum temperatures at 0.5 m/s and 1.0 m/s for different micro-combustor geometries.
circulation around the step geometry to create more complete combustion of the mixture. In comparison with the methane-air simulations at the same equivalence ratio it was found that hydrogen-air combustion has overall produced greater maximum temperatures for an inlet velocity of 1.0 m/s. However, for an inlet velocity of 0.5 m/s the methane-air mixture generated higher temperatures than hydrogen-air for the constant-diameter, diverging, and backward-facing step geometries. This result suggests that an inlet velocity of 0.5 m/s is not fast enough for the combustion to get started in the remaining geometries and create enough energy to raise the temperature of the products. For the ethane-air simulations at 1.0 m/s, the converging and converging-diverging geometries experienced blowout and subsequent quenching of the flame at this relatively low inlet velocity which shows how powerful the ethane-air reaction is at this scale. Similar to the results for methane and hydrogen, the diverging and backward-facing step geometries kept the flame produced anchored within the micro-combustor for the ethane-air mixture. These simulation results show that although the diverging micro-combustor geometry produces the highest maximum temperature for both inlet velocities for all fuel-air combinations in a stainless steel micro-combustor, the converging geometry yields higher exit temperatures than the other geometries tested. Figure 5 displays the temperature profiles for each fuel-air mixture in the converging micro-combustor. For the same initial conditions, it can be seen that fuel selection has a large impact on flame temperature, size, and position within the converging micro-combustor. Of the three fuels, the hydrogen-air mixture results in a reaction region closest to the inlet of the device. This is likely due to the high heat of combustion of hydrogen causing rapid reaction of the inlet species. Conversely, it is seen that using ethane, with the lowest heat of combustion, leads to slower reaction times and a maximum temperature region further downstream. For hydrogen-air combustion the converging geometry has allowed the flame temperature to increase approximately 110 K over the constant-diameter combustor. The ethane-air mixture produces the highest flame temperature in the micro-combustor, although for this configuration the flame has experienced blowout. Using a smaller inlet velocity would lead to flame containment for this configuration and therefore this fuel would yield the highest efficiencies. The difference between maximum temperatures obtained with the ethane and methane fuels was expected, although the slight difference between those obtained with methane and hydrogen (T < 1 K) was unexpected since the heat of combustion of hydrogen is so much greater than that of methane.
4.2. Fuel Performance
The influence of geometry on results from simulations completed with methane, hydrogen, and ethane fuels were presented above. In this section, we explore the effect of the fuel-to-air ratio. In each of the three cases, lean mixtures were simulated, in order to determine the best fuel for micro-combustion and the equivalence ratios that give maximum temperatures and stable flames. Fuel-lean equivalence ratios of 0.6, 0.7, 0.8, and 0.9 for mixtures in stainless steel constant-diameter micro-combustors of diameter 1 mm and length 10 mm were chosen. Material properties for stainless steel used in the following simulations are as follows: k = 20 W/m-K, h = 50 W/m2-K, e = 0.2 for the conductivity, coefficient of convection, and emissivity; respectively. Figure 6 shows the contours of temperature for the ethane-air mixture entering the micro-combustor at 0.5 m/s for the above
Figure 5. Profiles of temperature for converging micro-combustor for (a) CH4; (b) H2; and (c) C2H6.
Figure 6. Profiles of temperature for C2H6 with (a) φ = 0.6; (b) φ = 0.7; (c) φ = 0.8; and (d) φ = 0.9.
stated range of equivalence ratios. It can be seen that as the equivalence ratio is increased from 0.6 to 0.9 the maximum temperature of the lean fuel-air mixture also increases. A difference of approximately 540 K is seen in the maximum temperature between simulations of φ = 0.6 and φ = 0.9. For the entire range of equivalence ratios the flames have become stable at about the same distance away from the micro-combustor inlet. This suggests that increasing equivalence ratio has no effect on flame location within the micro-combustor for premixed ethane and air combustion. All flames are stable within the 1 mm × 10 mm micro-combustor for the range of equivalence ratios, and flame shape is also not impacted by increasing fuel content of the mixture. Simulations of the methane-air combustion for equivalence ratios of 0.6, 0.7, 0.8, and 0.9 were conducted for an inlet velocity of 0.5 m/s and are shown in Figure 7. Similarly to the ethane-air simulations, the largest maximum temperature occurs for an equivalence ratio of 0.9. As equivalence ratio is increased the position of the flame inside the micro-combustor moves closer to the inlet plane. In comparison to an inlet velocity of 1.0 m/s, it is important to note that for half the inlet velocity prescribed maximum temperatures decrease only in the approximate range of 50 K - 65 K. A graph depicting maximum temperature as a function of equivalence ratio at u = 1.0 m/s for each fuel is presented in Figure 8. This inlet velocity was chosen because it produced the highest maximum temperatures in the constant-diameter micro-combustor for each equivalence ratio, although these trends were observed at all inlet velocities tested.
As predicted, as the equivalence ratio for all three fuels is increased the maximum temperature calculated by the simulations also increases. A larger fuel content of the fuel-air mixture allows for more combustion and thus
Figure 7. Profiles of temperature for CH4 with (a) φ = 0.6; (b) φ = 0.7; (c) φ = 0.8; and (d) φ = 0.9.
Figure 8. Temperature vs. equivalence ratio in a 1 mm × 10 mm micro-combustor at u = 1.0 m/s.
higher measured temperatures. Since an equivalence ratio of 0.9 yields the largest maximum temperatures for each fuel, a qualitative comparison can be made from Figure 9, which shows temperature profiles for each fuel- air mixture at u = 0.5 m/s and φ = 0.9. The temperature profiles show how the ethane-air mixture provides a much greater maximum temperature compared to methane and hydrogen. For identical initial conditions, the flame for premixed ethane and air has stabilized further downstream in the micro-combustor than for the methane and hydrogen simulations.
4.3. Material Performance
Lastly, material selection was investigated for micro-combustion using three different materials: stainless steel, aluminum oxide, and quartz. For each material, a 1 mm × 10 mm constant-diameter micro-combustor with a 0.2 mm thick wall was simulated with methane-air, hydrogen-air, and ethane-air mixtures at an equivalence ratio of 0.6. The heat transfer coefficient was varied for each material-fuel combination in order to study the effect on maximum temperature, flame shape, and flame location. Values of 5, 10, and 50 W/m2-K were chosen in order
Figure 9. Profiles of temperature at u = 0.5 m/s and φ = 0.9 for (a) CH4-air; (b) H2-air; and (c) C2H6-air.
to quantitatively and qualitatively compare results for environments with light and strong forced convection, as well as natural convection. Early on in the simulations it was determined that the flame temperature increases with decreases in the heat transfer coefficient. Therefore natural convection was found to be the optimal operating condition for a micro-combustor: the lower the heat transfer coefficient the less heat loss experienced across the walls of the device. Temperature profiles of the stainless steel micro-combustor with a mixture of methane and air at φ = 0.6 and a heat transfer coefficient of 5 W/m2-K at several inlet velocities are presented in Figure 10. The profiles show that with the constant heat transfer coefficient the prescribed inlet velocity has an effect on the maximum temperature calculated in the micro-combustor, which agrees with preceding simulations. With increasing velocity the temperature of the flame produced by the combustion of the methane and air also increases. In addition, as inlet velocity is varied the shape of the flame created by the combustion process becomes thinner and longer, which agrees with previous results in which the velocity is increased. In order to gain more insight into material selection, simulations of a 1 mm × 10 mm micro-combustor made of aluminum oxide were completed for each fuel-air combination. Temperature profiles of those simulations at an inlet velocity of 1.0 m/s are presented in Figure 11. The ethane-air mixture again produces the highest flame temperature out of the three fuel choices. These profiles once more show for a specified inlet velocity that premixed hydrogen and air forms a stable flame closer to the inlet of the micro-combustor than the hydrocarbon fuels. For more comparison Figure 12 below shows temperature profiles of a quartz micro-combustor at the same initial conditions as above. Compared to the aluminum oxide micro-combustor, the quartz micro-combustor produces maximum temperatures that are quite similar in magnitude. The difference in temperature between the aluminum oxide and quartz micro-combustors for ethane-air combustion is only about 20 K. Due to this slight difference between the two materials, it was concluded that both materials are sufficient for micro-combustor materials. However, because the aluminum oxide micro-combustor produced the higher flame temperatures, it was chosen to be the best material for micro-combustor design.
4.4. Micro-Combustor Efficiency
In an effort to put a numerical value on what constitutes the best micro-combustor design, overall combustor efficiency was calculated using the following equation:
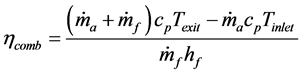 (1)
(1)
where 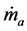 is the mass flow rate of air,
is the mass flow rate of air, 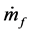 is the mass flow rate of fuel, cp is the specific heat at constant pressure, Texit and Tinlet are the exit and inlet temperatures, respectively, and hf is the heating value of the fuel. Since ethane has been proven to generate the highest maximum temperatures of the three fuels tested, combustor efficiencies for ethane-air simulations with a heat transfer coefficient of 5 W/m2-K and equivalence ratio of 0.9 were calculated and are presented in Table 2 for an aluminum oxide combustor. Surprisingly, the constant- diameter micro-combustor made of aluminum oxide yielded the highest flame temperature. However, this is not necessarily an indicator that this micro-combustor configuration will produce the highest efficiency since it is
is the mass flow rate of fuel, cp is the specific heat at constant pressure, Texit and Tinlet are the exit and inlet temperatures, respectively, and hf is the heating value of the fuel. Since ethane has been proven to generate the highest maximum temperatures of the three fuels tested, combustor efficiencies for ethane-air simulations with a heat transfer coefficient of 5 W/m2-K and equivalence ratio of 0.9 were calculated and are presented in Table 2 for an aluminum oxide combustor. Surprisingly, the constant- diameter micro-combustor made of aluminum oxide yielded the highest flame temperature. However, this is not necessarily an indicator that this micro-combustor configuration will produce the highest efficiency since it is
Figure 10. Profiles of temperature at φ = 0.6 and h = 5 W/m2-K for (a) u = 0.3 m/s; (b) u = 0.5 m/s; (c) u = 0.8 m/s; and (d) 1.0 m/s.
Figure 11. Profiles of temperature in an aluminum oxide micro-combustor at u = 1.0 m/s, φ = 0.6, and h = 5 W/m2-K for (a) CH4-air; (b) H2-air; and (c) C2H6-air.
Figure 12. Profiles of temperature in a quartz micro-combustor at u = 1.0 m/s, φ = 0.6, and h = 5 W/m2-K for (a) CH4-air; (b) H2-air; and (c) C2H6-air.
Table 2. Maximum temperatures for C2H6-air combustion in different micro-combustor geometries.
Table 3. Efficiencies for C2H6-air combustion in different micro-combustor geometries.
dependent on the exit temperature measured at the outlet. Blowout of the flame was experienced by several configurations, as indicated by the decrease in the maximum temperature as inlet velocity is increased. Below in Table 3 are the calculated efficiencies for each ethane-air case; the exit temperatures were all measured at themicro-combustor outlet along the symmetry plane using CFD Post v16.1.
The efficiencies calculated for these simulations are fairly low for a micro-combustor: as previously mentioned, Waitz, Gauba, and Tzeng [11] computed micro-combustor efficiencies of 70% - 90% in their study using premixed hydrogen and air. The highest efficiencies calculated belong to the converging geometry, and it should be mentioned that for the 0.8 and 1.0 m/s inlet velocities blowout of the flame occurs. Therefore the aluminum oxide converging micro-combustor with a prescribed inlet velocity of 0.5 m/s yields the maximum efficiency (7.63%) in these simulations. There are several parameters that can be changed that would result in an improvement in efficiency, including the mass flow rate and the specific heat of the fuel-air mixture, assumed to be constant. Increases in the air and fuel mass flow rates can be achieved by an increase in either the inlet velocity or inlet cross-section area. However, an increase in inlet velocity in some of the proposed micro-combustor geometries could cause quenching and blowout of the flame and lead to lower exit temperatures, while increasing the inlet area hardly affects the efficiency calculation. Increasing the specific heat of the mixture by way of increasing the equivalence ratio would also improve efficiency, but again by very little. This indicates that it would be difficult to increase combustor efficiency without directly increasing the exit temperature.
5. Conclusion
In order to determine the best design for a micro-combustor, several considerations were taken into account, such as the type of fuel used, geometry, and material selection. A series of CFD simulations were completed for different micro-combustor design configurations using ANSYS Fluent v16.1. From the analysis of results with methane-, hydrogen-, and ethane-air mixtures it was determined that ethane was the best fuel choice due to its high thermal energy output at lower inlet velocities. As far as micro-combustor geometry is concerned, the diverging combustor produced the highest maximum flame temperatures while the converging geometry gave the highest exit temperatures. Since combustor efficiency is directly related to the difference between inlet and outlet temperatures, the converging geometry proved to be the best choice. Finally, three combustor design materials were tested: stainless steel, aluminum oxide, and crystal quartz. Of these materials, aluminum oxide allowed less heat loss to the surrounding environment for the same initial conditions. It was determined that an aluminum oxide converging micro-combustor with premixed ethane and air at an equivalence ratio of 0.9, inlet velocity of 0.5 m/s, and heat transfer coefficient of 5 W/m2-K returned the highest combustor efficiency of cases considered. Although earlier experimental and computational research on the performance characteristics of converging micro-combustors is limited, our study suggests that further investigations should be undertaken in order to determine if this type of geometry is feasible for micro-combustion and micro-power generation.
Cite this paper
Leigh T. Powell,Ralph C. Aldredge, (2016) Design Optimization of a Micro-Combustor for Lean, Premixed Fuel-Air Mixtures. Journal of Power and Energy Engineering,04,13-26. doi: 10.4236/jpee.2016.46003
References
- 1. Kaisare, N.S. and Vlachos, D.G. (2012) A Review on Microcombustion: Fundamentals, Devices and Applications. Progress in Energy and Combustion Science, 38, 321-359.
http://dx.doi.org/10.1016/j.pecs.2012.01.001 - 2. Khandelwal, B. and Kumar, S. (2010) Experimental Investigations on Flame Stabilization Behavior in a Diverging Micro Channel with Premixed Methane-Air Mixtures. Applied Thermal Engineering, 30, 2718-2723.
http://dx.doi.org/10.1016/j.applthermaleng.2010.07.023 - 3. Norton, D.G. and Vlachos, D.G. (2003) Combustion Characteristics and Flame Stability at the Microscale: A CFD Study of Premixed Methane/Air Mixtures. Chemical Engineering Science, 58, 4871-4882.
http://dx.doi.org/10.1016/j.ces.2002.12.005 - 4. Zarvandi, J., Tabejamaat, S. and Baigmohammadi, M. (2012) Numerical Study of the Effects of Heat Transfer Methods on CH4/(CH4+H2)-AIR Pre-Mixed Flames in a Micro-stepped Tube. Energy, 44, 369-409.
http://dx.doi.org/10.1016/j.energy.2012.06.015 - 5. Bagheri, G., Hosseini, S.E. and Wahid, M.A. (2014) Effects of Bluff Body Shape on the Flame Stability in Premixed Micro-Combustion of Hydrogen-Air Mixture. Applied Thermal Engineering, 67, 266-272.
http://dx.doi.org/10.1016/j.applthermaleng.2014.03.040 - 6. Epstein, A.H., Senturia, S.D., Anathasuresh, G., Ayon, A., Breuer, K., Chen, K-S, Ehrich, F.E., Gauba, G., Ghodssi, R., Groshenry, C., Jacobson, S., Lang, J.H., Lin, C.-C., Mehra, A., Mur Miranda, J.O., Nagle, S., Orr, D.J., Piekos, E., Schmidt, M.A., Shirley, G., Spearing, S.M., Tan, C.S., Tzeng, Y.-S. and Waitz, I.A. (1997) Power MEMS and Microengines. Proceedings of IEEE Transducers '97 Conference, Chicago, June 1997.
- 7. Chao, Y.-C., Chen, G.-B., Wu, C.-Y. and Chen, C.-P. (2006) Development of a Catalytic Hydrogen Micro-Propulsion System. Combustion Science and Technology, 178, 2039-2060.
http://dx.doi.org/10.1080/00102200600793395 - 8. Murali, P.B. (2014) Simulation Studies of Premixed CH4/Air Microcombustion. International Journal of Engineering Research and Applications, 4, 96-102.
- 9. Yang, W., Deng, C., Zhou, J., Liu, J., Wang, Y. and Cen, K. (2014) Experimental and Numerical Investigations of Hydrogen-Air Premixed Combustion in a Converging-diverging Micro Tube. International Journal of Hydrogen Energy, 39, 3469-3476.
http://dx.doi.org/10.1016/j.ijhydene.2013.12.102 - 10. Turns, S.R. (2006) Thermal-Fluid Sciences: An Integrated Approach. Cambridge UP, Cambridge.
- 11. Waitz, I.A., Gauba, G. and Tzeng, Y.-S. (1998) Combustors for Micro-Gas Turbine Engines. Journal of Fluids Engineering, 120, 109-117.
http://dx.doi.org/10.1115/1.2819633 - 12. Li, J., Chou, S.K., Huang, G., Yang, W.M. and Li, Z.W. (2009) Study on Premixed Combustion in Cylindrical Micro Combustors: Transient Flame Behavior and Wall Heat Flux. Experimental Thermal and Fluid Science, 33, 764-773.
http://dx.doi.org/10.1016/j.expthermflusci.2009.01.012














