Journal of Power and Energy Engineering
Vol.04 No.08(2016), Article ID:69442,12 pages
10.4236/jpee.2016.48003
Passive Study of Energy Efficiency of a Building with PCM on the Roof during Summer in Casablanca
Amina Mourid, Mustapha El Alami*, Mostafa Najam
Laboratory of Physics of Materials, Microelectronics, Automation & Thermal (LPMMAT), Department of Physics, Faculty of Sciences Ain Chock, Hassan II University of Casablanca, Casablanca, Morocco

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 April 2016; accepted 30 July 2016; published 3 August 2016
ABSTRACT
Energy efficiency in buildings is today a prime objective for energy policy at national and international levels. Because the residential and commercial energy consumption has steadily increased reaching figures between 20% and 40%. The use of thermal insulation of the building envelope is one of the most currently requested solutions to reduce this energy consumption. Phase Change Materials (PCM) have received increased attention due to their ability to store large amounts of thermal energy within narrow temperature ranges. This property makes them ideal for storage of passive heat in the building envelopes. An experimental study was conducted to analyze the influence of PCM in the construction of exterior walls. Two test cells are constructed in the Faculty of Science Ain Chock, Casablanca. One is equipped with a 0.56 cm layer of PCM on its roof while the second is a reference cell without PCM. The results presented for the period from 8th to 10th July 2014 show that the integration of PCM layer reduces the amplitude of instantaneous heat flux through the horizontal wall. The indoor and the internal vertical wall temperatures, in the case of the cell with PCM, are relatively decreased compared to those of the reference one. For example, the maximum deviation between the indoor temperatures of the cubicles is not more than 1.5˚C while the one on the west faces reaches 3˚C by mid day. Also the inclusion of a layer of PCM shifts the time of peak load and discharge.
Keywords:
Energy Efficiency, Experimental Study, PCM, Solar Radiation Insulation, Summer, Casablanca

1. Introduction
The energy consumption is expected to increase rapidly in the coming years due to the significant development of the building sector as well as the significant increase in household equipment rate appliances. The Moroccan policy framework is focused on reducing energy consumption in the building sector and so thermal insulation in buildings is imposed as an important factor to achieve thermal comfort for the occupants and to reduce unwanted heat loss or gain. The aim is to reduce the energy consumptions. Note that housing and tertiary (hospitals, hotels…) are responsible for, approximately, 25% of the total energy consumption in Morocco [1] . One such method is to incorporate PCM to the lightweight buildings. Phase Change Materials are smart materials that are based on a simple physical principle: they liquefy absorbing energy from a certain temperature characteristic for each type of materials (generally determined by their chemical formulation), and restore the energy when the temperature of their environment decreases.
When selecting a PCM, its melting and freezing temperatures should be close to the range of the average room air temperature. Then many factors influence the choice of the PCM: weather, building structure and thermos-physical proprieties [2] .
The use of phase change materials has been studied since the 1940s [3] [4] . However, their usage in building has been the subject of several studies. Kuznik et al. [5] examined the effect of integration of PCM wallboard in the lateral walls and the ceiling of renovated tertiary building. Two identical rooms have been tested: The first as reference and the second was equipped with an ENERGAIN PCM. This later was characterised by the authors using Differential Scanning Calorimeter Method (DSC). It was reported that its melting and freezing temperatures were 13.6˚C and 23.5˚C, respectively. The results showed that the PCM enhanced the thermal comfort of occupants. They concluded, too, that the thermal comfort improvement could be efficient if the building was of low thermal inertia and if the temperature variations were around the phase change temperature of used PCM. An energetic and economic study related to the application of PCMs Boards in building enclosures was conducted by Sun et al. [6] . In this study, the solar energy stored by PCM in the day is recovered at night either naturally using outside air, or by using cooling systems that consume electrical energy (less expensive during the night). They developed a heat transfer model to analyse electric energy consumption during the cooling season for five different climate regions in China. Energy saving ration and simple payback period were used to assess the simulation application. Their results showed that the energy saving ratio was 100% when a cold energy source was used and then the use of PCMs did not offer economic benefit from reduced air conditioning. An acceptable payback period was obtained the phase change temperatures were 3˚C higher than mean outdoor temperature. Lee et al. [7] studied thermal performance of building walls integrating PCMs. Heat reduction and heat transfer time delay were evaluated in this work. The PCM was incorporated as thin layers placed longitudinally within the walls at different depths. Note that this study was realized experimentally using two test houses and concerning the thermal performance of the south and west facing walls with and without PCMs. Five positions of PCM layer was examined (1 to 5 from inside to outside) at intervals of 1.27 cm. The results showed that the optimal location of PCM layer (location for which heat transfer reduction was maximum) in the south wall was 2.54 cm and that in the west wall was 1.27 cm from the wallboard. Peak heat flux reductions were 51% and 29.7%, at these locations, for the south wall and the west wall, respectively. The maximum heat flux time delays were 6.3 h (PCM placed at the wallboard) for the south wall and 2.3 h in the west wall (PCM located at 1.27 cm from the wallboard). Thermal performance of a PCMTS was evaluated, using a dynamic wall simulator, by Jin et al. [8] . In this work authors used a mixture of gypsum and PCMs (10% by weight of PCMs). They developed a PCM layer integrated into a prototype walls and they evaluated the thermal performance of this system in three different locations within the cavity of a typical North American building walls. The experimental results showed that, compared to a wall without PCMTS, the peak heat fluxes were reduced by as much as 11% when the thermal shield was placed in the inward-most location next to the internal face of the gypsum wallboard within the wall cavity. The PCM thermal shield produced only small effects on the peak heat fluxes when it was placed half way between the enclosing surfaces of the internal cavity of the wall and almost no effect when it was placed next to the internal face of the outermost layer of the wall.
Two identical cells with Vacuum Insulation Panels (VIP) light wallboards with and without PCM were studied by Ahmad et al. [9] . Temperature and heat flux were determined and compared to a numerical simulation with TRNSYS software. The study showed that the PCM could reduce the indoor temperature amplitude. In Lleida (Spain), Castell et al. [10] tested several cubicles that were made with conventional and alveolar brick. Two different microencapsulated PCMs (SP-25 A8 (hydrate Salt with melting point 26˚C) and RT-27 (paraffin, melting temperature 28˚C) provided by RUBITHERM) were added to the cubicles. Two different experiments were performed: the first measuring the indoor temperature and the second measuring the consumption when domestic heat pumps controlled the inner temperature for the cubicles. The temperatures in the cubicles with PCM were reduced compared with the cubicle without PCM and the energy consumption of the cavities using RT-27+PU was reduced about 15% compared to cells with PU, while the cavities with the SP-25+Alveolar had achieved 17% of energy reduction, compared to cubicle with alveolar one.
In a large scale, Mandilaras et al. [11] studied a two-story typical family house in mid-west Greece, which incorporated gypsum panels with PCM. Experimental measurements performed with an unoccupied house showed that the indoor air temperatures, in all thermal zones of the building, do not significantly vary during a 24 h day-night cycle, leading to a decrease in the decrement factor and an increase in the time lag.
The objective of this study is to evaluate the thermal performance of residential walls equipped with a phase change material on the roof during summer 2014. The experimental set-up consists of two identical cells built at the Faculty of Science Ain Chock Casablanca.
2. Experimental Setup
The experimental set-up consists of two cells, kind of living rooms, located at the Faculty of Science Ain Chock (FSAC), Hassan II University of Casablanca, Figure 1(a). The first sample (reference cavity) is made with standard walls, and the other one is equipped with PCM on the roof. They are equipped with 75 Thermocouples K-Type (2/10 mm). The assembly is connected to a data acquisition as shown in Figure 1(b).
2.1. Phase Change Material (PCM)
The phase change material (PCM) used is Energain product qualified by Dupont de Nemours (Luxembourg) company. The product in the form of panel consisting of two aluminium sheets 130 μm thick is composed of a solid compound copolymer (ethylene, 40%) and paraffin (60%).
The panels have dimension of 1 m × 1.2 m × 0.00526 m and melting temperature of PCM (paraffin) is 21.7˚C, an enthalpy of 70 kJ/kg. The thermal conductivity is 0.18 Wm−1∙K−1 in the solid phase and decreases to about 0.14 Wm−1∙K−1 in liquid phase. The Energain panel 5 mm thickness is equivalent to 30 mm of concrete as a function of temperature. The choice of this PCM is mainly dictated by its melting temperature, which is close to human comfort and its availability in the market.
2.2 Test Cells
The cavities have dimensions of 3 m × 3 m × 3 m, Figure 1(a). The north wall is equipped with a laminated wooden door (1 m × 2 m) and a single glazed window (1 m × 1 m). The vertical walls have a thickness of 30.62 cm and are composed of five layers (1 cm of mortar, 7 cm of alveolar yellow brick, 14 cm of air layer, 7 cm of alveolar yellow brick and 1 cm of mortar). The outer face of the roof is covered with PCM panels. Thus, the ceiling is composed of the following layers (from inside to outside): 2 cm of mortar, 12 cm of heavy concrete, 2 cm of mortar and 0.526 cm of PCM.
2.3. Instrumentation and Measurements
The cells are instrumented with thermocouples K-type (2/10 mm) in each wall. They are, carefully, welded,
Figure 1. Experimental setup. (a) View of the cell; (b) Figure of the experiment: PCM on the roof; (c) PCM Panel.
ensuring that the weld is of the same diameter that the two wires. Then, they are calibrated and connected to multiplexers in the data acquisition device. The absolute thermal errors (ϴmeasured-ϴSet point) do not exceed 0.1˚C. The thermocouples are distributed in order to access to the average temperatures of all the walls and the indoor temperature of the samples.
Note that, achieving temperatures and heat flux measurements in a cell at the scale 1 in-situ is facing a serious control problem of boundary conditions. They are conditioned by the weather conditions of the site, which vary considerably with time.
We recall that experimental determination of the thermal resistance of walls always presents practical problems in the field for thermal analysis as well as for the determination of energy savings. In recent years, experimental activity has been conducted solely in the laboratory using prototypes of walls built with reduced scale. In particular, the test facility designed and built prototypes based on directives that met the objectives of a large set of international standards [12] . Measurements of both surface temperatures and heat flux related to a wall in steady state conditions were thus determined. Also, one must to consider that, notwithstanding the extreme accuracy of the measurement in the laboratory, the thermal resistance of the wall determined in-situ might present a significant deviation from the resistance determined from the prototype. This deviation is due not only to the inevitable differences among supplies of the same material made in different time periods, but also to the inevitable differences in the conditions of wall-building [13] .
In our procedure, we chose the period from 8th to 10th July in this study, because it shows some moderation in Casablanca weather fluctuations, compared to other periods of summer.
2.4. Weather Data
The cavities are located in Casablanca FSAC (33˚32'N latitude, 7˚39'W longitude and altitude 57 m). The weather data used in this study are those relating to 8th to10th July 2014, measured using our weather station installed on the roof of the FSAC. These data were measured with a time step of one hour and concerning: Outdoor temperature, humidity, global solar radiation, wind speed and wind direction. Note that for this period, external temperature fluctuations are not very important and do not exceed 6˚C as shown in Figure 2. Global heat radiation is presented in Figure 3. It is practically identical for the three days of measurement. It maximum value is around 850 W/m2. Against, the wind speed has varied considerably between the nights of 8th to 9th July, Figure 4. These fluctuations will act on the outer heat exchange coefficient and thus the thermal resistance of the walls.
3. Equations
The equation used to calculate the thermal resistance for different walls is as follows:
Figure 2. Outdoor temperature, 8th to 10 July 2014.
Figure 3. Solar radiation (W/m2), 8th to 10 July 2014.
Figure 4. Wind Speed variation, 8th to 10 July 2014.
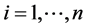
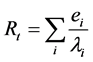 (1)
(1)
n: number of the wall layers.
However, in large spaces such as wall cavities, heat can still be lost across the air layer (inside the wall) by convection and radiation.
Table 1 summarizes the calculation of the thermal resistance of the various walls taking into account their composition.
The thermal conductivity of air is about 0.026 W/m∙K, the value 0.09 W/m∙K, considered in this work (Table 1, found in TRNSYS16 database) reflects the weak natural convection that may exist in the layer air.
The heat flux exchanged is calculated relating to the overall strength taking into account the internal natural convection and the external free convection:
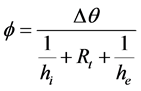 (2)
(2)
Table 1. Characteristics of the different layers of the walls.
The thermal convective heat transfer coefficient describing heat exchanged along the external and internal faces of the building walls, can be calculated using approximated correlations from previous work [14] [15] , respectively:
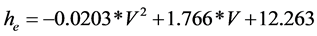 (W∙m2∙K−1) (3)
(W∙m2∙K−1) (3)
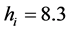 (W∙m2∙K−1) (4)
(W∙m2∙K−1) (4)
4. Results and Discussion
In order to minimize the heat gain in the summer period, we placed the PCM on the roof of the test cell. To highlight the contribution of PCM for insulation against the solar radiation and storage, we performed a systematic comparison of the internal and external temperatures of the walls and the room temperature with and without PCM. The preliminary results presented in this paper are obtained for the period from 8th to 10th July 2014, for which we consider that the boundary conditions are fairly stable and uniform in order to use the steady state method in our evaluation process of thermal resistance.
Thermal Profiles
Figure 5 and Figure 6 illustrate the temperature variations of west and south walls of the two cavities, respectively. These walls are exposed to solar radiation more than the other plates. In case of the west wall of the sample with PCM (Figure 5), the temperature of the inside surface is lower than the inner temperature of the same wall of that without PCM, during the day. The situation is reversed during the night. It turns that the integration of PCM on the roof can reduce the temperature fluctuations of 2.53˚C during our test period. Figure 6 shows that the external temperature fluctuated from 20.70˚C to 31.56˚C and the internal temperature is varying between a minimum of 25.67˚C and a maximum of 29.01˚C for the cavity with PCM while in the case without PCM, it varies from 25.7˚C to 30.04˚C, during these three days. The incorporate PCM in the ceiling allows a reduction of the temperature for different walls of the cavity (different orientations).
Moreover, we can observe a remarkable difference between the surface temperatures of west wall and that of the south wall, in both cases (with and without PCM), it is due to the significant insolation received by the south faces.
The variation of the indoor temperature of the two cells (with and without PCM) is shown in Figure 7. It is found that the indoor temperature of the cubicle with PCM is reduced by 1.5˚C compared to the one without PCM. This can be explained by the good thermal inertia presented by the phase change material (PCM). This difference between indoor temperatures is directly affecting the comfort sensation, according the well-estab- lished comfort theories. In Table 2 we summarized the thermal time shifts for the cell walls.
The reduction of heat inputs through the ceiling (by introduction of the PCM) does not only affect the
Figure 5. Evolution of the external and internal temperatures of the west face of the two cavities.
Figure 6. Evolution of the external and internal temperatures of the south face of the two cavities.
temperature of the walls but also the indoor temperature of the cell. The latter is the result of heat exchange between the cavity and the outside through the walls (usually it is calculated by weighting temperatures of different surfaces). The latter (walls) are at different temperatures, for given time (depending on their orientation). The differences that present the wall temperatures for both cavities are not synchronized (when the difference related to the southern walls is low, that of the East walls are important and so on). Knowing that the indoor temperatures are closely related to those of the walls at a specific time, it is normal that the gap between them will not be comparable to those of walls.
Figure 7. Evolution of the indoor temperatures of the cavities.
Table 2. Time shifts between the temperatures of the two cells.
We present the heat transfer between the two cavities and the outside in terms of heat flux densities through the various walls. In this paper, only those relating to the ceilings, the west and the south walls will be exposed and discussed.
Figure 8 shows the heat flux evolution of the two ceilings with and without PCM. First, we note that, there is a significant gap between the two heat flux densities during this period. The insulation effect of PCM is clearly visible during the day as can be seen on the maximum curve (φmax, with_PCM = 58.35 W/m2, φmax, without_PCM = 63.80 W/m2). The Aluminium layer reflects a significant portion of solar radiation in our setup. It will reduce, significantly, the solar flux absorbed by the PCM, knowing its reflectivity against the radiation which is about 0.9. In this work, we have not considered this aspect because our objective was focused on the study of the thermal efficiency of the local, but we evaluated the effect of the entire PCM panel. In further configurations, we will cover the panels by a very few reflector materials to highlight the only effect of PCM. The effect of the thermal inertia is very clear; a delay of three hours is observed (Table 2). This leads to a significant reduction in energy consumption during the discharge period (night). The cells do not cool in the same way. In fact, the heat flux density on the cell with PCM remains greater than or equal to zero while that of the reference cell drops to −10 W/m2. This is due to the refund of the amount of heat previously stored (in the form of latent heat) in the PCM.
Based on the analysis of representative figures of the heat flux exchanged through the vertical walls, we distinguish the emergence of two phenomena during the day. As an example, we present Figure 9 and Figure 10 showing heat fluxes related to the West and South walls of the two cavities. Generally, it is noted that the heat flux values range from maximum (positive) and minimum (negative) for a period of 24 hours. From 6 h 00 to 13 h 00 both cells yield the same heat flux density while for the rest of the day, the exchanged heat flux are different
Figure 8. Evolution of the heat flux densities of ceilings with and without PCM.
Figure 9. Evolution of the heat flux densities of west wall for the two cavities.
from one cell to the other one. Through the west wall, the maximum value in the cavity without PCM is 2.98 W/m2, while in the cell with PCM; it reaches 2.62 W/m2. This remark also applies to the south wall. We can note also that the time shift is approximately 6 hours for the two walls. So it is an important thermal inertia introduced by the PCM.
During the first period, the similarity of the heat flux is due to internal wall temperatures, which are substantially equal. The difference observed in the second period is due to the time shift between the internal and external temperatures of the two cells (see Figure 2 and Figure 3).
Figure 10. Evolution of the heat flux densities of south wall for the two cavities.
The heat flux through the ceiling is almost 10 times greater than those for vertical faces. The difference of the heat fluxes of the two ceilings arrives to 11.2 W/m2. This suggests the importance of the ceiling insulation against solar radiation in Morocco.
5. Conclusions
We conducted an experimental study of the thermal performance of two cavities like living quarters built, in-situ within the Faculty of Science Ain Chock, Casablanca. One of them is equipped with a PCM on the roof, during summer of 2014.
The results show that the integration of PCM on the roof of the building reduces the indoor temperatures of the cells by 1.5˚C and those of the internal walls of 2.53˚C. We also note that the amplitude of thermal oscillations of south and west walls decreases.
The study of heat transfer, through the vertical walls and ceilings of the two cells, led to conclude that the PCM was a good insulation and storage agent on the one hand, and greatly increased the thermal inertia of the cavity with PCM, on the other hand (due to the return of the heat stored during the day).
According to the same study, it is imperatively important to insulate the ceilings of residential premises against solar radiation: the gap between the two streams of the ceiling with and without PCM reaches 11.2 W/m2. Note that solar radiation constitutes the major part of the overall gain in Morocco. Therefore, there will be a significant reduction of energy used to cool the local. Furthermore, there is a significant time shift presented by the temperatures and the heat flux densities due to PCM incorporated in the ceiling.
Acknowledgements
Authors acknowledge the financial support provided by IRESEN “Institut de Recherche en Energie Solaire et Energies Nouvelles” Morocco.
Cite this paper
Amina Mourid,Mustapha El Alami,Mostafa Najam, (2016) Passive Study of Energy Efficiency of a Building with PCM on the Roof during Summer in Casablanca. Journal of Power and Energy Engineering,04,26-37. doi: 10.4236/jpee.2016.48003
References
- 1. (2012) Règlement Thermique de Construction au Maroc, Version simplifiée. Agence de Développement des Energies Renouvelables et de l’Efficacité Energétique, ADEREE.
- 2. Darkwa, K., O’Callaghan, P.W. and Tetlow, D. (2006) Phase-Change Drywalls in a Passive-Solar Building. Apply Energy, 83, 425-435.
http://dx.doi.org/10.1016/j.apenergy.2005.05.001 - 3. Telkes, M. (1949) Review of Solar House Heating. Heating and Ventilating, 46, 68-74.
- 4. Telkes, M. and Raymond, E. (1949) Storing Solar Heat in Chemicals. Heating and Ventilating, 46, 79-86.
- 5. Kuznik, F., Virgone, J. and Johannes, K. (2011) In-Situ Study of Thermal Comfort Enhancement in a Renovated Building Equipped with Phase Change Material Wallboard. Renewable Energy, 36, 1458-1462.
http://dx.doi.org/10.1016/j.renene.2010.11.008 - 6. Sun, X.Q., Zhang, Z., Medina, M.A. and Lee, K.O. (2014) Energy and Economic Analysis of a Building Enclosure Outfitted with a Phase Change Material Board (PCMB). Energy Conversion and Management, 83, 73-78.
http://dx.doi.org/10.1016/j.enconman.2014.03.035 - 7. Lee, K.O., Medina, M.A., Raith, E. and Sun, X.Q. (2015) Assessing the Integration of a Thin Phase Change Material (PCM) Layer in a Residential Building Wall for Heat Transfer Reduction and Management. Applied Energy, 137, 699-706.
http://dx.doi.org/10.1016/j.apenergy.2014.09.003 - 8. Jin, X., Medina, M.A. and Zhang, X.S. (2014) On the Placement of a Phase Change Material Thermal Shield within the Cavity of Building Walls for Heat Flux Reduction. Energy, 73, 780-786.
http://dx.doi.org/10.1016/j.energy.2014.06.079 - 9. Ahmad, M., Bontemps, A., Sallée, H. and Quenard, D. (2006) Thermal Testing and Numerical Simulation of a Prototype Cell Using Light Wallboards Coupling Vacuum Isolation Panels and Phase Change Material. Energy and Buildings, 38, 673-681.
http://dx.doi.org/10.1016/j.enbuild.2005.11.002 - 10. Castell, A., Martorell, I., Medrano, M., Pérez, G. and Cabeza, L.F. (2010) Experimental Study of Using PCM in Brick Constructive Solutions for Passive Cooling. Energy and Buildings, 42, 534-540.
http://dx.doi.org/10.1016/j.enbuild.2009.10.022 - 11. Mandilaras, I., Stamatiadou, M., Katsourinis, D., Zannis, G. and Founti, M. (2013) Experimental Thermal Characterization of a Mediterranean Residential Building with PCM Gypsum Board Walls. Building and Environment, 61, 93-103.
http://dx.doi.org/10.1016/j.buildenv.2012.12.007 - 12. ISO Standard 8301-1991. Thermal Insulation—Determination of Steady-State Thermal Resistance and Related Properties—Heat Flow Meter Apparatus.
- 13. Laurenti, L., Marcotullio, F. and de Monte, F. (2004) Determination of the Thermal Resistance of Walls through a Dynamic Analysis of In-Situ Data. International Journal of Thermal Sciences, 43, 297-306.
http://dx.doi.org/10.1016/j.ijthermalsci.2003.08.007 - 14. Zhang, L., Zhang, N., Zhao, F.Y. and Chen, Y.M. (2004) A Genetic-Algorithm-Based Experimental Technique for Determining Heat Transfer Coefficient of Exterior Wall Surface. Applied Thermal Engineering, 24, 339-349.
http://dx.doi.org/10.1016/j.applthermaleng.2003.07.005 - 15. Kaynakli, O. (2008) A Study on Residential Heating Energy Requirement and Optimum Insulation Thickness. Renewable Energy, 33, 1164-1172.
http://dx.doi.org/10.1016/j.renene.2007.07.001
Appendix
Nomenclature
e: Thickness, mm.
he: Outdoor thermal convective heat transfer coefficient (W/m2∙K).
hi: Inside thermal convective heat transfer coefficient (W/m2∙K).
PCM: Phase Change Material.
r: Thermal resistance of a wall layer (m2/W∙K).
Rt: Global thermal resistance of wall (m2/W∙K).
Δθ: Temperature gap (ϴwi-ϴwe) (˚C).
Δts: Thermal Time shift.
f: Heat flux, W/m2.
λ: Thermal conductivity (W/m∙K).
ϴwi: Internal temperature of the wall (˚C).
ϴwe: External temperature of the wall (˚C).
Subscripts
i: internal.
e: external.
max: maximum.
min: minimum.
we: external face of wall.
wi: internal face of wall.
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
NOTES
*Corresponding author.
















