Journal of Power and Energy Engineering
Vol.03 No.11(2015), Article ID:61285,8 pages
10.4236/jpee.2015.311003
A Strategy for PMU Placement Considering the Resiliency of Measurement System
Jyoti Paudel, Xufeng Xu, Karthikeyan Balasubramaniam, Elham B. Makram
Electrical and Computer Engineering Department, Clemson University, Clemson, USA

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 October 2015; accepted 17 November 2015; published 20 November 2015
ABSTRACT
This paper aims to find strategic locations for additional Phasor Measurement Units (PMUs) installation while considering resiliency of existing PMU measurement system. A virtual attack agent is modeled based on an optimization framework. The virtual attack agent targets to minimize observability of power system by coordinated attack on a subset of critical PMUs. A planner agent is then introduced which analyzes the attack pattern of virtual attack agent. The goal of the planner agent is to mitigate the vulnerability posed by the virtual attack agent by placing additional PMUs at strategic locations. The ensuing problem is formulated as an optimization problem. The proposed framework is applied on 14, 30, 57 and 118 bus test systems, including a large 2383 node western polish test system to demonstrate the feasibility of proposed approach for large systems.
Keywords:
Observability, Optimization Model, PMU Placement, Resiliency, Scenario Technology, Virtual Attacker

1. Introduction
PMUs play a significant role in wide area monitoring and control. PMUs are capable of measuring node voltages and line currents as phasors. The measured quantities are time stamped based on global positioning satellite (GPS) signal. The time stamp allows analysis of measurement data that is geographically dispersed. Physical properties of power network enable computing the voltage and current phasors across the entire network by installing PMUs at only a subset of nodes.
The PMUs placement in strategic locations has been the vital research topic for PMU application and various methodologies have been introduced by power engineers all across the world [1] . The researchers have approached the PMUs placement problem using two methods: (i) Heuristic approach, (ii) Mathematical approach.
1) Heuristic approaches. They have been widely adopted in this area. Simulated annealing is used in [2] [3] to find the placement location based on desired depth of unobservability. Reference [4] solves the PMU placement problem using recursive Tabu search. Though the algorithm used for this approach gives satisfactory results for larger bus systems but no robust contingency is considered. Literature [5] addresses on N-1 PMU failure and solves the PMU placement problem using differential evolution. Immunity genetic algorithm is used in [6] to investigate the PMU placement. This approach is relatively time consuming and is not preferable for large bus systems. Binary Particle Swam Optimization (PSO) is another optimization approach that is enormously used in this field. In [7] a simple PMU placement has been implemented using BPSO but the algorithm does not consider details regarding PMU vulnerability. Since all the techniques are discussed in heuristic approach, being iterative in nature requires time for convergence and also the convergence fully depends on the initial guess.
2) Mathematical approaches. Mathematical approach has been gaining popularity from recent years. They are easy to apply in the situation where a definite solution is required. They are based on formulae derived from mathematical calculations. Integer linear programming is a common approach as presented in [8] , in which a general formulation for PMU placement using conventional and without conventional measurement is taken into consideration. Contingency constrained optimal PMU placement using exhaustive search approach is proposed in [9] . This literature has taken several zero-injection buses in account for PMU placement considering single PMU loss and measurement channel limitation. Mixed Integer Linear Programming is used in [10] which considers zero injection and branch flow measurements in order to maximize the measurement redundancy and reduce the number of PMUs. However, the approach in [10] requires almost twice the amount of PMUs to obtain full system observability under contingency operation than at normal operating conditions.
Due to the critical nature of power systems, complete observability of all nodes at all times is required. However, the networked PMUs might be rendered out of service by natural disasters such as hurricanes or PMUs can be intentionally taken down by malicious attacks. Enough attention should be given to PMU vulnerability while placing PMUs in the system. The concept of economically deploying PMUs considering resiliency of existing system post attack is missing in the above literatures. Hence, this paper highlights a considerable interest in improving PMU redundancy at minimum cost. In order to ascertain a subset of nodes which are most likely to be attacked, a virtual attack agent is modeled. The aim of the virtual attack agent is to reduce system observability to a minimum while carrying out a coordinated attack on a subset of PMU installation nodes. This virtual attack is used by the operator agent to identify a set of critical nodes whose redundancy needs to be increased. The planner agent then finds strategic locations to place additional PMUs in order to increase redundancy of critical nodes while minimizing incurred cost.
This paper is organized as follows: Section 2 introduces two agents including the attacker and the planner to design a framework for classifying critical PMUs and planning scheme. Section 3 establishes a mathematical model to corporate on their objectives: the attacker aims to disable critical PMUs while the planner tries to design remedial measures. In Section 4, the model is applied to different standard test systems. Finally, Section 5 summaries the paper.
2. Agent Based PMU Placement Framework
An uncertainty constraint PMU placement problem can be expressed in three different agent based stages:
・ Attacker: A virtual attack agent is introduced whose goal is to take down a set of installed PMUs to reduce system observability. Uncertain events like intentional attacks are an important aspect that needs to be considered while making PMU placement decision. Due to geographical span of interconnected power systems planning a coordinated attack on all of the installed PMUs is improbable. Hence, the virtual attack agent will carry out coordinated attacks on a subset of installed PMUs that are deemed critical. Here, the set of critical PMUs are the ones which when taken out of service minimizes system observability. Cardinality of the critical set is assumed to vary depending on the resources available to virtual attack agent.
・ Operator: At this stage, the operator has to take corrective measures to mitigate the possible damage caused by the attacker. The operator agent identifies a set of critical nodes based on virtual attack agents attack plan. The operator agent then relays the corrective measure, which in this case is to increase the redundancy of critical nodes, to the planner agent.
・ Planner: The task of planner is to deploy additional PMUs to increase redundancy of critical nodes at minimum cost.
Schematic representation of the three cyclic stages is shown in Figure 1. The schematic is cyclic in nature because of the nature of the problem, where the virtual attack agent comes up with strategies to minimize system observability given a set of PMU locations. The operator and planner agents then mitigate the effect of virtual attack agent by placing additional PMUs at strategic locations. The virtual attack agent then starts a new cycle with the new set of PMU installation locations.
Each undesired PMU outage caused by the virtual attack agent is an optimization scenario for the operator. These undesired outages can be single, double or multiple based on virtual attack agent’s resources. Let P be the number of PMUs deployed into the system and Ψ be the scenario which corresponds to the number PMUs to be attacked by the attacker. The total scenario can be represented as combinatorial number PCΨ as:
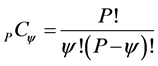 (1)
(1)
Since there are hundreds of thousands of possible attack scenarios, it is impossible to enumerate all scenarios for large systems due to computational burden. Instead, by adopting the approach in (2) a worst case scenario can be obtained.
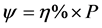 (2)
(2)
where ƞ Î [0, 100]―representing the percentage of installed PMUs that are attacked. As a worst-case scenario, an assumption has been made that the attacker can attack up to 50% of the total deployed PMUs. Depending upon ƞ value, a set of attacked PMUs 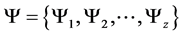 is obtained from the optimization problem and this set is named as critical PMUs. The programming framework for the agent based PMU placement is shown in Figure 2.
is obtained from the optimization problem and this set is named as critical PMUs. The programming framework for the agent based PMU placement is shown in Figure 2.
Figure 1. Relationship between three agents in PMU placement.
Figure 2. PMU placement framework.
3. Mathematical Formulation
Development of agent models as an optimization problem is discussed in this section. The initial deployment locations for PMUs, which act as the starting point for the proposed agent based framework are obtained using optimal PMU placement algorithm from [8] .
3.1. Virtual Attack Agent
The objective of virtual attack agent is to attack a subset of installed PMUs in the system such that the system bus observability is minimized. The attack agent is modeled using binary integer programming.
The mathematical formulations for attacker’s objective is as follows:
 (3)
(3)
S.t.
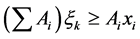 (4)
(4)
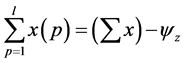 (5)
(5)
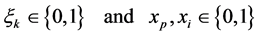 (6)
(6)
The objective function (3) ξk is the decision variable that tends to give the observability of each bus in terms of binary variable. If the bus is observable by PMUs remaining in the system after the coordinated attack by virtual attack agent then ξk will take the value of 1 and if the bus is not observable by any of the PMUs then ξk will take the value ‘0’. In general, observability of a bus can be 0 in which case the bus is not observable or observability can be a positive number which means the bus is observable.
 (7)
(7)
Since the available PMUs were placed based on system network topology, it becomes necessary to define a network connectivity matrix A.
Elements in matrix A are defined as follows:
 (8)
(8)
In constraint (4), xi is an auxiliary binary variable of PMU placement. If the PMU is present at the ith bus then xi is regarded as 1 otherwise 0. Before the attack, the observability of the ith bus denoted by left-hand side of (4) should be equal to the product of connectivity matrix of bus i and PMU placement variable xi. Since the attacker already know the exact location of the PMUs, the attacker agent tries to enumerate all the possibilities to destroy or damage the PMU which are critical. This procedure is presented in (5). The word ‘critical’ defines those set of PMUs whose installation in the system increases the system observability. Post attack the variable xi is zero for the disabled or attacked PMU. In this case, the constraint (4) will act as inequality constraint because the observability of the bus at right hand side will be greater than left hand side. The connectivity matrix is always fixed as long as all the transmission lines in the system are in service. The variable xp is the PMU placement variable post attack. Depending upon the auxiliary variable xp, the attacker performs all combinatorial number and checks the observability of each bus one by one. Those combination sets where the observability of bus shows the maximum number, the attacker tries to attack on those particular sets of PMUs. Constraint (4) helps the attacker to judge the most attractive set of PMUs to act on.
Computational complexity of this optimization model increases substantially when dealing with large number of system buses. From (4), the total number of inequality constraints is equal to the number of system buses N and the equality constraint (5) is split into two sections, one for the set of the buses where PMUs were installed and other for the set of buses where PMUs were not installed. Therefore the total number of constraints is N + 1 + 1. Similarly the total numbers of variables are twice the number of system buses M. This is because the first half M/2 denotes the auxiliary variable of PMU placement post attack and the other half M/2 denotes the bus observability.
3.2. Operator Agent
The responsibility of the operator is to identify vulnerable nodes based on the behavior of virtual attack agent. Vulnerable nodes in this context are a set of critical buses whose observability is compromised by the virtual attack agent. Critical buses are the buses include critical PMU installation buses and buses that are observable by critical PMUs.
The number of PMUs attacked by virtual attack agent is a percentage of the total number of installed PMUs. Since, larger systems have larger number of installed PMUs, the number of critical buses also tends to increase with system size. Since various sets of PMUs were obtained depending upon the availability of attacker’s resources. Now, with the concern of PMU’s and their installation cost, from those several sets of classified critical PMUs, the planner has to choose only the most repeated PMUs among all sets of critical PMUs. To obtain this, following formulation is used.
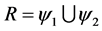 (9)
(9)
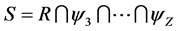 (10)
(10)
where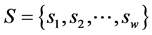 , denotes set of critical PMUs in (10).
, denotes set of critical PMUs in (10).
The critical buses are those buses that are observable from the set of critical PMUs.
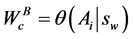 (11)
(11)

where 
3.3. Planner Agent
The objective of the planner agent is to install additional PMUs in strategic locations to mitigate the vulnerability posed by virtual attack agent. The optimal PMU placement considering the critical PMUs is as follows:

Subject to





The objective function (13) implies that minimum number of PMU is placed in the system and 



4. Discussion and Result
The performance of proposed model is tested on 14, 30, 57 and 118 IEEE test bus systems including large power system 2383 bus Western Polish system [11] [12] . All the testified cases are implemented on 1.70 GHz processor with 6 GB of RAM using CPLEX12.6.2 Solver [13] . The optimization is executed in MATLAB environment.
4.1. Critical PMUs
The number of critical PMUs depends upon the size of the system and the system topology. The set of PMUs that poses a higher influence in increasing the system bus observability are shown in the Table 1. The critical PMUs are obtained based upon the resources available to the attacker. The percentage shown in the Table 1 indicates that the attacker has ability to damage certain percentage of the total deployed PMUs in the system. For a small system like14 bus system, only 4 PMUs are needed in the system for full observability before attack. 10% of 4 PMUs being a negligible number, 20% and 50% of total placed PMUs is considered for execution. Nmin is the number of attacked PMUs. Similarly, Table 1 demonstrates all the critical PMUs for different IEEE systems.
To further analyze strictly critical PMUs, only one set of PMUs per system is evaluated. The PMUs that happens to be critical for more than twice among the differentiated level of resources availability are only considered as most critical PMUs. Figure 3 shows all such single set of most critical PMUs for 14, 30, 57 and 118 IEEE bus systems only. The model was further tested for larger power systems like IEEE 300 and 2383 Western Polish system. For the larger system, the most critical PMU buses are shown in Table II. The critical PMUs for larger systems are selected based on 10% of total installed PMUs. Since the numbers of PMUs installed in IEEE 300 and 2383 Western Polish system outnumbered to smaller system, PMU installed buses are not shown in the described Table 2.
4.2. Planning Scheme for PMU Placement
The PMU placement planning scheme is presented in this section. The goal of the planning scheme is to place additional PMUs in order to mitigate the loss of observability in the event of an attack. From the previous section, the set of critical buses with respect to loss of observability was obtained. The planner agent uses this
Figure 3. Critical PMUs in different test systems.
information to obtain PMU placement scheme for installing additional PMUs with least cost to increase redundancy of critical nodes. For the most critical buses as shown in Table 3, the measurement redundancy was set to 2 i.e. the most critical buses must be observable by at least 2 PMUs. The resultant optimal numbers of PMUs are shown in Table 4. For IEEE 14 bus system, two additional PMUs are required to increase redundancy of five critical buses. Similarly for IEEE 30 bus system four additional PMUs are required to increase redundancy of 12 critical buses. Since the original PMU deployment was shown in Table 1, Table 4 shows PMU locations only for additional PMUs. Due to space limitation, location of additional PMUs for larger systems are not tabulated but are rather summarized as follows. For IEEE 300 bus system, 30 additional PMUs are required. While the 2383 bus polish system required 252 PMUs in addition to the originally placed 746 PMUs to obtain full bus system observability and increased redundancy at critical buses.
Table 1. Critical PMUs depending upon IEEE test systems.
Table 2. Critical buses with PMUs on Larger systems.
Table 3. Critical buses for different test systems.
Table 4. Comparison of No. of Optimal PMUs under normal condition and uncertainty events.
5. Conclusion
This paper proposes a planning approach for optimal PMU placement making the system more resilient to PMU failure. The likelihood of undesired events is analyzed by creating a virtual attack agent which intends to damage some of the critical PMUs in the system. Operator agent is used to obtain a subset of buses that are critical based on the attack pattern of virtual attack agent. Simulation results illustrate the ability of the planner agent to place additional PMUs at strategic locations to increase the redundancy of critical buses. The developed framework was tested on several test systems including a 2383 bus western polish system and optimal results were obtained in all cases. Future work will consider the account of zero-injection measurement and branch flow measurement for more economical solution.
Cite this paper
Jyoti Paudel,Xufeng Xu,Karthikeyan Balasubramaniam,Elham B. Makram, (2015) A Strategy for PMU Placement Considering the Resiliency of Measurement System. Journal of Power and Energy Engineering,03,29-36. doi: 10.4236/jpee.2015.311003
References
- 1. Manousakis, N.M., Korres, G.N. and Georgilakis, P.S. (2012) Taxonomy of PMU Placement Methodologies. IEEE Transactions on Power Systems, 27, 1070-1077.
http://dx.doi.org/10.1109/TPWRS.2011.2179816 - 2. Zhang, J., Welch, G., Bishop, G. and Huang, Z. (2010) Optimal PMU Placement Evaluation for Power System Dynamic State Estimation. IEEE PES, Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenburg, 11-13 October 2010, 1-7.
- 3. Nuqui, R.F. and Phadke, A.G. (2005) Phasor Measurement Unit Placement Techniques for Complete and Incomplete Observability. IEEE Transactions on Power Delivery, 20, 2381-2388.
http://dx.doi.org/10.1109/TPWRD.2005.855457 - 4. Koutsoukis, N.C., Manousakis, N.M., Georgilakis, P.S. and Korres, G.N. (2013) Numerical Observability Method for Optimal Phasor Measurement Units Placement Using Recursive Tabu Search Method. IET Generation, Transmission & Distribution, 7, 347-356.
http://dx.doi.org/10.1049/iet-gtd.2012.0377 - 5. Peng, C., Sun, H. and Guo, J. (2010) Multi-Objective Optimal PMU Placement Using a Non-Dominated Sorting Differential Evolution Algorithm. International Journal of Electrical Power & Energy Systems, 32, 886-892.
http://dx.doi.org/10.1016/j.ijepes.2010.01.024 - 6. Aminifar, F., Lucas, C., Khodaei, A. and Fotuhi-Firuzabad, M. (2009) Optimal Placement of Phasor Measurement Units Using Immunity Genetic Algorithm. IEEE Transactions on Power Delivery, 24, 1014-1020.
http://dx.doi.org/10.1109/TPWRD.2009.2014030 - 7. Peppanen, J.,Alquthami, T., Molina, D. and Harley, R. (2012) Optimal PMU Placement with Binary PSO. IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, 15-20 September 2012, 1475-1482.
- 8. Gou, B. (2008) Generalized Integer Linear Programming Formulation for Optimal PMU Placement. IEEE Transactions on Power Systems, 23, 1099-1104.
http://dx.doi.org/10.1109/TPWRS.2008.926475 - 9. Azizi, S., Dobakhshari, A.S., Nezam Sarmadi, S.A. and Ranjbar, A.M. (2012) Optimal PMU Placement by an Equivalent Linear Formulation for Exhaustive Search. IEEE Transactions on Smart Grid, 3, 174-182.
http://dx.doi.org/10.1109/TSG.2011.2167163 - 10. Esmaili, M., Gharani, K. and Shayanfar, H.A. (2013) Redundant Observability PMU Placement in the Presence of Flow Measurements Considering Contingencies. IEEE Transactions on Power Systems, 28, 3765-3773.
- 11. Christie, R. (1993) Power System Test Archive.
https://www.ee.washington.edu/research/pstca - 12. MatPower.
http://www.pserc.cornell.edu//matpower/ - 13. The ILOG CPLEX Website, 2015.
http://www.ilog.com/products/cplex





