Received 15 June 2016; accepted 21 June 2016; published 26 July 2016

ABSTRACT

Managers of cement plants are gradually becoming aware of the need for soft sensors in product quality assessment. Cement clinker quality parameters are mostly measured by offline laboratory analysis or by the use of online analyzers. The measurement delay and cost, associated with these methods, are a concern in the cement industry. In this study, a regression-based model was developed to predict the clinker quality parameters as a function of the raw meal quality and the kiln operating variables. This model has mean squared error, coefficient of determination, worst case relative error and variance account for (in external data) given as 8.96 × 10⁻⁷, 0.9999, 2.17% and above 97%, respectively. Thus, it is concluded that the developed model can provide real time estimates of the clinker quality parameters and capture wider ranges of real plant operating conditions from first principle-based cement rotary kiln models. Also, the model developed can be utilized online as soft sensor since they contain only variables that are easily measured online.

Keywords:

Clinker Quality Parameters, Online Estimation, Cement Rotary Kiln, Model, Soft Sensor

1. Introduction

Cement plays an important role in the construction industry. It is the principal hydraulic binder, and the major strength-giving and property-controlling component of concrete. The raw materials for cement production are usually quarried from local rocks, crushed, and then heated at temperature in excess of 1000˚C in a rotary kiln to form clinker. The quality of the clinker determines the property (such as compressive strength) of the cement made from it; the basis for this property is reported to be the result of a well-burned clinker with consistent chemical composition and free lime [1] . Keeping the quality of the clinker within acceptable range requires that measurement of the quality parameters be done from time to time in the laboratory, or using online hardware sensors which are based on X-ray fluorescence (XRF) and X-ray diffraction (XRD) techniques. The clinker quality parameters are Lime Saturation Factor (LSF), Silica Moduli (SM), Alumina Moduli (AM), dicalcium silicate or belite (C₂S) concentration, tricalcium silicate or alite (C₃S) concentration, tricalcium aluminate (C₃A) concentration, and tetracalcium aluminoferrite (C₄AF) concentration [2] [3] . The time delay associated with determining these parameters in the laboratory or with online hardware sensors using XRF techniques are about four hours and around fifteen minutes, respectively [3] . As a result of the measurement delay, any reduction in the clinker quality results in outright rejection or recycling of the formed clinker [2] . For better product quality, and online estimation of the quality parameters in real time, soft sensor is considered as a more attractive option in comparison with online hardware sensors. Quite a few works have been reported on the application of soft sensors to the cement industries. The soft sensors developed have all been data driven, such as, neural network based soft sensors [2] [3] ; multivariate statistical based soft sensor [4] and Support Vector Regression (SVR) based soft sensor [5] for online estimation of product quality in cement plant. However, the challenge with these models is that their accuracy depends largely on the quality of the historical data obtained from the rotary kiln. Moses and Alabi [6] reported that experiments can be performed on the real plant to capture wider ranges of operating conditions, but Plant Managers rarely will allow deliberate changes to the operating conditions of the plant. Hence, one cannot extrapolate beyond the boundaries for which these soft sensor models were developed.

To deal with the challenges accompanying the data-driven soft sensors, First Principle Models (FPMs) can be applied. Although several FPMs have been developed for optimization and control of cement rotary kilns, none has been developed for soft sensing of cement clinker quality parameters. First principle models have the advantages of being able to capture the physicochemical behaviour of the rotary kiln and have good extrapolation property. Unfortunately, the existing first principle-based rotary kiln models contain variables that are difficult to measure real time, and also are a system of nonlinear Differential-Algebraic Equations (DAEs) which must be solved numerically. Hence, these FPMs are not in the form suitable for online implementation as soft sensors and so, cannot be applied online in their current forms. Therefore, in this work, a framework was developed for converting the first principle models of cement rotary kiln available in the literature to the form useful for online estimation of cement clinker quality parameters. Soft sensor is needed for online sensing of the clinker compositions coming out of the cement rotary kiln because it can also function as a backup sensor when the hardware sensor (using XRF and/or XRD techniques) is faulty or down for maintenance or replacement [3] . Therefore, this study is focused on the development of a regression-based model for online estimation of clinker quality parameters. The developed model is in the form that can be directly utilized as soft sensors (in clinker production unit of the cement manufacturing plant) as opposed to the existing theoretical and semi-empirical models. Also, the models were developed from (range of) operating conditions that are wider than the typical operating conditions of a real plant. Thus, this model is expected to perform well in an environment where the existing empirical models will fail (for lack of extrapolation ability). Hence, with this framework, real time estimation of clinker quality parameters for cement production can be achieved.

2. Methodology

In the cement manufacturing process, the quality of the clinker exiting the rotary kiln determines the eventual quality of the cement produced. In this study, regression models were developed for online estimation of the clinker quality parameters. Experimental designs were performed to investigate the effect of the process (input) parameters on the clinker quality parameters. Numerical solution of first principle and semi-empirical based cement rotary kiln models was obtained at different operating conditions and the data obtained were used to develop the regression models for online estimation of clinker quality parameters.

Real life data from cement plants are not easily available because, for cement manufacturing companies to gain competitive advantage, they keep their data and experience confidential [7] . Even if these data are available, they only capture the normal operating conditions of the plant. Models built with these types of data can only be valid within the range of the normal operating conditions. To capture wider operating conditions of the plant (should there be changes in process characteristics), experimentation on the real plant will be required. However, Plant Managers rarely will allow deliberate changes to the operating conditions of their plants. This is no doubt that the reason simulation approach was employed in this study. However, the choice was guided by the goal of measurement of clinker quality parameters which is to provide reliable, real-time and online measurement of the clinker quality parameters. The fundamental and semi-empirical models for cement rotary kiln used in this study are those that have been validated using real plant data; hence, the data (solutions) are deemed reliable as they capture the physicochemical behaviour of the process. Therefore, the regression models developed will not only retain the accuracy of the first principle and semi-empirical models they were developed from but are in the form suitable for online application in view of the fact that the input parameters are easily measured online.

2.1. Model Formulation

The model for cement rotary kiln (Equations (1)-(14)) used in this study is a collation from the works of Darabi [7] , Mastorakos and Co-workers [8] , Zhuo and Co-workers [9] and Sadighi and Co-workers [10] . This model, a system of twelve differential-algebraic equations and two algebraic equations, involves appropriate mass balance (normalized with respect to the mass of CaO), energy balance and material residence time for the axial evolution of the components involved in the clinker formation, temperature profiles and the movement of solids within the kiln respectively.

2.1.1. Steady State Material Balance Equations

The equations that describe the one-dimensional steady-state axial evolution of components involved in the clinker formation are given as Equations (1)-(9) [7] - [9] .

Calcium Carbonate (Lime Stone)

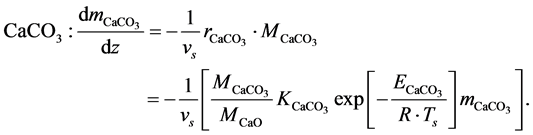(1)

Calcium Oxide (Quick lime)

(2)

Silicon (IV) Oxide (Silica)

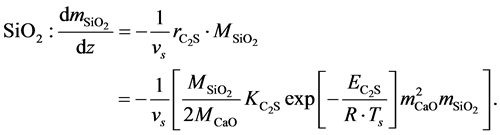(3)

Aluminum Oxide (Alumina)

(4)

Iron (III) Oxide

(5)

Dicalcium Silicate (Belite)

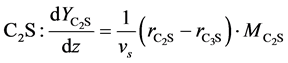
(6)

Tricalcium Silicate (Alite)

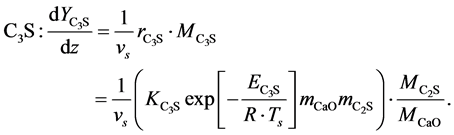(7)

Tricalcium Aluminate (C₃A)

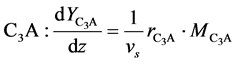
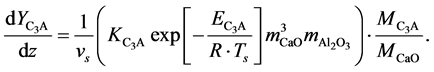(8)

Tetracalcium Aluminoferrite (C₄AF)

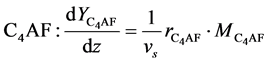
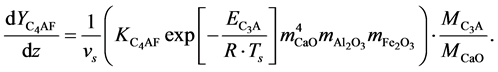(9)

2.1.2. Steady State Energy Balance Equations

The energy balance equations that describe the one-dimensional steady-state axial temperature profiles of the phases involved in clinker formation are given as Equations (10)-(12) [10] .

Gas (Free Board) Phase

(10)

Solid (Bed) Phase:

(11)

Wall Phase

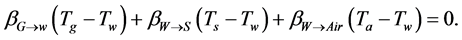(12)

The residence time and velocity of the solid materials within the rotary kiln are described by Equation (13) Equation (14) [9] .

Velocity of the solid,

(13)

Material residence time,

(14)

where, the heat transfer coefficients (), heat released by fuel combustion (), enthalpy of the chemicals () and other parameters where obtained from [7] [8] [10] .

2.2. Numerical Solutions of the Fundamental and Semi-Empirical Models

The twelve differential-algebraic equations (DAEs) in section 2.1 (from which the regression model was developed) are not in the form suitable for soft sensing of clinker quality parameters. To transform this model to a form suitable for soft sensing of clinker quality parameters, numerical solutions are required.

Mastorakos and Co-workers [8] , Lu and Co-workers [11] , Darabi [7] , Akhtar and Co-workers [12] and Bhad and Co-workers [13] all developed computational fluid dynamics (CFD)-based models to simulate cement rotary kiln. However, the simulation approach they employed was not an applicable method for estimation of clinker quality parameters because of the considerable calculation time required to determine the kiln wall temperature. Therefore, to circumvent this challenge, this study employed explicit Euler’s algorithm for a system of DAEs on the platform of Microsoft Excel spreadsheet.

Furthermore, to verify the simulation approach adopted in this work, the operating conditions of a typical industrial plant obtained from [8] were plugged into the simulation (solution) platform. The simulation reproduced the result obtained in the work of Mastorakos and Co-workers [8] to an accuracy of 4.11% (worst case relative error). Hence, the data (solutions) are deemed reliable as they capture the physicochemical behaviour of the cement rotary kiln adequately.

2.3. Experimental Design for the Estimation of Cement Clinker Quality Parameters

Having verified the simulation approach adopted in this study, data in the range of the plant’s operating conditions and the values of some process parameters for a typical cement manufacturing plant were obtained from [8] [10] [14] . The operating conditions used for the simulation are as shown in Table 1.

With these operating conditions, a central composite response surface design (with 1/2 fraction) was used to generate one hundred and fifty-four (154) data points. These data points were then plugged into the rotary kiln simulation platform to determine the response variables for a combination of the inputs/factors. Furthermore, with the aid of Design Expert 7.0 statistical tool, these 154 data points were then used (after outlying data points had been removed based on the method described in section 2.3.1) to build the regression models.

Outlier Detection

An outlier is defined as an observation that “appears” to be inconsistent with other observations in the data set [15] . It is important to detect and delete outliers because they may lead to model misspecification, biased parameter estimation and incorrect analysis result [11] . There are various approaches to outlier detection. One of

such approach is, visual inspection. Although visual inspection alone cannot always identify an outlier and can lead to mislabeling an observation as an outlier. Pani and Co-workers [2] reported that, whenever it is not possible to apply visual inspection, the three popular outlier techniques: 3δ edit rule, the Box plot method and Hampel’s method can be used to detect outliers.

In this study, 3δ edit and the Box plot methods were applied to each of the operating (response) variable data set. For the 3δ edit rule, a data set was labeled outlier when the data points were three or more standard deviations from the mean. That is,

(15)

While, the Box plot method defines regions (upper and lower fences) in the plot beyond which a data set may be labelled an outlier. These regions are:

(16)

and are 25 and 75 percentiles respectively. A mild outlier is a point beyond an inner fence on either side while an extreme outlier is a point beyond an outlier fence.

Furthermore, the Externally Studentized Residual (ESR) diagnostic platform, of central composite design (CCD in) Design Expert 7.0 software was used to detect and eliminate outliers because it uses the concept of 3δ edit rule, and also handled outliers in all five responses simultaneously contrary to the box-plot method.

2.4. Error Propagation/Uncertainty Associated with the Data Collected from the Simulation

Any numerical method that computes an approximate solution, is usually accompanied with some limitations, especially its error. Thus, the uncertainty surrounding the data from which the regression models were built is a function of the error propagation in the numerical technique employed. This error propagation is reported in [16] as:

(17)

where; m is composition (mass fraction); is the kiln length at step n.

Alternatively, according to Söderlind and Arévalo [17] , if the global error recursion in Equation (17) and norms are taken with Lipschitz condition applied, we have Equation (18).

(18)

(19)

This numerical approach converges because

(20)

Hence to minimize this error, a very small step size was used for the simulation in this study; though it resulted in a longer computational time.

2.5. Mathematical Relations for Calculating Cement Clinker Quality Parameters

In the chemical analysis of cement, certain mathematical relations exist between the percentage of lime and the combination of compounds like silica, alumina and iron oxide [1] [18] . These relations are:

2.5.1. Lime Saturation Factor

Lime saturation factor (LSF) which is the ratio of the actual amount of lime to the theoretical lime required by the other major oxides in the clinker was calculated using the Equation (21).

(21)

2.5.2. Silica Moduli

Silica Moduli (SM) which gives an idea of the amount of melt phase present in the burning zone of the kiln was calculated from the formula given in Equation (22):

(22)

2.5.3. Alumina Moduli

The Alumina Moduli (AM) which determines the composition of liquid phase in the clinker was calculated from the formula given in Equation (23):

(23)

2.5.4. Alite and Free Lime

These quality parameters did not require formulae for their determination. For instance, free lime (FCaO) is simply the amount of unreacted lime free in the clinker; Alite (C₃S) was among the kiln exit compositions.

2.6. Regression Model(s) Development

The regression models (eight (8) input-five (5) response model) were built following the steps (below) in Design Expert 7.0 statistical software.

・ The values of the responses (for each design run) in the simulation platform were copied into the central composite design layout view of the Design Expert software.

・ Each response variable was transformed for cases where the ratio of maximum to minimum response value was above 10. Otherwise, transformation was not necessary.

・ The fit summary environment was viewed to access information about the goodness of fit of the model (such as degree of freedom, F-value, P-value) and the model summary statistics (such as standard deviation, , PRESS). Also, it gives information on which model is aliased. With F-test, one can know if a group of variables are jointly significant. P-value, which must be less than the alpha level is the probability that the results have happened by chance. Predicted Residual Error Sum of Squares (PRESS) statistic estimates how the model performs on hold-out data, using only in-sample data [19] .

・ Backward elimination regression (with alpha = 0.05) was employed at model process order (which could be linear, 2FI, quadratic, cubic) for automatic elimination of undesired model terms.

・ Analysis of variance (ANOVA) platform which analyzes the chosen model gave a view of the results of analysis.

・ Diagnostic platform which evaluates the model fit and transformation choice with graphs (such as normal plot, residual vs prediction, etc.) was viewed to make a final choice on the model type.

Finally, the coefficients of the proposed regression model given in Equation (24) were determined from ANOVA using Design Expert 7.0 software.

(24)

where R is the estimated response variable (clinker quality parameters, i.e., LSF, SM, AM, etc.); are the input parameters (CaO, SiO₂, Al₂O₃, Fe₂O₃, mass flow rate of solid, feed inlet temperature, mass flow rate of fuel and mass flow rate of air); represents the mean (intercept); are the linear effects; are the quadratic effects while are the interaction effects.

2.7. Performance Evaluation of the Developed Regression Models

Two sets of data (interpolation and extrapolation) were obtained through two (2)-level factorial design (Res IV) to evaluate the performance of the model.

2.7.1. Interpolation Test

New operating conditions for the interpolation test were created and plugged into the simulation platform of the first principle-based rotary kiln model to generate response data for the interpolation test. The lower boundary (LB) of the new operating conditions was 110% LB of the (original) operating conditions used to develop the model while the upper boundary (UB) was 90% UB of the (original) operating conditions. The response data so generated were compared with the model predictions at the same design points.

2.7.2. Extrapolation Test

For the extrapolation test, the lower boundary (LB) of the new operating conditions was 90% LB of the (original) operating conditions that were used to develop the model while the upper boundary (UB) was 110% UB of the (original) operating conditions. These response data were compared with the model predictions at the same design points.

2.8. Other Performance Criteria for the Developed Regression Models

In addition to the statistical criteria outlined in section 2.6, the performance of the model developed in this study was determined by evaluating the percent relative error, coefficient of determination (R²) and the mean of squared error (MSE) values produced by each model to the trained data (i.e. data used to build the model) and untrained data (i.e. data different from the model data). The Equations (25)-(27) were used to calculate the above mentioned performance criteria.

(25)

where, , is the predicted value of the independent variable and y is the simulated value.

(26)

(27)

Furthermore, analysis of the estimation capability of the developed model was done by computing the variance account for (VAF) values of the model for the unknown (external) data. The VAF values of the model used for predicting the clinker quality parameters were calculated in Microsoft Excel using Equation (28) [2] .

(28)

The performance criteria are:

・ Statistically, a good model will have [20] [21] .

・ The closer the VAF value is to 100%, the better the model prediction capability [2] .

3. Results and Discussions

3.1. Regression Model for Estimation of Clinker Quality Parameters

Response surface model was used to fit the first principle-based cement rotary kiln simulation data generated in this study. The model developed is a second order regression model, presented as Equation (29).

(29a)

(29b)

where

(29c)

where

(29d)

(29e)

where

The regression model (29) is a relationship between the clinker quality parameters and the input variables: CaO (A), SiO₂ (B), Fe₂O₃ (C), Al₂O₃ (D), mass flow rate of solid (E), feed inlet temperature (F), mass flow rate of fuel (G) and mass flow rate of air (H).

3.2. Estimation of the Capability of the Developed Model

Figure 1 gives the estimation capability of the developed model presented in section 2.6 with respect to the trained data. Also, Table 2 shows the minimum MSE and worst case relative error achieved for the models.

The performance of the developed regression model was evaluated by comparing its predictions with the simulated first principle-based cement rotary kiln model under the same input conditions. Moreover, some statistical criteria presented in section (2.10) were used to evaluate the capability of the regression model. The results are as reported in Figure 1. Table 2 shows that, the model developed in this work fits the data well with minimum MSE of 8.96E−07 and worst case relative error of 2.17%. With the model accounting for about 99% variation in the data, the model can be used for estimation of the clinker quality parameters.

3.3. Performance Evaluation of the Developed Models

The estimation capabilities of the developed regression model were evaluated with respect to untrained data obtained from simulation (with 2-factor design interpolation data and extrapolation data) as described in section 2.7.

3.3.1. Interpolation Test of the Developed Models

Figure 2 shows the estimation capability of the regression model with respect to the interpolation data. Also, Table 3 shows the variance account for (VAF) of the model in predicting the clinker quality parameters.

The interpolation capability of the regression model was tested by evaluating its predictive ability using a set of simulated data different from the ones used to develop the model. The results are as reported in Figure 2. From the figures, it is obvious that, the model performs well in response to operating conditions different from (but within the range of) operating conditions used for building it. Furthermore, with the variance accounted for (VAF) statistical criterion, Table 3 reveals that, the model (with VAF values closer to 100) has high estimation capability. Thus, the model is both accurate and generally adequate for the purpose of predicting clinker quality parameters under different operating conditions.

3.3.2. Extrapolation of the Developed Models

Figure 3 shows the estimation capability of the developed regression model with respect to the extrapolation data. Also, Table 4 shows the variance account for (VAF) of the model in predicting the clinker quality parameters for extrapolation (input) data.

The extrapolation capacity of the regression model was tested by evaluating its predictive ability using a set of data outside the population of simulation data used to develop the model. The results are as reported in Figure 3. From the figures, the model performs well in response to operating conditions outside the range of operating conditions used to build it. The variance accounted for (VAF) statistical criterion, further reveals that (Table 4), the model has high estimation capability. Furthermore, Table 4 shows that, for 10% deviation (extrapolation data generated from 110% upper boundary and 90% lower boundary of the plant’s normal operating conditions)

outside the plant’s normal operating conditions the model can handle worst case relative error less than 20%. Practically, this error is reasonable as a 10% deviation may result in out-of-specification production.

The estimation capability of the model is satisfactory having met the performance criteria of a predictive model. Therefore, it can be used for online estimation of clinker quality parameters. In addition, this model produces result real time when the input variables are provided, unlike the theoretical model which requires the investigator to wait for its numerical solution to converge. Hence, it can be concluded that the model has the potential to meet the challenge of (real-time) online measurement of clinker quality parameters, by providing reliable, fast online estimation of clinker quality parameters for high quality cement production.

4. Conclusions

Online, accurate estimates of clinker quality (in real time) will eliminate additional energy and production cost associated with out-of-specification production. Unfortunately, soft sensors developed in the literature for clinker quality parameters are data driven and custom built. So, if the operating conditions of the plant drift away from the original operating range from which the model was built, a new model must be redeveloped.

In this study, a regression-based model was developed for online prediction of clinker quality parameters. The developed model can provide the plant operators with information on clinker quality, for quick control actions which will eventually lead to product quality improvement. The estimation capability of the developed model was satisfactory based on the statistical criteria: mean squared error, coefficient of determination, worst case relative error and variance account for (in external data) given as 8.96 × 10⁻⁷, 0.9999, 2.17% and above 97% respectively. Also, the developed model is robust as it captures wider ranges (within and outside) of the real plant operating conditions. Hence, the developed model can be utilized as soft sensor since it contains only variables that are easily measurable online.

It is recommended (for further study) to use nonlinear techniques to develop models from the first principle- based cement rotary kiln simulation data (solutions).

Cite this paper

Nsidibe-Obong Ekpe Moses,Sunday Boladale Alabi, (2016) Predictive Model for Cement Clinker Quality Parameters. Journal of Materials Science and Chemical Engineering,04,84-100. doi: 10.4236/msce.2016.47012

References

NOTES

^*Corresponding author.