Received 4 August 2015; accepted 5 September 2015; published 8 September 2015

ABSTRACT

Synthetic zeolite Na-A was prepared from Egyptian kaolinite by hydrothermal treatment to be used as an adsorbent for removal of phosphate from aqueous solutions. The present work deals with the application of response surface methodology (RSM) and central composite rotatable design (CCRD) for modeling and optimization of the effect of four operating variables on the removal of phosphate from aqueous solution using zeolite Na-A. The parameters were contact time (0.5 - 6 h), phosphate anion concentrations (10 - 30 mg/L), adsorbent dosage (0.05 - 0.1 g), and solution pH (2 - 7). A total of 26 tests were conducted using the synthetic zeolite Na-A according to the conditions predicted by the statistical design. In order to optimize removal of phosphate by synthetic zeolite Na-A, mathematical equations of quadratic polynomial model were derived from Design Expert Software (Version 6.0.5). Such equations are second-order response functions which re- present the amount of phosphate adsorbed (mg/g) and the removal efficiency (%) and are expressed as functions of the selected operating parameters. Predicted values were found to be in good agreement and correlation with experimental results (R² values of 0.918 and 0.905 for amount of phosphate adsorbed and removal efficiency of it, respectively). To understand the effect of the four variables for optimal removal of phosphate using zeolite Na-A, the models were presented as cube and 3-D response surface graphs. RSM and CCRD could efficiently be applied for the modeling of removing of phosphate from aqueous solution using zeolite Na-A and it is efficient way for obtaining information in a short time and with the fewer number of experiments.

Keywords:

Zeolite Na-A, Hydrothermal, Phosphate, Optimization

1. Introduction

Wastewater is one of the biggest environmental problems all over the world [1] . It is usually hazardous to human populations and the environment and it is critical to be treated prior to disposal into streams, lakes, seas, and land surfaces [2] . Surface waters contain certain level of phosphorus (P) in various compounds, which is an important constituent of living organisms [1] . Phosphorus (P) is a major limiting nutrient for the growth of phytoplankton including cyanobacteria causing eutrophication [3] [4] .

Increasing the phosphorous concentration resulted in impairing the water quality and causing many problems as cloudy lakes, depletion of oxygen in deep water in lakes, high purification costs, decreased recreational and conservation value of water bodies, loss of livestock and the possible lethal effect of algal toxins on drinking water [5] . Controlling phosphorous pollutions is critical for agriculture environmental protection and water environment quality development [6] - [8] .

There are several methods which have been applied to eliminate phosphorous in waste water including chemical precipitation, biological removal, crystallization, adsorption and ion exchange [9] - [11] . Phosphorus adsorption is the main technology for phosphorus co-precipitation; the process involves adsorption of phosphorus onto the surface of the co-precipitant, followed by a slow incorporation of phosphorus into the structure of the adsorp- tive material to scavenge phosphorus from the water [12] . Co-precipitant materials for phosphate removal include limestone, gypsum, fly ash and natural calcite [13] [14] , but such material has low adsorption capacities [4] - [15] .

Zeolite molecular sieves are crystalline microporousaluminosilicates with an indefinitely extending three- dimensional network of AlO₄ and SiO₄ tetrahedrons linked by sharing of oxygen atoms [16] . Zeolite minerals are characterized by high surface area, rigid three-dimensional structures free of swelling behavior and high cation exchange capacity [17] ; therefore, zeolites exhibit amazing sorption and hydraulic properties and commonly used in waste water remediation [18] .

Zeolites are usually synthesized under hydrothermal conditions from basic aluminosilicate precursor gels at elevated temperatures [19] [20] . Zeolites were synthesized using different materials such as carbonized rice husk [21] , low-grade natural kaolin [22] , natural and modified diatomite [16] , kaolinite [23] , rice husk [24] , rice husk ash and metakaolin [25] , fly ash [26] , paper sludge ash [27] , chrysotile and rice husk [28] and rectorite mineral [29] . The A-type zeolite is one of the most common synthetic zeolites which have various applications in industry as catalysis, separation, ion exchange and adsorption [30] (Xing-dong et al., 2013). Synthetic zeolites can be used as adsorbents or substitute for sodium tri-polyphosphate [31] [32] .

The aim of this paper focuses on applying, response surface methodology (RSM) and statistical Central Composite Rotatable Design (CCRD) to evaluate the interactive effect of the selected factors and to obtain the optimum conditions for maximum removal of phosphate from aqueous solution by synthetic zeolite Na-A from Egyptian kaolinite.

2. Statistical Experimental Design

2.1. Response Surface Methodology (RSM)

Response Surface Methodology (RSM) is a collection of mathematical and statistical techniques used in significance of several affecting factors in an optimum manner, even in the presence of complex interactions [33] . The main reason for implementing RSM is to determine the optimum operational conditions for the process or to determine a region that satisfies the operating specifications [34] . Response Surface Methodology (RSM) attracted the attention of many researchers as a result of its advantages in reducing the number of experiments, understanding the pattern in which the measured response is affected by any changes in the selected variables [35] . The main advantage of RSM is that it enables the improvement of the product from predicted property values and its ability to predict the interactions of more than two or more factors (interactive effects) and effects due to collective contributions of the measured response. If the selected variables are assumed to be measurable, the response surface can be expressed as follows [36] :

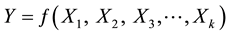
where y is the answer of the system, and x_i the variables of action called factors. The goal is to optimize the response variable (y). The task then is to find a suitable approximation for the true functional relationship between independent variables and the response surface [36] . Usually a second-order model is utilized in response surface methodology:

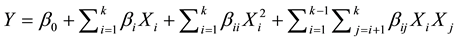
where Y is the predicted response; X₁, X₂, ∙∙∙, X_k are input factors which influence the response y; β₀ is constant; β_i is linear term coefficients; β_ii is quadratic term coefficients; β_ij is cross product term coefficients and K is the number of factors.

2.2. Central Composite Rotatable Design (CCRD)

The experimental design techniques commonly used for process analysis and modeling are the full factorial, partial factorial and central composite rotatable designs. Central composite rotatable design originally developed by Box and Wilson (1951) [37] and improved upon by Box and Hunter (1957) [38] . CCRD gives almost as much information as a three-level factorial, requires many fewer tests than the full factorial design and has been shown to be sufficient to describe the majority of steady-state process responses [39] [40] . Hence in this study, it was decided to use CCRD to design the experiments. The number of tests required for CCRD includes the standard 2k factorial with its origin at the center, 2k points fixed axially at a distance, say β, from the center to generate the quadratic terms, and replicate tests at the center; where k is the number of variables. The axial points are chosen such that they allow rotatability [38] , which ensures that the variance of the model prediction is constant at all points equidistant from the design center. Replicates of the test at the center are very important as they provide an independent estimate of the experimental error. The number of experiments can be detected easily through the following equation: N = K^k + 2K + cp where (k) is the variable number and (cp) is the number of central points [41] [42] .

3. Experimental Work

3.1. Materials

The starting kaolinite clay sample used in the present study was supplied by Central Metallurgical Research and Development Institute, CMRDI, Cairo, Egypt. Its chemical composition is 45% SiO₂, 35% Al₂O₃, 3.5% TiO₂, 1.5% Fe₂O₃, 0.1% MgO, 0.6% CaO, 0.3% Na₂O, 0.05% K₂O and ignition loss nearly 14%. The alkali hydroxide used in the synthesis of zeolite A is NaOH (Alfa Aesar, purity: 97%).

3.2. Synthesis of Zeolite Na-A

Metakolinization is the process in which kaolinite was subjected to calcination at high temperature of about 650˚ C for 5 h where by dehydroxylation occurs forming amorphous more reactive product (metakaolinite). ZeoliteNa-A was synthesized using Egyptian kaolin and sodium hydroxide by treatment of metakaolinite with sodium hydroxide solution with 1:2 weight ratio with a continuous vigorous stirring of the mixture overnight at room temperature. After stirring, the mixture was transferred to 125 ml stainless steel Parr reactors and heated in an oven at 100˚C for 8 h. After hydrothermal treatment, the vessels were cooled down to room temperature. The contents from Teflon vessels were centrifuged to separate solids and solutions. Then, the solid products were washed with distilled water to remove the excess alkalinity and dried at 65˚C.

3.3. Sample Characterization

X-ray powder diffraction patterns were obtained using a Philips APD-3720 diffractometer with Cu Kα radiation, operated at 20 mA and 40 kV in the 2θ range of 5 - 70 at a scanning speed of 5˚/min. Scanning electron microscopy using a field emission scanning electron microscope (JSM-6510, JEOL, Tokyo, Japan). Particle size analyses and surface area of the syntheticzeolite Na-A were determined by BT-2001 (wet) laser particle size analyzer device.

3.4. Adsorption Experiments

Response surface design and central composite rotatable design of quadratic model has been designed according to fours elected variables (Contact time, initial concentration of phosphate, Dosage and pH) to modeling and detect the optimum conditions under which, maximum removal of phosphate from aqueous solution can be occurred. The upper and lower limits for the selected variables in the actual and coded values set in (Table 1). Phosphate stock solutions were prepared by dissolving sodium phosphate dibasic dehydrate in distill water according to the concentrations suggested by the experimental design (Table 2) pH values were adjusted using dilute nitric acid and ammonia solutions.

The experiments were performed according to tests suggested by the statistical design where 25 ml from the prepared solutions shake with the suggested dosage for various contact times then the solutions filtered using 45 µm pore size What man filter paper. The results were evaluated by following phosphate concentration in the filtrate solutions using a spectrophotometric method (DIN EN 1189, 1996) at a wavelength of 700 nm with a Lamp 2 UV/VIS Spectrophotometer. The amount of phosphate ions adsorption onto the zeolite (q (mg/g)) and the removal efficiency were calculated as follows:

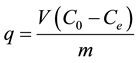
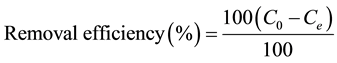
where C₀ and C_e are the ion concentrations in the initial solution and the solution after equilibration of phosphate ions, respectively. V is the volume of solution in (ml) and m is the mass of sorbent (gm).

The data obtained were fitted to a second-order polynomial equation:

.

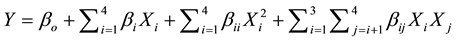where Y is amount of phosphate uptake; β₀, β_i, β_ii, β_ij are constant coefficients X_i are the uncoded independent variables. Subsequent regression analyses, analyses of variance (ANOVA) and response surfaces were performed using the Design Expert Software (Version 6.0.5). Optimal reaction parameters for maximum removal were generated using the software’s numerical optimization function.

4. Results and Discussion

4.1. Characterizations of the Resulted Zeolite

The XRD patterns of the used natural kaolin and metakaolin are shown in Figure 1. Kaolinite and quartz are the

main crystalline phases of untreated kaolin sample (Figure 1). Metakaolin was characterized by the absence of the main diffraction peaks of kaolin at 2θ values of 12.34˚ and 24.64˚ [43] . The main crystalline phase in metakaolin is corresponding to the presence of quartz (Figure 1). X-ray diffraction patterns of synthetic zeolite Na-A samples are shown in (Figure 1). From Figure 1, the synthesized products matched the main peaks of zeolite Na-A at 2θ values of 7.2˚, 10.3˚, 12.6˚, 16.2˚, 21.8˚, 24˚, 26.2˚, 27.2˚, 30˚, 30.9˚, 31.1˚, 32.6˚, 33.4˚ and 34.3˚ that were reported by [44] .

SEM images of zeolite Na-A synthesized by hydrothermal treatment of metakaolinite with sodium hydroxide show the transformation of kaolinite (Figure 2) to well-developed cubic crystals of zeolite Na-A (Figure 2). The SEM results of the present work are similar to those reported in previous studies [19] [23] [43] . The particle size analyses of the studied synthetic zeolite showed that 98% less than 15 μm, 80% less than 9 μm, and 50% less than 5 μm and the surface area gave value 683 m²/g.

4.2. Results of Adsorption Experiments

Table 2 summarizes the experimental runs designed with the CCRD for removal of phosphate from aqueous solution using synthetic zeolite Na-A in terms of the independent variables (contact time, initial concentration, dosage, pH) and the resulted responses (phosphate uptaking (mg) and removal efficiency (%)). The interaction between the selected variables in addition to their effects on different responses are further illustrated.

4.2.1. Fitness of the Statistical Model

The results of analysis of variance (ANOVA) show that, the Model F-values for amount of phosphate uptaking and the removal efficiency are 8.88 and 8.16 respectively which imply that the model is significant; and there is only a 0.04% and 0.06% chances that a “Model F-Value” resulted from noise for the previous stated responses. Pure errors are zero which indicates very good reproducibility of the obtained data. The mathematical equations of the quadratic polynomial model, which represent the relations between the required responses (q(Y₁) and removal efficiency of phosphate (Y₂)) and the selected variables, were obtained from Design Expert Software (Version 6.0.5) for coded units as follows:

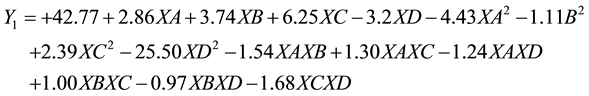
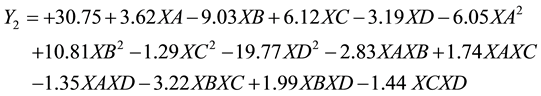
The observed (experimental) values and the predicted values obtained using the model equations are given in Table 3. The predicted values were seen to be sufficiently correlated with the observed values and this reflected

in the high determination coefficient (R²). The closer the R² is to 1, the better the model fits the experimental data, the less the difference between the predicted and the observed values. R² values are above 0.9 for all the required responses as appear in Figure 3(a) for the amount of phosphate adsorbed by synthetic zeolite Na-A and Figure 3(b) for the removal efficiency of phosphate from aqueous solution. This give indication about the significance of the quadratic polynomial model and it is sufficient to represent the actual relations between the required responses and the selected variables.

4.2.2. Effect of Interaction between Operating Parameters

Effect of the selected variables and the interaction between them during removal of phosphate from aqueous solutions using synthetic zeolite Na-A is expressed in 3D and cube response surface diagrams. Response surface plots in terms of two selected factors at any one time maintaining all other factors at fixed levels are suitable in understanding either the main or the interaction effects of these two factors and represented by 3D diagrams. The elliptical shape of the curve indicates good interaction of the two variables and circular shape indicates no interaction between the variables [45] .

The interaction between all the selected variables at fixed pH 4 and their effect on the amount of adsorbed phosphate (mg) and the removal efficiency is represented by cube graphs in Figure 4 and Figure 5 respectively. It is clear that the adsorption of phosphate (mg/g) by zeolite Na-A increase with increasing the contact time, applied dose and the initial phosphate concentrations; and the maximum quantity of phosphate anions removed by the synthetic zeolite Na-A occurs at the upper limits for such selected factors. While the removal efficiency (%) increase with increasing the contact time and the applied dose but decrease with increasing the initial phosphate concentrations.

1) Interaction between contact time and pH

Figure 6(a) shows 3D diagram for the interaction between the contact time and pH values. Plotting the interaction between the contact time and pH values was performed at central fixed amount of synthetic zeolite Na-A (0.08 g) and initial phosphate concentrations (150 mg/L). At any given pH, the amount of the adsorbed phosphate by the synthetic zeolite Na-A increased with increasing the time. The resulted curve show slight slope after 4 h as compared to it from 0.5 h to 4 h i.e. slight variation in the amount of phosphate removed after 4 h. The previous behavior is related to the availability of sorption sites from 0.5 h to 4 h and with time, the number of such active sited reduced which in turn make the adsorption capacity nearly constant [46] . The capacity of the adsorbent to uptake phosphate anions from the solution with time reach the maximum value at acidic pH between 4 and 4.5 and this concordant with [47] .

Effect of pH appears in increasing the adsorption capacity with pH values from pH 2 to pH 4.5 and then reduced from 4.5 to 7. The optimum pH value for maximum capacity is detected to be from 4 to 4.5. Acidic pH is preferred in removal phosphate anions, due to a greater number of surface sites with a PZC = 5.5 at such conditions [48] . The maximum amount phosphate adsorbed at the optimum pH occurs after 4.5 h as contact time.

2) Interaction between initial phosphate concentration and pH

The interaction between initial phosphate concentration and pH values was plotted in Figure 6(b) at fixed dosage (0.08 gm) and contact time (3 h). The amount of adsorbed phosphate anions (mg/g) increased sharply with the initial phosphate concentration at any given pH. Adsorption rate at lower phosphate concentrations is higher as compared to those at higher initial phosphate concentrations specially above 150 mg/L due to the high affinity of the binding sites for phosphate ions and availability of active sorption sites at lower concentrations [45] - [49] . pH values between 4 and 4.5 still the optimum conditions for maximum removal of phosphate anions at any given initial concentration.

Increasing the initial phosphate concentrations has reversible effect on the removal efficiency (%) (Figure 6(c)). Such behavior may be attributed to the adsorption capacity of the synthetic zeolite Na-A. Increasing the initial phosphate concentrations provide more phosphate ions, while the fixed amount from the used adsorbent has a fixed number of sorption sites. Therefore the maximum uptake (mg/g) occur at the upper limit for the initial concentrations, while the maximum removal efficiency (%).

3) Interaction between solid dosage and pH

Figure 6(d) represents the response surface plotting of the interaction between the amount of zeolite Na-A (gm) and pH values at fixed contact time (3 h) and initial phosphate concentrations (150 mg/L). Quantities of adsorbed phosphate anions by zeolite increased with increasing adsorbent dose at any given pH. This related to the increase in the total surface area of the adsorbent particles and the available sorption active sites [1] -[50] . Middle pH from 4 to 4.5 still the optimum pH. The maximum capacity for phosphate uptaking and the best conditions for maximum removal efficiency (%) (mg/g) occurs within this range and at the upper limit for the amount of the zeolite.

4) Interaction between adsorbent dosage and the contact time

The relation between amounts of zeolite Na-A and contact times during the adsorption process represented in Figure 7(a). The interaction effect was performed at fixed pH (4.5) and initial concentration (150 mg/L). The resulted curve revealed that the adsorption capacity increase with increasing both the contact time and the amount of zeolite. The interaction effect appears in increasing the effect of the contact time with increasing the dose to the maximum value at 0.1 gm. The maximum effect for the amount of zeolite occur after 4.5 h then the efficiency reduced i.e. 0.1 gm dose and 4.5 h contact time are the optimum conditions.

5) Interaction between contact time and initial concentrations

The interaction between the contact time and the initial phosphate concentration was investigated at pH 4.5 and dosage 0.08 gm and represented in Figure 7(b). From Figure 7(b), the amount of the adsorbed phosphate increases with the contact time at any given concentration, but the effect of time increase to the maximum effect with increasing the initial phosphate concentration to the upper limit (250 mg/L). However the adsorption capacity increases with increasing the initial phosphate concentration at any given time, but the maximum effect occur after about 4.5 h and then the efficiency decreased.

Figure 7(c) represents the effect of time and concentration on the removal efficiency (%). It is clear that the removal efficiency increase with time at any concentration, but it increase at lower concentrations and the maximum value occur at 50 mg/L. 4.5 h contact time represent the best time for the removal efficiency. In the other hand the efficiency decrease with increasing the initial concentration to the minimum value at 250 mg/L. the previous make 4.5 h as contact time and 50 mg/L as initial phosphate concentration the best conditions for maximum removal efficiency based on the upper and the lower limits of the selected parameters.

6) Interaction between dosage and the initial concentration

The relation between zeolite dosage and initial phosphate concentrations; and their effect on the required responses is represented in Figure 7(d) and Figure 7(e). This was performed at fixed pH 4.5 and contact tome 3 h. It is clear that, at any given initial phosphate concentration the amount of adsorbed phosphate (mg/g) increase with the amount of zeolite and the effect of the dose increase with increase the concentration to 250 mg/L (Figure 7(d)). Also the removal efficiency increase with increasing the dose at any given concentration but appear to be more promising at lower concentrations (Figure 7(e)). Also the amount of adsorbed phosphate increase with increasing the initial concentrations at any given dose while the removal efficiency decrease with increasing the initial concentration and the best values obtained when the applied dose is the upper limit (0.1 gm).

5. Optimum Conditions

Observed experimental results in Table 2 show that at 3 h as contact time, 150 mg/L initial phosphate concentration in the aqueous solution, 0.1 gm solid dose and pH₄ are the best conditions with respect amount of phosphate adsorbed by the synthetic zeolite Na-A (53 mg/g), but the maximum removal efficiency (60%) occur after 3 h as contact time, 50 mg/L initial concentration for phosphate in the aqueous solutions, 0.08 gm dose and pH₄.

The predicted optimum conditions for maximum phosphate anions removal using synthetic zeolite Na-A have been predicted using Design Expert’s optimization function in terms of the upper and lower limits for the selected variables (contact time, initial concentrations, dose and pH). The optimum conditions are listed in Table 4 and Table 5 with their predicted values. 4.5 h contact time, 50 ppm initial concentration, 0.1 zeolite dose and pH 4.04 are the optimum conditions for maximum removal of phosphate (%) by synthetic zeolite Na-A with predicted removal efficiency 61.77%. While contact time of 4.52 h, 250 mg/L initial phosphate concentration, 0.1 zeolite Na-A dose and 4.14 pH are the predicted optimum conditions for the maximum adsorption of phosphate anions (55.82 mg/g).

6. Conclusions

Highly crystalline synthetic Na-A was synthesized from Egyptian kaolinite by hydrothermal treatment of metakaolinite at 100˚C for 8 h. In this study, response surface methodology in conjunction with central composite rotatable design was employed for modeling and optimizing four operations parameters of phosphate removal using synthetic zeolite Na-A. Four variables of the model investigated in this study were: contact time, initial phosphate concentration, amount of zeolite and pH values. The mathematical model equations were derived for both amount of phosphate adsorbed (mg/g) and the removal efficiency (%) from Design Expert Software (Version 6.0.5). Predicted values obtained using the model equations were in very good agreement with the observed values (R² value of 0.918 for the amount of the adsorbed phosphate, R² value of 0.905 for the removal efficiency (%)).

In order to gain a better understanding of the effects of these operational variables and their interactions on the amount of adsorbed phosphate (mg/g) and the removal efficiency (%), the predicted models values were

presented as cube and 3D response surface graphs. Taking advantage of the quadratic programming, contact time of 4.5 h, initial concentration of 50 ppm, zeolite dose of 0.1 gm and pH of 4.04 have been determined as optimum levels to achieve the maximum removal of phosphate of 61.77%, whereas it is 60% in the tests conducted, i.e. 1.77 improvements in the removal efficiency could be obtained by the statistical design. In the same way, contact time of 4.52 h, initial concentration of 250 ppm, zeolite dose of 0.1 gm and pH of 4.19 have been determined as optimum levels to achieve the maximum amount of phosphate anions adsorbed by synthetic zeolite Na-A as it reaches (55.82 mg/g); however, the best result from the experimental tests is (53 mg/g).

Cite this paper

E. A.Mohamed,A. Q.Selim,M. K.Seliem,Mostafa R.Abukhadra, (2015) Modeling and Optimizations of Phosphate Removal from Aqueous Solutions Using Synthetic Zeolite Na-A. Journal of Materials Science and Chemical Engineering,03,15-29. doi: 10.4236/msce.2015.39003

References