Journal of Materials Science and Chemical Engineering
Vol.02 No.11(2014), Article ID:51109,5 pages
10.4236/msce.2014.211003
On the Advantages of the Theories of Plasticity with Singular Loading Surface
Andrew Rusinko, Daniel Fenyvesi
Donát Bánki Faculty of Mechanical and Safety Engineering, Óbuda University, Budapest, Hungary
Email: ruszinko.endre@bgk.uni-obuda.hu, fenyvesi.daniel@bgk.uni-obuda.hu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 September 2014; revised 4 October 2014; accepted 25 October 2014
ABSTRACT
This paper analyzes the peculiarities of plastic flow of metals for the case of non-proportional loading when the loading path consists of two portions—uniaxial tension and subsequent infinitesimal pure shear (torsion). The issue is discussed from the point of view of the hardening rules governing the kinetics of loading surface. Three cases are considered, flow plasticity theory with isotropic and kinematic hardening rule, as well as the synthetic theory of plastic deformation. As a result, the synthetic theory leads to the results that correlate with experiments, whereas the former two theories associated with smooth loading surfaces give a principal discrepancy with experimental data.
Keywords:
Plastic Deformation, Loading Path, Synthetic Theory

1. Introduction
The overwhelming majority of the theories of plastic deformation of metals address the notion of yield and loading surface to give a geometrical interpretation of the onset and development of plastic strains. This paper will analyze (i) plastic flow theories with smooth loading surfaces and (ii) results obtained in terms of the synthetic theory of irrecoverable deformation for the case of a non-proportional loading. Consider a loading path
consisting of two parts in stress space (Figure 1): AB—proportional loading  beyond the yield limit of material in uniaxial tension
beyond the yield limit of material in uniaxial tension 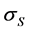 and BC—infinitesimal additional loading
and BC—infinitesimal additional loading 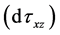 at right angle to AB potion. According to Sveshnikova [1] , such loading regimes result in the increment of plastic deformation
at right angle to AB potion. According to Sveshnikova [1] , such loading regimes result in the increment of plastic deformation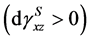 .
.
Sveshnikova’s experiments were carried out on thin-walled cylinders loaded in uniaxial tension and the additional loading was obtained by the twisting of the specimens.
Figure 1. Loading path ABC in Sveshnikova’s experiment.
The goal of the paper is to show that the synthetic theory is capable of describing the occurrence of the increment of plastic deformation due to the additional loading, whereas the theories with smooth loading surfaces lead to the absence of plastic flow, which is contradictive to the experimental results. Although the problem dates back to the 20th century, it remains unsolved till now. The issue of the occurrence of plastic deformation due to an infinitesimal additional loading, nevertheless, is of high importance. Indeed, as is often the case, structural members working under some stress state are subjected to a small additional loading resulted from sudden overloading or lack of fit. Such a situation is typical, e.g. beams deformed by bending and undergoing small torsions.
The occurrence of the increments of plastic strains due to the additional loading is studied in a geometrical way, by means of the analysis of loading surfaces. In terms of the synthetic theory [2] [3] , an additional orthogonal loading leads to the occurrence of additional plastic deformation (which can be calculated by the formulae presented in [2] [3] ), which is not the case in the framework of the theories providing smooth loading surfaces.
2. Smooth Loading Surface under Two-Sectional Loading Path
Consider the behavior of material modeled by the flow theories based on the isotropic and kinematic hardening rule [3] - [6] for the following loading path (as shown in Figure 1): uniaxial tension and subsequent orthogonal additional loading (infinitesimal torsion).
In isotropic hardening, the yield surface increase in size due to the stress vector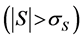
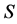 , but remain the
, but remain the
same shape, as a result of plastic straining (Figure 2(a)). This condition in the three dimensional subspace,  , of the Ilyushin five-dimensional space
, of the Ilyushin five-dimensional space  [3] [5] , can be expressed as
[3] [5] , can be expressed as
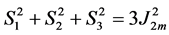 (1)
(1)
where 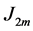 is the maximum value of the second invariant of stress deviator tensor
is the maximum value of the second invariant of stress deviator tensor  [4] for the whole history of loading.
[4] for the whole history of loading.
According to kinematic hardening rule, the yield surface remains the same shape and size but merely translates in stress space (Figure 2(b)), which can be expressed by the following equation:
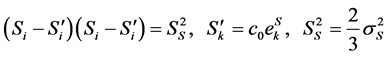 (2)
(2)
where 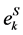 is the plastic strain vector components [3] [5] ,
is the plastic strain vector components [3] [5] ,  constant.
constant.
Equations (1) and (2) give the von-Mises yield criterion when 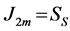 and
and 

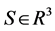



where 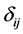



Now, consider the infinitesimal additional loading



Figure 2. Direction of additional loading vector dS (0, 0, dτxz) with respect to the loading surface in terms of isotropic (a) and kinematic (b) hardening rule in S1 - S3 coordinate planes.
S1-axis (Figure 2(a) and Figure 2(b)). In terms of flow plasticity theories, this means that the additional loading 

Therefore, although the theories discussed above are widely used for the modelling of the plastic strains of metals, they are incapable of catching the phenomenon registered in [1] .
3. Fundamentals of the Synthetic Theory
The synthetic theory is based on the Batdorf-Budiansky slip concept [7] and the Sanders flow theory [8] and deals with small irrecoverable (plastic/creep) deformations of hardening materials.
Similarly to the Batdorf-Budiansky concept, the deformation of material is calculated on its two structural levels: macro- and micro-level. A point of a body is considered as an elementary volume of the body,












The modeling of irrecoverable deformation at a point of a body 





where 
According to Sanders [8] , through each point on the sphere we draw a tangent plane. So, the yield surface can be thought of the inner envelope of the equidistant planes.
The position of plane in 


















To establish a hardening rule, which governs the kinetics of loading surface during plastic flow, we extend the provision that a surface can be constructed as an inner envelope of planes to the case of loading as well. In the
Figure 3. Two levels of material structure: an elementary volume of loaded body (V) consists of grains (slip systems) V0 producing deformation on microlevel.
Figure 4. Distance to plane HN and the orientation of vector m.
course of loading, the vector 

Each tangent plane corresponds to an appropriate slip system

As it follows from Equation (4) and the hardening rule, material is considered initially isotropic, but after the development of irrecoverable strain its properties (e.g. hardening) become definitely anisotropic.
The condition that a plane in 

where the product 


An average measure of irrecoverable strain within one slip system




Figure 5. Displacement of plane on the endpoint of stress vector (a) and loading-surface (b) in terms of the synthetic theory.

Macro-deformation is defined by a strain vector, 



The upper and lower integration limits in (8) are obtained from the condition 


Summarizing, the magnitude of plastic deformation rate depends on the set of planes located on the endpoint of
4. Synthetic Theory for Two-Sectional Loading Path
Let us study if an additional plastic strain increment occurs due to the additional loading 



Figure 6. Orientation of additional stress-vector dS with respect to the loading surface in terms of the synthetic theory.
This fact means that the action of the 



Therefore, in the framework of the synthetic theory, the phenomena of the occurrence of plastic deformation on the orthogonal portion of additional loading can be modelled, this fact is of great importance since is not the case for the flow theories with smooth loading surface.
5. Conclusion
The formation of corner point (conical singularity) on the loading surface during plastic straining is of crucial importance for the correct formulation of the theories of plasticity. As it has been shown in this paper, the flow plasticity theories based on hardening rules with smooth loading surfaces lead to non-conformity with the experimental result obtained for the case of non-proportional loadings (they give no increment in plastic strain), e.g. when the loading path is a broken line with orthogonal portions. At the same time, the synthetic theory of plastic deformation shows the occurrence of plastic straining in the additional loading even without calculations; it is immediately seen from the shape of loading surface and the direction of additional loading.
Acknowledgements
The authors expresses thanks to Prof. K. Rusinko (Budapest University of Technology and Economics, Hungary) for many useful conversations on the topics presented in this article.
References
- Sveshnikova, V.A. (1956) Plastic Deformation of Strain-Hardening Metals. Izvestija Akademii Nauk SSSR, Otdelenie Tekhnicheskikh Nauk, No. 1, 155-161. (In Russian)
- Rusinko, A. and Rusinko, K. (2009) Synthetic Theory of Irreversible Deformation in the Context of Fundamental Bases of Plasticity. Mechanics of Materials, 41, 106-120. http://dx.doi.org/10.1016/j.mechmat.2008.09.004
- Rusinko, A. and Rusinko, K. (2011) Plasticity and Creep of Metals. Springer, Berlin and Heidelberg. http://dx.doi.org/10.1007/978-3-642-21213-0
- Chen, W.F. and Han, D.J. (1988) Plasticity for Structural Engineers. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-3864-5
- Ilyushin, A.A. (1963) Plasticity. Izdatelstvo Akademii Nauk SSSR, Moscow. (In Russian)
- Hill, R. (1998) The Mathematical Theory of Plasticity. Clarendon Press, oxford.
- Batdorf, S. and Budiansky, B. (1949) Mathematical Theory of Plasticity Based on the Concept of Slip. NACA Technical Note, 871.
- Sanders Jr., J.L. (1954) Plastic Stress-Strain Relations Based on Linear Loading Functions. Proceedings of the Second USA National Congress of Applied Mechanics, Ann Arbor, 14-18 June 1954, 455-460.
- Rusinko, A. (2014) Feigen’s Phenomenon in Terms of the Synthetic Theory. International Journal of Engineering Research and Applications, 4, 172-180.








