ABSTRACT

Software complexity crisis brings huge obstacle to further progress in IT industry. To alleviate this problem, researchers are asked to build systems which can benefit from automation. With autonomic behavior, the real-time reactive systems can be more self-managed and adaptive to their environment. However, most of current formal approaches fail to specify such kind of system. In this paper, we proposed an approach to formally specify reactive autonomic systems. First, we used category theory to formalize reactive autonomic systems; then we focused on the categorization of self-configurations and work flows of reactive autonomic systems, and finally we used XML to specify the categorical models. In doing so, it can help to build the foundation of reactive autonomic systems with autonomic features and verify emergent behaviors.

Keywords:

Reactive Autonomic System, Category Theory, XML, Self-Configuration

1. Introduction

Real-time reactive systems can be very complex, and difficult to test and error-finding. Race conditions in real-time reactive systems are hard to be found by only inputting sample data and checking the results, as certain errors are time-based and only occur when processes send or receive data at particular time, in particular in sequence or after learning. In order to find those errors, all possible state combinations of the processes have to be executed, which are exponential in the number of states [1] . Formal method could provide systems with known safety properties since a formal specification can be used to check for particular types of errors and as inputs for model checking. Category theory has been proposed as a framework to offer specification structure. It has a rich body of theory to reason objects and their relations. Moreover, category theory adopts a correct by construction approach by which components can be specified, proved and composed in the way of preserving their properties. Unfortunately, most of current formal approaches fail to specify Reactive Autonomic System (RAS) and do not address well on verifying emergent behaviors, which is an important characteristic for the RAS.

To handle above mentioned problem, as a continuation of research [2] [3] [4] , we first discuss how to model RAS and its configurations in category theory; then, we show how to transform the self-configuration properties to the categorical representations, and we use XML to specify the representations. The rest of this paper is organized as follows: Section 2 gives an overview of the related work. Section 3 introduces background knowledge required to understand the remaining content of the paper. Section 4 introduces categories that represent RAS model and its configurations respectively. Section 5 shows how to transform the categorical self-configuration and the properties into categories, and uses XML to specify the categories. Finally, Section 6 concludes the work.

2. Related Work

In this section, research work related to this paper is introduced.

2.1. Real-Time Reactive Systems

Seshia proposes an architecture for automatically recovering a class of reactive systems from run-time failures [5] . The system comprises executions which can be divided into several rounds and each round performs a new unit of work. The framework leverages parallelism to proactively explore the space of repairs before a failure is occurred. Paper [6] presents a self-adapting loop according to system-specific adaptation knowledge that includes the types and properties of autonomic components, behavior constraints as well as strategies for adaptation. This system is an integral part of a real-time system which controls the behavior of computing environment and evaluates its global behavior.

2.2. Formal Methods

For modeling concurrency, category theory is used to model, analyze, and compare Transition System, Trace Language, Event Structure, Petri nets, and other classical models of concurrency [7] [8] [9] . Mackworth and Zhang describe a Constraint-Based Agent (CBA) design approach which includes two formal models: Constraint Nets and Timed ∀-automata [10] . A constraint net can model agents and their environment symmetrically as dynamical systems; timed ∀-automata can specify desired real-time dynamic behaviors of those situated agents. Paper [11] introduces a formal language model which formalizes agent- environment interaction in a multi-agent framework called Conversational Grammar Systems (CGS). This system provides a model with a high degree of flexibility. Based on eco-grammar systems, the formal model used in this paper can be defined as an evolutionary multi-agent system. Category theory is applied to study relationships between geometrical models for concurrency and classical models [12] .

3. Background

In this section, background and work related to our research are introduced.

3.1. Reactive Autonomic Systems (RAS)

The Reactive Autonomic Systems (RAS) architecture model (Figure 1) is a four-layer architecture that consists of Reactive Autonomic Objects (RAO), Reactive Autonomic Components (RAC), Reactive Autonomic Component Groups (RACG) as well as the RAS. The autonomic features are implemented by RAO Leaders (RAOL), RAC Supervisors (RACS) and RACG Managers (RACGM) at the RAC, RACG as well as RAS layer respectively [2] . In this layered architecture model, each tier communicates only with the tier immediately above or below it. Thus, the independence of those tiers makes their modularity, encapsulation, hierarchical decomposition and reuse possible.

1) RAO is modeled as a labeled transition system augmented with ports, resources, attributes and the logical assertion on those attributes as well as time constraints [13] . More specifically, it is modeled as a 9-tuple (P, ε, Θ, X, L, Φ, Λ, γ, R) where P, ε, Θ, X, L, Φ, Λ, γ are specified as in [14] :

・ P is a finite set of ports associated with each port-type and the null-type P₀ whose only port is the null port P₀.

・ ε is a finite set of events and includes the silent-event tick.

・ Θ is a finite set of states where Θ₀: Θ, is the initial state; there is no final state.

・ X is a finite set of typed attributes: abstract data types and port reference types.

・ L is a finite set of LSL traits for the abstract data type used in X.

・ Φ is a function-vector (Φ_s, Φ_at) which Φ_s associates with each state Θ a set of sub states and Φ_at associates with each state Θ a set of attributes.

・ Λ is a finite set of transition specifications.

・ γ is a finite set of time-constraints.

・ R models the set of resources available locally for the object to support its functionality.

2) RAC is a set of synch.

Ronously communicating RAO, where one of the RAO is assigned as a leader (RAOL) of the rest (workers). The workers are responsible for reactive tasks, while the RAOL works on autonomic tasks such as coordinating the self-monitoring at component level. Thus, the RAOL has a different set of states from the workers, which states are autonomic behavior related instead of reactive behavior related. The reactive and autonomic natures of formal specifications for the RAOL enable them to implement autonomic functionalities in a real-time reactive system. In order to coordinate the work as well as communication between the RAO, a RAC specification consists of Members, Configure, Leader, Supervisor, Neighbors and Repository. The RAC is the minimum centralized Reactive Autonomic Element (RAE) that has the ability of self-management in RAS.

Similarly to the RAO, the reactive behavior of a RAC consists of n collaborating. RAO is specified as a 9-tuple (P^syn, ε^syn, Θ^syn, X^syn, L^syn, Φ^syn, Λ^syn, γ^syn, R^syn) [13] :

・ P^syn is a set of port-types allowing for a synchronous communication between the RAO.

・ ε^syn is a union of all ε_i where i: [1 ... n].

・ Θ^syn is a finite set of reachable and valid Synchronous Production Machine (SPM) state.

・ X^syn is a union of the finite sets $X_1^{\text{syn}}$ , …, $X_{\text{n}}^{\text{syn}}$ .

・ L^syn is a union of the finite sets of Larch Specification Language (LSL) traits for Abstract Data Type (ADT) used in the RAO.

・ Φ^syn is a function-vector ( ${\Phi }_{\text{s}}^{\text{syn}}$ , ${\Phi }_{\text{at}}^{\text{syn}}$ , ${\Phi }_{\gamma }^{\text{syn}}$ ) that ${\Phi }_{\text{s}}^{\text{syn}}$ associates with each SPM state Θ^syn a set of sub states and ${\Phi }_{\text{at}}^{\text{syn}}$ associates with each SPM state Θ^syn the uniton of the set of attributes a set of attributes Φ_at1( ${\Theta }_{\text{1}}^{\text{syn}}$ ), …, Φ_atn( ${\Theta }_{\text{n}}^{\text{syn}}$ ): ${\Phi }_{\gamma }^{\text{syn}}$ associates each SPM state Θ^syn with a subset of R^syn.

・ Λ^syn is a finite set of transition specifications.

・ γ^syn is a finite set of time-constraints.

・ R^syn is a set of resources available in the RAO; it is defined as a union of all R_i: i: [1 ... n].

3) RACG is a set of centralized or distributed RAC that cooperate in fulfillment of group tasks by synchronous communications. It is the minimum RAE which can independently accomplish complete real-time reactive tasks in RASF. The autonomic behavior at group level is coordinated by a supervisor (RACS).

4) RAS is made up of centralized or distributed RACG with asynchronous communication. It provides an integrated interface for users to delegate computing tasks, monitor systems and manage repositories. A manager (RACGM) is responsible for coordinating autonomic behavior at system level.

3.2. Self-Configuration in Reactive Autonomic Systems

Self-configuration is an essence of RAS. Components in RAS are able to configure themselves automatically according to high level policies (business level objectives), which specify what is required instead of how they are implemented. The self-configuration work flows of RAC, RACG and RAS are represented in sequence diagrams are illustrated in Figures 2-4 respectively.

3.3. Category Theory

Category theory has a rich body of theory to reason objects as well as their relations, and it is abstract enough for a wide range of different specification languages [15] . Categorytheory for the software specification has adopted a correct by construction approach by which components are specified, proved and composed in the way of preserving their properties [15] . Moreover, category theory can provide techniques to manipulate and reason diagrams for building hierarchies of system complexity, allowing systems to be used as components of more complex systems and inferring properties of the systems from their configurations [12] .

As there is no such kind of formalization for self-configurations of RAS, we propose to use category theory to formalize the self-configurations. To understand this paper, we introduce the definition of category.

Definition 1: A category consists of objects and morphisms. A morphism f: A → B has object A as its domain and object B as its codomain, respectively. If there are morphisms f: A → B and g: B → C, then there is also a morphism g f: A

→ C called their composition. Composition is associative: (h ◦ g) ◦ f = h ◦ (g ◦ f). Every object X has an identity morphism Id_X. For every morphism f: A → B, Id_B ◦f = f = f ◦ Id_A.

4. Categorical Representations of RAS Model

In order to categorize the self-configuration of RAS, we need to formalize RAS model by using category theory first. In this section, we build categorical representations of RAS model including RAC, RACG, and RAS.

Proposition 1: RAC can be specified as a category RAC with a set of objects |RAC| and morphisms so that for each RAO_i, RAO_j Î |RAC|, there is a set of morphisms f: RAC (RAO_i, RAO_j) mapping the RAO_i to RAO_j which indicate the communication between them as f: i RAO_i → RAO_j。

Proof: All what we need is to prove: 1) the existence of composition and identity morphism, and 2) prove associativity. Let RAO₁, RAO₂ and RAO₃ be three RAO such that RAO₁ can interact with RAO₂, which can interact with RAO₃. Then RAO₁ can communicate with RAO₃ (indirectly through RAO₂), which means the existence of a composition of morphisms between RAO₁ and RAO₃. The identity morphism does exist as a natural representation of internal communications. Let f, g and h be the morphisms such that f: RAO₁ → RAO₂, g: RAO₂ → RAO₃ and h: RAO₃ → RAO₄. It is clear that h ◦ (g ◦ f) = (h ◦ g) ◦ f.

Proposition 2: The RACG may also be specified as a category RACG with a set of objects |RACG| and morphisms such that for each RAC_m, RAC_n Î |RACG|, there is a set of morphisms f: RACG (RAC_m, RAC_n) mapping the RAC_m to the RAC_n that indicate the communication between them as f: RAC_m → RAC_n.

Proof: All what we need is to prove: 1) the existence of composition and identity morphism, and 2) prove associativity. Let RAC₁, RAC₂ and RAC₃ be three RAC such thatRAC₁ can interact with RAC₂, which can interact with RAC₃. Then RAC₁ can communicate with RAC₃ (indirectly through RAC₂), which means the existence of a composition of morphisms between RAC₁ and RAC₃. The identity morphism does exist as a natural representation of internal communications. Let f, g and h be the morphisms such that f: RAC₁ → RAC₂, g: RAC₂ → RAC₃ and h: RAC₃ → RAC₄. It is clear that h ◦ (g ◦ f) = (h ◦ g) ◦ f.

Proposition 3: The RAS may also be specified as a category RAS with a set of objects |RAS| and morphisms such that for each RACG_x, RACG_y Î |RAS|, there is a set of morphisms f: RAS (RACG_x, RACG_y) mapping the RACG_x to the RACG_y that indicate their communications as f: RACG_x → RACG_y.

Proof: All what we need is to prove: 1) the existence of composition and identity morphism, and 2) prove associativity. Let RACG₁, RACG₂ and RACG₃ be three RACG such that RACG₁ can communicate with RACG₂, which can interact with RACG₃. Then RACG₁ can interact with RACG₃ (indirectly through RACG₂), which means the existence of a composition of morphisms between RACG₁ and RACG₃. The identity morphism does exist as a natural representation of internal communications. Let f, g and h be the morphisms such that f: RACG₁ → RACG₂, g: RACG₂ → RACG₃ and h: RACG₃ → RACG₄. It is clear that h ◦ (g ◦ f) = (h ◦ g) ◦ f.

Figure 5 illustrates the categorical representations and the corresponding proofs in Proposition 1 - 3.

5. Categorical Representations of Self-Configurations of RAS Model

Based on the categorical representations of RAS model in Section 3, in this section,

we build categorical representations of self-configurations of RAS model, and use xml to specify the categories.

Proposition 4: The configuration of a RAC is a category denoted as CONFIG (RAC), where objects are RAO and morphisms are connections between those RAO as CONFIG (RAO_i, RAO_j) or CONFIG (RAO_j, RAO_i).

Proof: The proof of Proposition 4 is similar to the proof of Proposition 1, where the morphism connection in Proposition 4 is similar to the morphism communication in Proposition 1.

The XML specification of the category CONFIG (RAC) can be described as follows:

Proposition 5: The configuration of a RACG is the category denoted as CONFIG (RACG), where objects are RAC and morphisms are connections between those RAC as CONFIG (RAC_i, RAC_j) or CONFIG (RAC_j, RAC_i).

Proof: The proof of Proposition 5 is similar to the proof of Proposition 2, where the morphism connection in Proposition 5 is similar to the morphism communication in Proposition 2.

The XML specification of the category CONFIG (RACG) can be described as follows:

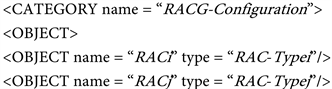
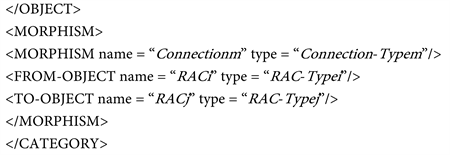
Proposition 6: The configuration of a RAS is a category denoted as CONFIG (RAS), where objects are RACG and morphisms are the connections between those RACG as CONFIG (RACG_i, RACG_j) or CONFIG (RACG_j, RACG_i).

Proof: The proof of Proposition 6 is similar to the proof of Proposition 3, where the morphism connection in Proposition 6 is similar to the morphism communication in Proposition 3.

The XML specification of the category CONFIG (RAS) can be described as follows:

As introduced in Section 1, the self-configurations of RAC, RACG, and RAS follows the work flow illustrated in Figures 2-4. For each work flow, we can build a category for it, and use XML to specify the corresponding category.

Proposition 7: The self-configuration work flow of RAC is a category denoted as CONWORKFLOW (RAC), where its objects are messages Validate RAOL, ValicateRAO, LunchInvestigation, ValidateRAOCommunication, Conform, NotConform, and the morphisms denote the relationship before between the occurrences of objects before₁: ValidateRAOL → Conform, before₂: ValidateRAOL → NotConform, before₃: ValidateRAO → Conform, before₄: ValicateRAO → NotConform, before₃: ValidateRAOCommunication → Conform, before₆: ValicateRAOCommunication → NotConform, before₇: NotConform → LunchInvestigation.

Proof: All what we need is to prove: 1) the existence of composition and identity morphism, and 2) prove associativity. Let Obj₁, Obj₂ and Obj₃ be three messages such that Obj₁ occurs before Obj₂, which occurs before Obj₃. Then Obj₁ occurs before Obj₃ (indirectly through Obj₂), which means the existence of a composition of morphisms between Obj₁ and Obj₃. The identity morphism does exist as a natural representation of interactions with occurrence. Let f, g and h be the morphisms such that f: Obj₁ → Obj₂, g: Obj₂ → Obj₂ and h: Obj₃ → Obj₄. It is clear that h ◦ (g ◦ f) = (h ◦ g) ◦ f.

The XML specification of the category CONWORKFLOW (RAC) can be described as follows:

Proposition 8: The self-configuration work flow of RACG is a category denoted as CONWORKFLOW (RACG), where its objects are messages ValidateRAC, ValicateRAOL, LunchInvestigation, ValidateRAOLCommunication, Conform, NotConform, and the morphisms denote the relationship before between the occurrences of objects before₁: ValidateRAC → Conform, before₂: ValidateRAC → NotConform, before₃: ValicateRAOL → Conform, before₄: ValicateRAOL → NotConform, before₃: ValidateRAOLCommunication → Conform, before₆: ValidateRAOLCommunication → NotConform, before₇: NotConform → LunchInvestigation.

Proof: The proof of Proposition 8 is omitted, as it is similar to the proof of Proposition 7.

The XML specification of the category CONWORKFLOW (RACG) can be described as follows:

Proposition 9: The self-configuration work flow of RAS is a category denoted as CONWORKFLOW(RAS), where its objects are messages ValidateRACG, ValicateRAC, LunchInvestigation, ValidateRACCommunication, Conform, NotConform, and the morphisms denote the relationship before between the occurrences of objects before₁: ValidateRACG → Conform, before₂: ValidateRACG → NotConform, before₃: ValidateRAC → Conform, before₄: ValicateRAC → NotConform, before₃: ValidateRACCommunication → Conform, before₆: ValidateRACCommunication → NotConform, before₇: NotConform → LunchInvestigation.

Proof: The proof of Proposition 9 is omitted, as it is similar to the proof of Proposition 7.

The XML specification of the category CONWORKFLOW (RACG) can be described as follows:

6. Conclusion

Due to the difficulties of test and error-finding in real-time reactive systems, in this paper, we proposed an categorical approach to formally specify reactive autonomic systems and the self-configuration work flows, which can help to check for particular types of errors and as inputs for model checking. Moreover, we used XML to specify the constructed categorical models, which can help to build the foundation of reactive autonomic systems. By adopting the categorical approach, the construction of reactive autonomic systems and the self-configuration work flows can be specified, proved and composed formally with preserving their properties. In future, we will work toward building a categorical framework to verify the correctness of the construction of reactive autonomic systems, based on the proposed categorical specification.

Acknowledgements

We thank the Editor and the referee for their comments. Research of M. Zhu and J. Li is funded by the Shandong University of Technology grants 4041-416069 and 4041-417010. The support is greatly appreciated.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Cite this paper

Zhu, M., Kuang, H. and Li, J. (2018) Representation of Categorical Specification of Self-Configurations in Reactive Autonomic Systems Framework. Journal of Computer and Communications, 6, 34-48. https://doi.org/10.4236/jcc.2018.612003

References