Journal of Computer and Communications
Vol.04 No.06(2016), Article ID:66918,12 pages
10.4236/jcc.2016.46003
Digital Refocusing: All-in-Focus Image Rendering Based on Holoscopic 3D Camera
Obaidullah Abdul Fatah, Peter Lanigan, Amar Aggoun, Mohammad Rafiq Swash
College of Engineering, Design and Physical Sciences, Brunel University, London, UK

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 March 2016; accepted 27 May 2016; published 30 May 2016
ABSTRACT
This paper presents an innovative method for digital refocusing of different point in space after capturing and also extracts all-in-focus image. The proposed method extracts all-in-focus image using Michelson contrast formula hence, it helps in calculating the coordinates of the 3D object location. With light field integral camera setup the scene to capture the objects precisely positioned in a measurable distance from the camera therefore, it helps in refocusing process to return the original location where the object is focused; else it will be blurred with less contrast. The highest contrast values at different points in space can return the focused points where the objects are initially positioned as a result; all-in-focus image can also be obtained. Detailed experiments are conducted to demonstrate the credibility of proposed method with results.
Keywords:
Holoscopic 3D Image, Integral Image, Viewpoint, 3D Image, Digital Focusing, Light Field Image

1. Introduction
Holoscopic 3D imaging also known as 3D imaging is on the verge of constant development in the scientific as well as the entertainment community in recent years. Currently 3D capturing methods are complicated and extensively expensive requiring complex multiple camera configurations for clever image registration and focusing to obtain multiple perspective views of the scene [1] . In these systems setup, depth information of 3D object is extracted by estimating disparities between two or multiple camera’s frames [2] [3] . However, researchers seek to come up with alternative solution to compensate the complexity of complicated and expensive multiple camera configurations to capture 3D content. Therefore, two well recognised methods holography [4] and inte- gral (Holoscopic) imaging [5] are seen as the future alternatives for capture and display of 3D content.
Holographic technology [6] offers full parallax but due to the interfering of coherent light fields required to record holograms its practicality is heavily reduced. Whereas integral imaging/plenotic/integral imaging systems, which are based on integral photography, offer the simplest form of recording the true 3D content with continuous parallax. The first person to pioneer the integral photography is G. Lippmann [7] . In recent years, increase in processing power and storage capabilities makes this proposed method as an ideal system amongst other existing 3D technologies. Furthermore its advantages amongst existing 3D technologies, it offers full parallax in real-time recording without complicated and expensive camera calibration, free from eye strain [8] and uses natural light. This increases its practicality and promises beyond the capabilities of traditional cameras, as it offers refocusing and depth of field that can be well adjusted after capturing.
2. Related Works
In the past few years, integral technology is achieving greater acceptance due to the mass progress made in microlens manufacturing, to improve numerous hardware implications. Such as increasing the viewing angle and provided pseudoscopic images [9] - [11] . Other than hardware implication, there are image processing issues. The most important is the 3D reconstruction with aid of depth information. It is very vital to obtain depth information to enable both content-based image coding and content-based interactive manipulation in correcting spatial resolution analysis. Since depth information is recorded in 2D format, as a result, it promises to provide other application where depth information is necessary, such as biometrics, medical imaging, robotic visions and many other [12] .
Depth extraction of 3D objects in the real world has been known as one of the important challenges in the field of machine vision, target recognition, tracking and video surveillance [13] . However, the depth extraction from 3D integral imaging was first recorded by Manolache et al. [14] , using point-spread function of the optics. The depth calculation is tackled as an inverse problem due to image inversion. Therefore, the discrete correspondents are ill conditioned and loss of information associated with the model in the direct process. Recently, the plenoptic camera system has been extensively studied to open up new possibilities by enabling the operator to adjusts the depth of field after an image had been captured [15] [16] and [17] [18] . Currently plenoptic cameras are mainly used for refocusing in photography and the images rendered in Ng are in low resolution. Since Ng uses the angular ray information that is referred to the viewpoint image in refocusing, the resolution is determent by the number of microlens contain in y and x direction [15] .
A new plenoptic camera configuration was proposed to provide a full resolution method was introduced to compensate the poor resolution in Ng method [18] . The full resolution method works by selecting pitch size under each element image to create a focused image, but this technique returns focused image containing artifacts making it unnatural [19] . The artifacts in the image are governed by choosing an accurate pitch size under specific element image therefore, depth information is necessary to illumine the artificts [15] . In addition, there have been good development recently [20] - [26] .
Introducing the depth information to full resolution method is to sustain natural looking photographic image. Therefore two approaches were presented in [19] to minimize artifacts. When selecting one patch size under each microlens and combining them together will only return one plane of the image. In other word the different patch size acts as refocusing feature, where different size patches look at a different plane. Furthermore, the depth estimating algorithm was applied to find the matching position of the same patch size from its neighboring microlens. This will remedy the artifacts problems in the images. Unfortunately this process is time consuming as it requires matching position of individual element images from its four neighboring element images. In this paper, a new approach is introduced to get full use of the viewpoint images by in-cooperating a new refocusing technique to improve the visual resolution.
3. The Proposed Method
The proposed method works by extracting the viewpoint images as illustrated in Figure 1. The viewpoint image is a low resolution orthography projection of rays from particular direction as shown in Figure 2. To generate high resolution image at particular plane it requires new interpolation technique. Thus, it involves up-sampling, shift and integration of viewpoints. This process will only generate one plane of high resolution image. To take one step further to generate all-in-focus image, all depth planes are needed to be obtained where later Michelson’s
Figure 1. Illustration of VP image extraction (For simplicity, assume there are only nine pixels under each microlens. Pixels in the same position under different microlenses represented by the same patern, are employed to form one VP).
Figure 2. One captured unidirectional 3D integral image is shown in the top left and one of the 67 extracted viewpoint image is illustrated on the next to top right hand side. On the left hand side we have the omnidirectional integral image and one extracted viewpoint image which also shown next to it.
contrast algorithm is applied on individual planes by window size selection. The highest contrast will return the focused and also the position of the shift as disparity value. The disparity value can be used later to generate the depth map of the scene to benefit coding, transmission, video games developing and interactive 3D display.
The contributions of this paper are as follows:
1) Development of new interpolation algorithms to preserve the resolution quality.
2) Presentation of a new refocusing method by changing the depth of field.
3) Presentation of an analysis of the depth of field of the integration process.
4) Development of a new algorithm to generate all-in-focus image by looking at different depth of plane and extract focused plane of the images.
5) Presentation of the depth information with point in space method.
4. Flowchart of the Proposed Method
In Figure 3, a detailed flowchart of the proposed method effectively shows the steps on how to acquire the all-in-focused image, depth map and refocusing image planes. The process of up-sampling, shift and integration of viewpoints enabling it to focus at particular depth plane with a given shift value after capturing. Therefore, at each shift’s value, the point is focused at particular depth plan. This allows it to change the depth of field by computational refocusing process at any desired plane. Furthermore, in obtaining all-in-focus image and depth information, a window size Michelson contrast estimation is applied on all depth planes and finally depth data of the objects are extracted by examining the point in space. At the focused point, the Michelson contracts estimation becomes to its highest and blur becomes to its lowest, whereas if the contracts decreases and blur increases, the depth plane is moving away for the object point. Therefore, the highest contrast with the lowest blur will return the object’s original position, meaning the highest contrast window from different depth planes will return an all-in-focus image.
4.1. Image Correction
An integral imaging system involves two processes recording and replaying. In the recording process an object is imaged through an array of lenses where each microlens captures a perspective 2D elemental image of the object from a specific angle. Thus the final captured image contains the intensity and directional information of the corresponding 3D scene in 2D form. The replay phase works in the reverse manner of the pickup, therefore the EIs are projected through the microlens arrays to optically reconstruct the 3D object at the same depth as the original object location.
Figure 3. Illustrates the flowchart of the proposed method.
The unidirectional integral image (UII) and omnidirectional integral image (OII) data are obtained by placing the micro-lens array in front of the camera sensor enabling each micro-lens to capture the 3D scene from different directions. The most common distortion caused by the lens, is, in this case barrel distortion that results from fitting the image in a smaller space. The squeezing of the image varies radially due to the design of the lenses making it more visually prominent at the corner and sides of the image [27] . This can be neglected in most of the image applications where the visual barrel effect cannot be seen.
However, in Viewpoint (VP) image extraction, it is important to correctly extract the same positioned pixels under every EI. Thus the image distortion needs to be corrected before proceeding to VP extraction. As shown in Figure 4(a), the VP image is extracted without correcting its distortion. This results in the final viewpoint image looking unnatural; by being unable to extract the same positioned pixel under different EI, therefore leaving out a portion of the scene and part of the object too. Where in Figure 4(b), VP image is extracted without barrel distortion.
4.2. Recording Setup
One of the setup scenes used in this paper is illustrated in Figure 5, where the objects are placed in a precisely measured distance from the camera. Each object are named “Target” with the recorded distance from the camera’s microlens, whereas Target 1, Target 2, Target 3 and Target 4 are respectively located in z1 = 3190 mm, z2 = 2000 mm, z3 = 1000 mm and z4 = 700 mm. In the recording process, 3D objects are captured in 2D format by microlens array placed in front of the camera sensor enabling each microlens captures the objects from a particular direction therefore, the outcome 3D image (integral image) holds the directional information of the scene. The integral image resolution obtained 5616 by 3744 pixels, consisting of 193 by 129 microlenses, with element

Figure 4. VP (a) pixel location (25, 25) under every EI extracted without correcting the barrel distortion and in (b) the same VP extracted without barrel distortion.
Figure 5. Scene setup.
image resolution of 29 by 29 pixels. The viewpoint image resolution is determined by the number of microlens contained in the recorded integral image, thus the resolution viewpoint image is 193 by 129 pixels.
4.3. Viewpoint Interpolation
A very attractive feature of integral image is a set of orthographic projections from various angles forming viewpoint images. However a major draw-back of the viewpoint approach leads to a significant resolution reduction on the final image. The resolution is meritoriously depended on the number of lenses and number of viewpoint, which gives the number of pixels places under each lens. This problem has been addressed in a variation of the plenoptic camera [15] , as its application has mainly been used in the refocusing of distant object near to the place of the lens array.
The new interpolation approach consists of up-sampling, shift and integration to generate spatially higher sampled images with unidirectional integral image (UII) and omnidirectional integral image (OII). In UII there is only one lenticular sheet along horizontal direction; whereas in OII there are lenses across horizontal direction and vertical direction.
The first step includes viewpoint extraction, where pixels are selected from each lens image in turn to form viewpoint at a resolution of 192 × 129 pixel. Then all VPs are up-sampled by N numbers in both horizontal and vertical direction before the shift and integration is applied. Up-sampled VPs are stacked adjacently in horizontal and top-to-bottom in vertical direction to form a 4D stack of images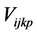 . Their subsequent shifting and integration results in obtaining a high resolution image. This operation can be expressed algebraically for omnidirectional integral image in a succinct form as shown in Equation (1).
. Their subsequent shifting and integration results in obtaining a high resolution image. This operation can be expressed algebraically for omnidirectional integral image in a succinct form as shown in Equation (1).
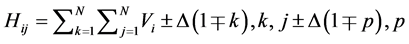 (1)
(1)
where Hij is the result of the integrated VP with coordinates i, j; k, p are the indexed number of VP ranging from 1 to N. Other parameters includes the shift parameter ∆, whose sign modifies the index i, j. V is the number of horizontal and vertical resolution EI; each VP is equal to the number of lenses multiplied by the up-sampling factor.
The amount of relative shift, in the images obtained by integration of VPs, determines the depth at which a sharp image is formed. This process is graphically demonstrated in Figure 6, in enhancing the resolution of rendered images when compared to standard interpolation of VP images. The result of the final rendered image produces a more photographic look around unfocused depth planes. Whereas adjusting the shift value changes the image plane in the final rendered image, as in some cases the focus is set to a distant object. As a result, the object that is close to the camera contains artifacts in the final rendered image. This is due to objects being at different depth. Therefore, enhancements were made to resolve the problem before the final image is produced. This is done by applying the quadratic interpolation on the VP images in the up-sampling process before shift and integration were applied. This approach solves the blackness on the final image resulting in smoother transition on unfocused areas of the plane.
The increase in resolution can be explained schematically in the one-dimensional example with two VPs represented by vectors; VPs integrating their pixel values with shown pixel coordinate within the circles as
Figure 6. Graphical representation of generating high resolution image.
shown in Figure 7. When shifted by 1 whole pixels = 2 subpixels, there is no resolution enhancement. This produces the same resolution image as integrating unshifted VPs. Red arrows represent up-sampled subpixels with same values and coordinates as their blue counterparts. With half a pixel shift = 1 subpixel, twice as many integration points are introduced. This is depicted by blue and red rays integrating their pixel values in the ellipses, resulting in a resolution enhanced image but at a slightly different depth in the z direction.
5. All-in-Focus
All-in-focus image is extracted by looking at all depth planes and returning areas with higher contrast and lower blur. The choice of one shift value returns one depth plane “in focus” with integration of VPs as mentioned above. Thus, a different shift value would correspond to a different depth plane. In other word the refusing is accomplished through the choice of shift value with the integration of VPs. The final all-in-focused image process is given by the following equations.
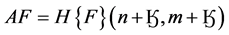 (2)
(2)
where,
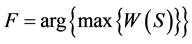 (3)
(3)
where,
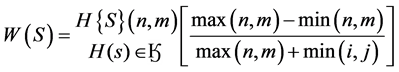 (4)
(4)
The H(S) n, m is the result of high resolution image whereas depth plane is depended on the number of shift (S),  At this point all depth planes are stored in H(S) n, m and their contrast values are calculated within the window block (Ӄ) in W(S) as shown in Equation (4). The maximum value of W(S) is selected and stored in F therefore; this indicates the depth plane where the objects are focused. Finally all-in-focused image is rendered in AF with window size (Ӄ) of H(F) n, m at higher contrast with lower blur as shown in Equations (2) (3).
At this point all depth planes are stored in H(S) n, m and their contrast values are calculated within the window block (Ӄ) in W(S) as shown in Equation (4). The maximum value of W(S) is selected and stored in F therefore; this indicates the depth plane where the objects are focused. Finally all-in-focused image is rendered in AF with window size (Ӄ) of H(F) n, m at higher contrast with lower blur as shown in Equations (2) (3).
6. Experimental Results
In the experiment, the outcome of the 3D image (OII) holds both the directional and positional information of
Figure 7. Schematicillustration of resolution increase.
the scene. A 5D canon camera is used with 50 mm main lens and 21-megapixel size image. The main lens is attached with a mountable extension tube on the camera to provide a flexible way of adjusting the distance between the main lens image plane to the microlenses and from the microlenses to the image sensor. The microlens focal length is 0.025 mm with pitch size of 0.9 mm. Furthermore, the main lens aperture is modified from circle to square to achieve a more effective way of using sensor space as the micro-lenses are square shaped.
The OII resolution is at 5616 by 3744 pixels, consisting of 193 by 129 micro-lenses, with EI resolution of 29 by 29 pixels. The VP resolution determined by the number of micro-lens contained in the recording, thus VP resolution is the same as the number of micro-lenses i.e. 193 by 129 pixels. The result of applying up-sampling, shift and integration leads to increasing the resolution of the final rendered image in comparison to the native approach using VPs interpolation. Both are compared with each other as it is very clear that native interpolation approach outputs the same resolution as its VP’s resolution (Figure 8). The up-sampling, shift and integration on the other hand, outputs images equal to VP resolution multiplied by the up-sampling factor.
The results of upsampling, shift and integration algorithm on the same OII, result in a significant increase in resolution and quality of the final images shown in Figure 9. In Figure 9(b), the Arri Media test chart is used to determine the effect in comparing both results. Note the “ARRI MEDIA” is successfully reconstructed with minimum blockening artifacts and noise, as a result a visual enhancement in the quality and resolution and quality. However, this process creates artifacts when the focusing at greater distance from the optical focal plane. In other word, the artifacts are more visible in the close up objects when the focus is on the far away distant as seen in Figure 9(a). Therefore, an enhancement was made to reduce the artifacts by having a smoother transition of VP’s pixels integrated to gain a more natural photographical looking image. The VPs are up-sampled by N times using quadratic interpolation this is to cure the problem artifacts that is seen in Figure 9(a). The final refocused image illustrates the resolution, as well as the visual quality by sustaining the natural photographic look in Figure 10.
All different image planes are obtained using upsampling, shift and integration as shown in Figure 11, later Michelson contrast algorithm is used on all the images planes to return all-in-focus image. The depth plane is dependent on the choice of shift value therefore; in the experiment the shift values are selected from 1 to 9, as the result of the different depth planes are extracted and shown in Figure 11. At each shift a different plane is “in focus” and depth z is also calculated at each shift value, where N = 49 viewpoints 7 × 7, f = 0.25 mm and n is the total number of viewpoints 841. The all-in-focus image is generated by using Michelson contrast algorithm applied on each depth plane with a window size of 20 × 20. Only the highest contrast values with lowest blur in the same window locations from the other nine planes are extracted, to identify windows where the object is in focused at a given shift plane. The highest contrast window’s shifts and lowest blur are recorded, which are later used in depth calculation as shown in Figure 12. Depth z is calculated by shift values S by Equation (2).
Figure 8. Up-sampling, shift and integration refocusing using 7 by 7 VPs: (a) shows the magnified part of the ARRI Media test chart with shift = 1; (b) focused at the toy with shift = 6. The final image is at resolution of 1344 × 903 pixels.
Figure 9. Native shift and integration refocusing is illustrated: (a) shows the magnified part of final refocusing image where the focus is at the object with shift = 6; (b) focused at the background with shift = 1: notice both (a) and (b) images are in poor quality containing blacking artifacts with significant noise that is seen more pixelated with naked eyes.
Figure 10. Up-sampling, shift and integration refocusing using 7 by 7 VPs: (a) shows the magnified part of the ARRI Media test chart; (b) shows the toy blurred, looking natural and no artifacts.
7. Conclusions
In this paper, a novel approach is introduced, which effectively refocuses low resolution orthographic images to form a high resolution image. Furthermore, a new interpolation approach is introduced to improve the visual quality of the final image. The final image looks more like a natural photography image without artifacts. The extraction of the all-in-focus image has been experimentally demonstrated. Depth information of the 3D object was also be extracted from the focused points.
Computational experiments are carried out to prove the enhancement on the resolution of the final image


Figure 11. 7 by 7 viewpoints are used in refocusing process to extract different depth plane in (a). In (b) where focus it on the background with z = 4.2 and (c) focuses at foreground with z = 0.71. In (d1) 7 by 7 VPs to focused at the background. (d2) Focused at the distant 100mm. (d3) using 5 by 5 VPs focused at background. (d4) Focused at 1 meter from the microlens array.

Figure 12. Image is displayed on the left (a) and depth information is on the right (b).
using the viewpoint method and also to improve visual quality using new interpolation approach after refocusing. The experiments are performed on both, unidirectional and omnidirectional images resulting in a successful outcome of an improving on the final image. The new all-in-focus with depth information algorithm is also successful in extracting the all-in-focus image with exceptional depth information.
Cite this paper
Obaidullah Abdul Fatah,Peter Lanigan,Amar Aggoun,Mohammad Rafiq Swash, (2016) Digital Refocusing: All-in-Focus Image Rendering Based on Holoscopic 3D Camera. Journal of Computer and Communications,04,24-35. doi: 10.4236/jcc.2016.46003
References
- 1. Okoshi, T. (1976) Three Dimensional Imaging Techniques. Academic Press, xi.
- 2. Park, J.-H., Hong, K. and Lee, B. (2009) Recent Progress in Three-Dimensional Information Processing Based on Integral Imaging. Applied Optics, 48, H77-H94.
http://dx.doi.org/10.1364/AO.48.000H77 - 3. Lee, J.-H., Ko, J.-H., Lee, K.J., Jang, J.-H. and Kim, E.-S. (2004) Implementation of Stereo Camera-Based Automatic Unmanned Ground Vehicle System for Adaptive Target Detection. Intelligent Robots and Computer Vision XXII: Algorithms, Techniques, and Active Vision, Philadelphia, 25 October 2004, 188-197.
http://dx.doi.org/10.1117/12.573829 - 4. Gabor, D. (1948) A New Microscope Principle. Nature, 161, 777.
http://dx.doi.org/10.1038/161777a0 - 5. Lippmann, G. (1908) La Photographie Integrale. Comtes Rendus, Academie des Sciences, 146, 446-451.
- 6. Aggoun, A., Tsekleves, E., Swash, M.R., Zarpalas, D., Dimou, A., Daras, P., Nunes, P. and Soares, L.D. (2013) Immersive 3D Holoscopic Video System. IEEE Multimedia Special Issue: 3D Imaging Techniques and Multimedia Applications, 20, 28-37.
- 7. Lippmann, G. (1908) Epreuvesreversiblesdonnant la sensation du relief. Journal of Physics, 7, 821-825.
- 8. Ijsselsteijn, W., de Ridder, H. and Vliegen, J. (2000) Effects of Stereoscopic Filming Parameters and Display Duration on the Subjective Assessment of Eye Strain. Proceedings of the SPIE, Stereoscopic Displays and Virtual Reality Systems VII, 3957, 12-22.
http://dx.doi.org/10.1117/12.384448 - 9. Martnez-Cuenca, R., Navarro, H., Saavedra, G., Javidi, B. and Martinez-Corral, M. (2007) Enhanced Viewing-Angle Integral Imaging by Multiple-Axis Telecentric Relay System. Optics Express, 15, 16255-16260.
http://dx.doi.org/10.1364/OE.15.016255 - 10. Kim, Y., Park, J.-H., Min, S.-W., Jung, S., Choi, H. and Lee, B. (2005) Wide-Viewing-Angle Integral Three-Dimensional Imaging System by Curving a Screen and a Lens Array. Applied Optics, 44, 546-552.
http://dx.doi.org/10.1364/AO.44.000546 - 11. Park, J.-H., Jung, S., Choi, H. and Lee, B. (2002) Viewing-Angle-Enhanced Integral Imaging by Elemental Image Resizing and Elemental Lens Switching. Applied Optics, 41, 6875-6883.
http://dx.doi.org/10.1364/AO.41.006875 - 12. Zarpalas, D., Fotiadou, E., Biperis, I. and Daras, P. (2012) Anchoring Graph Cuts towards Accurate Depth Estimation in Integral Images. Journal of Display Technology, 8, 405-417.
- 13. Ko, J.-H. and Kim, E.-S. (2006) Stereoscopic Video Surveillance System for Detection of Target’s 3D Location Coordinates and Moving Trajectories. Optics Communications, 191, 100-107.
http://dx.doi.org/10.1016/j.optcom.2006.04.020 - 14. Manolache, S., Kung, S.Y., McCormick, M. and Aggoun, A. (2006) 3D-Object Space Reconstruction from Planar Recorded Data of 3D-Integral Images. Journal of VLSI Signal Processing Systems, 35, 5-18.
- 15. NGR (2006) Digital Light Field Photography. PhD Thesis, Stanford University, Stanford.
- 16. Fife, K., Gamal, A.E. and Wong, H.-S.P. (2008) A 3MPixel Multi-Aperture Image Sensor with 0.7 μm Pixels in 0.11μm CMOS. 2008 IEEE International Solid-State Circuits Conference—Digest of Technical Papers, San Francisco, 3-7 February 2008, 48-594.
http://dx.doi.org/10.1109/ISSCC.2008.4523050 - 17. Lumsdaine, A. and Georgiev, T. (2008) Full Resolution Lightfield Rendering. Technical Report, Adobe Systems, January.
- 18. Georgiev, T. and Lumsdaine, A. (2010) Focused Plenoptic Camera and Rendering. Journal of Electronic Imaging, 19, Article ID: 021106.
- 19. Lumsdaine, A. and Georgiev, T. (2009) The Focused Plenoptic Camera. Proceedings of the International Conference on Computational Photography, San Francisco, 16-17 April 2009, 1-8.
http://dx.doi.org/10.1109/iccphot.2009.5559008 - 20. Swash, M.R., Fernández, J.C., Aggoun, A., Abdulfatah, O., Li, B. and Tsekleves, E. (2014) Referenced Based Holoscopic 3D Camera Aperture Stitching For Widening the Overall Viewing Angle. 3DTV-CON in Pursuit of Next Generation 3D Display, Budapest, 2-4 July 2014, 1-3.
- 21. Alazawi, E., Abbod, M., Aggoun, A., Swash, M.R. and Abdulfatah, O. (2014) Super Depth-Map Rendering by Converting Holoscopic Viewpoint to Perspective Projection. 3DTV-CON in Pursuit of Next Generation 3D Display, Budapest, 2-4 July 2014, 1-4.
- 22. Swash, M.R., Abdulfatah, O., Alazawi, E., Kalganova, T. and Cosmas, J. (2014) Adopting Multiview Pixel Mapping for Enhancing Quality of Holoscopic 3D Scene in Parallax Barriers Based Holoscopic 3D Displays. IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, Beijing, 25-27 June 2014, 1-4.
http://dx.doi.org/10.1109/bmsb.2014.6873560 - 23. Alazawi, E., Aggoun, A., Cosmas, J., Swash, M.R., Abdulfatah, O. and Abbod, M. (2014) 3D-Interactive-Depth Generation and Object Segmentation from Holoscopic Image. IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, Beijing, 25-27 June 2014, 1-5.
http://dx.doi.org/10.1109/BMSB.2014.6873494 - 24. Swash, M.R., Aggoun, A., Abdulfatah, O., Li, B., Jacome, J.C., Alazawi, E. and Tsekleves, E. (2013) Pre-Processing of Holoscopic 3D Image for Autostereoscopic 3D Display. 5th International Conference on 3D Imaging (IC3D), Liege, 3-5 December 2013, 1-5.
http://dx.doi.org/10.1109/ic3d.2013.6732100 - 25. Swash, M.R., Aggoun, A., Abdulfatah, O., Alazawi, E. and Tsekleves, E. (2013) Distributed Pixel Mapping for Refining Dark Areas in Parallax Barriers Based Holoscopic 3D Displays. 5th International Conference on 3D Imaging (IC3D), Liege, 3-5 December 2013, 1-4.
http://dx.doi.org/10.1109/ic3d.2013.6732101 - 26. Swash, M.R., Aggoun, A., Abdulfatah, O., Li, B., Fernández, J.C., Alazawi, E. and Tsekleves, E. (2013) Moiré-Free Full Parallax Holoscopic 3D Display Based on Cross-Lenticular. 3DTV-CON: Vision beyond Depth AECC, Aberdeen, 7-9 October 2013.
- 27. Tian, H., Srikanthan, T., Asari, K.V. and Lam, S. (2002) Study on the Effect of Object to Camera Distance on Polynomial Expansion Coefficients in Barrel Distortion Correction. Proceedings of 5th IEEE Southwest Symposium on Image Analysis and Interpretation, Sante Fe, 7-9 April 2002, 255-259.
http://dx.doi.org/10.1109/IAI.2002.999928











