Journal of Computer and Communications
Vol.03 No.10(2015), Article ID:60725,8 pages
10.4236/jcc.2015.310003
Image Denoising Combining the P-M Model and the LLT Model
Qian Yang
School of Mathematical Science, University of Electronic Science & Technology of China, Chengdu, China
Email: dianzikedashuxue@126.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 May 2015; accepted 26 October 2015; published 29 October 2015
ABSTRACT
In this paper, we present a noise removal technique by combining the P-M model with the LLT model. The combined technique takes full use of the advantage of both filters which is able to preserve edges and simultaneously overcomes the staircase effect. We use a weighting function in our model, and compare this model with the P-M model as well as other fourth-order functional both in theory and numerical experiment.
Keywords:
P-M Model, LLT Model, Fourth-Order PDEs, Combination, Image Denoising

1. Introduction
In image processing, the methods based on variation and PDEs play an important role. In recent years, many scholars have done a lot of research in this respect, and many good results have been achieved on image such as enhancing, sharping, and denoising images. See for instance [1] -[7] . The total variation minimization introduced by Rudin, Osher, and Fatemi [6] is the most significant of such methods. But now, one will consider the following more general functional
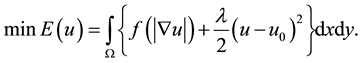 (1)
(1)
By using the functional variation principle to figure out the corresponding Euler-Lagrange equation, we can find the solution of Equation (1) to approach the original image. These second order partial differential equations (PDEs) models [8] - [10] are shown to be very useful in image denoising, restoration, inpainting, etc. Mean- while, most of the second-order models have a drawback; the drawback is that these models can produce the blocky effects. The authors in [11] - [15] also put forward a variety of fourth-order PDEs models. In the domain with a smooth changed in the intensity value, most of second-order models have a tendency to converge to a piecewise constant image, while the fourth-order PDEs models converge to a piecewise planar image. In this regions, the gradient of the fourth-order PDEs maintains a constant (not 0); thus it reduces that image would not have the extra edge. However, many fourth-order PDEs models have some common shortcomings: blurring the image feature to some extent and producing speckle. Our principal contribution of this paper is to produce a new solution by taking the best from the second-order and the fourth-order PDEs models by a convex combination. A weighting function is used in an iterative way to generate a new model. This weighing function is used to balance the relative weights of the two methods. Our intention is to improve the quality of the recovered image, such as suppressing the noise, overcoming the blocky effect and preserving the sharp edges. This paper is organized as follows: we give a brief description of the classic second-order PDEs model (the P-M model) and fourth-order PDEs model (the LLT model), and will give a method to find out the solution of the scale parameter in Section 2. In Section 3, we consider the convex combination of the above two models. Implementation details are given in Section 4. In Section 5, we give the numerical experiments along with comparisons among the P-M model and various fourth-order models. Finally, we conclude with a brief discussion in Section 6.
2. Prior Work
2.1. A Typical Second-Order Model: The P-M Model
The P-M model has a good performance in many details and it is the origin of the other models. It is well known that the model represented by Perona and Malik [10] is derived from the following functional,
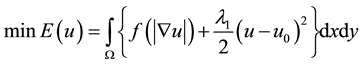 (2)
(2)
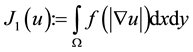 (3)
(3)
where 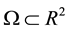 is an open, bounded and connected domain with Lipschitz boundary,
is an open, bounded and connected domain with Lipschitz boundary, 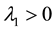 is a parameter that balances the relative weights of the two terms, and some times, it can also be interpreted as a Lagrange multiplier. u is taken in an appropriate Sobolev space
is a parameter that balances the relative weights of the two terms, and some times, it can also be interpreted as a Lagrange multiplier. u is taken in an appropriate Sobolev space 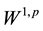 on the space
on the space 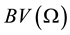 of function with bounded variation on
of function with bounded variation on 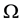 and f is a function of the magnitude of u, we know that
and f is a function of the magnitude of u, we know that 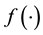 is a non negative monotonically in-
is a non negative monotonically in-
creasing function. 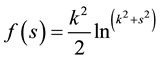 defined by Perona and Malik. Under these conditions, Perona and Malik
defined by Perona and Malik. Under these conditions, Perona and Malik
minimized the energy functional (2), thus and obtained the following equation
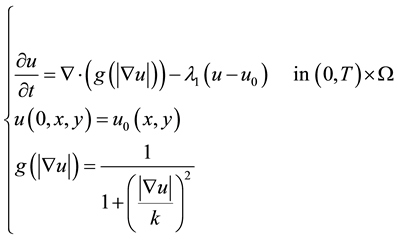 (4)
(4)
here g is the diffusion coefficient, and g(・) is a non negative monotonically decreasing function with g(0) = 1 as
well as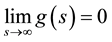 ,
, 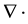 and
and 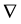 denote the divergence and the gradient. one can get a result that the inten-
denote the divergence and the gradient. one can get a result that the inten-
sity of the level image is the global minima of the energy functional from (2) and (4). One should notice that there are many fast methods to minimize (2) such as [14] .
2.2. A Fourth-Order PDEs Model
The P-M model can remove the noise, at the same time it will produce the staircase effect, while the fourth-order model can remove the noise and will not generate the blocky effect. Since the Laplacian of the image at a pixel is zero only if the image is planar in its neighborhood, there are many fourth-order PDEs models attempt to remove noise by approaching piecewise planar image. Piecewise planar image looks more natural than step images which anisotropic diffusion, in other word, the fourth-order model will not produce the staircasing effect. It also is a strength of the LLT model. This model is put forward by Lysaker and Tai et al. In [4] :
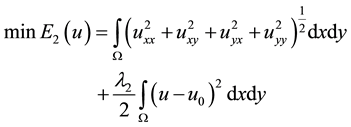 (5)
(5)
where the parameter λ2 > 0 which balances the relative weights of the two terms. This model is called the LLT
model. For simplicity we introduce the notation 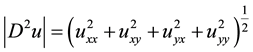 and denote (5) by
and denote (5) by


Through the calculation of this variation, the gradient descent PDE of the minimization is

To avoid singularities in the above systems, we replace 



Since the problem is convex, the steady state solution of the gradient descent PDE (9) is the minimizer of the energy functional. Numerical experiments show that the LLT model is able to greatly supress the staircase effect, but blur image and produce the speckle effect.
2.3. Solving Scale Parameters
In order to find an appropriate scale parameter in our approach, firstly, we will give the specific calculation method [4] [16] . As commonly done, we can also view (2), (6) as a constrained problems:


where 






These equations give us some dynamic values, which appear to converge as
3. Convex Combination-Based Second and Fourth Order Diffusion
In Section 2, the P-M model and the LLT model are presented in front of us, and in this section, we will combine these models with a weighting function. The image enhancement techniques for image deboising is a good approach to combine the advantages of the second-order PDEs method and the fourth-order PDEs method, thus has been popular, such as [17] [18] method. Now, we will give a new combination model. Firstly, we use the notation v and u to distinguish the solution of (4) and (8), respectively. One can apply variational principle to minimize the energy functional which is put forward by Perona et al., and get the steady-state solution of the nonlinear diffusion process

And the LLT model as follows
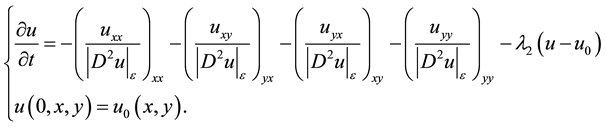
Set Ω is a rectangular domain, 


where 

And the initial condition is:
To some extent, these two models are able to suppress the noise, but it is well known that the first model is prone to massive effect, while the second model is tend to blur images and produce the speckles. Both methods have their pros and cons depending on the character of the image interest. We should find out a way for demonstrating the merits of these two models, at the same time, the shortcoming is suppressed by adjusting the parameter. Considering (14) and (15), we try to create a new model by a convex combination 





of different ways. one can find that when 
paper, we find out a α = 0.625 by repeated experiments, it works fine. As for more detailed algorithms, we will give them in the following.
4. Difference Scheme
As in [19] , one can minimize (4) and (8), respectively, by using evolution Equations (14) and (15), and one can discrete (14) with difference scheme, the expression as follows: first, let ∆x and ∆y be the square lattice sizes for the x and y variables, ∆t > 0 be the artificial time step in the descent direction. And we denoted 





where 
Note that N, S, E, W represent the North, the South, the East and the West, respectively. And the symbol σ indicates 4-nearest-neighbors differences:
And the diffusion coefficient 
Similarly, we can obtain the LLT discrete form: firstly, see [4] , we can get
These are discrete format of the P-M model and the LLT, but our focus points are the following:
Here, the value of α is 0.625, it is a preferred value of α. When α is different, the effect of image denoising is distinct. In the following numerical experiments, it will prove that a combination model is effective and accurate.
5. Numerical Experiments
In this section, we will present numerical results obtained by applying our proposed model to image denoising. For comparison, we also present some results from application of the P-M model (14) and the LLT model (15) to the same images. From the result of experiment, we will utilize the pictures to verify these models, especially demonstrate the advantages of the convex combining model: the new model can reduce the blocky effects and avoid leaving the speckle artifacts. The following two classical single PDE schemes are:
(a) The model proposed by Perona and Malik [10]
(b) Lysaker and Tai et al. raised such model [12]
Note that, to avoid singular in the LLT model, we utilize the above expression. The contrast parameter k > 0 can be chosen in a variety of ways. Further, we proposed our model to compare with the above models.
(c) Convex combination of the above two models.
From the expression, we know that our model is built on the basis of two classical models. Our model is more natural, and the effect is good in comparison with the model which is obtained by an energy functional that contains gradient functions and Laplace functions. Our experimental pictures are 256 × 256 sized gray-scale image Lena. We consider the noisy image f = u + n where u is the original image, and the n is a white Gaussian noise with the expectation zero and standard deviation σ. In Figure 1, we show some results on Lena image. Top left is the original image, Top medium is a noisy Lena gray scale image with the white Gaussian noise with standard deviation σ = 15. Top right is the denoised image u by our new model with λ1 = 1, λ2 = 1, and bottom left is the denoised images u by the convex combination model with λ1 = 0.3, λ2 = 0.5, another two sets of data are λ1 = 0.1, λ2 = 0.2 and λ1 = 0.05, λ2 = 0.1, respectively. From these data, we can know that when the other parameters are unchanged, the near the parameter λ1 and λ2 approximate to 0.5, the better the result. The SNR of the top right picture is 20.0640 and the PSNR value is 26.6707, similarly, from bottom left picture to bottom right picture, we get that the SNR values are 23.0891, 22.7871, 20.9781, respectively and the PSNR values are 29.6958, 29.3938 and 27.5848, but finally we will found that the near the parameter λ1 and λ2 approximate to 0.5, the speckles of the image is more obvious. On the whole, one can find out that λ1 = 0.1 and λ2 = 0.2 is suitable.
Figure 2 shows a comparative result for the noisy Lena gray scale image (σ = 15) with the classical P-M model and the LLT model. In these pictures, we can see that the convex combination model presents a more distinct image than the other models. The new model (α = 0.625) avoids the staircasing artifacts associate with the P-M model, at the same time, it prevents that the edges are blurred. Figure 3 shows a comparative result for a small part of the Lena image (σ = 15). In this group of images, we will see that the P-M model appears obvious blocky effect and the LLT model leaves the speckle artifacts. Our proposed model can avoid the staircase and the speckle effect while removing noise. Note that we use signal to noise (SNR) [5] [17] [20] as means of judging performance:
Figure 1. Top left: The original image u, top medium: a noisy image f with a white Gaussian noise (σ = 15), top right: the denoised Lena image by the convex combination model with








Figure 2. Comparison of denoising results on noisy Lena image. Top left: the noisy image with a white Gaussian noise σ = 15, top right: the denoised image u by The LLT model, with PSNR = 29:2871, bottom left: the denoised image u by the PM model with PSNR = 27:9767, bottom right: the denoised image u by the convex combination model with PSNR = 29:4037.
(1)
where u is the original image, f is the recovery and f is its mean value.
(2) Signal to noise ratio (PSNR) is defined by:
where 

(3)
where f denotes the denoised image and u denotes the original image.


Figure 3. A small portion of the Lena image is shown to better emphasize disparties in the smooth surface.
Table 1. SNR and PSNR comparison of various models for the Lena image.
In Table 1, we give the comparison results of the SNR and the PSNR using these three models. As can be seen, the convex combination model performs well for a variety of images (Lena, the small part of the Lena).
6. Conclusion
This paper proposes a convex combination model by the P-M model and the LLT model, and α = 0.625 is found to balance these two models. Numerical results represent the competitive performance of the new model, for noise removal while maintaining the jump discontinues better, and suppressing the speckles.
Cite this paper
QianYang, (2015) Image Denoising Combining the P-M Model and the LLT Model. Journal of Computer and Communications,03,22-30. doi: 10.4236/jcc.2015.310003
References
- 1. Catt, F., Lions, P., Morel, J. and Coll, T. (1992) Image Selective Smoothing and Edge Detection by Nonlinear Diffusion. SIAM Journal on Numerical Analysis, 29, 182-193.
http://dx.doi.org/10.1137/0729012 - 2. Duran, J., Buades, A., Coll, B., et al. (2014) A Nonlocal Variational Model for Pansharpening Image Fusion. SIAM Journal on Imaging Sciences, 7, 761-796.
http://dx.doi.org/10.1137/130928625 - 3. Jin, Y., Jost, J. and Wang, G. (2004) A New Nonlocal Model for Image Denoising. Journal of Mathematical Imaging and Vision, 48, 93-105.
http://dx.doi.org/10.1007/s10851-012-0395-2 - 4. Lysaker, M., Lundervold, A. and Tai, X.C. (2003) Noise Removal Using Fourth-Order Partial Differential Equation with Applications to Medical Magnetic Resonance Images in Space and Time. IEEE Transactions on Image Processing, 12, 1579-1590.
http://dx.doi.org/10.1109/TIP.2003.819229 - 5. Lieu, L.H. and Vese, L.A. (2008) Image Restoration and Decomposition via Bounded Total Variation and Negative Hilbert-Sobolev Spaces. Applied Mathematics & Optimization, 58, 167-193.
http://dx.doi.org/10.1007/s00245-008-9047-8 - 6. Rudin, L., Osher, S. and Fatemi, E. (1992) Nonlinear Total Variation Based Noise Removal Algorithms. Physica D, 60, 259-268.
http://dx.doi.org/10.1016/0167-2789(92)90242-F - 7. Surya Prasath, V.B. and Vorotnikov, D. (2004) On a System of Adaptive Coupled PDEs for Image Restoration. Journal of Mathematical Imaging and Vision, 48, 35-52.
http://dx.doi.org/10.1007/s10851-012-0386-3 - 8. Alvarez, L., Lions, P. and Morel, J. (1992) Image Selective Smoothing and Edge Detection by Nonlinear Diffusion. II. SIAM Journal on Numerical Analysis, 29, 845-866.
http://dx.doi.org/10.1137/0729052 - 9. Jin, Y., Jost, J. and Wang, G. (2012) A Nonlocal Version of the Osher-Sol-Vese Model. Journal of Mathematical Imaging and Vision, 44, 99-113.
http://dx.doi.org/10.1007/s10851-011-0313-z - 10. Perona, P. and Malik, J. (1990) Scale-Space and Edge Detection Using Anisotropic Diffusion. IEEE Transaction on Pattern Analysis and Machine Intelligence, 12, 629-639.
http://dx.doi.org/10.1109/34.56205 - 11. Kim, S. and Lim, H. (2009) Fourth-Order Partial Differential Equation for Effective Image Denoisng. 7th Mississippi State-UAB Conference on Differential Equation and Computational Simulation. Electronic Journal of Differential Equations, 17, 107-121.
- 12. Liu, X.W., Huang, L.H. and Guo, Z.Y. (2011) Adaptive Fourth-Order Partial Differential Equation Filter for Image Denoising. Applied Mathematics Letters, 24, 1282-1288.
http://dx.doi.org/10.1016/j.aml.2011.01.028 - 13. Wang, L.Q., Xiao, L., Huang, L.L. and Wei, Z.H. (2011) Nonlocal Total Variation Based Speckle Noise Removal Method for Ultrasound Image. 2011 4th International Congress on Image and Signal Processing (CISP), 2, 709-713.
http://dx.doi.org/10.1109/cisp.2011.6100293 - 14. You, Y.L. and Kaveh, M. (2000) Fourth-Order Partial Differential Equation for Noise Removal. IEEE Transaction on Image Processing, 9, 1723-1731.
http://dx.doi.org/10.1109/83.869184 - 15. Zhou, G.X., Zhang, Q.S. and Tan, X.H. (2011) Image Enhancement and Denoising by Forward and Backward Fourth Order Partial Differential Equations. In: Lin, S. and Huang, X., Eds., Advances in Computer Science, Environment, Ecoinformatics, and Education, Springer-Verlag, Berlin, 514-519.
http://dx.doi.org/10.1007/978-3-642-23339-5_94 - 16. Gilboa, G. and Osher, S. (2007) Nonlocal Linear Image Regularization and Supervised Segmentation. Multiscale Modeling & Simulation, 6, 595-630.
http://dx.doi.org/10.1137/060669358 - 17. Liu, T.H. and Xiang, Z.Y. (2013) Imaging Restoration Combing the Second-Order and Fourth-Order PDEs. Mathematical Problems in Engineering, 2013, Article ID: 743891.
- 18. Wang, H.B., Wang, Y.Q. and Ren, W.Q. (2012) Image Denoising Using Anisotropic Second and Fourth Order Diffusions Based on Gradient Vector Convolution. ComSIS, 9, 1493-1511.
http://dx.doi.org/10.2298/CSIS120219060W - 19. Li, X.P. and Chen, T.W. (1994) Nonlinear Diffusion with Multiple Edginess Thresholds. Pattern Recognition, 27, 1029-1037.
http://dx.doi.org/10.1016/0031-3203(94)90142-2 - 20. Lou, Y.F., Zhang, X.Q., Osher, S. and Bertozzi, A. (2010) Image Recovery via Nonlocal Operators. Journal of Scientific Computing, 42, 185-197.
http://dx.doi.org/10.1007/s10915-009-9320-2





























