Journal of Computer and Communications
Vol.03 No.04(2015), Article ID:55482,6 pages
10.4236/jcc.2015.34003
Improved Non-Local Means Algorithm for Image Denoising
Lingli Huang
School of Mathematical Sciences, University of Electronic Science & Technology of China, Chengdu, China
Email: huanglingli910213@163.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 March 2015; accepted 9 April 2015; published 10 April 2015
ABSTRACT
Image denoising technology is one of the forelands in the field of computer graphic and computer vision. Non-local means method is one of the great performing methods which arouse tremendous research. In this paper, an improved weighted non-local means algorithm for image denoising is proposed. The non-local means denoising method replaces each pixel by the weighted average of pixels with the surrounding neighborhoods. The proposed method evaluates on testing images with various levels noise. Experimental results show that the algorithm improves the denoising performance.
Keywords:
Image Denoising, Non-Local Means, Gaussian Noise

1. Introduction
Image denoising [1] is a hot research issue in the field of digital image processing. Image denoising is very important on guaranteeing the effectiveness and robustness of other image processing algorithms in the industry image process procedures, such as image registration, image segmentation. So image denoising has attracted more and more attentions from many researchers and many denoising methods have been proposed, such as PDE-based approaches [2] - [4] , transform-domain methods [5] , the Gaussian smoothing model, the neighborhood filtering [6] , the empirical Wiener filters [7] and the wavelet thresholding method [8] .
It has proved that the spatial domain smoothing is effective to remove the additive Gaussian noise in the noisy image. The key idea is to replace the intensity value of each pixel by a weighted average of all intensity values of its neighborhood. The weight can be computed via the Gaussian filter or the box filter. The basic idea of the Gaussian filter is that the value of the pixels of its neighborhood is given different weighting which is defined by a spatial Gaussian distribution. In 1998, Manduchi and Tomasi proposed a bilateral filter and used it to compute the weighting function.
Buades, Coll and Morel proposed non-local means algorithm [9] [10] . Buades proposed a new non-local means algorithm in 2011 [11] . Moreover, they proved that the algorithm had a superior denoising performance than other methods, such as the Means filter, the Bilateral filtering. Many researches based on NLM have been done in recent years [12] . In [12] , it used a small set of predetermined filters and reduced the influence of less- related areasto denoise a pixel. But the weight is computed from the high-dimensional vectors. Moreover by using the summed square image, the paper [13] reduced computational cost, but the weight was still computed in the high-dimensional space. The methods above-mentioned are based on image neighborhoods and they are the important methods to denoise the image.
The non-local means denoising method replaced each pixel in the noisy image by the weighted average of pixels with related surrounding neighborhoods. The weighting function is determined by the similarity between neighborhoods. Many papers have introduced a more detailed analysis on the non-local means algorithm.
The most important problem is to determine the weighting function. In this paper, it proposes a different weighting function and gets an improved non-local means algorithm for image denoising. This paper uses a different weighting function to compute the weight and makes some experiments to compare the different weighting function against the original function, and it is shown that the improved non-local algorithm outperforms the original non-local means method.
The structure of this paper is as follows. In Section 1, it introduces the development of the non-local means algorithm. In Section 2, this paper introduces the non-local means algorithm. Section 3 proposes an improved non-local means method. In Section 4, experimental results of test images are proposed to compare with the other non-local means methods and conclusions follow in Section 5.
2. Nonlocal Means Algorithm
In this section, a brief review of standard non-local means method is introduced.
In the original non-local means algorithm, the method first computes the similarity between the window centered on a pixel and the window centered on other pixels in the noisy image. The method uses the similarity to compute the weighting function.
In this paper, the image is assumed to be corrupted by Gaussian white noise with zero-mean and variance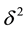 . The observation image model can be considered as
. The observation image model can be considered as
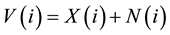 . (1)
. (1)
Given a discrete noisy image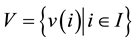 , where I represents the image domain. For a pixel i, the estimated value is computed as
, where I represents the image domain. For a pixel i, the estimated value is computed as
 , (2)
, (2)
where  is determined by the similarity between the pixel i and j, and satisfy the usual conditions
is determined by the similarity between the pixel i and j, and satisfy the usual conditions
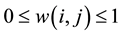 and
and .
. 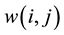 is defined as
is defined as
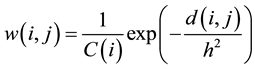 , (3)
, (3)
where  is the normalizing constant
is the normalizing constant
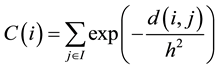 ,
,
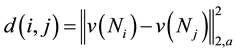 ,
,
and 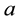 is the standard deviation of the Gaussian kernel, h is the decay parameter, it controls the decay of the exponential function.
is the standard deviation of the Gaussian kernel, h is the decay parameter, it controls the decay of the exponential function. 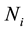 denotes a square neighborhood of fixed size
denotes a square neighborhood of fixed size 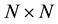 centered at pixel i, and
centered at pixel i, and  denotes the intensity gray values of
denotes the intensity gray values of 

The non-local means algorithm has attracted much attention and more and more researchers pay attention to the weighting function. The original non-local means algorithm uses the exponential decaying function as a weighting function. The problem of measuring the similarity between pixels is a hot issue in many fields, such as the image processing, computer vision and machine learning.
This paper testes and estimates the performance of the non-local algorithm using our proposed weighting function for the similarity measurement instead of the exponential function. The result shows that the proposed weighting function in non-local means algorithm will lead to an efficient implementation of this algorithm.
3. Improvements in Proposed Method
In the original non-local means method, in order to make the neighborhoods with similar structure receive a larger weight, it uses the exponential function. The paper [13] proposed many kernel functions, such as Turkey bi-weight function is expressed as

The paper [14] introduced several new kernel functions to be further incorporated into the conventional nonlocal filtering framework to develop new filters. Moreover the paper analyzed each function and conduct some experiments to demonstrate it.
This paper gets a new weighting function by analyzing the exponential function and Turkey bi-weight

where
Moreover the paper [15] introduces that bilateral filtering makes the intensity value at each pixel in an image replaced by a weighted average of intensity values from nearby pixels. Crucially, the weights depend not only on Euclidean distance of pixels, but also on the radiometric differences (e.g. range differences, such as color intensity, depth distance, etc.). This preserves sharp edges by systematically looping through each pixel and adjusting weights to the adjacent pixels accordingly. For a pixel i, the estimated value is computed as



where 



Through the introduction of the above problem, this paper gets an improved weighting function

where
4. Experimental Results
In this section, it presents some of the results obtained by the proposed method and compares them with the non-local means denoising method. From the experimental results, the new model presented in this paper can performance better than the non-local means denoising method (Figures 1-6).
Our examples are 256 × 256 sized gray-scale image Lena and Cameraman. Their degraded version is corrupted by white random Gaussian noise with standard deviation 10. The simulations used a 5 × 5 window for weight calculation and 7 × 7 window for neighborhood pre-classification. In order to speed up the simulation,

Figure 1. Recovered results via the original non-local means algorithm. (a) Original image; (b) Noisy image; (c) Filtered image; (d) Residuals.

Figure 2. Recovered results via the l non-local means algorithm in paper [11] . (a) Original image; (b) Noisy image; (c) Filtered image; (d) Residuals.

Figure 3. Recovered results via our proposed improved non-local means algorithm. (a) Original image; (b) Noisy image; (c) Filtered image; (d) Residuals.

Figure 4. Partially enlarged results are displayed via the original non-local means algorithm. (a) Original image; (b) Noisy image; (c) Filtered image; (d) Residuals.

Figure 5. Partially enlarged results are displayed via the l non-local means algorithm in paper [11] . (a) Original image; (b) Noisy image; (c) Filtered image; (d) Residuals.

Figure 6. Partially enlarged results are displayed via our proposed improved non-local means algorithm. (a) Original image; (b) Noisy image; (c) Filtered image; (d) Residuals.
this paper restrict the search for similar neighborhoods to a 21 × 21 window. The radius of 


The paper presents the above-mentioned zoomed-in local results to better understand the behavior of the proposed method in local regions, especially in regions with discontinuities.
A small part of the Lena image is shown in Figures 4-6. It is clear that our proposed model can avoid the staircase and the speckle artifacts while removing the noise.
Moreover the figure displays the method noise for the standard image Lena, it can be seen that the above- mentioned figures that the improved non-local means method noise does not present any noticeable geometrical structures.
The restoration quality can be quantitatively measured by the signal-to-noiseratio (SNR) and the peak signal- to-noise ratio (PSNR), which are defined as
Table 1. Performance comparison of Lena image with various levels of noise.
Table 2. Performance comparison of partially enlarged Lena image with various levels of noise.
respectively, where h denotes the compared image, g is the original image, and the unit of SNR (PSNR) is decibel (dB).
In Table 1 and Table 2, it gives the comparison of the PSNR for the above-mentioned figures, which shows that our method has the better PSNR than the original non-local means method. This paper denotes the method in [10] as ONLM and it denotes the method in [11] as CNLM.
5. Conclusion
This paper proposes an improved non-local means method. The method uses a new weight kernel for preprocessing. The paper has tested our algorithm on images consisting of edges and smooth regions. Some features of the images are well preserved even better than the classical non-local means technique. The comparisons made for the denoising images from various denoising techniques are presented. This new proposal considerably increases the power of denoising and one can say that the proposed approach achieved the worthy level of pertinence. From these experimental results, this paper observes that the proposed method is able to preserve edges in the Lena image with high details and gets a higher PSNR, as well as better visual quality.
References
- Liu, C., Szeliski, R., Kang, S.B., et al. (2008) Freeman, Automatic Estimation and Removal of Noise from a Single Image. IEEE Transactions on Pattern Analysis and Machine Intelligence, 30, 299-314. http://dx.doi.org/10.1109/TPAMI.2007.1176
- Rudin, L., Osher, S. and Fatemi, E. (1992) Nonlinear Total Variation Based Noise Removal Algorithms. Physica D, 60, 259-268. http://dx.doi.org/10.1016/0167-2789(92)90242-F
- Perona, P. and Mlik, J. (1990) Scale-Space and Edge Detection Using Anisotropic Diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12, 629-639. http://dx.doi.org/10.1109/34.56205
- Bayram, I. and Kamasak, M.E. (2012) Directional Total Variation. IEEE Signal Processing Letters, 12, 781-784. http://dx.doi.org/10.1109/LSP.2012.2220349
- Portilla, J., Strela, V., Wainwright, M.J. and Simoncelli, E.P. (2003) Imagedenoising Using Scale Mixtures of Gaussians in the Wavelet Domain. IEEE Transactions on Image Processing, 12, 1338-1351. http://dx.doi.org/10.1109/TIP.2003.818640
- Lindenbaum, M., Fischer, M. and Bruckstein, A.M. (1994) On Gabor’s Contribution to Image-Enhancement. Pattern Recognition, 27, 1-8. http://dx.doi.org/10.1016/0031-3203(94)90013-2
- Ghael, S., Sayeed, A.M. and Baraniuk, R.G. (1997) Improved Wavelet Denoising via Empirical Wiener Filtering. Proceedings of SPIE, Wavelet Applications in Signal and Image Processing V, 3169, 389-399. http://dx.doi.org/10.1117/12.292799
- Donoho, D.L. (1995) Denoising by Soft-Thresholding. IEEE Transactions on Information Theory, 41, 613-627. http://dx.doi.org/10.1109/18.382009
- Buades, A., Coll, B. and Morel, J.M. (2005) A Review of Image Denoising Algorithms, with a New One. Multiscale Modeling and Simulation, 2, 490-530. http://dx.doi.org/10.1137/040616024
- Buades, A., Coll, B. and Morel, J.M. (2010) Image Denoising Methods. A New Nonlocal Principle. SIAM Review, 52, 113-147. http://dx.doi.org/10.1137/090773908
- Buades, A., Coll, B. and Morel, J.M. (2011) Non-Local Means Denoising. www.ipol.im/pub/algo/bcm_non_local_means-denoising/
- Mahmoudi, M. and Sapiro, G. (2005) Fast Image and Video Denoising via Non-Local Means of Similar Neighborhoods. IEEE Signal Processing Letters, 12, 839-842. http://dx.doi.org/10.1109/LSP.2005.859509
- Liu, Y.L., Wang, J. and Chen, X. (2008) A Robust and Fast Non-Local Means Algorithm for Image Denoising. Journal of Computer Science and Technology, 23, 270-279. http://dx.doi.org/10.1007/s11390-008-9129-8
- Tian, J., Yu, W.Y. and Xie, S.L. (2008) On the Kernel Function Selection of Nonlocal Filtering for Image Denoising. Proceedings of IEEE International Conference on Machine Learning and Cybernetics, Kunming.
- Tomasi, C. and Manduchi, R. (1998) Bilateral Filtering for Gray and Color Images. Proceedings of the International Conference on Computer Vision, Bombay, 839-846. http://dx.doi.org/10.1109/ICCV.1998.710815





















