Journal of Computer and Communications
Vol.2 No.6(2014), Article ID:45007,7 pages DOI:10.4236/jcc.2014.26003
Link Availability Prediction for Cognitive Radio Ad Hoc Networks
Ling Hou1, Kai-Hau Yeung1, Kin-Yeung Wong2
1City University of Hong Kong, Hong Kong, China
2The Open University of Hong Kong, Hong Kong, China
Email: linghou2-c@my.cityu.edu.hk, eeayeung@cityu.edu.hk, akywong@ouhk.edu.hk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 12 March 2014; revised 5 April 2014; accepted 13 April 2014
ABSTRACT
One critical issue for routing in cognitive radio ad hoc networks (CRAHNs) is how to select a reliable path for forwarding traffic. This is because mobility may cause radio links to break frequently. The reliability of a path depends on the availability of those links that constitutes the path. In this letter, we present a novel approach to predict the probability of the availability of the link between two cognitive radio nodes. The prediction is achieved by estimating the link activation and spectrum activation probabilities. Our prediction is verified by simulation and proved to be accurate. This study can provide reliability assurance on dynamic routing for cognitive radio ad hoc networks.
Keywords:Cognitive Radio, Ad Hoc Network, Spectrum Mobility, Link Availability

1. Introduction
Cognitive radio (CR) was proposed to make use of the existing wireless spectrum opportunistically without causing harmful interference or collisions to the primary users (PUs) [1] . Cognitive radio ad hoc networks (CRAHNs) are networks with mobile CR devices working without the support of any fixed infrastructure or central administration. Since the topology of a CRAHN can change rapidly and unpredictably, efficient routing is difficult to achieve in CRAHNs. Routing path in CRAHNs may break frequently due to dynamic network topology. If any single link of a path breaks, then this path needs to be either locally repaired by finding another link if possible or globally replaced with a new path by rerouting. Route repair or rerouting will induce more energy consumption, waste the scarce radio resources, and degrade end-to-end network performance such as throughput and delay [2] . Thus, an optimal path in CRAHNs should first be stable and reliable to avoid frequent rerouting operations. The stability of a path depends on the availability of all links constituting this path.
A large number of prediction models, such as [2] -[8] , are available for link availability prediction in the classical MANETs. In these networks, a link is considered to be available if the two nodes associated with this link are within the transmission range of each other. However, in CRAHNs, a link should also satisfy another requirement that the two nodes associated with this link have to have a common available spectrum channel to use. Thus, the prediction models for MANETs are not suitable for the link availability estimation in CRAHNs.
Two link availability prediction models for CRAHNs are proposed in [9] and [10] . In [9] , a time period Tp that the link between two CR nodes will stay available and its corresponding probability 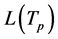 is predicted. Another time period
is predicted. Another time period 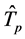 until either CR node of the link moves into the interference area of a PU and its corresponding probability
until either CR node of the link moves into the interference area of a PU and its corresponding probability  are also predicted. After that, the link availability is revealed by the combination of
are also predicted. After that, the link availability is revealed by the combination of 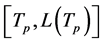 and
and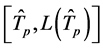 . In their work, each predicted time period is determined by velocities of CR nodes and the node distance. In [10] , the link availability is predicted in a fixed time interval. However, in reality, the link availability during flow transmitting time (traffic flow duration) is most important to routing. Therefore, unlike the previous work that predicting time period, we concentrate on predicting link availability throughout the traffic flow duration. The main contribution of this paper is a method to predict how the CR node mobility and PU activities affect the link stability throughout the traffic flow duration. By using the prediction method presented in this paper, a more stable routing path could be selected in order to avoid frequent link failure.
. In their work, each predicted time period is determined by velocities of CR nodes and the node distance. In [10] , the link availability is predicted in a fixed time interval. However, in reality, the link availability during flow transmitting time (traffic flow duration) is most important to routing. Therefore, unlike the previous work that predicting time period, we concentrate on predicting link availability throughout the traffic flow duration. The main contribution of this paper is a method to predict how the CR node mobility and PU activities affect the link stability throughout the traffic flow duration. By using the prediction method presented in this paper, a more stable routing path could be selected in order to avoid frequent link failure.
The rest of this paper is structured as follows. Section 2 describes the system model. A link-availability prediction scheme is presented in Section 3. The results given by this estimation are compared with simulation results in Section 4. Finally, Section 5 concludes this paper.
2. System Model
Since cognitive radio users (CUs) are considered to have lower priority and belong to secondary users of the spectrum allocated to PUs, CUs have to sense the spectrum to detect PU activities. Spectrum availability is only affected by PU activities in the scenario that the interference area of PUs is large enough to cover the CRAHN. In this letter, we study how the spectrum availability due to PU activities affects the network performance in CRAHNs.
We consider a cognitive radio ad hoc networks consisting of n cognitive radio users and m primary users. The PUs, who coexist in an overlapping region with the CUs, hold licenses for specific spectrum channels, and they are only allowed to utilize their assigned channel [2] . As CUs do not have any licensed spectrum, they can only opportunistically use the idle channels.
We denote the set of CR nodes as 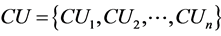 and the set of PUs as
and the set of PUs as 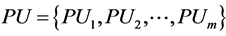 . We assume that PUi hold licenses for spectrum channel Chi. The channel Chi is busy when PUi arrives and uses it. Only when PUi is not present, the channel Chi can be used by CUs. Assume that the arrival rate of PUi to its assigned channel follows Poisson distribution with mean
. We assume that PUi hold licenses for spectrum channel Chi. The channel Chi is busy when PUi arrives and uses it. Only when PUi is not present, the channel Chi can be used by CUs. Assume that the arrival rate of PUi to its assigned channel follows Poisson distribution with mean . Note that PU activities and CU movements are independent of each other.
. Note that PU activities and CU movements are independent of each other.
In this letter, we consider that CUs move in random walk mobility model. Based on this model, the movement of a CU consists of a sequence of random length intervals called mobility epochs. During a mobility epoch, a node moves in a constant direction at a constant speed. The speed and direction of each node varies randomly from epoch to epoch. Mobility epoch durations are exponentially distributed. Speed, direction and epoch length are uncorrelated. Besides, the mobility of the CUs are independent with each other.
The mobility epoch is illustrated in Figure 1. The speed 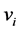 and direction
and direction  of node CUi during each epoch are uniformly distributed over the ranges of
of node CUi during each epoch are uniformly distributed over the ranges of 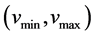 and
and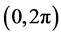 , respectively. The mobility epoch duration of node CUi is exponentially distributed with mean
, respectively. The mobility epoch duration of node CUi is exponentially distributed with mean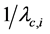 . When the epoch starts, the initial position of CUi is at
. When the epoch starts, the initial position of CUi is at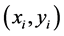 , the initial position of CUj is at
, the initial position of CUj is at  and the initial distance between CUi and CUj is d0. After time period t during the mobility epoch, the position of CUi can be expressed as
and the initial distance between CUi and CUj is d0. After time period t during the mobility epoch, the position of CUi can be expressed as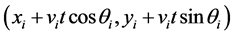 . Then, the distance dt after time period t can be expressed as
. Then, the distance dt after time period t can be expressed as
 (1)
(1)
where, 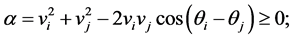
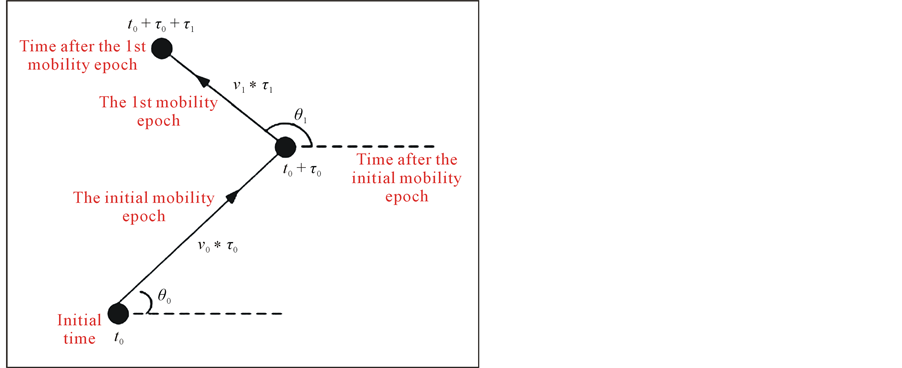
Figure 1. Radom mobility epoch model.
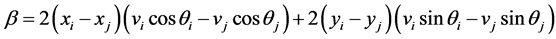 .
.
3. Link Availability Estimation
Let t0 denote the initial time instant and Tf denote the traffic flow duration time. And the link from CUi to CUj on channel Chk is denoted by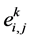 . In this section, we propose a link availability estimation method to predict the link availability from t0 to
. In this section, we propose a link availability estimation method to predict the link availability from t0 to .
.
Before explaining the method for estimating the link availability grade, the definition of link availability is provided in what follows:
Definition 1. A link between two nodes CUi and CUj with transmission rangeR is defined to be link connected at time instant t, when the distance between both nodes is such that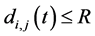 . Figure 2 shows a simple example in which the link between nodes CUi and CUj is connected initially but then become deactivated after a mobility epoch. The probability of link connected from t0 to
. Figure 2 shows a simple example in which the link between nodes CUi and CUj is connected initially but then become deactivated after a mobility epoch. The probability of link connected from t0 to 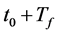 is defined as link connection probability and denoted by
is defined as link connection probability and denoted by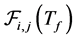 .
.
Definition 2. A link between two nodes CUi and CUj is defined to be spectrum available on channel Chk at time instantt , when the channel Chk is available for the link to use at time instant t. That is, Chk is not utilized by its licensed user at time t. We denote the probability of spectrum availability from t0 to 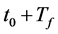 by
by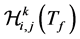 .
.
Definition 3. A link between two nodes CUi and CUj is defined to be available on channel Chk at time instantt if the link is both link connected and spectrum available.
Definition 4. A link between two nodes CUi and CUj is defined to be available on channel Chk during time t0 to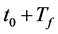 , if the link is continuously available from t0 to
, if the link is continuously available from t0 to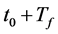 . The probability of link continuously available from t0 to
. The probability of link continuously available from t0 to 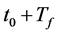 is defined as link availability and denoted by
is defined as link availability and denoted by .
.
Link availability is dependent on link connection probability and spectrum availability probability. Link connection probability is affected by CUs’ movement. We neglect the spectrum contention among CUs. We assume that spectrum availability is only dependent on PU activity. And as mentioned earlier, CU movement and PU activity are independent of each other. Thus, for a link , its link availability
, its link availability 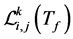 is given by
is given by
 (2)
(2)
It is easy to calculate , which is equal to the probability that PUk will not arrive to use channel Chk from t0 to
, which is equal to the probability that PUk will not arrive to use channel Chk from t0 to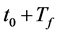 . Given the Poisson arrival process with parameter
. Given the Poisson arrival process with parameter , then the probability of zero arrivals to the licensed channel Chk is given by
, then the probability of zero arrivals to the licensed channel Chk is given by
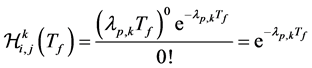 . (3)
. (3)
However, it is difficult to give an accurate calculation for 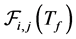 because of the difficulties in estimating
because of the difficulties in estimating
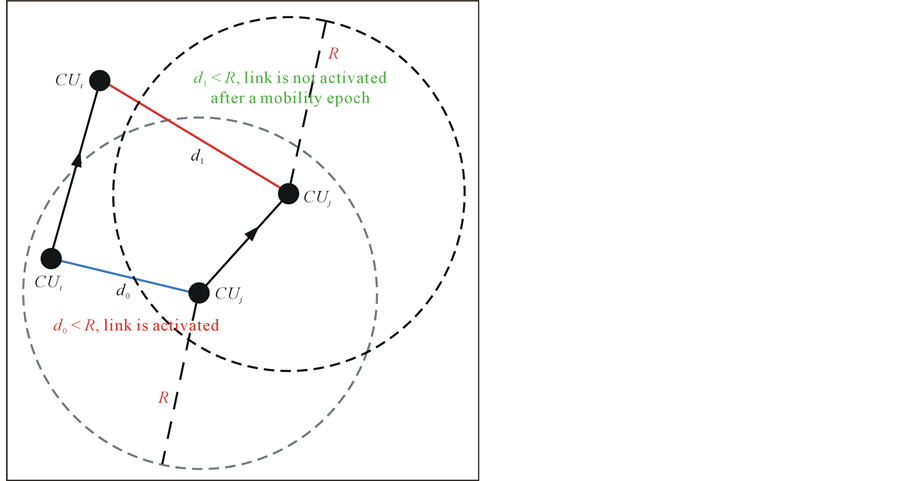
Figure 2. Link mobility and activation example.
the movement of CR users. In the following, we discuss an estimation method for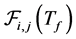 .
.
Since the mobility epoch lengths of CUs follow exponential distribution, the process for a node to change its velocity is Poisson with a mean rate equal to the reciprocal of the mean epoch [5] . According to the assumption that the movement of each CR user is independent, then the probability for X changes in velocities (or consist of X + 1 mobility epochs) to happen to a link 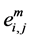 is denoted as
is denoted as 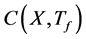 and given by
and given by
 (4)
(4)
where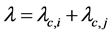 .
.
A mobility epoch to a link is a time period during which both nodes associated with this link will not change their velocities. Let  denote the probability that link
denote the probability that link 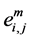 can be still continuously available with X changes in velocities happening within
can be still continuously available with X changes in velocities happening within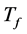 . Let
. Let  denote the time duration of the kth mobility epoch, where
denote the time duration of the kth mobility epoch, where and
and . Then, the probability that link
. Then, the probability that link  will be continuously activation within
will be continuously activation within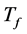 is expressed as
is expressed as
 . (5)
. (5)
The link connection state of a link 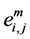 at the end of a mobility epoch can be regarded as a random variable, whose state space is
at the end of a mobility epoch can be regarded as a random variable, whose state space is , where 0 corresponds to link activation and 1 corresponds to not activation. Let
, where 0 corresponds to link activation and 1 corresponds to not activation. Let  denote the link activation probability during the kth mobility epoch given that the link
denote the link activation probability during the kth mobility epoch given that the link 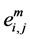 is connected during the last mobility epoch. Then, the state transition matrix of the kth mobility epoch is defined as
is connected during the last mobility epoch. Then, the state transition matrix of the kth mobility epoch is defined as
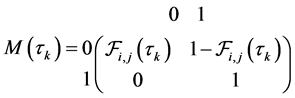 .
.
For a initially activated link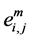 , we have the initial vector
, we have the initial vector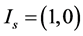 . The final vector can be derived as
. The final vector can be derived as . Then,
. Then,  is expressed as
is expressed as
 . (6)
. (6)
Lemma 1. If a link is connected at the initial and at the end of a mobility epoch, then the link is continuously connected during this mobility epoch.
Proof. Let  denote link distance after an epoch of
denote link distance after an epoch of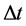 . Given the initial distance of a link is d0 and both nodes associated with this link will not change their velocities during
. Given the initial distance of a link is d0 and both nodes associated with this link will not change their velocities during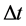 , according to (1),
, according to (1), 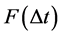 can be expressed as
can be expressed as
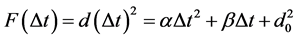 .
.
where 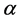 and
and  are constant, and
are constant, and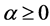 .
.
Then, . Accordingly, the function
. Accordingly, the function 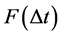 is convex downward. Let d1 denote the link distance at the end of the mobility epoch. And thus,
is convex downward. Let d1 denote the link distance at the end of the mobility epoch. And thus, 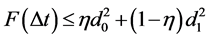 , where
, where .
.
If a link is available at the initial and at the end of a mobility epoch, then d0 and d1 both satisfy the link activation requirement (d0 ≤ R and d1 ≤ R). Therefore, 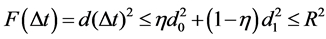 , which represents that the link distance satisfies the link activation requirement all the time during the mobility epoch.
, which represents that the link distance satisfies the link activation requirement all the time during the mobility epoch. 
Let  denote the initial time of the kth mobility epoch. Also let
denote the initial time of the kth mobility epoch. Also let  denote the probability that link
denote the probability that link 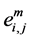 is activated at
is activated at  given it is activated at
given it is activated at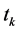 . According to Lemma 1, then the problem of calculating continuous link activation probability
. According to Lemma 1, then the problem of calculating continuous link activation probability 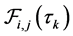 can be obtained by calculating the non-continuous link activation probability
can be obtained by calculating the non-continuous link activation probability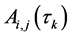 .
.
It is easy to calculate 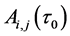 because initial distance between nodes
because initial distance between nodes  and
and  and the velocities of them are known. Based on the known information, the value of
and the velocities of them are known. Based on the known information, the value of  and
and 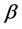 in Equation (*6) can be determined.
in Equation (*6) can be determined.
Assuming that , then
, then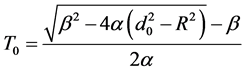 . If
. If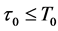 , then
, then ; if otherwise,
; if otherwise,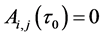 .
.
However, for the mobility epochs after the initial epoch, the velocities and link distance are not known. Therefore, according to the conclusion from [3] , then
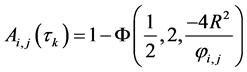
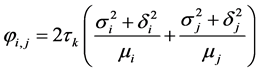
4. Numerical Result
In this section, the correctness of the proposed approach is verified via computer simulations. The simulated environment is a two dimensional space (500, 500), which represents an area of size 500 meters by 500 meters. CR nodes are randomly moving in the 2-D space according to the random-walk based mobility model, where a node moves with a direction uniformly and a speed uniformly from 0 to  with exponentially distributed epochs. The maximum transmission range of each node is 300 meters, and the transmission rate is 2 Mb/s. Then we statistically calculated the probability that the link was continuously available for t seconds based on all the experimental results. Each curve shown in Figure 3 is a result of 15,000 independent experiments.
with exponentially distributed epochs. The maximum transmission range of each node is 300 meters, and the transmission rate is 2 Mb/s. Then we statistically calculated the probability that the link was continuously available for t seconds based on all the experimental results. Each curve shown in Figure 3 is a result of 15,000 independent experiments.
In Figure 3, each plot is composed of two curves: simulation results and estimation results. As shown in the figure, the estimation results are very close with the simulation results, implying that our research can be applied to predict link availability in actual mobile environments. We can also observe that in a high dynamic environment (high speed of CR nodes or high arrival rate of primary users), link availability drops quickly as t increases. For example, when the maximum velocity is 5 m/s, as time goes by, link availability drops more quickly than the situation when the maximum velocity is 2 m/s. Similarly, as shown in Figure 3, when the arrival rate of primary users is 0.02, as time goes by, link availability drops more quickly than the situation when the arrival rate is 0.01. Therefore, the ability of predicting link availability for a short period of time is very important for CRAHNs, especially in a highly dynamic network environment.
5. Conclusion and Future Work
In this letter, we develop a mathematical model for link availability estimation in cognitive radio ad hoc networks with a random walk mobility model. Our approach is to predict the probability that the link will be
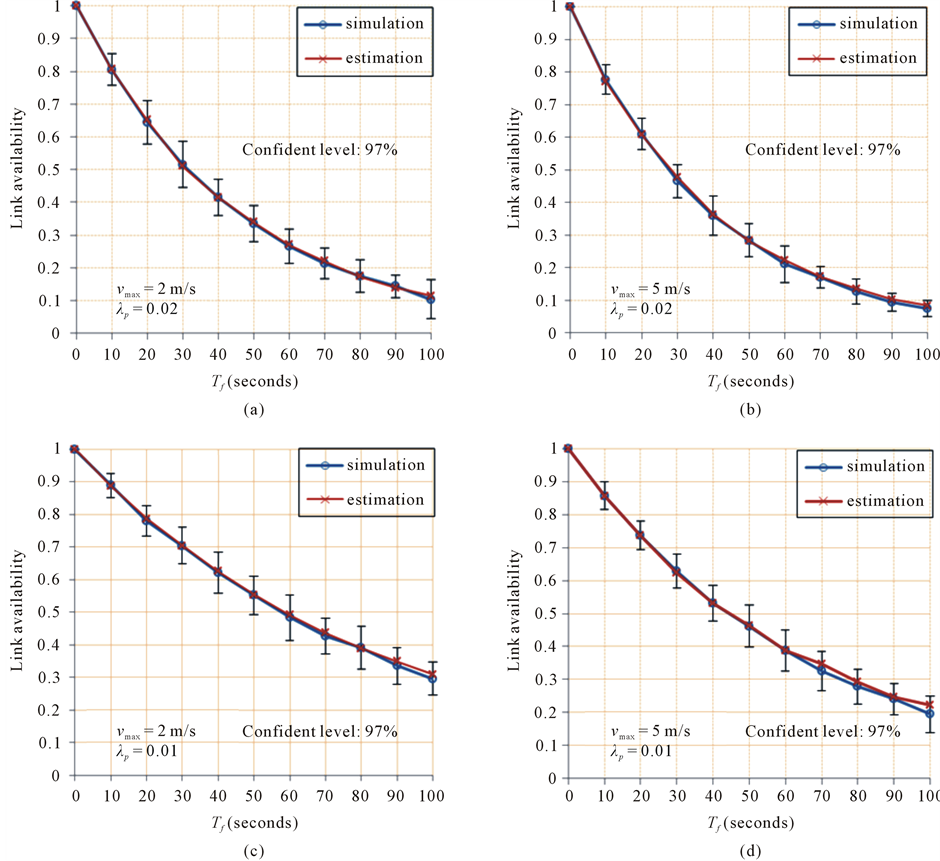
Figure 3. Simulation and predicted results.
continuously available during traffic flow duration. Simulation results reveal that our proposed link availability estimation approach can accurately predict link availability. Our work can provide reliability assurance on dynamic routing for cognitive radio ad hoc networks. The transmission range is assumed to be the same in all directions in this paper. To make it more practical, our future work is to develop an irregular transmission model to predict more comprehensive link availability.
Funding
This work was supported by City University Strategic Research Grant No. 7002734.
References
- Akyildiz, I.F., Lee, W.Y. and Chowdhury, K. (2009) CRAHNs: Cognitive Radio Ad Hoc Networks. Ad Hoc Networks Journal (Elsevier), 7, 810-836. http://dx.doi.org/10.1016/j.adhoc.2009.01.001
- Jiang, S.M., He, D.J. and Rao, J.Q. (2001) A Prediction-Based Link Availability Estimation for Mobile Ad-Hoc Networks. Proceedings IEEE International Conference on Computer Communications (INFOCOM’01), 3, 1745-1752.
- McDonald, A.B. and Znabi, T.F. (1999) A Mobility-Based Framework for Adaptive Clustering in Wireless Ad Hoc Networks. IEEE Journal on Selected Areas in Communications, 17, 1466-1487. http://dx.doi.org/10.1109/49.780353
- Bai, Y. and Gong, L. (2010) Link Availability Prediction with Radio Irregularity Coverage for Mobile Multi-Hop Networks. IEEE Communications Letters, 14, 518-520. http://dx.doi.org/10.1109/LCOMM.2010.06.100238
- Jiang, S. (2004) An Enhanced Prediction-Based Link Availability Estimation for MANETs. IEEE Transactions on Communications, 52, 183-186. http://dx.doi.org/10.1109/TCOMM.2003.822739
- Egeland, G. and Engelstad, P.E. (2009) The Availability and Reliability of Wireless Multi-Hop Networks with Stochastic Link Failures. IEEE Journal on Selected Areas in Communications, 27, 1132-1146. http://dx.doi.org/10.1109/JSAC.2009.090910
- Han, Q., Bai, Y., Gong, L. and Wu, W. (2010) Link Availability Prediction-Based Reliable Routing for Mobile Ad Hoc Networks. IET Communications, 5, 2291-2300. http://dx.doi.org/10.1049/iet-com.2010.0946
- Song, Q.Y., Ning, Z.L., Wang, S.Q. and Jamalipour, A. (2012) Link Stability Estimation Based on Link Connectivity Changes in Mobile Ad-Hoc Networks. Journal of Network and Computer Applications, 35, 2051-2058. http://dx.doi.org/10.1016/j.jnca.2012.08.004
- Guan, Q., Yu, F.R., Jiang, S. and Wei, G. (2010) Prediction-Based Topology Control and Routing in Cognitive Radio Mobile Ad Hoc Networks. IEEE Transactions on Vehicular Technology, 59, 4443-4452. http://dx.doi.org/10.1109/TVT.2010.2069105
- Caleffi, M., Akyildiz, I.F. and Paura, L. (2012) OPERA: Optimal Routing Metric for Cognitive Radio Ad Hoc Networks. IEEE Transactions on Wireless Communications, 11, 2884-2894.

