Journal of Computer and Communications
Vol.1 No.4(2013), Article ID:38196,9 pages DOI:10.4236/jcc.2013.14003
Analytical Evaluation of Space-Time M-QAM Signaling and Time-Delay Estimation in Multipath Terrestrial Communications
![]()
School of Electronic, Electrical and Computer Engineering, University of Birmingham, Birmingham, UK.
Email: rahimian@ieee.org
Copyright © 2013 Ardavan Rahimian. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 6th, 2013; revised October 4th, 2013; accepted October 11th, 2013
Keywords: MIMO; STBC; TDE; Terrestrial; Turbo Code
ABSTRACT
This paper presents novel information-theoretic PHY layer performance improvement for combating the system fading effects in wireless terrestrial communication applications. Robust space-time system strategies in cooperation with the high performance unpunctured serially concatenated codes have been jointly employed. The wireless terrestrial system also uses M-ary quadrature amplitude modulation (QAM) signaling to develop a well-established system modeling for multiple-input single-output (MISO) and multiple-input multiple-output (MIMO) analysis. This research also undertakes the analytical evaluation of time delay estimation in the presence of additive white Gaussian noise (AWGN) in multipath areas. The objective of this investigation is to develop mathematically-oriented estimations intended for a suitable employment in terrestrial communications. This model considers the problem of overlapping the terrestrial signals arrival-times estimation from a noisy received waveform in order to develop a system model for terrestrial TDE.
1. Introduction
The increasing demands for improving physical (PHY) layer system performance of wireless systems constitute a thriving global industry. Hence, in order to fulfill PHY layer QoS requirements in modern terrestrial systems, the appropriate combination of wireless technologies for constituting an engineering trade-off in terms of the overall system’s bit error rate (BER), and the estimated complexities should be considered. After the introduction of the Alamouti dual-antenna space-time codes [1] which appeal in terms of its performance and complexity, the proposed scheme motivated Tarokh to generalize the Alamouti’s scheme to an arbitrary number of antennas [2, 3], leading to the concept of the orthogonal space-time block codes (STBCs) [4]. STBCs have then evolved at an exceptional rate and reached a state of maturity in theory after their breakthrough discovery; they quickly found their way into the practical applications and standards for enabling outstanding reliable technologies such as: LTE, WLAN, WMN, WiMAX, and RFID [5-8]. In order to satisfy the reliability requirements in the systems, highperformance forward error correction (FEC) codes are required in addition to transmit/receive spatial diversity. Turbo codes [9] brought about a wealth of theoretical knowledge and practical solutions for achieving coding gains with feasible decoding complexities. They have been adopted in various wireless standards due to nearcapacity performance, including the ITU-proposed 3G standards [10], ETSI-DVB system [11], UMTS [12], and LTE [13]. In this research, performance analysis of the dual antenna space-time codes based on the Alamouti along with the Tarokh’s orthogonal STBCs has been evaluated in cooperation with the high-performance turbo coding scheme. The performance evaluations have been carried out over multiple-input single-output (MISO) and multiple-input multiple-output (MIMO) systems. These systems are operating in the statistical wireless terrestrial communications propagation environment. Hence, terrestrial reliable wireless system deployment is necessary in order to provide highly accurate and efficient services, and is also of crucial importance for modern wireless technologies. The enormous growth in terrestrial communications and with the increasing demand for the highperformance services raise the need for systems analysis and planning for the intended environments to evaluate performance and its operation estimation. The problem of wireless time-delay estimation (TDE) is of considerable research interest in the wireless communications, which is related to the multipath in specified environments. Multipath causes a single transmitted signal originnating from a source to arrive at a receiver via two or more different paths along with any combination of several distinct unequal length paths. These extra paths at a receiver can be synchronized with the mean scaling of the most dominant path and all the others are treated as the noise; then possible equalization strategies can be employed to improve the receiver system performance [14,15]. It is assumed that the transmitted radio signal and the number of paths in the multipath environment are known. The received radio signal is not just the transmitted one, but several delayed and amplitude-weighted versions of the transmitted signal [16].
2. Terrestrial Communication TDE Theory
The problem of multipath time-delay estimation (MTDE) in this research has been characterized using (1) as:
 (1)
(1)
where s(t) is the transmitted radio signal (system pulse); ak is the amplitude (attenuation value) for path k; tk is the time-delay for path k; M is the number of different paths; and 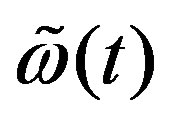 is the white Gaussian noise (AWGN) in the multipath environment. The correlation receiver is used to obtain the time-delay estimates. If the TDEs are estimated in a multipath environment where paths are spaced closer than a correlation time of a transmitted radio signal, the receiver cannot separate the closely spaced delays. When the terrestrial radio structure is utilized for the estimation, fading effects can be alleviated and significant wireless system performance improvement can be achieved [17].
is the white Gaussian noise (AWGN) in the multipath environment. The correlation receiver is used to obtain the time-delay estimates. If the TDEs are estimated in a multipath environment where paths are spaced closer than a correlation time of a transmitted radio signal, the receiver cannot separate the closely spaced delays. When the terrestrial radio structure is utilized for the estimation, fading effects can be alleviated and significant wireless system performance improvement can be achieved [17].
3. Terrestrial Communication System Model
Figure 1 shows block diagram of the STBC coded wireless MIMO system of interest, employing QAM as the modulation scheme, and turbo codes as a state-of-the-art FEC. The information bit sequence is first fed into a turbo encoder and then modulated in a multilevel QAM modulator where the coded system bit stream is first blocked into a symbol of 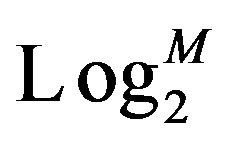 data bit i.e. four data bits in this case; it should be considered as an appropriate operating point in system power versus spectral efficiency trade-off, since 16-QAM have moderate theoreticcal bandwidth efficiency in M-QAM signaling scheme [4 (bit/sec)/Hz] that is 1 (bit/sec)/Hz for 2-QAM (i.e. BPSK), and 8 (bit/sec)/Hz for 256-QAM, while yields moderate
data bit i.e. four data bits in this case; it should be considered as an appropriate operating point in system power versus spectral efficiency trade-off, since 16-QAM have moderate theoreticcal bandwidth efficiency in M-QAM signaling scheme [4 (bit/sec)/Hz] that is 1 (bit/sec)/Hz for 2-QAM (i.e. BPSK), and 8 (bit/sec)/Hz for 256-QAM, while yields moderate
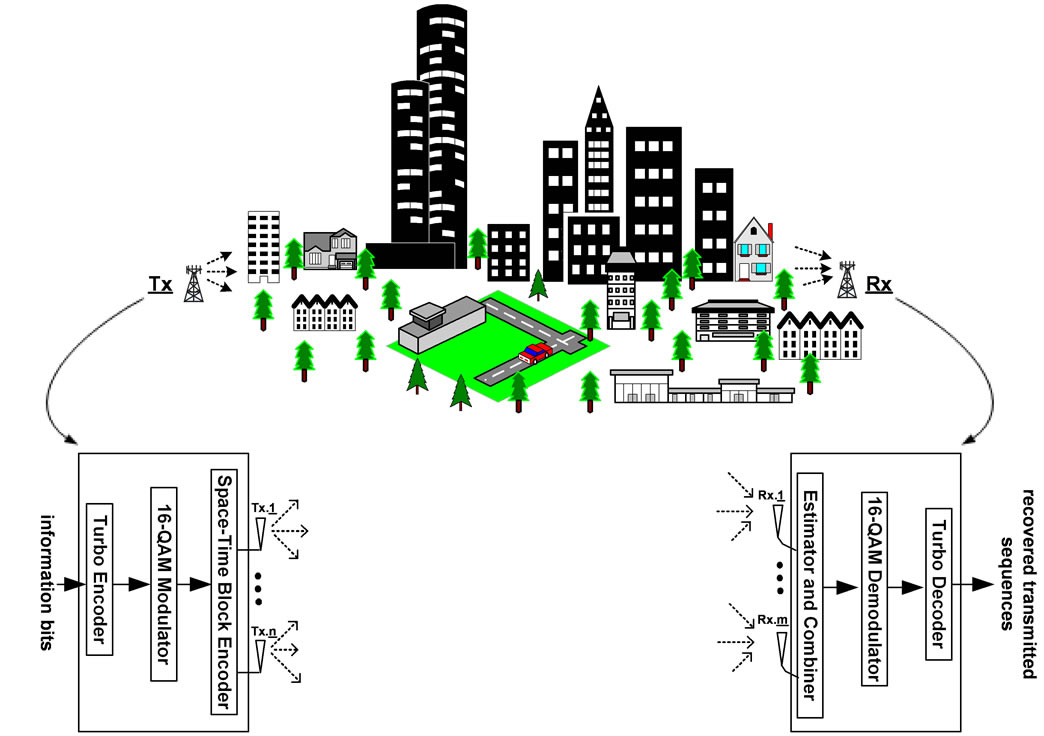
Figure 1. Terrestrial communications environment block diagram.
power efficiency compared with other M-QAM schemes according to the theoretical BER bounds for uncoded M-QAM over the additive white Gaussian noise (AWGN) channel, for resulting in the BER of 10−6, and 16-QAM operating SNR is 14.5 dB, while that is 10.5 dB and 23.5 dB for M = 2 and M = 256 schemes respectively. Hence, it has been introduced in various standards such as DVBTerrestrial, HSDPA protocol, and IEEE 802.11a PHY for modulating OFDM subcarriers. The modulated symbols are mapped using space-time block encoder which has advantages of both the spatial diversity provided by multiple antennas, and the temporal diversity available with time-varying fading [18], without channel state information (CSI) [19]. At the receiver, the combiner combines received signals which are then sent to the maximum likelihood (ML) detector. The detected symbols are then demodulated by the multilevel QAM demodulator and are sent to the iterative turbo decoder for recovering the transmitted information bits in the terrestrial radio system transmissions.
4. Terrestrial Communication FEC Coding
Turbo codes have attracted a great interest after their advent [9] since they were the first class of error correcting codes that could perform within a fraction of a decibel to capacity limit [20]. The classic turbo coding is a channel coding technique based on the idea of producing long and random code which employs an iterative decoding algorithm to result in BER performance near capacity limit. The encoder of classic turbo codes is constructed by parallel concatenating two recursive systematic convolutional (RSC) codes through an interleaver. They have been termed as parallel concatenated codes (PCCs) as well. The decoder consists of an interleaver linked soft-input soft-output constituent decoders for corresponding RSC codes. Owing to the presence of the system’s interleaver, optimum ML decoding algorithms for turbo codes are very complex. However, iterative decoding of codes in which soft-information is exchanged between constituent decoders is quite feasible and leads to near capacity performance. This information could be regarded as a type of diversity that can refine the constituent decoder’s outputs in iterations and in the TDE analysis [21]. An enhanced iterative turbo decoder structure using a modified version of the conventional maximum a posteriori (MAP) algorithm [22] was invoked to decode the introduced PCCs. For preserving the performance of the original MAP decoding with the relatively lower complexities, practical reduced complexity decoding approaches were then proposed. These system decoding algorithms introduced include Max Log-MAP [23], Log-MAP [24], and Erfanian scheme [25]. After achieving the system error correction characteristics close to the Shannon limit at a BER of 10−5 (at Eb/N0 = 0.7 dB with code rate of 1/2) based on PCCs, a vast body of efforts are dedicated to develop the codes.
Unfortunately, in many turbo coded wireless systems, it is reported that for BERs lower than 10−5, the increase in transmit power just marginally reduces the BER values. As a strong technique to sharpen the system BER curve in error-floor region, turbo codes based on serial concatenation of convolutional codes were introduced which reported excellent results from this scheme in moderate to high SNRs [26]. Serial turbo codes which are referred to as serially concatenated codes (SCCs) behave significantly better and do not exhibit the typical error-floor behavior of the PCCs. In cases where relatively smaller interleaver size is employed, PCC’s error-floor starts at a much higher BER value of 10−3, while the SCCs have shown to exhibit sharp curve for BERs lower than 10−3 [27]. The SCC’s encoder consists of the cascade of an outer convolutional code, an interleaver, and also an inner convolutional code whose system input words are the permuted version of outer codewords. The turbo system decoding algorithm in both the SCCs and PCCs are the same. However, it should be noted that the primary difference is that while in the structure of PCCs both the constituent decoders make use of direct output from the demodulator, in SCC’s decoder only the inner decoder makes use of this information directly, and the outer one receives the relative extrinsic system information from the deinterleaved codewords of inner decoder’s outputs. In the context of designing SCCs, the following parameters have key roles in the turbo coded BER performance: constituent code; interleaver design; and decoding algorithm [28]. A practical performance parameter combination in the design of constituent codes and iterative decoder is utilized for yielding promising tradeoff in terms of BER and complexity. SCCs have been also employed based on quadratic interleavers proposed in [29] which have not only shown to have better BER performance in both waterfall and error-floor regions compared with the classic interleavers [30], but also have straightforward system implementation [31]. In [30], extra coding gain of 2.5 - 3 dB for yielding the BER of 10−5 has been reported, when quadratic interleaver is used in SCCs for both the SISO and MISO systems over Rice multipath fading channel; compared with the wireless communication system using matrix-based block interleavers with large and comparable system depth and span.
5. Terrestrial Space-Time Coding
For suppressing multipath effects, diversity techniques like time, frequency, and spatial diversity could be employed. Recent multiple antenna systems based on the space-time codes in which devices are equipped with the multi-transmit and receive antennas, have received considerable attention for research, not only from the theoretical aspects, but also in development and implementation for wireless systems. They are expected to play a major role in futuristic wireless communication systems due to their high diversity order and low decoding complexities, which lead to significantly improve reliability and dramatically increase capacity of wireless systems links [32-35]. Space-time encoding is performed according to the number of the transmit antennas, and the code rate. For rate one of the twin-antenna space-time codes, denoting the signal transmitted from the first and second antennas by s1 and s2, the encoding and transmission sequences are shown in Table 1. The encoding and also transmission sequences for the half-rate three transmit antennas are presented in Table 2. The transmission model is based on transmitting signals 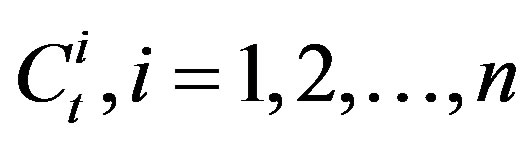 simultaneously from the n transmit antennas at each time slot of t, under the assumption that the wireless channel is quasi-static (so that the path gains are considered to be constant over a frame of length l and vary from one frame to the other one), and flat fading [3]. Defining the path gain from transmit antenna i to the receive antenna j by αi,j and also denoting the noise samples by
simultaneously from the n transmit antennas at each time slot of t, under the assumption that the wireless channel is quasi-static (so that the path gains are considered to be constant over a frame of length l and vary from one frame to the other one), and flat fading [3]. Defining the path gain from transmit antenna i to the receive antenna j by αi,j and also denoting the noise samples by 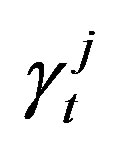 (i.e. independent samples of a zero mean complex Gaussian random variable with variance n/(2SNR) per complex system dimension), the received radio signal at the system antenna j at the time t is given as Equation (2) [3]:
(i.e. independent samples of a zero mean complex Gaussian random variable with variance n/(2SNR) per complex system dimension), the received radio signal at the system antenna j at the time t is given as Equation (2) [3]:

Table 1. Terrestrial Encoding and Transmission Sequence for Two Transmit Antennas; Alamouti Scheme; Code Rate: 1.
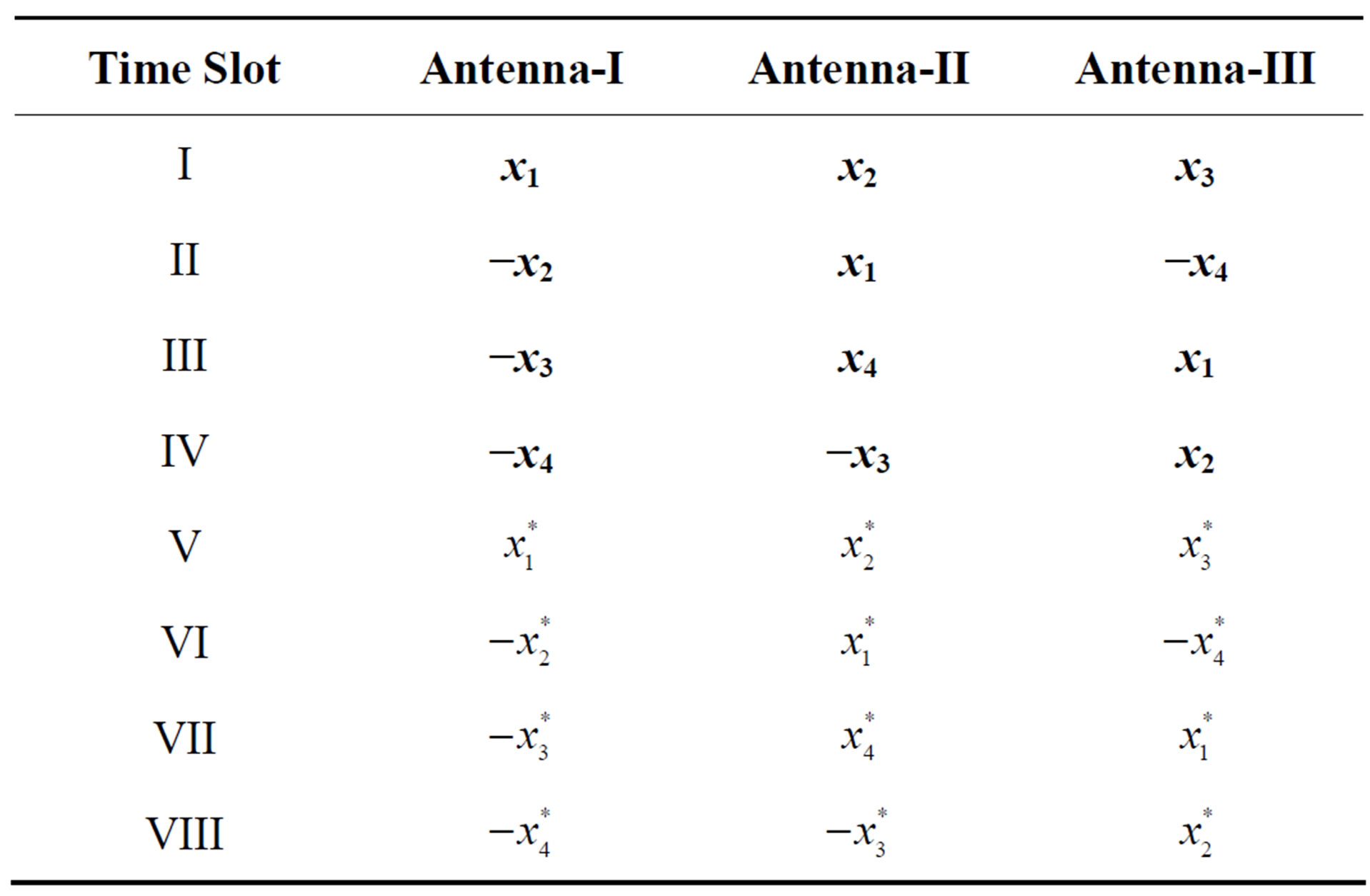
Table 2. Terrestrial Encoding and Transmission Sequence for Three Transmit Antennas; Tarokh Scheme; Code Rate: 1/2.
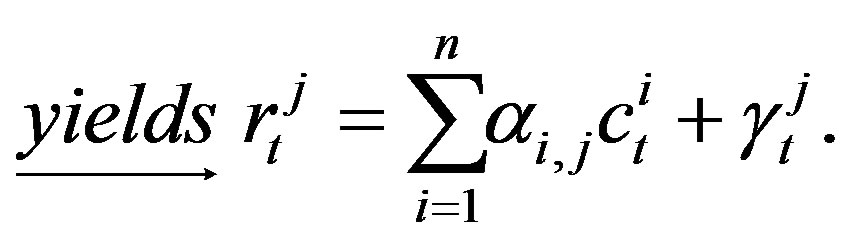 (2)
(2)
The system’s average energy of each transmitter antenna’s symbols is normalized to one so that the average power of each receive antenna’s radio signal is n. The receiver computes the decision metric given by the (3) over all the codewords, under the assumption that prefect channel impulse response (CSI) is available, and decides in favor of codeword that minimizes the sum [3]. The received signal is processed first in the channel estimator and combiner, and the combined received radio signals are then sent out to the system ML detector. In order for the wireless system to detect symbols of the two transmit antennas; denoted by s1 and s2; the decision metrics [36] have been potentially employed. For detecting symbols of half-rate three transmit antennas; denoted by s1, s2, s3; the decoder minimizes the decision metrics, as in [36].
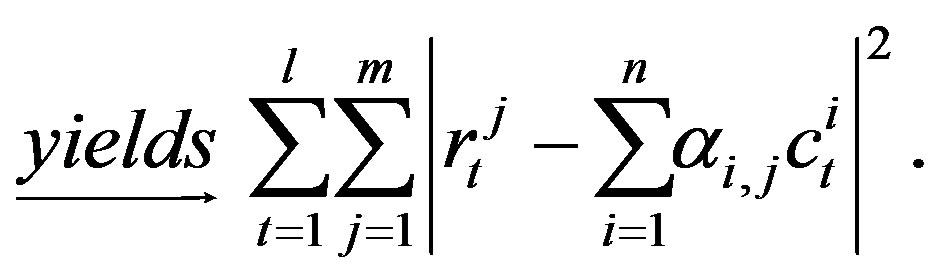 (3)
(3)
6. Terrestrial MIMO Channel Modeling
From system level aspect MIMO channel is represented by a N × M matrix H; the received terrestrial radio signal 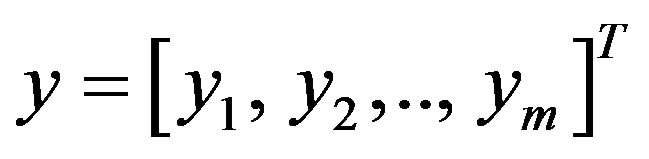 can also be expressed as [37]:
can also be expressed as [37]:
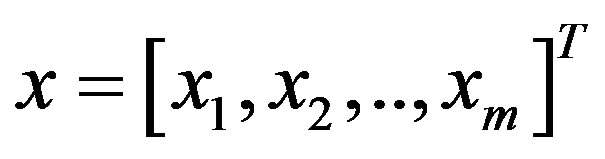
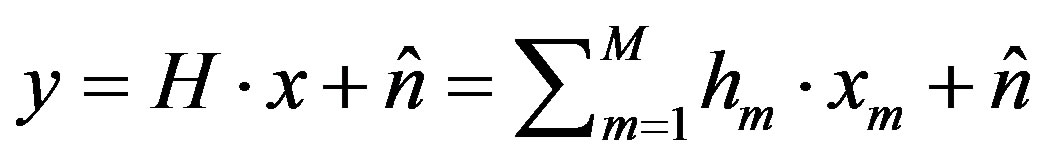 is the transmitted vector,
is the transmitted vector, 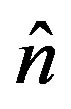 is the N × 1 additive white Gaussian noise (AWGN). If the number of receive antennas is reduced to one (i.e. for MISO systems), the MISO’s CIS can then be considered as N SISO channels expressed as 1 × N vector. It is assumed that nt transmit and nr receive antennas are placed in uniform linear arrays of normalized lengths Lt and Lr respectively. The normalized separation between transmit antennas Δt and the normalized separation between the receive antennas Δr are given:
is the N × 1 additive white Gaussian noise (AWGN). If the number of receive antennas is reduced to one (i.e. for MISO systems), the MISO’s CIS can then be considered as N SISO channels expressed as 1 × N vector. It is assumed that nt transmit and nr receive antennas are placed in uniform linear arrays of normalized lengths Lt and Lr respectively. The normalized separation between transmit antennas Δt and the normalized separation between the receive antennas Δr are given: 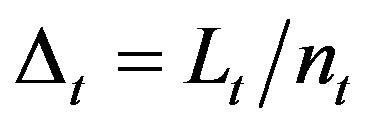 and
and 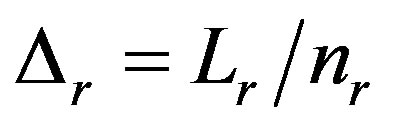 respectively; where the system normalization is by the wavelength of the passband transmitted radio signal λc [37]. It is then supposed there is an arbitrary number of physical paths between the transmitter and receiver, and the attenuation of path
respectively; where the system normalization is by the wavelength of the passband transmitted radio signal λc [37]. It is then supposed there is an arbitrary number of physical paths between the transmitter and receiver, and the attenuation of path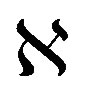 , and its angles with the transmit and receive system array are denoted as:
, and its angles with the transmit and receive system array are denoted as: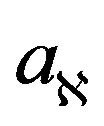 ,
, 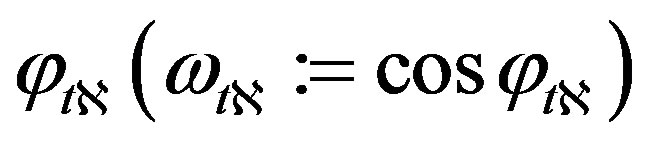 , and
, and 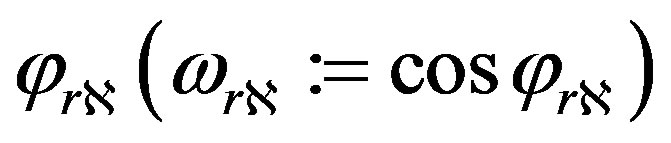 . Channel matrix H is given as the following equations; where
. Channel matrix H is given as the following equations; where 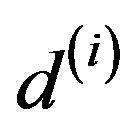 denotes the distance between the system transmit antenna 1 and the receive antenna 1, along the path
denotes the distance between the system transmit antenna 1 and the receive antenna 1, along the path 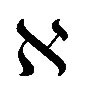 in radio transmission [37].
in radio transmission [37].
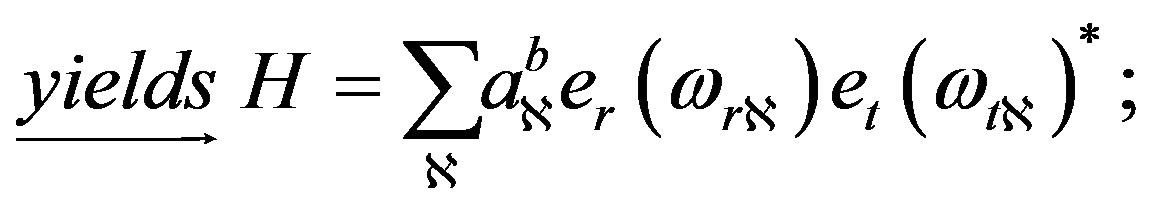 (4)
(4)
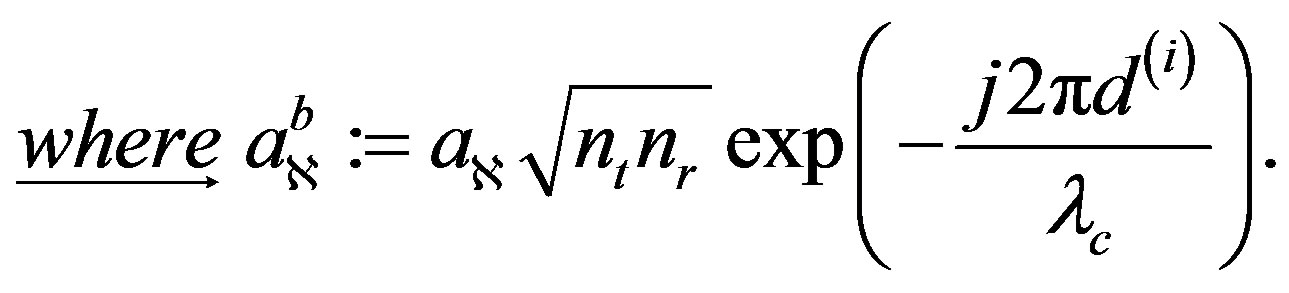 (5)
(5)
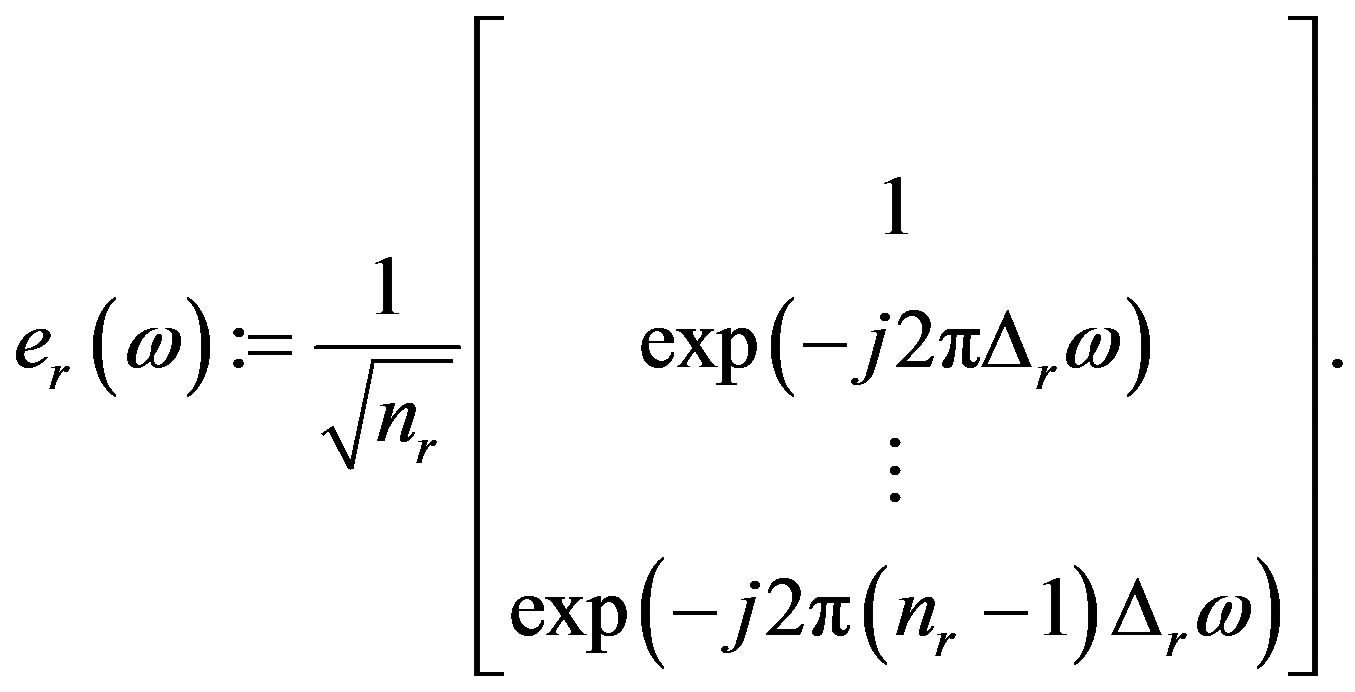 (6)
(6)
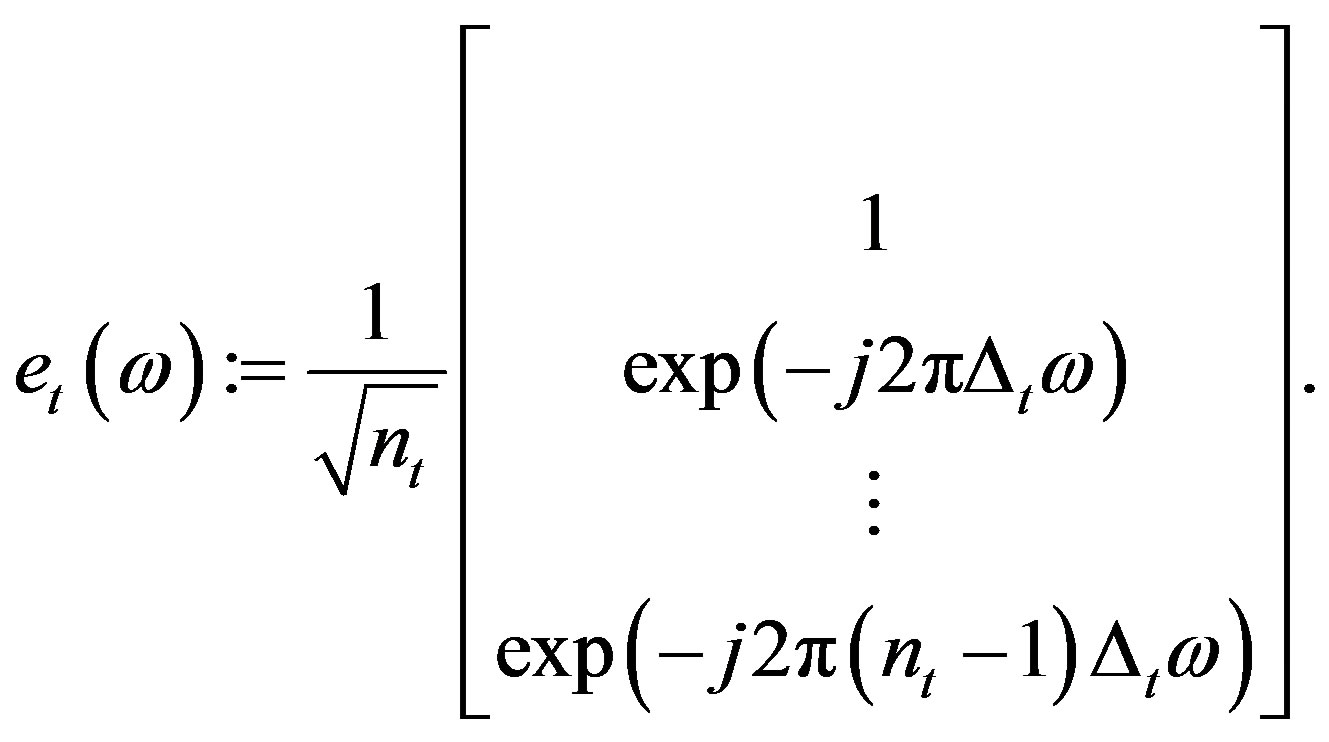 (7)
(7)
The column vectors: 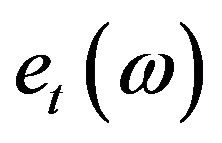 and
and  are the transmitted and received unit spatial signatures along direction ω respectively. There are two primary applications for the channel models: location-specific models which provide very accurate models robust with respect to small errors, for optimizing a system in a certain geographical region (for the planning and deployment). Simplified channel models that describe the CIR statistics in a parametric form; in which the number of parameters is small, and is independent of the specific locations. The models which are reflecting the important properties of propagation channels are used for the design, testing, and type approval of wireless systems [38]. For comparing different MIMO systems and their relevant PHY layer performance enhancement techniques in a manner that is unified and agreed on by many system parties, various organizations introduce the reference channel models with reproducible conditions [38]. Among these modeling methods utilized in site-specific and generic channel model applications (i.e. stored CIR, deterministic channel models, and also stochastic system channel models), the latter one is then selected which describes the predicted probability density function (PDF) of the CIR over a large area. In this research, stochastic modeling of the received radio signal’s amplitude is described by Rayleigh distribution which is used model for predicting PDF of the CIR; in the urban areas with blocked line-of-sight (LoS). Meanwhile, the COST207 models proposed bivariate Gaussian Doppler spectrum for modeling long echoes in urban propagation environments (models in the urban areas) [38]; given by:
are the transmitted and received unit spatial signatures along direction ω respectively. There are two primary applications for the channel models: location-specific models which provide very accurate models robust with respect to small errors, for optimizing a system in a certain geographical region (for the planning and deployment). Simplified channel models that describe the CIR statistics in a parametric form; in which the number of parameters is small, and is independent of the specific locations. The models which are reflecting the important properties of propagation channels are used for the design, testing, and type approval of wireless systems [38]. For comparing different MIMO systems and their relevant PHY layer performance enhancement techniques in a manner that is unified and agreed on by many system parties, various organizations introduce the reference channel models with reproducible conditions [38]. Among these modeling methods utilized in site-specific and generic channel model applications (i.e. stored CIR, deterministic channel models, and also stochastic system channel models), the latter one is then selected which describes the predicted probability density function (PDF) of the CIR over a large area. In this research, stochastic modeling of the received radio signal’s amplitude is described by Rayleigh distribution which is used model for predicting PDF of the CIR; in the urban areas with blocked line-of-sight (LoS). Meanwhile, the COST207 models proposed bivariate Gaussian Doppler spectrum for modeling long echoes in urban propagation environments (models in the urban areas) [38]; given by:
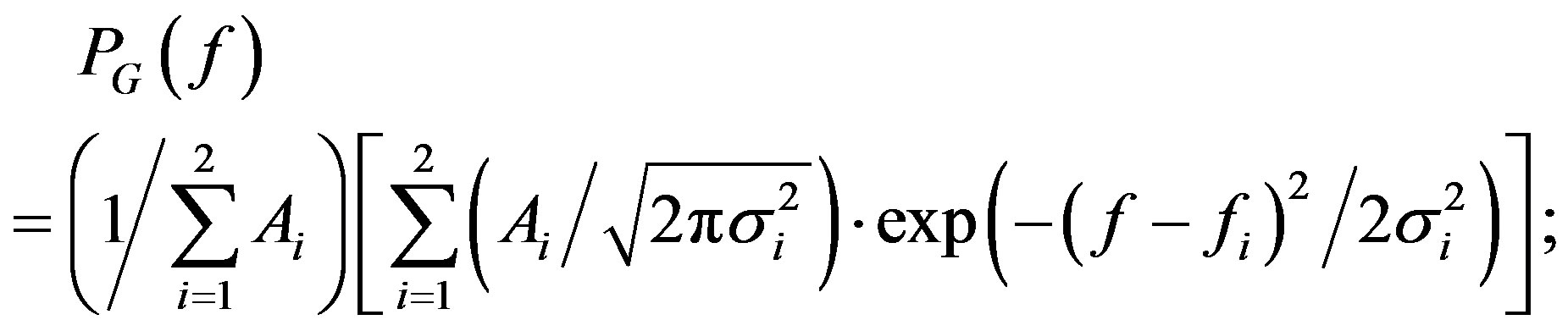
where fi, Ai, and σi, are center frequencies, power gains, and standard deviations respectively [35,39,40].
7. Terrestrial TDE Modeling and Analysis
In the case of complex and real amplitude error functions and in practice, the samples of the received and transmitted signals are existed for the time interval 0 ˂ t ˂ T. The received terrestrial waveform can be modeled as (8):
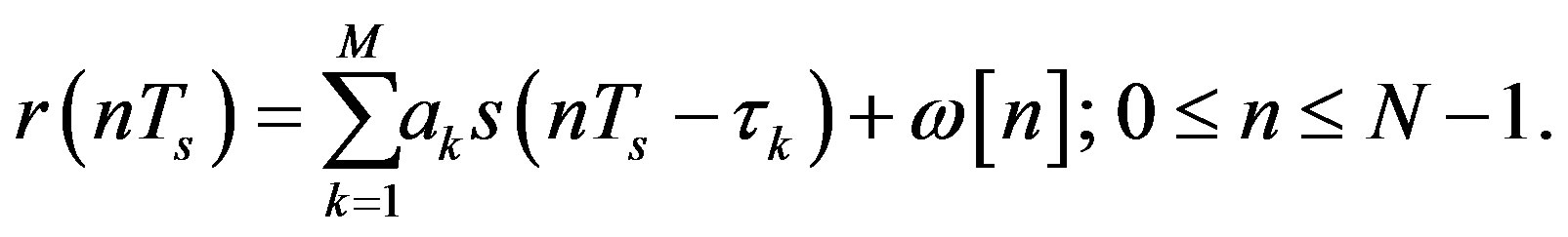 (8)
(8)
where the sampling interval Ts = T/N and ω[n]s are the noise samples of the AWGN with the terrestrial wireless system continuous autocorrelation as (9):
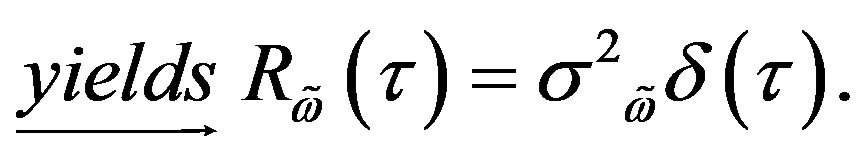 (9)
(9)
where it is assumed that 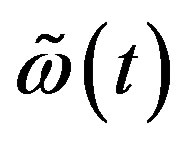 is low-pass filtered (LPF) by the factor as in the Equation (10) below, in order to yield
is low-pass filtered (LPF) by the factor as in the Equation (10) below, in order to yield 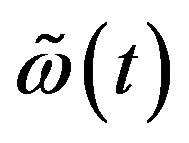 such that the discrete system radio signal has a flat power spectrum as (11).
such that the discrete system radio signal has a flat power spectrum as (11).
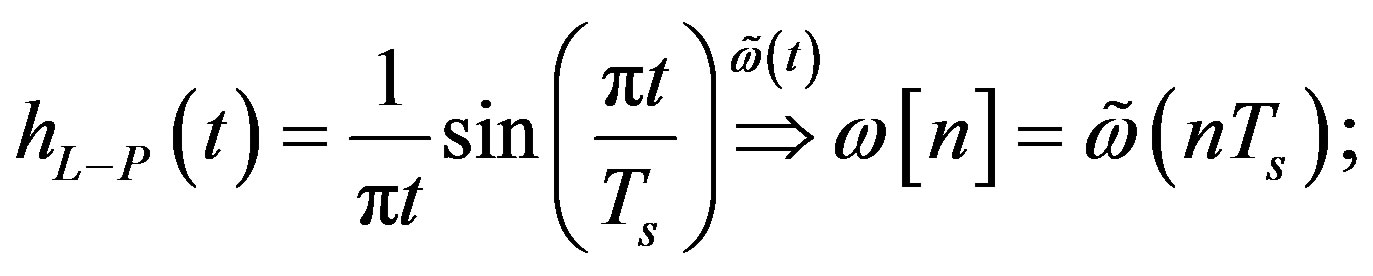 (10)
(10)
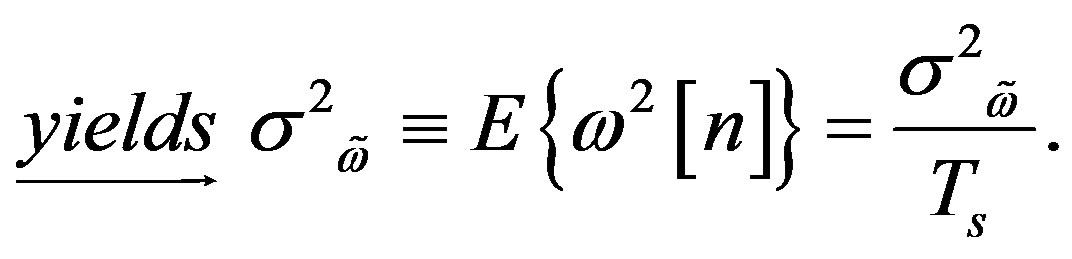 (11)
(11)
The least squares estimator (LSE) of a = [a1, a2,∙∙∙, aM]T and τ = [τ1, τ2,∙∙∙, τM]T has then been obtained by minimizing the squared error function (12) as part of the system time-delay estimation (TDE) computation.
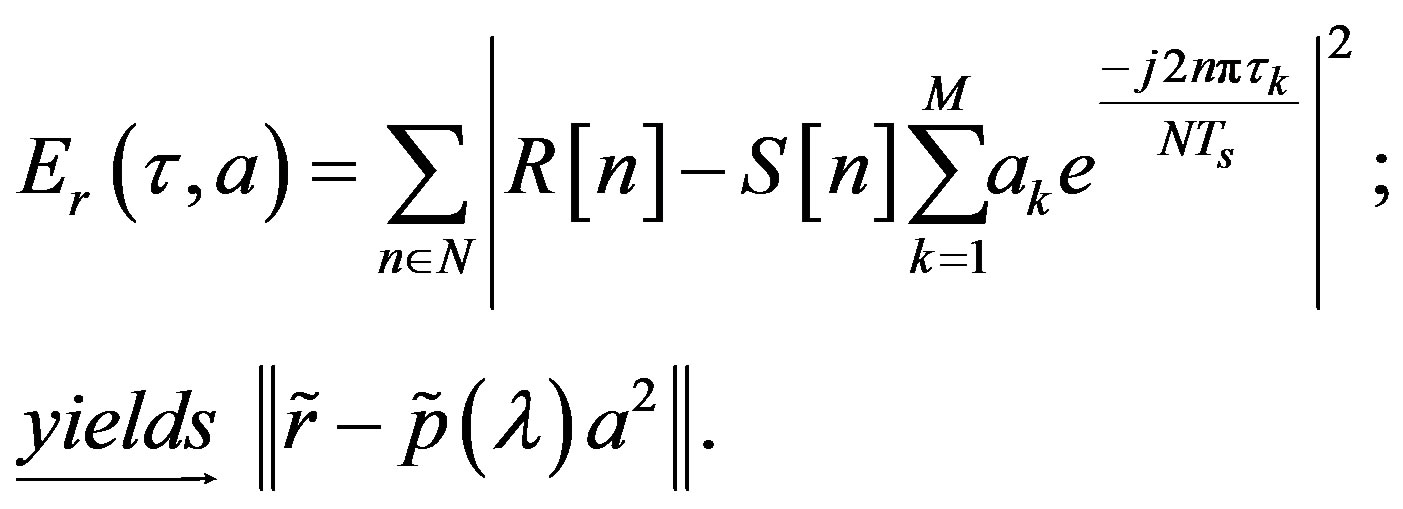 (12)
(12)
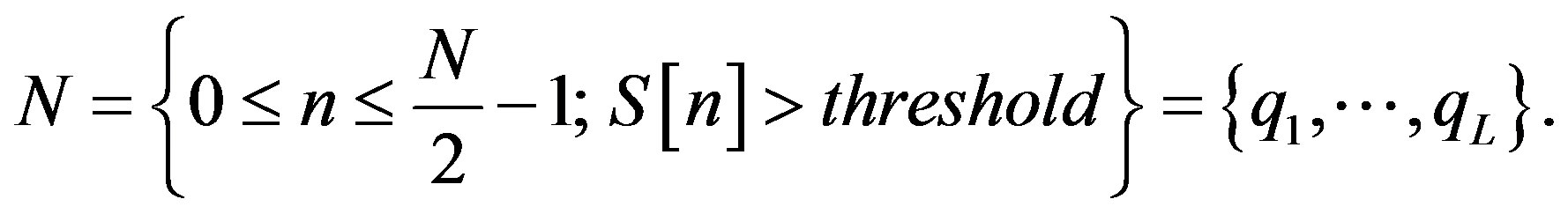 (13)
(13)
where R[n] and S[n] are the discrete Fourier transforms (DFTs) of r[nTs] and s[nTs], respectively. In the presence of AWGN, the LSE is also the maximum likelihood estimator (MLE). In the minimization procedure, a threshold is specified in order to employ only the spectrum regions with the satisfactory system SNRs. The weighting function is employed in order to enhance the accuracy of the estimated delay by attenuating the radiowaves fed into the correlator in spectral region where the SNR is the lowest. For the uncorrelated Gaussian radio system signal, noise, and single path, TDE is asymptotically unbiased and efficient in terms of the limit of long observation intervals. The terrestrial weights the cross-spectral phase according to the estimated phase when variance of the estimated phase error is the least. The system TDE procedure adapts the filter in order to insert a delay equal and opposite to that existing between the two radio signals. In the case of the AWGN presence, the filter weight corresponding to true-delay obtains its maximum value compared to the other TDE terrestrial wireless system filter weights.
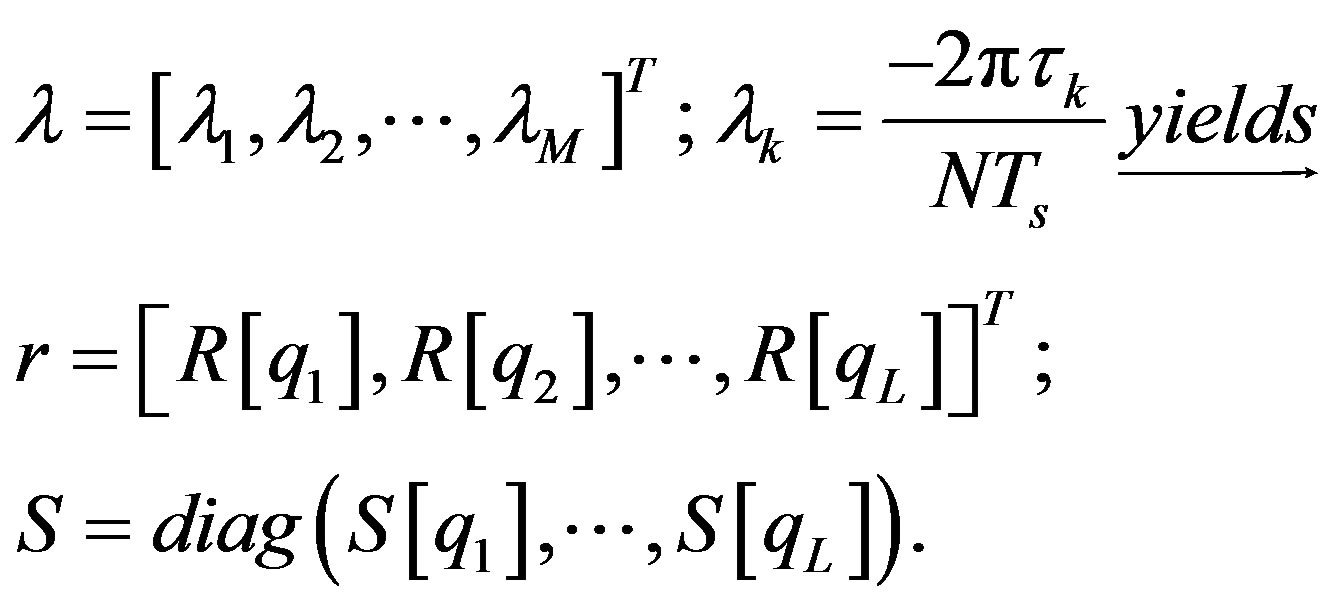 (14)
(14)
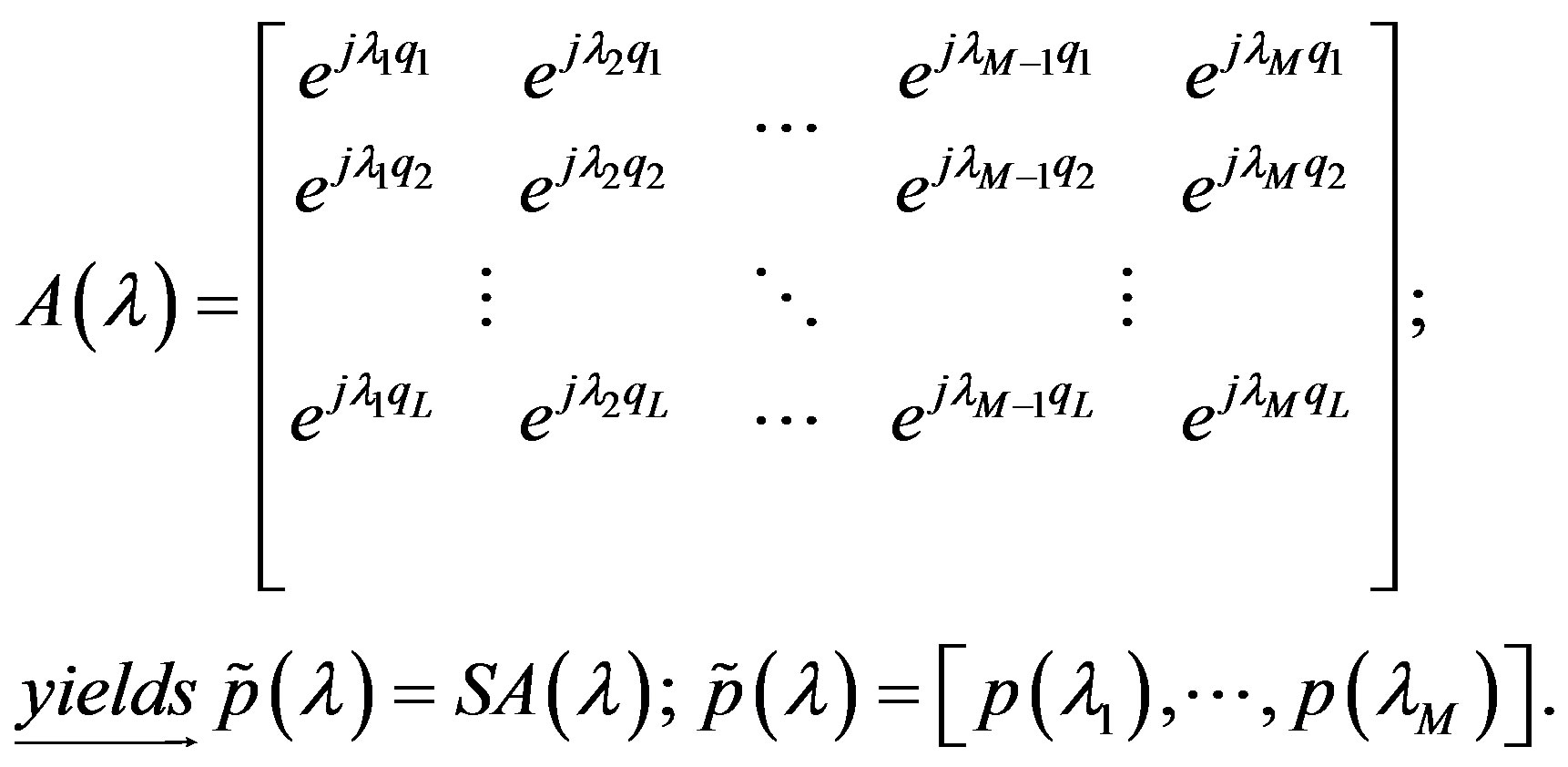 (15)
(15)
where in the relation (14), S[qk] and R[qk] are the timedelay samples that lie above the specified terrestrial wireless system time-delay estimation threshold.
 (16)
(16)
where in the relation (16), the qis are orthogonal, and each one is a function of (λ1, λ2,∙∙∙, λi). Hence Er(λ) can be written as Equation (17) below, in order to minimize the error function for the terrestrial radio signal time-delays.
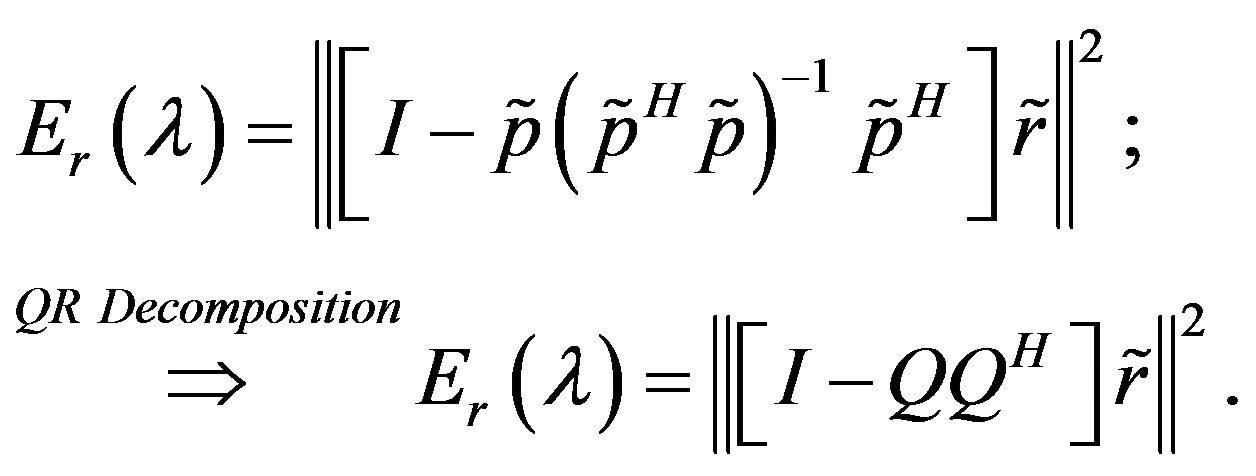 (17)
(17)
8. Terrestrial Communication Results
In this section the simulations are presented which depict the performance (BER) of the terrestrial wireless system. For these simulations, a rate 1/3 SCC has been employed, and formed by the unpunctured recursive convolutional component codes with the polynomial matrices for outer and inner codes. The re-ordering of the outer code’s output is performed based on the algorithm presented in [30] which shown to provide additional coding gains for the SCCs. In this work, the interleaver size is 4096. For the simulations, the wireless communication system employs 16-ary QAM modulation with gray coded bit mapping, and it is assumed that the additive noise at the receiver is AWGN. Figure 2 presents the performance for the discussed wireless system of interest with two transmitter and one receiver antennas (i.e. diversity order DO = 2 × 1
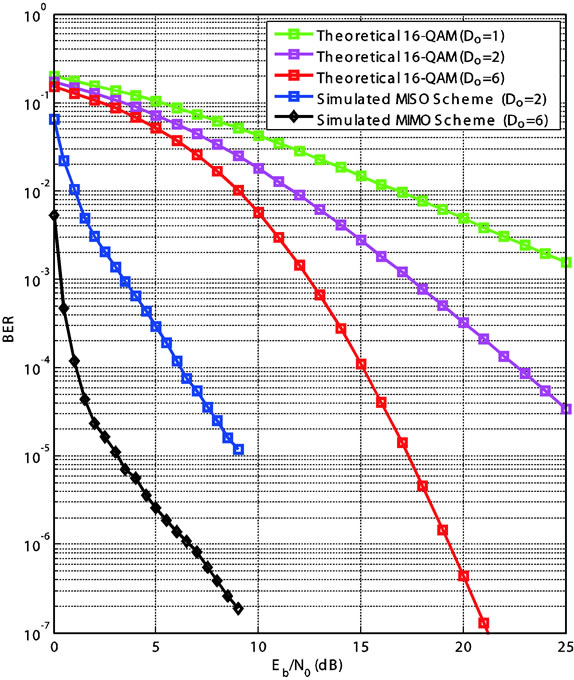
Figure 2. Comparison of BER vs. (Eb/N0) for coded 16-ary QAM MISO (2-Tx, 1-Rx) and MIMO (3-Tx, 2-Rx) terrestrial communication systems.
= 2); and the system results have been compared with the BER curves associated with the theoretical system performance of the uncoded 16-QAM modulation in the Rayleigh multipath channel with DO = 1 (i.e. SISO without diversity), and DO = 2. The figure presents a good terrestrial system reference for comparison since in both approaches, the channel is assumed to be highly faded with blocked LoS. Hence, the additional coding of more than 15 dB implies that the employed technique yields astonishing additional coding gains at the expense of the tolerable system decoding complexities. Meanwhile, it should also be noted that the slope of the BER curve could be simply increased by increasing the component code’s constraint length, the number of decoding iterations, and the interleaver size, at the expense of the delays which might not be acceptable for the hard real-time systems. In addition one more antenna at the transmitter and receiver has been employed in order to evaluate the coding gains due to the deployment of an additional antenna, while relaxing the other system simulation parameters for the designed SCC. In this system Tarokh scheme STBCs have been utilized (DO = 3 × 2 = 6), and compared with theoretical uncoded 16-QAM system over the Rayleigh faded channel with DO = 6. As it can be seen from the figure, while the former scheme results in the BER of 10−5 at SNR = 9 dB, the latter yields the BER of 10−7, which should be considered as an immense terrestrial system advancement. Meanwhile, the introduced enhancement strategy to the wireless system is confirmed from the scatter diagrams (i.e. Figure 3) of the received constellation shapes which have shown that although the received symbols are highly faded for low the SNRs, they land at almost the same locations as in the transmitted constellations (these symbols are transmitted on ±1 + ±j, ±1 + ±3j, ±3 + ±3j and ±3j + ±1j). Figures 4 and 5 present cross-correlation with sharp peak at the correct terrestrial time-delay with the time-lag corresponding to the minimum error as the actual time-delay, and the proposed relation between the SNR and the estimated timedelay in terrestrial environment, respectively.

Figure 3. Comparison of constellations at the MISO and MIMO wireless terrestrial communications receivers for M = 16-ary QAM digital system modulation scheme with gray coded bit assignment.
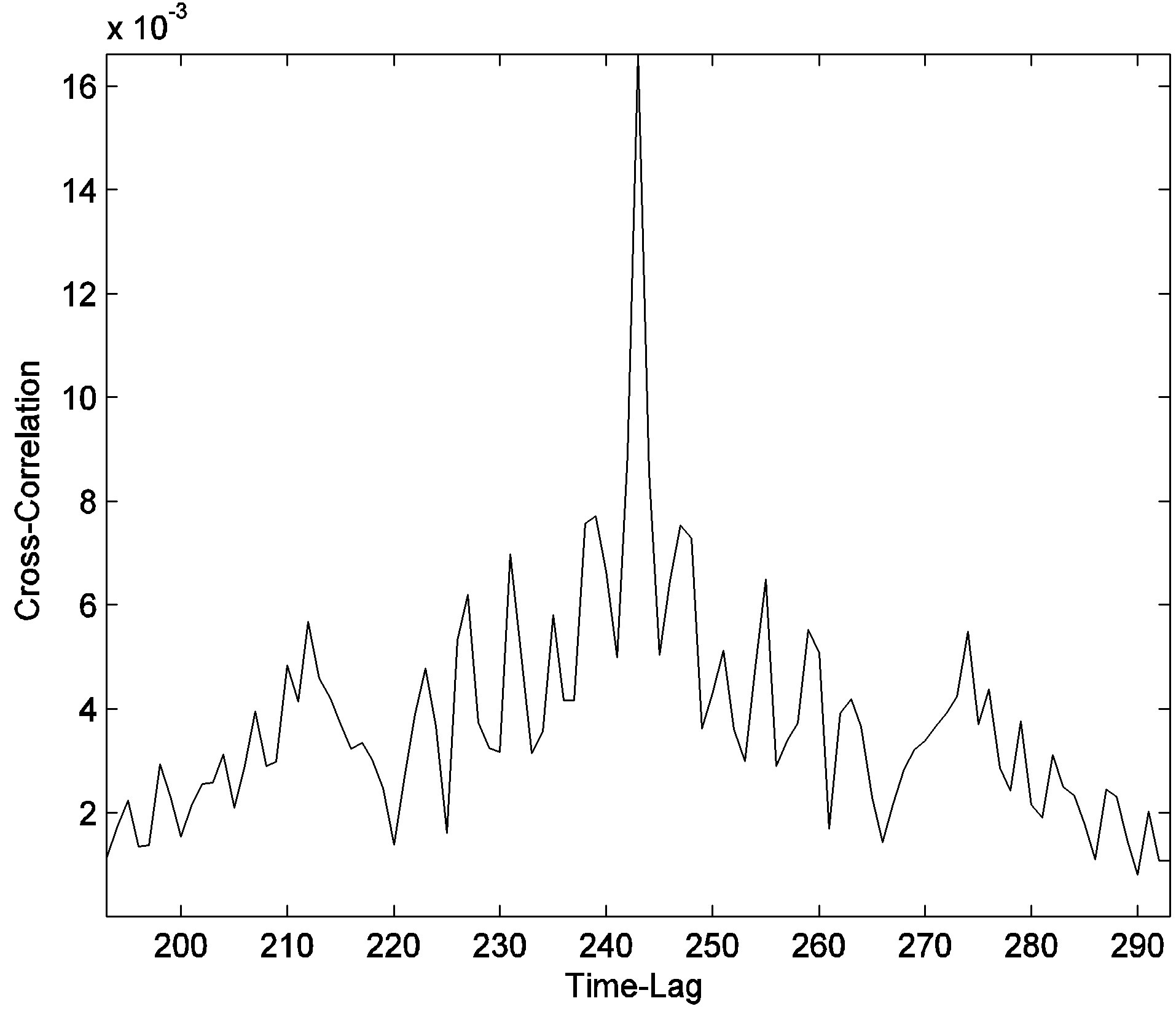
Figure 4. Cross-correlation based on MLE in a simulated multipath terrestrial communications environment in presence of AWGN.
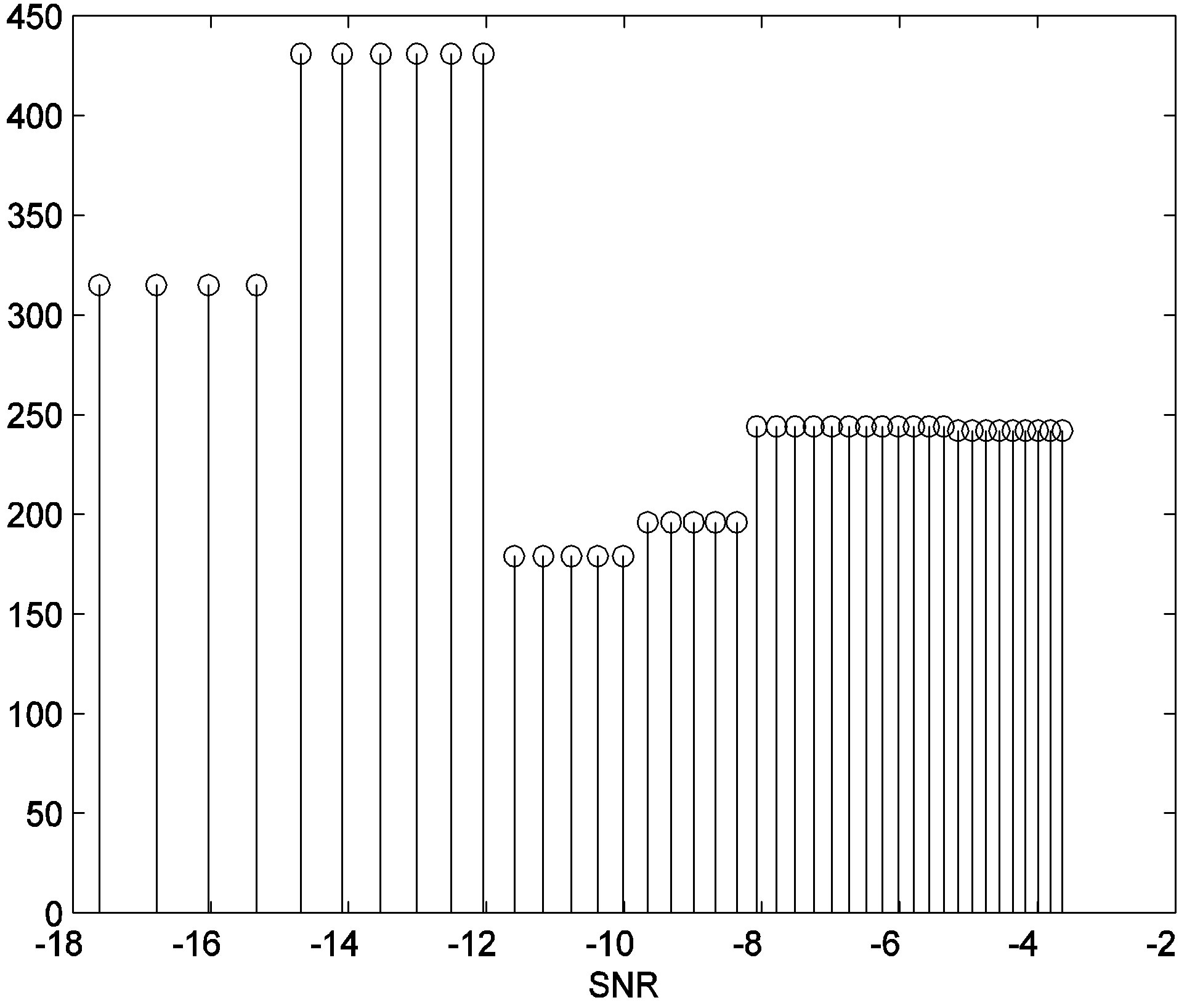
Figure 5. The relation between SNR and estimated timedelays using MLE in a simulated multipath terrestrial communications system environment in presence of AWGN.
9. Concluding Remarks
In this contribution, the performances of space-time codes based on Alamouti and Tarokh STBCs have been thoroughly evaluated in conjunction with high-performance turbo coding system schemes which were previously developed in order to yield astonishing system coding gains.
The introduced technique in this research could also be considered as a potential promising candidate for futuristic terrestrial systems and applications; wherein the channel environment is highly faded, and power and bandwidth are at premium so very low and high-modulation orders may not be adopted for the common highly-faded conditions of the terrestrial propagation environments.
As for the future research, efforts will be put into considering the proposed technique combined with the TCM for improving the system’s efficiency. In this contribution, a promising mathematically-oriented analytical evaluation for the terrestrial system time-delay estimation (TDE) in presence of AWGN in the multipath environment has also been carried out. The presented analytical model can further be extended in order to analyze the terrestrial wireless communication system overall performance for the unknown number of radio paths in specified environment.
REFERENCES
- S. M. Alamouti, “A Simple Transmit Diversity Technique for Wireless Communications,” IEEE Journal on Selected Areas in Communications, Vol. 16, No. 8, 1998, pp. 1451-1458. http://dx.doi.org/10.1109/49.730453
- V. Tarokh, H. Jafarkhani and A. R. Calderbank, “SpaceTime Block Codes from Orthogonal Designs,” IEEE Transactions on Information Theory, Vol. 45, 1999, pp. 1456-1467. http://dx.doi.org/10.1109/18.771146
- V. Tarokh, H. Jafarkhani and A. R. Calderbank, “SpaceTime Block Coding for Wireless Communications: Performance Results,” IEEE Journal on Selected Areas in Communications, Vol. 17, No. 3, 1999, pp. 451-460. http://dx.doi.org/10.1109/49.753730
- T. H. Liew and L. Hanzo, “Space-Time Codes and Concatenated Channel Codes for Wireless Communications,” Proceedings of the IEEE, Vol. 90, No. 2, 2002, pp. 187- 219. http://dx.doi.org/10.1109/5.989869
- X. Zhou, X. Quan and R. Li, “A Dual-Broadband MIMO Antenna System for GSM/UMTS/LTE and WLAN Handset,” IEEE Antennas and Wireless Propagation Letters, Vol. 11, 2012, pp. 551-554. http://dx.doi.org/10.1109/LAWP.2012.2199459
- W. Jaafar, W. Ajib and S. Tabbane, “The Capacity of MIMO-Based Wireless Mesh Networks,” Proceedings of International Conference on Neural Networks (ICON 2007), Adelaide, 19-21 November 2007, pp. 259-264. http://dx.doi.org/10.1109/ICON.2007.4444096
- Q. Li, X. Lin, and J. Zhang, and W. Roh, “Advancement of MIMO Technology in WiMAX: From IEEE 802. 16d/e/j to 802.16m,” IEEE Communications Magazine, Vol. 47, No. 6, 2009, pp. 100-107. http://dx.doi.org/10.1109/MCOM.2009.5116806
- R. Langwieser, C. Angerer and A. L. Scholts, “A UHF Frontend for MIMO Applications in RFID,” 2010 IEEE Radio and Wireless Symposium (RWS), New Orleans, 10-14 January 2010, pp. 124-127. http://dx.doi.org/10.1109/RWS.2010.5434118
- C. Berrou, A. Glavieux and P. Thitimajshima, “Near Shannon Limit Error-Correcting Coding: Turbo Codes,” Proceedings of IEEE International Conference on Communications, 1993, pp. 1064-1070.
- D. Zhao, L. Yue and J. Yang, “Application of Turbo Codes in High-Speed Real-Time Channel,” Journal of Electronics (China), Vol. 23, No. 4, 2006, pp. 602-605. http://dx.doi.org/10.1007/s11767-005-0196-5
- ETSI, “Digital Video Broadcasting (DVB). Interaction Channel for Satellite Distribution Systems,” DVB-RCS 001, 2000.
- 3rd Generation Partnership Project (3GPP), “Multiplexing and Channel Coding (FDD),” 3G TS 25.212, 1999.
- J. Zyren, “Overview of the 3GPP Long Term Evolution Physical Layer,” Freescale Semiconductor Technical Report, 2007.
- A. Ebrahimi and A. Rahimian, “Estimation of Channel Parameters in a Multipath Environment via Optimizing Highly Oscillatory Error Functions Using a Genetic Algorithm,” 15th International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split-Dubrovnik, 15-17 September 2007, pp. 1-5. http://dx.doi.org/10.1109/SOFTCOM.2007.4446112
- P. P. Moghaddam, H. Amindavar and R. L. Kirlin, “A New Time-Delay Estimation in Multipath,” IEEE Transactions on Signal Processing, Vol. 51, No. 5, 2003, pp. 1129-1142. http://dx.doi.org/10.1109/TSP.2003.810290
- H. Amindavar and A. M. Reza, “A New Simultaneous Estimation of Directions of Arrival and Channel Parameters in a Multipath Environment,” IEEE Transactions on Signal Processing, Vol. 53, No. 2, 2005, pp. 471-483. http://dx.doi.org/10.1109/TSP.2004.840673
- H. C. So, “Analysis of an Adaptive Algorithm for Unbiased Multipath Time Delay Estimation,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 39, No. 3, 2003, pp. 777-785. http://dx.doi.org/10.1109/TAES.2003.1238735
- M. M. Kamruzzaman and Li Hao, “Performance of Turbo-SISO, Turbo-SIMO, Turbo-MISO and TurboMIMO System Using STBC,” Journal of Communications—Academy Publisher, Vol. 6, No. 8, 2011, pp. 633- 639.
- A. Hjorungnes and D. Gesbert, “Precoded Orthogonal Space-Time Block Codes over Correlated Ricean MIMO Channels,” IEEE Transactions on Signal Processing, Vol. 55, No. 2, 2007, pp. 779-783. http://dx.doi.org/10.1109/TSP.2006.885760
- F. Jiang, E. Psota and L. C. Perez, “Decoding Turbo Codes Based on Their Parity-Check Matrices,” Proceedings of 39th Southeastern Symposium on System Theory, 2007, pp. 221-224.
- J. Y. Kim and H. V. Poor, “Turbo-Coded Optical DirectDetection CDMA System with PPM Modulation,” Journal of Lightwave Technology, Vol. 19, No. 3, 2001, pp. 312-323. http://dx.doi.org/10.1109/50.918882
- L. Bahl, J. Cocke, F. Jelinek and J. Raviv, “Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate,” IEEE Transactions on Information Theory, Vol. 20, No. 2, 1974, pp. 284-287. http://dx.doi.org/10.1109/TIT.1974.1055186
- W. Koch and A. Baier, “Optimum and Sub-Optimum Detection of Coded Data Distributed by Time-Varying Intersymbol Interference,” Proceeings of IEEE GLOBECOM, Vol. 3, 1990, pp. 1679-1684.
- P. Robertson, E. Villebrun and P. Hoeher, “A Comparison of Optimal and Sub-Optimal MAP Decoding Algorithms Operating in the Log Domain,” Proceedings of IEEE International Conference on Communications (ICC), Vol. 2, 1995, pp. 1009-1013.
- J. Erfanian, S. Pasupathy and P. G. Gulak, “Reduced Complexity Symbol Detectors with Parallel Structure for ISI Channels,” IEEE Transactions on Communications, Vol. 42, No. 234, 1994, pp. 1661-1671.
- S. Benedetto and G. Montorsi, “Serial Concatenation of Block and Convolutional Codes,” Electronics Letters, Vol. 32, No. 10, 1996, pp. 887-888. http://dx.doi.org/10.1049/el:19960621
- S. Benedetto, D. Divsalar, G. Montorsi and F. Pollara, “Serial Concatenation of Interleaved Codes: Performance Analysis, Design, and Iterative Decoding,” The Telecommunications and Data Acquisition Progress Report, Jet Propulsion Lab, 1996, pp. 1-26,
- F. Mehran, “Interleaver Choice in Serially Concatenated Codes for Soft Real-Time Wireless Speech Transmission Applications,” Proceedings of 19th Iranian Conference on Electrical Engineering (ICEE), Tehran, 17-19 May 2011, pp. 1-6.
- O. Y. Takeshita and D. Costello, “New Classes of Algebraic Interleavers for Turbo-Codes,” IEEE International Symposium on Information Theory (ISIT), Cambridge, 16-21 August 1998.
- F. Mehran and A. Rahimian “Physical Layer Performance Enhancement for Femtocell SISO/MISO Soft Real-Time Wireless Communication Systems Employing Serial Concatenation of Quadratic Interleaved Codes,” Proceedings of 20th Iranian Conference on Electrical Engineering (ICEE), May 2012, pp. 1188-1193,. http://dx.doi.org/10.1109/IranianCEE.2012.6292535
- O. Y. Takeshita and D. J. Costello, “New Deterministic Interleaver Designs for Turbo Codes,” IEEE Transactions on Information Theory, Vol. 46, No. 6, 2000, pp. 1988- 2006. http://dx.doi.org/10.1109/18.868474
- H.-Q. Lai and K. J. R. Liu, “Space-Time Network Coding,” IEEE Transactions on Signal Processing, Vol. 59, No. 4, 2011, pp. 1706-1718. http://dx.doi.org/10.1109/TSP.2010.2103063
- E. Telatar, “Capacity of Multi-Antenna Gaussian Channels,” European Transactions on Telecommunications, Vol. 10, No. 6, 1999, pp. 585-595. http://dx.doi.org/10.1002/ett.4460100604
- G. J. Foschini and M. J. Gans, “On Limits of Wireless Communications in a Fading Environment When Using Multiple Antennas,” Wireless Personal Communications., Vol. 6, No. 2, 1998, pp. 311-335. http://dx.doi.org/10.1023/A:1008889222784
- A. Rahimian and F. Mehran, “RF Link Budget Analysis in Urban Propagation Microcell Environment for Mobile Radio Communication Systems Link Planning,” Proceedings of International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, 9-11 November 2011, pp. 1-5. http://dx.doi.org/10.1109/WCSP.2011.6096799
- A. Rahimian and F. Mehran, “BEP Enhancement for Semi-Femtocell MIMO Systems Employing SC-QICs and OSTBCs,” International Journal of Electronics Communication and Computer Technology (IJECCT), Vol. 3, No. 1, 2013, pp. 329-332.
- D. Tse and P. Viswanath, Fundamentals of Wireless Communication, Cambridge University Press, Cambridge, 2005.
- A. F. Molisch, Wireless Communications, 2nd Edition, John Wiley & Sons Ltd., Wiley-IEEE Press, New York, 2011.
- P. Almers, et al., “Survey of Channel and Radio Propagation Models for Wireless MIMO Systems,” EURASIP Journal on Wireless Communications and Networking, 2007.
- J.-M. Conrat and P. Pajusco, “Directional Propagation Channel Estimation and Analysis in Urban Environment with Panoramic Photography,” International Journal of Microwave and Wireless Technologies, Vol. 4, No. 1, 2012, pp. 3-13. http://dx.doi.org/10.1017/S1759078711001139

