Journal of Applied Mathematics and Physics
Vol.06 No.10(2018), Article ID:87729,9 pages
10.4236/jamp.2018.610169
Is ?A−1 an Infinitesimal Generator?
Ru Liu
College of Information Science and Engineering, Chengdu University, Chengdu, China

Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 12, 2018; Accepted: October 7, 2018; Published: October 10, 2018
ABSTRACT
There are some researchers considering the problem whether 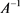 is the generator of a bounded C0-semigroup if A generates a bounded C0-semigroup. Actually, it is a very basic and important problem. In this paper, we discuss whether
is the generator of a bounded C0-semigroup if A generates a bounded C0-semigroup. Actually, it is a very basic and important problem. In this paper, we discuss whether 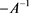 is the generator of a bounded α-times resolvent family if
is the generator of a bounded α-times resolvent family if  generates a bounded α-times resolvent family.
generates a bounded α-times resolvent family.
Keywords:
α-Times Resolvent Family, Analytic α-Times Resolvent Family, Fractional Power of Generator

1. Introduction
In paper [1] , the author studies the problem whether 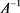 is the generator of a bounded C0-semigroup if A generates a bounded C0-semigroup. We know that α-times resolvent operator family is generalization of C0-semigroup and C0-semigroup is 1-times resolvent operator family. So, in this paper, we will show that when the operator
is the generator of a bounded C0-semigroup if A generates a bounded C0-semigroup. We know that α-times resolvent operator family is generalization of C0-semigroup and C0-semigroup is 1-times resolvent operator family. So, in this paper, we will show that when the operator 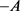 generates a bounded α-times resolvent operator family, under certain condition,
generates a bounded α-times resolvent operator family, under certain condition, 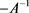 is also the generator of a bounded α-times resolvent operator family. The representation of such bounded α-times resolvent operator family will be obtained, too. Furthermore, we will consider the problem whether
is also the generator of a bounded α-times resolvent operator family. The representation of such bounded α-times resolvent operator family will be obtained, too. Furthermore, we will consider the problem whether 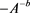 owns this property.
owns this property.
Let us first recall the definitions of α-times resolvent operator family. Let A be a closed densely defined linear operator on a Banach space X and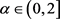 .
.  is a Mittag-Leffler function.
is a Mittag-Leffler function.
Definition 1.1 [2] A family 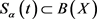 is called an α-times resolvent operator family for A if the following conditions are satisfied:
is called an α-times resolvent operator family for A if the following conditions are satisfied:
1) 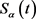 is strongly continuous for
is strongly continuous for 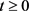 and
and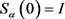 ;
;
2) 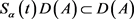 and
and 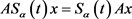 for
for  and
and  ;
;
3) For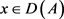 ,
, 
where

If 



Definition 1.2 [2] An α-times resolvent family 









Then we give a Lemma which will be used later.
Lemma 1.1 [2] 




2. Main Theorem and Conclusion
Theorem 2.1. On a Hilbert space H, the following statements are equivalent:
(1)

(2) A is a closed, densely defined operator, 


(3) A is a closed, densely defined operator, for



Proof. (2) Þ (3) For



hence we know 



(3) Þ (2) Since










(1) Þ (2) From lemma 1.3 of [4] , we know that A is a closed, densely defined operator. And we can get the other conclusion from theorem 2.8 of [2] .
(2) Þ (1). Firstly, set




For




Since 






From Lemma II, 3.4(ii) of [5] , we have that 


(a) 

(b) 
(c)
(a) For 


where 



By Lemma II, 3.4(ii) of [5] , 



(b) I. For








II. For





We have




III. We know that
And for


For all the above, we can obtain that 
(c) For each





To sum up the above (a), (b) and (c), we can conclude that
Theorem 2.2.




Proof. In the proof of the previous theorem, we have only used the properties of Hilbert space in the acquisition of 

In fact, on a Banach space, for each


From the subordination principle, we have

We can obtain that this theorem is tenable from the proof of the previous theorem.
Theorem 2.3. On a Hilbert space H, if



Proof. From the above Theorem 2.1, we have











Theorem 2.4. If






where 


Proof. Since





Thus, the integral is well defined. Set 




Consequently, we can obtain a conclusion that 



Theorem 2.5. A satisfies the assumption of Theorem 2.4, for



where
and
is oriented counterclockwise, where
and
Proof.







Since
From [8] , we have that there exists an


The same estimate holds for the integral on
The same estimate holds for the integral on
To sum up, we can conclude that there exists an

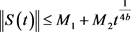

For
From all the above, we can obtain a conclusion that if


3. Conclusion
In this paper, we considered when the operator 



Acknowledgements
The author was supported by Scientific Research Starting Foundation of Chengdu University, No. 2081915055.
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
Cite this paper
Liu, R. (2018) Is ?A−1 an Infinitesimal Generator? Journal of Applied Mathematics and Physics, 6, 1979-1987. https://doi.org/10.4236/jamp.2018.610169
References
- 1. Zwart, H. (2007) Is A-1 an Infinitesimal Generator? Banach Center Publications, 75, 303-313. https://doi.org/10.4064/bc75-0-18
- 2. Bajlekova, E. (2001) Fractional Evolution Equations in Banach Spaces. Ph.D. Thesis, Eindhoven University of Technology.
- 3. Jiang, Z.J. and Sun, S.L. (2005) Functional Analysis. 2nd Edition, Higher Education Press, Beijing. (In Chinese)
- 4. Liu, R., Li, M., Pastor, J. and Piskarev, S. (2014) On the Approximation of Fractional Resolution Families. Differential Equations, 50, 927-937. https://doi.org/10.1134/S0012266114070088
- 5. Engel, K.J. and Nagel, R. (2000) One-Parameter Semigroups for Linear Evolution Equations. Springer, Berlin.
- 6. Erdelyi, A., et al. (1955) Higher Transcendental Functions. McGraw-Hill, New-York.
- 7. Li, M., Chen, C. and Li, F.-B. (2010) On Fractional Powers of Generators of Fractional Resolvent Families. Journal of Functional Analysis, 259, 2702-2726. https://doi.org/10.1016/j.jfa.2010.07.007
- 8. Chen, C., Li, M. and Li, F.-B. (2011) On Bounded Values of Fractional Resolvent Families. Journal of Mathematical Analysis and Applications, 384, 453-467. https://doi.org/10.1016/j.jmaa.2011.05.074




























