Journal of Applied Mathematics and Physics
Vol.06 No.08(2018), Article ID:86630,10 pages
10.4236/jamp.2018.68141
An Optimal Parallel Algorithm for Constructing a Spanning Tree on Proper Circle Trapezoid Graphs
Hirotoshi Honma, Yoko Nakajima, Shino Nagasaki, Atsushi Sasaki
National Institute of Technology, Kushiro College, Kushiro, Japan

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 4, 2018; Accepted: August 11, 2018; Published: August 14, 2018
ABSTRACT
Given a simple graph G with n vertices and m edges, the spanning tree problem is to find a spanning tree for a given graph G. This problem has many applications, such as electric power systems, computer network design and circuit analysis. For a simple graph, the spanning tree problem can be solved in time with processors on the CRCW PRAM. In general, it is known that more efficient parallel algorithms can be developed by restricting classes of graphs. In this paper, we shall propose a parallel algorithm which runs time with processors on the EREW PRAM for constructing on proper circle trapezoid graphs.
Keywords:
Design and Analysis of Parallel Algorithms, Proper Circle Trapezoid Graphs, Spanning Tree

1. Introduction
Given a simple connected graph G with n vertices, the spanning tree problem is to find a tree that connects all the vertices of G. The spanning tree problem has applications, such as electric power systems, computer network design and circuit analysis [1] . A spanning tree can be found in time using, for example, the depth-first search or breadth-first search. In recent years, a large number of studies have been made to parallelize known sequential algorithms. For simple graphs, Chin et al. presented that the spanning forest can be found in time using processors [2] . Moreover, for a connected graph, Klein and Stein demonstrated that a spanning tree can be found in time with processors on the CRCW (Concurrent Read Concurrent Write) PRAM (Parallel Random Access Machine) [3] .
In general, it is known that more efficient algorithms can be developed by restricting classes of graphs. For instance, Wang et al. proposed an optimal parallel algorithm for constructing a spanning tree on permutation graphs that run in time using processors on the EREW (Exclusive Read Exclusive Write) PRAM [4] . Wang et al. proposed optimal parallel algorithms for some problems including the spanning tree problem on interval graphs that can be executed in time with processors on the EREW PRAM [5] . Bera et al. presented an optimal parallel algorithm for finding a spanning tree on trapezoid graphs that take in time using processors on the EREW PRAM [6] . In addition, Honma et al. developed parallel algorithms for finding a spanning tree on circular permutation graphs [7] and circular trapezoid graphs [8] . Both of them take in time using processors on the EREW PRAM.
Felsner et al. first introduced circle trapezoid graphs [9] . They also provided an time algorithm for solving maximum independent set problem and time algorithm for solving maximum clique problem. Recently, Lin showed that circle trapezoid graphs are superclasses of trapezoid graphs [10] .
In this study, we propose a parallel algorithm for spanning tree problem on a proper circle trapezoid graph. It can run in time with processors on the EREW PRAM. The rest of this paper is organized as follows. Section 2 describes some definitions of circle trapezoid graphs and models and introduces the extended circle trapezoid model, as well as some notation. Section 3 presents some properties on circle trapezoid graphs, which are useful for finding a spanning tree in an efficient manner. Section 4 describes our parallel algorithm for the spanning tree problem and its complexity. Finally, Section 5 concludes the paper.
2. Preliminaries
2.1. Circle Trapezoid Model and Graph
We first illustrate the circle trapezoid model before defining the circle trapezoid graph. There is a unit circle C such that the consecutive integer i, are assigned clockwise on the circumference (n is the number of circle trapezoids). Consider nonintersecting two arcs and along the circumference of C. The point (resp., ) is the last point encountered when traversing (resp., ) clockwise. A circle trapezoid is the region in a circle C that lies between two non-crossing chords and . Without loss of generality, each circle trapezoid has four corner points , and all corner points are distinct. We assume that circle trapezoids are labeled in increasing order of their corner points ’s, i.e., if . The geometric representation described above is called the circle trapezoid model. Figure 1(a) illustrates an example of a circle trapezoid model M with eight circle trapezoids. The circle trapezoid with is called feedback circle trapezoid. Note that there exist two feedback circle trapezoids ( ) in a circle trapezoid model M.
An undirected graph G is a circle trapezoid graph if it can be represented by the following circle trapezoid model; each vertex of the graph corresponds to a circle trapezoid in circle trapezoid model, and two vertices are adjacent in G if and only if their circle trapezoids intersect [9] . Figure 1(b) illustrates a circle trapezoid graph G corresponding to M shown in Figure 1(a). Table 1 shows the details of circle trapezoid model M of Figure 1.
2.2. Extended Circle Trapezoid Model
In the following, we introduce the extended circle trapezoid model EM constructed from a circle trapezoid model for making the problem easier. We first cut a circle trapezoid model M at point 1 on the circumference and next unroll onto the real horizontal line. Each circle trapezoid in M is also changed to a pair of line segment called interval pair by executing the above process. Here, feedback circle trapezoid in M is changed to interval pair for . Moreover, copies of are created by shifting 4n to the left respectively, for each , . Note that both interval pairs and in extended circle trapezoid model EM are corresponding to in M.
The following Algorithm CEM constructs an EM from a M. Figure 2 shows the EM constructed from the M illustrated in Figure 1. Table 2 shows the details of EM of Figure 2.
Algorithm CEM
Input: Corner points of in M.
Begin
For each non feedback circle trapezoid pardo
Create a interval pair ;
For each feedback circle trapezoid pardo
For each
Create a interval pair ;
For pardo
Create copies by shifting 4n to the left for ;
End
3. Proper Circle Trapezoid Model and Graph
3.1. Definitions for Proper Circle Trapezoid Graph
In this study, we focus and treat a proper circle trapezoid graph. Graph G is a circle trapezoid graph corresponding to a circle trapezoid model M and an extended circle trapezoid model EM is constructed from M by executing Algorithm CEM. We consider circle trapezoid model M such that the extended
Figure 1. Circle trapezoid model and graph. (a) Circle trapezoid model M; (b) Circle trapezoid graph G.
Figure 2. Extended circle trapezoid model EM.
Table 1. Details of circle trapezoid model M.
Table 2. Details of extended circle trapezoid model EM.
circle trapezoid model EM constructed from M satisfies that for two interval pairs and in EM. The circle trapezoid model is defined as proper circle trapezoid model. The graph corresponding to the proper circle trapezoid model is proper circle trapezoid graph . In this study, we will develop a parallel algorithm for spanning tree problem on proper circle trapezoid graphs. The Figure 1 is also an example of and because for and in extended circle trapezoid model EM.
Here, some notations that form the basis of our algorithm are defined as follows.
The function normalizes the interval pair number i in EM within the range 1 to n, which is expressed as
For the example shown in Figure 2, for and , we have and , respectively.
The function computes a vertex number i satisfying for a given number k on EM. For the example shown in Figure 2, for and , we have and by and , respectively. Moreover, we use instead of for simplicity. For the example shown in Figure 2, for and , we have and by and , respectively.
We next define , for , in . The details of , , and are shown in Table 3.
3.2. Property of Proper Circle Trapezoid Graph
We describe some properties on circle trapezoid graphs which are useful for constructing the algorithm for spanning tree problem on proper circle trapezoid graphs.
For two interval pairs
and
in EM, we say
and
are disjoint if
. Moreover, we say
contain
if 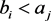 and
and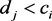 . Figure 3 shows examples of the cases of disjoint and contain. The following Lemma 1 has been described in [9] .
. Figure 3 shows examples of the cases of disjoint and contain. The following Lemma 1 has been described in [9] .
Table 3. Details of extended circle trapezoid model EM.
Figure 3. Examples of disjoint and contain. (a) 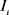 and
and  are disjoint (
are disjoint (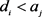 ); (b)
); (b) 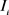 contains
contains 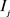 (
(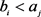 and
and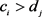 ).
).
Lemma 1 Let 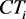 and
and 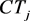
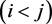 be non-feedback circle trapezoids in circle trapezoid model M. Moreover, extended circle trapezoid model EM is constructed from M.
be non-feedback circle trapezoids in circle trapezoid model M. Moreover, extended circle trapezoid model EM is constructed from M. 





The following Lemma 2 generalizes Lemma 1. This is very useful to find the edges on circle trapezoid graph.
Lemma 2 G is a circle trapezoid graph corresponding to a circle trapezoid model M, and extended circle trapezoid model EM is constructed from M. For two interval pairs 


1)
2) 

(Proof) By Lemma 1, for two non-feedback circle trapezoids 
















For the condition (










We obtain the following Lemma 3 for a proper circle trapezoid model 

Lemma 3. 








(Proof) By Lemma 2, if either of conditions 1) (




















In Lemma 2, we have to test if 







The following Lemma 4 is core of solving this problem. An efficient algorithm can be constructed by using the following lemma.
Lemma 4. 








(Proof) By the definition,









4. Parallel Algorithm
In this section, we propose an algorithm for constructing a spanning tree of a connected proper circle trapezoid graph

Algorithm CST
Input: 


Output: A spanning forest F of G. Initially F be an empty set.
Begin
(Step 1) % Initializing

For i, 

For i, 

(Step 2) % Computing
For i, 


For i, 

For i, 

(Step 3) % Construct a spanning forest
For i, 
If
then
End
Lemma 5. After executing Step 3 of Algorithm CST, graph T is a spanning tree of proper circle trapezoid graph
(Proof) Step 1 is a process for initialization. T is empty set and all 


In Step 2, we set
















We consider that T is added an edge form i to 












Figure 4. Example of constructed spanning tree.
In Step 3, in the case of













Therefore, after executing Step 3 of Algorithm CST, graph T is a spanning tree of proper circle trapezoid graph
Figure 4 shows a spanning tree T constructed from CTG 
In the following, we analyze the complexity of Algorithm CST.
In Step 1, an extended circle trapezoid model is constructed from a circle trapezoid model in 











Theorem 6. Algorithm CST constructs a spanning tree of a proper circle trapezoid graph in 

5. Concluding Remarks
In this paper, we presented a parallel algorithm to solve the spanning tree problem on a proper circle trapezoid graph. This algorithm can be implemented in 

Acknowledgements
We express many thanks to anonymous referees for their valuable advices on the theory of our attacks and their helpful editorial comments. This work was supported by JSPS KAKENHI Grant Number 17K00324 and 17K04965.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Honma, H., Nakajima, Y., Nagasaki, S. and Sasaki, A. (2018) An Optimal Parallel Algorithm for Constructing a Spanning Tree on Proper Circle Trapezoid Graphs. Journal of Applied Mathematics and Physics, 6, 1649-1658. https://doi.org/10.4236/jamp.2018.68141
References
- 1. Wilson, R.J. (1996) Introduction to Graph Theory. Prentice Hall, Upper Saddle River.
- 2. Chin, F.Y., Lam, J. and Chen, I. (1982) Efficient Parallel Algorithms for Some Graph Problems. Communications of the ACM, 25, 659-665. https://doi.org/10.1145/358628.358650
- 3. Klein, P. and Stein, C. (1990) A Parallel Algorithm for Eliminating Cycle in Undirected Graphs. Information Processing Letters, 34, 307-312. https://doi.org/10.1016/0020-0190(90)90015-P
- 4. Wang, Y. L., Chen, H. C. and Lee, C. Y. (1995) An Parallel Algorithm for Constructing a Spanning Tree on Permutation Graphs. Information Processing Letters, 56, 83-87. https://doi.org/10.1016/0020-0190(95)00125-V
- 5. Wang, Y. L., Chiang, K. C. and Yu, M. S. (1998) Optimal Algorithms for Interval Graphs. Journal of Information Science and Engineering, 14, 449-459.
- 6. Bera, D., Pal, M. and Pal, T. K. (2003) An Optimal PRAM Algorithm for a Spanning Tree on Trapezoid Graphs. Journal of Applied Mathematics and Computing, 1-2, 21-29. https://doi.org/10.1007/BF02936178
- 7. Honma, H., Honma, S. and Masuyama, S. (2009) An Optimal Parallel Algorithm for Constructing a Spanning Tree on Circular Permutation Graphs. IEICE Transactions on Information and Systems, E92-D, 141-148. https://doi.org/10.1587/transinf.E92.D.141
- 8. Honma, H., Nakajima, Y., Igarashi, Y. and Masuyama, S. (2014) Algorithm for Finding Maximum Detour Hinge Vertices of Interval Graphs. IEICE Transactions on Fundamentals of Electronics, E97-A, 1365-1369. https://doi.org/10.1587/transfun.E97.A.1365
- 9. Felsner, S., Müller, R. and Wernisch, L. (1997) Trapezoid Graphs and Generalization, Geometry and Algorithms. Discrete Applied Mathematics, 74, 13-32. https://doi.org/10.1016/S0166-218X(96)00013-3
- 10. Lin, W. L. (2006) Circular and Circle Trapezoid Graphs. Journal of Science and Engineering Technology, 2, 11-17.
- 11. Gibbons, A. and Rytter, W. (1988) Efficient Parallel Algorithms. Cambridge University Press, Cambridge.
- 12. Brent, R. P. (1974) The Parallel Evaluation of General Arithmetic Expressions. Journal of the ACM, 21, 201-206. https://doi.org/10.1145/321812.321815








