ABSTRACT

Modifications of the Weyl-Heisenberg algebra 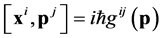are proposed where the classical limit 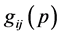corresponds to a metric in (curved) momentum spaces. In the simplest scenario, the 2D de Sitter metric of constant curvature in momentum space furnishes a hierarchy of modified uncertainty relations leading to a minimum value for the position uncertainty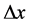. The first uncertainty relation of this hierarchy has the same functional form as the stringy modified uncertainty relation with a Planck scale minimum value for 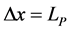at. We pro- ceed with a discussion of the most general curved phase space scenario (cotangent bundle of spacetime) and provide the noncommuting phase space coordinates algebra in terms of the symmetric 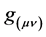and nonsymmetric 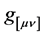metric com- ponents of a Hermitian complex metric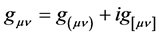, such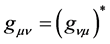. Yang’s noncommuting phase-space coordinates algebra, combined with the Schro- dinger-Robertson inequalities involving angular momentum eigenstates, reveals how a quantized area operator in units of 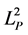emerges like it occurs in Loop Quantum Gravity (LQG). Some final comments are made about Fedosov deformation quanti- zation, Noncommutative and Nonassociative gravity.

Keywords:

Uncertainty Relations, Gravity, Finsler Geometry, Born Reciprocity, Phase Space

Generalized Uncertainty Relations

Recently, we studied the generalized gravitational field equations in curved phase spaces (the cotangent bundle of spacetime) [1] . A nontrivial solution generalizing the Hilbert-Schwarzschild black hole metric in spacetime was found. The most relevant physical consequence is that the metric becomes momentum-dependent (observer dependent) which is what one should aim for in trying to quantize geometry (gravity): The observer must play an important role in any measurement (observation) process of the spacetime he/she lives in.

Most of the work devoted to Quantum Gravity has been focused on the geometry of spacetime rather than phase space per se. The first indication that phase space should play a role in Quantum Gravity was raised by [2] . The principle of Born’s reciprocal relativity [2] was proposed long ago based on the idea that coordinates and momenta should be unified on the same footing, and consequently, if there is a limiting speed (temporal derivative of the position coordinates) in Nature given by the speed of light, there should be a maximal force as well, since force is the temporal derivative of the momentum. An upper bound on the force does not imply that there is a maximum momentum. Likewise, in ordinary Special Relativity, an upper bound (speed of light) on the velocity does not imply that there is a maximum length. To sum up, a direct consequence of the Born reciprocity principle is that a maximal speed limit (speed of light) should be accompanied with a maximal proper force.

It is better understood now that the Planck-scale modifications of the particle dispersion relations can be encoded in the nontrivial geometrical properties of momentum space [3] . When both spacetime curvature and Planck-scale deformations of momentum space are present, it is expected that the nontrivial geometry of momentum space and spacetime get intertwined. The interplay between spacetime curvature and non- trivial momentum space effects was essential in the notion of “relative locality” and in the deepening of the relativity principle [3] . Recently the authors [4] described the Hamilton geometry of the phase space of particles whose motion is characterized by general dispersion relations. Explicit examples of two models for Planck-scale modified dispersion relations, inspired from the q-de Sitter and k-Poincare quantum groups, were considered. In the first case they found the expressions for the momentum and position dependent curvature of spacetime and momentum space, while for the second case the manifold is flat and only the momentum space possesses a nonzero, momentum dependent curvature.

We shall focus in this work on two main points. Firstly, on solutions to the field equations in momentum space with the inclusion of the momentum analog of a cosmologically constant.

(1)

the solutions to the above field equations will be used in the modified uncertainty relations. The momentum-space analog of the cosmological constant should not be confused with the spacetime one.

Secondly, on the rotationally invariant commutator of the form [5]

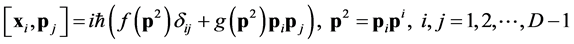(2)

one can see that under rotations

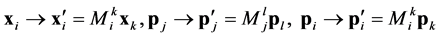(3)

the left and right hand side of Equation (2) become

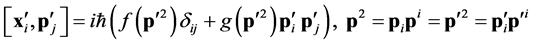(4)

and the commutator relations remain invariant. Consequently, if one is to set

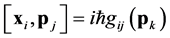, a rotationally invariant commutator can be associated to a classi- cal momentum space metric of the form

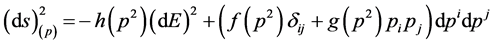(5)

A close inspection reveals that the 4D momentum-space metric analog of the de Sitter metric in a 4D spacetime (written in static coordinates and using the momentum- space analog of the cosmological constant)

(6)

does not have the required form indicated by Equation (5). To verify this one simply rewrites the de Sitter metric in Cartesian coordinates. One then finds that the rota- tionally invariant commutation relations, leading to the metrics (5), are not compatible with a spherically symmetric momentum space de Sitter metric (6).

One may insert the metric (5) into the field equations in momentum space in order to determine whether or not there exist actual functions which solve the field Equation (1). However, for our purposes it is not necessary to do so, and it is much simpler just to write down the momentum space analog of the de Sitter metric in 2D in natural units

(7)

which is trivially rotational invariant. in 2D. There is a cosmological horizon in

momentum space when. We shall choose the length scale

to coincide with the Planck length so that the momentum horizon is the Planck momentum.

Inspired by the 2D de Sitter momentum space metric (7), and by promoting the classical momentum variable to an operator, such that, the Schrodinger-Robertson inequality yields the modified uncertainty relations after performing a series expansion (with)

(8)

One may notice that since for, given a self-adjoint (Her- mitian) momentum operator, one may drop the absolute value symbol in last terms of Equation (8). The (geometric) series expansion in converges as an operator if

(9)

consistent with the cosmological momentum-horizon being an ultraviolet cutoff value for the momentum. The unit operator is and the states are normalized to unity so that.

Inserting the inequality of the equation below

(10)

into Equation (8), yields to leading order in, a modified uncertainty relation

(11)

which has the same functional form as the stringy modified uncertainty relations [6] , with the main difference being that now one has the cosmological momentum-horizon

as an ultraviolet cutoff for, and there is an strict inequality in Equation

(11).

The minimum value for the position uncertainty is at

and which coincides with the location of the cosmological momentum horizon. If one equates the minimum value of the position uncertainty to the Planck scale length it gives, and which is consistent with the fact that we chose the length scale L to coincide with the Planck length.

To sum up, to leading order in L, the de Sitter momentum space metric in 2D

furnishes: 1) a cosmological momentum-horizon as an ultraviolet

cutoff; 2) a Planck scale minimal length uncertainty for the position coordinate

at.

The next-to-leading order term can be obtained after using the inequality

(12a)

that simply follows from

(12b)

after replacing and recurring to. Upon doing so one obtains another modified uncertainty relation given by

(12c)

The minimum position uncertainty now turns out to be at

(12d)

The value of lies between. Repeating the procedure based

on Equation (12a), Equation (12b), by a process of successive squaring, a hierarchy of modified uncertainty relations of the form are derived

(12e)

The most salient feature of the modified uncertainty relations (11), (12c), (12d) is that there is a minimum value for the position uncertainty. The Scale Relativity Theory [7] is based on the postulate that the Planck scale is the minimum length resolution. Generalized uncertainty relations in spacetime were derived from the Extended Relativity Theory in Clifford spaces (C-spaces) in [8] . Such Clifford space Extended Relativity Theory has two universal parameters: the speed of light and the Planck length.

In general one can postulate the following modification of the Weyl-Heisenberg algebra

(13)

combined with the additional commutation relations

(14)

with the provision that the above commutators obey the Jacobi identities [5] . A nonvanishing is compatible with a curved momentum space. The de Sitter momentum space metric yields a constant scalar curvature in momentum space. The vanishing commutator is consistent with a flat spacetime. A nontrivial problem is to find the most general solutions to the field equations in momentum space (with and without the) for the metric which has the form of Equation (5), in order to yield rotationally symmetric commutators, after promoting the classical momentum variables to self-adjoint operators. When the momentum space is still commutative, one can find a Hilbert space representation in the spectral representation of the momentum operator [5] . The states were analyzed in detail by [5] . Upon performing the expectation values one recovers the classical metric in momentum space. These momentum eigenstates have for momentum uncertainty so that, as expected.

The more general commutator than the one in Equation (13)

(15)

may be chosen such that the classical limit (involving c varia- bles) furnishes a classical phase space metric obeying the full-fledged gravitational field equations in curved phase spaces (cotangent bundle of spacetime). This poses more difficulties due to the ordering ambiguities of the operators inside. One can solve this ordering ambiguity by performing a Weyl ordering procedure, like

to ensure that the latter ordering is Hermitian, since the product

is not.

An important remark is in order. By Hermitian metric one usually means. This should not be confused with performing the Hermitian (adjoint) operation to each one of the entries inside the metric matrix. If the entries of the metric matrix are given by polynomials in the operators, the Weyl ordering procedure will ensure that each one of the entries of the metric matrix will remain Hermitian. For

example if, a Weyl ordering yields ensuring that

the argument of the metric matrix is Hermitian. Similarly, by anti-Hermitian metric one usually means.

Since the commutator of two Hermitian operators in anti-Hermitian, one may postulate the following commutators below (in a fully relativistic phase space) given in terms of of a real metric which has both symmetric and anti-symmetric com- ponents as follows ()

(16)

are real numerical coefficients.

(17)

(18)

the right hand sides are anti-Hermitian due to. A Taylor expansion of the metric components in powers of must be followed by a Weyl ordering of all the variables to ensure Hermiticity of the arguments of the metric. An UV (ultra- violet) cutoff is given by the Planck scale; an IR (infrared) cutoff is given by (Hubble radius). The Jacobi identities will impose very strong constraints on the functional form of and. A complex Hermitian metric can be introduced by writing such that. This raises the possibility that complex Hermitian metrics might be relevant in Quantum Gravity.

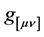
It is at this point where the following Schrodinger-Robertson inequalities for 2n observables will play an important role. They are given by the inequality of the determinants below involving the covariance and commutator matrices [9]

(19)

the covariance is defined as

(20)

uncorrelated variables have zero covariance. The uncertainty squared is

.

For the 2n phase space coordinates, the and matrices are respectively given by

(21)

(22)

Due to the nontrivial commutation relations (16)-(18), the Schrodinger-Robertson inequalities will lead to very complicated uncertainty relations. Further- more, because the phase space coordinates are noncommutative [10] , one must deal now with Noncommutative Quantum Mechanics; i.e. Quantum Mechanics on Non- commutative spacetimes which is the realm of Hopf algebras and Quantum Groups.

Closely related to the nontrivial commutation relations (16)-(18) is Yang’s algebra in an 8D Noncommutative phase space [11]

(23)

(24)

(25)

(26)

(27)

(28)

(29)

Yang’s algebra can be obtained simply by replacing

(30)

and recurring to the angular momentum algebra in 6D. The Jacobi identities are satisfied because the angular momentum algebra in 6D obeys them. The noncommuting coordinates and momenta are just rotations/boosts involving the extra directions. may be chosen to be, depending on the signature of the extra two dimensions. is an exchange operator which exchanges in Equation (28). When and/or,. Thus the classical commuting 8D phase space is recovered when and.

One may notice that Yang’s algebra and the algebra of Eqsuations (16)-(18) bears a certain resemblance if one were to set the numerical coefficient B to zero;

, and. The Schrodinger-Robertson inequalities could be applied directly to the Yang’s algebra commutators by taking the expectation values with respect to angular momentum eigenstates. If one were to interpret as a bivector Hermitian operator, and which in turn can be seen as a geometric area operator, then the norm of the spatial area operator would be

(31)

which bears a similarity to the results associated to the area operator obtained in Loop Quantum Gravity (LQG) and based on spin networks. The Planck area is the quantum of minimal area [12] . This deserves further investigation. Modified uncertainty re- lations also apply to the energy and time variables as well. The granularity of spacetime has been interpreted from the principle of Born reciprocity by [9] .

Symplectic geometry is the realm of phase spaces [13] where the symplectic form plays an essential role. Fedosov deformation quantization [14] and the generalized star products in curved phase spaces are tailor made for these generalized gravitational theories in curved phase spaces (cotangent bundle). The geometry of the cotangent bundle of spacetime has been rigorously studied by [15] , among others. In particular, deformation quantization in Fedosov-Finsler spaces has been analyzed extensively by [16] .

To conclude, we may add that non-geometric fluxes in string theory give rise to noncommutative/nonassociative structures. More recently, the differential geometry on the simplest nonassociative (phase) space arising for a constant non-geometric R-flux has been analyzed in [17] . This nonassociativity for a constant R-flux background in closed strings is captured by the commutation relations

. These studies paves the road towards a Non- commutative and Nonassociative gravity which might be a key feature in the final theory of Quantum Gravity.

Acknowledgements

We thank M. Bowers for very kind assistance.

Cite this paper

Castro, C. (2016) Generalized Uncertainty Relations, Curved Phase-Spaces and Quantum Gravity. Journal of Applied Mathematics and Physics, 4, 1870-1878. http://dx.doi.org/10.4236/jamp.2016.410189

References